全卷积网络FCN详解

入门小菜鸟，希望像做笔记记录自己学的东西，也希望能帮助到同样入门的人，更希望大佬们帮忙纠错啦~侵权立删。

目录

一、FCN提出原因

二、FCN的网络结构分析

三、基本网络结构的源码分析（FCN-32s）

1、conv_relu函数——用于定义卷积层以及该层的激活函数层

2、max_pool函数——用于定义池化层

3、fcn函数——用于生成train.prototxt和val.prototxt

四、FCN跳级结构原理解析

五、FCN跳级结构源码分析

---

一、FCN提出原因

为了解决图像分割这种像素级别的问题。

图像分类是图像级别的，一般使用CNN为基础框架进行分类，但是CNN难以应用于图像分割

原因：

（1）CNN在进行卷积和池化过程中丢失了图像细节，即feature map size渐渐减小，因此不能很好指出物体的具体轮廓，指出每个像素具体属于哪个物体，从而无法做到精确的分割。

（2）一般CNN分类网络都会在最后加入一些全连接层，经过softmax后就可以获得类别概率。但是这个概率是一维的，就是说只能标识整个图片（或整个网格内对象）的类别，不能标识每个像素点的类别，所以全连接方法并不适用于图像分割

因此FCN应运而生

---

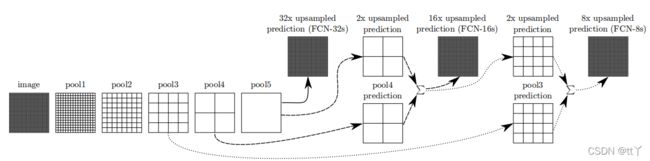
二、FCN的网络结构分析

传统的CNN网络结构如图的上部分，前面5层是卷积层，第6和7层都是长度为4096的一维向量，而第8层是长度为1000的一维向量（代表着1000种类别概率信息）

而FCN将第6，7，8层这些原本是全连接层替换成卷积层，卷积核的大小(通道数，宽，高)分别为（4096,7,7）、（4096,1,1）、（1000,1,1），最后输出的是和输入一样的尺寸，输出尺寸类别种类数+1（背景）

因为这样一来网络里全是卷积层，所以才有这么个名字——全卷积网络

并且FCN的输入可以是任意尺寸图像彩色图像

简单来说，FCN就是将CNN最后的全连接层换成卷积层，输出和输入一样尺寸的已经标好每个像素类别概率值的图

---

三、基本网络结构的源码分析（FCN-32s）

FCN源码地址：

https://github.com/shelhamer/fcn.berkeleyvision.org 

我们以voc-fcn32s/net.py来阐述

1、conv_relu函数——用于定义卷积层以及该层的激活函数层

• bottom：即该层的上一层的输出

• nout：该卷积层输出的数目（即输出的特征图数目）

• ks：卷积核的大小尺寸

• stride：步长

• pad：填充数

其中param的前部分是权重W的学习速率和衰减系数设置；

后部分是偏置b的学习速率（偏置不设置衰减系数）设置

def conv_relu(bottom, nout, ks=3, stride=1, pad=1):
    conv = L.Convolution(bottom, kernel_size=ks, stride=stride,
        num_output=nout, pad=pad,
        param=[dict(lr_mult=1, decay_mult=1), dict(lr_mult=2, decay_mult=0)])
    return conv, L.ReLU(conv, in_place=True)

2、max_pool函数——用于定义池化层

全部采用最大池化法

def max_pool(bottom, ks=2, stride=2):
    return L.Pooling(bottom, pool=P.Pooling.MAX, kernel_size=ks, stride=stride)

3、fcn函数——用于生成train.prototxt和val.prototxt

前部分是为了进行参数的设定

#用于生成train.prototxt和val.prototxt的函数
#输入参数split为'train'或'val'
def fcn(split):
    n = caffe.NetSpec() #使用pycaffe定义Net
    #参数设定
    pydata_params = dict(split=split, mean=(104.00699, 116.66877, 122.67892),
            seed=1337)
    if split == 'train':
        pydata_params['sbdd_dir'] = '../data/sbdd/dataset'
        pylayer = 'SBDDSegDataLayer'
    else:
        pydata_params['voc_dir'] = '../data/pascal/VOC2011'
        pylayer = 'VOCSegDataLayer'

接下来设置数据和标签的载入等等

其中的module是模型名称，一般对应自己所写的一个.py文件（用于实现自己想要的该层的功能，在这里对应voc_layers.py文件）

    n.data, n.label = L.Python(module='voc_layers', layer=pylayer,
            ntop=2, param_str=str(pydata_params))

网络结构组装

首先是前5层的卷积层

    # the base net
    n.conv1_1, n.relu1_1 = conv_relu(n.data, 64, pad=100)
    n.conv1_2, n.relu1_2 = conv_relu(n.relu1_1, 64)
    n.pool1 = max_pool(n.relu1_2)

    n.conv2_1, n.relu2_1 = conv_relu(n.pool1, 128)
    n.conv2_2, n.relu2_2 = conv_relu(n.relu2_1, 128)
    n.pool2 = max_pool(n.relu2_2)

    n.conv3_1, n.relu3_1 = conv_relu(n.pool2, 256)
    n.conv3_2, n.relu3_2 = conv_relu(n.relu3_1, 256)
    n.conv3_3, n.relu3_3 = conv_relu(n.relu3_2, 256)
    n.pool3 = max_pool(n.relu3_3)

    n.conv4_1, n.relu4_1 = conv_relu(n.pool3, 512)
    n.conv4_2, n.relu4_2 = conv_relu(n.relu4_1, 512)
    n.conv4_3, n.relu4_3 = conv_relu(n.relu4_2, 512)
    n.pool4 = max_pool(n.relu4_3)

    n.conv5_1, n.relu5_1 = conv_relu(n.pool4, 512)
    n.conv5_2, n.relu5_2 = conv_relu(n.relu5_1, 512)
    n.conv5_3, n.relu5_3 = conv_relu(n.relu5_2, 512)
    n.pool5 = max_pool(n.relu5_3)

可以看到第一个卷积层中conv1_1采用pad=100进行填充，这是为了防止输入图片过小（待会1/32的输入图片尺寸的特征图过小），同时这也是FCN可以输入任意大小图片进行训练和测试的原因，但这同时填充这么大会引入噪声

除了第一个卷积层中conv1_1采用pad=100进行填充外，conv1到conv5各卷积层的卷积核大小均为k=3，填充均为p=1（除了conv1_1）,步长均为s=1（详见刚刚conv_relu函数的解释）

由公式

可知：在这样的条件下，即输入尺寸等于输出尺寸

pool1-pool5各池化层的核大小均为k=2，填充均为p=0，步长均为s=2（详见刚刚max_pool函数的解释）

同样由上述公式可得出：，即输出尺寸等于输入尺寸的1/2。

所以通过第一个卷积层时，输出尺寸先增加了198，然后减半；接下来的2，3，4，5依次减半，即最后在增加198的基础上缩小了32倍的尺寸

在这里最后的输出是heat map（热图：高维特征图），不是我们通常说的普通的feature map

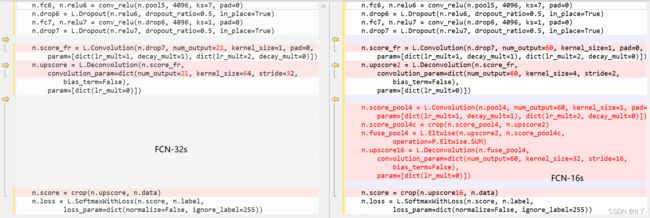
接下来是对应CNN的全连接层的替换

# fully conv
    n.fc6, n.relu6 = conv_relu(n.pool5, 4096, ks=7, pad=0)
    n.drop6 = L.Dropout(n.relu6, dropout_ratio=0.5, in_place=True)
    n.fc7, n.relu7 = conv_relu(n.drop6, 4096, ks=1, pad=0)
    n.drop7 = L.Dropout(n.relu7, dropout_ratio=0.5, in_place=True)
    n.score_fr = L.Convolution(n.drop7, num_output=21, kernel_size=1, pad=0,
        param=[dict(lr_mult=1, decay_mult=1), dict(lr_mult=2, decay_mult=0)])
    n.upscore = L.Deconvolution(n.score_fr,
        convolution_param=dict(num_output=21, kernel_size=64, stride=32,
            bias_term=False),
        param=[dict(lr_mult=0)])
    n.score = crop(n.upscore, n.data)
    n.loss = L.SoftmaxWithLoss(n.score, n.label,
            loss_param=dict(normalize=False, ignore_label=255))

    return n.to_proto()

第6层：先经过一次卷积后，然后采用dropout技术（正则化，减弱过拟合，失活系数为0.5）[补充：dropout技术——随机让网络的某些节点不工作（输出置零），也不更新权重，但会保存下来，下次训练还会用，只是本次训练不参与bp传播，其他过程不变。]

第7层：同样经过一次卷积，但是输入尺寸和输出尺寸一致，再次使用dropout技术，失活系数还是0.5

第8层：score_fr层+上采样层

score_fr层：VOC数据集共21类，所以输出为21（如果是其他数据集，需要修改这个输出），不改变尺寸大小

上采样层：通过反卷积来进行上采样

由公式得

score层：通过crop函数对上采样层进行裁剪，得到和data层一样的大小，即最终输出等于最初输入

总结：采用反卷积层对最后一个卷积层的feature map进行上采样, 让它恢复到输入图像相同的尺寸，从而对每个像素都产生了一个预测, 同时又保留了原始输入图像中的空间信息, 最后在上采样的特征图上进行逐像素分类。

---

四、FCN跳级结构原理解析

上述的网络结构其实已经可以实现图像分割了，但是直接将全卷积后的结果进行反卷积，得到的结果往往不太好看。

因此有了跳级结构——实现精细分割

从上面的分析可以得到我们有1/32尺寸的heatMap（第5层卷积层的输出），1/16尺寸的featureMap（第4层卷积层的输出）和1/8尺寸的featureMap（第3层卷积层的输出）。1/32尺寸的heatMap进行上采样操作之后，不能很好地还原图像当中的特征（因为这样的操作还原的图片仅仅是conv5中的卷积核中的特征）。

所以在这里向前迭代：

对于FCN-16s，首先对pool5 的输出进行2倍上采样获得2x upsampled feature，再把pool4的输出进行卷积和2x upsampled feature逐点相加，然后对相加的feature进行16倍上采样，并softmax prediction，获得16x upsampled feature prediction。

FCN-8s等原理与以上相同 

---

五、FCN跳级结构源码分析

这里以voc-fcn16s/net.py来阐述

其他的基本都和刚刚说的voc-fcn32s/net.py一样

以下是fully conv的代码

    # fully conv
    n.fc6, n.relu6 = conv_relu(n.pool5, 4096, ks=7, pad=0)
    n.drop6 = L.Dropout(n.relu6, dropout_ratio=0.5, in_place=True)
    n.fc7, n.relu7 = conv_relu(n.drop6, 4096, ks=1, pad=0)
    n.drop7 = L.Dropout(n.relu7, dropout_ratio=0.5, in_place=True)

    n.score_fr = L.Convolution(n.drop7, num_output=60, kernel_size=1, pad=0,
        param=[dict(lr_mult=1, decay_mult=1), dict(lr_mult=2, decay_mult=0)])
    n.upscore2 = L.Deconvolution(n.score_fr,
        convolution_param=dict(num_output=60, kernel_size=4, stride=2,
            bias_term=False),
        param=[dict(lr_mult=0)])

    n.score_pool4 = L.Convolution(n.pool4, num_output=60, kernel_size=1, pad=0,
        param=[dict(lr_mult=1, decay_mult=1), dict(lr_mult=2, decay_mult=0)])
    #对pool4的卷积
    n.score_pool4c = crop(n.score_pool4, n.upscore2)
    
    n.fuse_pool4 = L.Eltwise(n.upscore2, n.score_pool4c,
            operation=P.Eltwise.SUM)
    #逐点相加
    n.upscore16 = L.Deconvolution(n.fuse_pool4,
        convolution_param=dict(num_output=60, kernel_size=32, stride=16,
            bias_term=False),
        param=[dict(lr_mult=0)])

    n.score = crop(n.upscore16, n.data)
    n.loss = L.SoftmaxWithLoss(n.score, n.label,
            loss_param=dict(normalize=False, ignore_label=255))

    return n.to_proto()

其中不同的对比

---

欢迎大家在评论区批评指正，谢谢~