【论文笔记】Darts-可微神经架构搜索(一)
是什么
darts是什么?
全称 Differentiable ARchiTecture Search
它是一种新(2018)的NAS(神经架构搜索)方法。
NAS是什么?
全称: neural architecture search(神经架构搜索)
简单讲就是把设计神经网络的任务也交给机器。
企图把人工炼丹的过程一步步转化为机器炼丹。
具体说可以看看wiki上的定义:
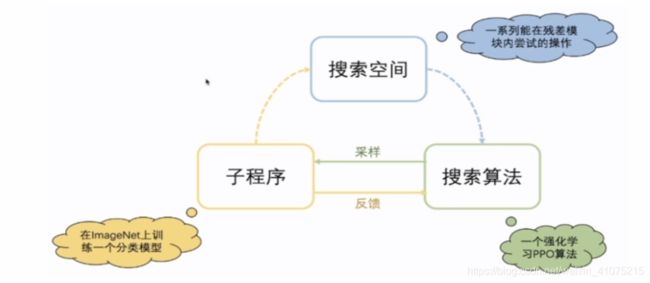
也就是一般的NAS都会包含三个部分:
-
搜索空间
-
搜索算法
-
预估算法(优化算法)
它们之间的关系可以大概用下面这个图表示
图源:VALSE_Webinar 20201223 Xuanyi Dong 侵删
NAS的一般流程也可以总结为:
-
定义一个搜索空间
-
通过一个搜索策略不断地去搭建模型,预估表现,根据预估再重新搭建模型
-
重复2直到收敛,找到搜出来那个最好的结构
为什么
上面的NAS流程问题在哪里?
问题在于每次找到一个新的模型,判断这个模型好坏是个麻烦事。
要是每个模型都train一遍吧,实在是太慢了(2000 gpu days),可要是不train吧,那怎么判断搜到的模型是好是坏?
这时,darts就出现了,既然train太慢了,那就少 train 一点吧!
图源 成都卫视 谭谈交通 侵删
但是少train也不是简简单单减少数据集这么简单,得有一个足够好的优化算法,保证我每次虽然 train 的少,还能为下次迭代找到正确的方向。
一起来看看darts是怎么做的吧!
怎么做
darts 的搜索空间
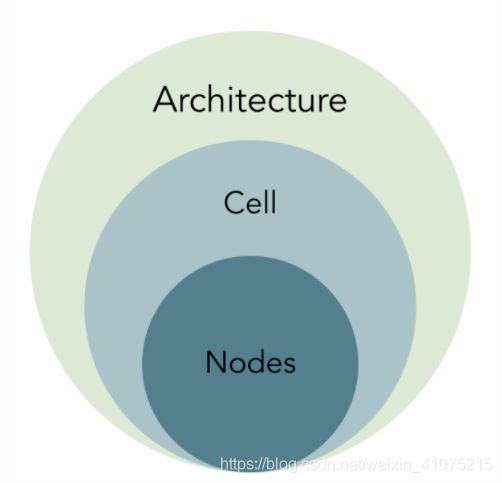
首先熟悉一下darts中的名词:
图源 知乎 @Kadima 侵删
首先,darts最后要得到的就是一个 Architecture,神经网络的总结结构,然后,darts内部预先定义好了8个cell,每个cell里面有4个node,每个node就是一个latent representation。(这些都是定好的,不能搜出来哦)
要搜索的就是,node之间如何连接,也就是节点之间的边:
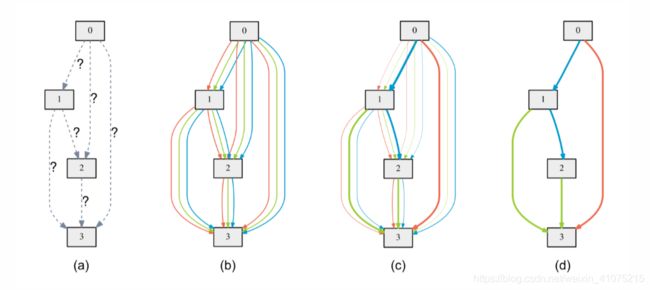
图源 darts论文 不删
是时候祭出原文中的这张图了。
可以看到,每个节点的输入,都是其所有前驱节点的输出,也就是说,如果是第二个node,那输入就是第一个node的输出。如果是第四个node,那输入就是前三个的输出。值得注意的是:
-
第一个node的输入是前两个cell的输出。
-
可选边类型包括zero,意味着这两个node并无边连接。
那这些可选的边,都包括哪些呢?
从代码可以看出来,可选的并不多:
PRIMITIVES = [ 'none', 'max_pool_3x3', 'avg_pool_3x3', 'skip_connect', 'sep_conv_3x3', 'sep_conv_5x5', 'dil_conv_3x3', 'dil_conv_5x5' ]
所以我们现在知道了,darts大概就是
选合适的边,给node连上。
idea挺直接的,那怎么做呢?
第一步:搜索空间连续化
这一步解决的就是,用softmax,让不同 边 共存,供算法后续的优化、选择。
具体来讲,就是原文中的这个公式:
大 O 就是刚才我们看到,代码里的八个操作,小o就是每个操作,α是每个操作的权重,最后 α杠 就是融合后的operation。
第二步:优化算法
现在问题来了,阿尔法(α)是个新的参数,每个不同的阿尔法(α)对应一个特殊的网络结构,也就意味着,每个阿尔法(α)都自己对应一组最优的网络参数 ,怎么优化这个问题呢?
论文对上述问题的描述,比我说的清晰:
首先,我们最终的目标函数,是优化公式3,也就是找到 loss 最小的那个阿尔法(α),但是得在w是最优时,才能比较不同阿尔法(α)的 loss,所以要满足公式2。
也就是要使得,这个 是当前阿尔法(α)的最优解。
当然,这是理想情况,现实找到这样的最优解太困难了,来看看 darts 是怎么做的:
-
第一步:优化阿尔法(α)
-
第二步:优化 。
第一步中有个小括号,熟悉的同学可能一眼就看出是个梯度下降的公式。
也就是说,不仅在第二步更新w,在第一步也更新一下。
这也就是论文中说的second order approximation,对应的 first order approximation 就没有这个小括号里得内容了。
这样做…对吗?
看完了对问题的形式化描述,也看完了darts提出的近似算法,很自然的想法是,这能work???
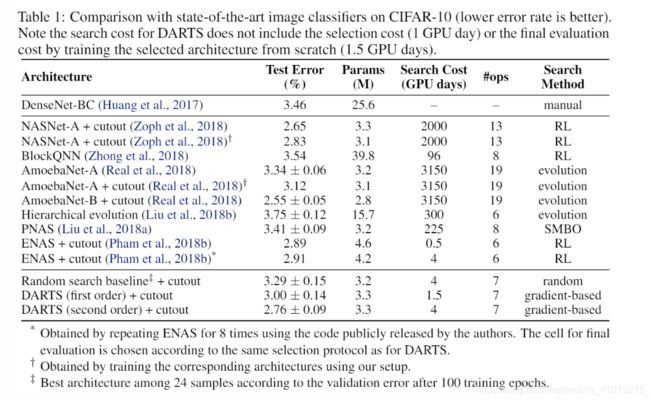
然而残酷的是,真的work
这结果还好滴很呢。
当然优秀的论文总不会满足于实验结果很好,文章里提出了两个很重要的问题,并作出了回答:
-
这样的优化方法,一定可以收敛吗?
-
这样的优化算法,找到的是全局最优解吗?
问题一,答案是不确定。找好学习率,实践上是可以的,理论上还不好说。
原文解释:
问题二:不是全局最优:
对于CNN,好像最后结果差不多,但是对于RNN,可以看到不同的初始化,结果能差四个点左右,足以证明得到的解并不是全局最优。
遗留的问题:
文章看完以后问题挺多,总结如下
第一:算法第一步为什么外层用val,里层用train?
第二:为什么这样做结果还不错呢?
如果我在第一步做两层优化呢?或者两步改成三步,第一步是优化w,第二步是优化阿尔法(α),第三步再优化w,这和原作一样吗?