CNN反向传播源码实现——CNN数学推导及源码实现系列(4)
前言
本系列文章链接:
CNN前置知识:模型的数学符号定义——卷积网络从零实现系列(1)_日拱一两卒的博客-CSDN博客![]() https://blog.csdn.net/yangwohenmai1/article/details/126951241?spm=1001.2014.3001.5501CNN前向/反向传播原理推导——卷积网络从零实现系列(2)_日拱一两卒的博客-CSDN博客
https://blog.csdn.net/yangwohenmai1/article/details/126951241?spm=1001.2014.3001.5501CNN前向/反向传播原理推导——卷积网络从零实现系列(2)_日拱一两卒的博客-CSDN博客![]() https://blog.csdn.net/yangwohenmai1/article/details/126622703?spm=1001.2014.3001.5501CNN前向传播源码实现——CNN数学推导及源码实现系列(3)_日拱一两卒的博客-CSDN博客
https://blog.csdn.net/yangwohenmai1/article/details/126622703?spm=1001.2014.3001.5501CNN前向传播源码实现——CNN数学推导及源码实现系列(3)_日拱一两卒的博客-CSDN博客![]() https://blog.csdn.net/yangwohenmai1/article/details/127230225?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22127230225%22%2C%22source%22%3A%22yangwohenmai1%22%7D 本文链接
https://blog.csdn.net/yangwohenmai1/article/details/127230225?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22127230225%22%2C%22source%22%3A%22yangwohenmai1%22%7D 本文链接
这个CNN系列是在学习图像识别过程中的一些学习笔记,包含理论分析和源码实现两部分。本质属于进阶内容,因此神经网络的基础内容不做过多讲解,想学习基础,可看之前的神经网络入门系列文章:人工智能专题研究_日拱一两卒的博客-CSDN博客
本系列重心放在解析CNN算法逻辑、前向和反向传播数学原理、推导过程、以及CNN模型的源码实现上。
本文详细讲解了CNN源码的实现过程,以及数据在CNN网络中流转的全过程,尽量做到每一行代码都讲解清楚,即是自己对知识做总结,也方便大家学习。本文是建立在前两篇文章的基础上,很多数学表达式不再重新推导,详细过程可查阅本系列第一篇和第二篇文章。
一、前情回顾
阅读本文前务必要先看上一篇文章,上篇文章讲解了卷积网络的前向传播流程,本文接着上篇文章继续讲解卷积网络的反向传播流程,用到的数据和变量均为上一篇文章的延续,所以要结合上篇文章才能看懂本文:
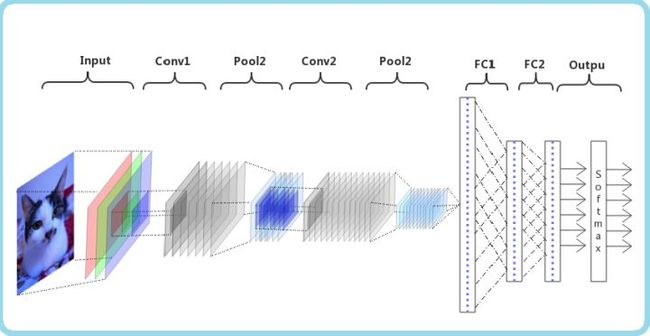
CNN前向传播源码实现——CNN数学推导及源码实现系列(3)_日拱一两卒的博客-CSDN博客CNN卷积网络的源码实现,以及数据在模型中流转的详细说明https://blog.csdn.net/yangwohenmai1/article/details/127230225?spm=1001.2014.3001.5501 开始讲解反向传播之前,再来回顾一下这篇文章的模型结构,如下图所示:
从上图可看到,本文所使用的模型结构如下,在后文中我们也会使用[卷积层1],[池化层1]这种表达形式带指代在模型的不同层上的反向传播的过程:
输入层=>卷积层1=>池化层1=>卷积层2=>池化层2=>FC1=>FC2=>softmax=>输出层
数据集输入:总量(60000, 1, 28, 28),每批次输入的数据张量是(32, 1, 28, 28)
卷积层1:使用5*5卷积核,卷积步长为1,输入通道为1 ,输出通道为32
池化层1:使用2*2视野域,步长为2
卷积层2:使用5*5卷积核,卷积步长为1,输入通道为32,输出通道为64
池化层2:使用2*2视野域,步长为2
全连接层1(FC1):输出为(32, 512)
全连接层2(FC2):输出为(32, 10)
softmax+输出层:输出为10
二、损失函数
关于损失函数,上一篇文章我们已经描述过代码如何实现,用的是[softmax+二元交叉熵]的组合,反向传播时softmax损失函数的求导过程比较复杂,之前的文章里已经详细讲解过,可以直接参看文章。损失函数反向传播的结果会传递到[全连接层2]中:
手动推导softmax神经网络反向传播求导过程——softmax前世今生系列(6)_日拱一两卒的博客-CSDN博客导读:softmax的前世今生系列是作者在学习NLP神经网络时,以softmax层为何能对文本进行分类、预测等问题为入手点,顺藤摸瓜进行的一系列研究学习。其中包含:1.softmax函数的正推原理,softmax的代数和几何意义,softmax为什么能用作分类预测,softmax链式求导的过程。2.从数学的角度上研究了神经网络为什么能通过反向传播来训练网络的原理。3.结合信息熵理论...https://forecast.blog.csdn.net/article/details/96741328
三、反向传播的实现与解析
反向传播分别包含两个卷积块[卷积层1,池化层1]、[卷积层2,池化层2],以及[全连接层1],[全连接层2]。两个卷积块之间和两个全连接层之间的计算流程都一样,所以文中把相似的模块合并起来写。在每个小节的标题上都会标注清楚,当前模块的输入所对应的输出源自哪里。
3.1.全连接层反向传播代码实现
第一节中提到:卷及网络模型包含两个全连接层,所以在反向传播中会两次调用全连接层反向传播算法。反向传播过程包含三个部分:1.激活函数求导,2.误差矩阵的传播,3.权重矩阵的更新。
3.1.1第一轮[全连接层2]反传播(上接[损失函数])
3.1.1.1.激活函数求导
此处[全连接层2]没有使用激活函数
3.1.1.2.误差矩阵的传播
下面代码中的deltaOri就是上篇文章中损失函数回传的误差矩阵deltaOri.shape(32, 10),w是当前全连接层在前向传播过程中所使用的权重矩阵w.shape(512, 10)。
从代码中可以看出,误差矩阵在全连接层的反向传播其实是进行了一次矩阵乘法运算。即误差矩阵deltaOri与全连接层的权重矩阵w的转置矩阵w.T进行相乘:
deltaOri.shape(32, 10) * w.T.shape(10, 512) => newdeltaOri.shape(32, 512)
3.1.1.3.权重矩阵参数的更新
getUpdWeights((w, b),(dw, db), lrt):最终将(w, b),(dw, db)传入getUpdWeights,函数使用Adam优化器进行梯度更新,也就是更新[全连接层1]中的权重矩阵w.shape(512, 10)和偏置项b.shape(10,)的参数。
3.1.2.第二轮全[连接层1]反传播(上接3.1.1对应的[全连接层2])
3.1.2.1.激活函数求导
本层[全连接层1]使用了ReLU激活函数,其求导非常简单,因为ReLU=max{0,x},所以x<=0时导数为0,x>0时导数为1。所以反向传播时小于0的部分直接取0,大于0的部分原样输出即可。
这里有一个要注意的点,判断反向传播的导数是否取0,是根据前向传播时产生的参数矩阵进行判断,而不是反向传播时的参数矩阵。原因是ReLU函数在前向传播时,小于0的参数不会继续向后传播(或者说以0值向后传播),所以反向传播时,原本以0值传播的位置也就不用将误差值向前反向传播,直接写0即可。
3.1.2.2.误差矩阵的传播
下面代码中的deltaOri就是上篇文章中损失函数回传的误差矩阵deltaOri.shape(32, 512),w是当前全连接层在前向传播过程中所使用的权重矩阵w.shape(3136, 512)。
从代码中可以看出,误差矩阵在全连接层的反向传播其实是进行了一次矩阵乘法运算。即误差矩阵deltaOri与全连接层的权重矩阵w的转置矩阵w.T进行相乘:
deltaOri.shape(32, 512) * w.T.shape(512, 3136) => (32, 3136)
3.1.2.3.权重矩阵参数的更新
getUpdWeights((w, b),(dw, db), lrt):最终将(w, b),(dw, db)传入getUpdWeights,使用Adam优化器进行梯度更新,也就是更新[全连接层2]中的权重矩阵w.shape(3136, )和偏置项b.shape(512,)的参数。
全连接层误差矩阵反向传播
# 误差矩阵反向传播
def bpDelta(self):
# 将通过激活函数求导后的误差矩阵deltaOri,和当前FCNN层的权重矩阵转置w.T相乘,来将误差向前传播
deltaPrevReshapped = Tools.matmul(self.deltaOri, self.w.T)
# 误差矩阵恢复之前Flatten()的拉伸变形,适配上层网络shape以便向上层网络继续反向传播
self.deltaPrev = deltaPrevReshapped if self.needReshape is False else deltaPrevReshapped.reshape(self.shapeOfOriIn)
return self.deltaPrev全连接层权重参数更新
# 计算反向传播权重梯度w,b
def bpWeights(self, input, lrt):
# dw = Tools.matmul(input.T, self.deltaOri)
# inputReshaped是正向传播时上层网络传到本层的输入矩阵,deltaOri是本层反向传播激活函数求导后的误差矩阵
dw = Tools.matmul(self.inputReshaped.T, self.deltaOri)
# 误差矩阵deltaOri.shape->(32,10),进行sum计算后将32个sample向量对应位置求和后db.shape->(1,10),再reshape成b.shape用于后续梯度优化
db = np.sum(self.deltaOri, axis=0, keepdims=True).reshape(self.b.shape)
# 当前层网络权重(w,b)元组
weight = (self.w,self.b)
# 反向传播的权重(dw,db)元组
dweight = (dw,db)
# 元组按引用对象传递,值在方法内部已被更新
# 将两个元组代入优化器,求出梯度方向,根据梯度更新参数,更新了self.lstmParams[i][Wx,Wh,b]的权重矩阵
self.optimizerObj.getUpdWeights(weight,dweight, lrt)3.2.池化层反向传播代码实现
这里一定要结合上一篇文章,首先回忆一下最大池化(max-pool)的原理,见文章,池化层的视野域为2*2,所以最大池化算法会从四个值中取最大的那一个,剩余3个值忽略。所以在反向传播过程中,对于前向传播时忽略的3个值的位置,我们在对应的位置直接补0,而在前向传播中取max值的位置,因为池化层本质上不涉及任何计算以及激活函数,所以我们将误差在对应的位置原样输出即可。平均池化则是将误差在4个位置均分,这里不再细讲。
3.2.1.第一轮[池化层2]反向传播(上接3.1.2对应的[全连接层1])
程序首先反推出池化层正向传播时输入张量的后两维大小input_size=14,用于确定最后反向传播的输出张量形式,此处方法不唯一。
dpool(32, 64, 7, 7):将上一层FC1反向传播来的误差矩阵dpool进行变形:dpool.shape(32, 3136) => dpool.shape(32, 64, 7, 7)
pool_idx(32, 64, 49, 4):是在前向传播时,我们记录的每个2*2池化块取max的位置,可参考上一篇文章的3.3.2节内容,pool_idx[3].count()=4这部分是one-hot类型编码,保存的是2*2池化块对应的四个取值位置,如[0,1,0,0]表示当前2*2的池化块在第2个位置取max。
pool_idx_reshape(32, 64, 14, 14):相当于将pool_idx里49个以4维one-hot编码的数据,转换成了14*14的矩阵结构,49*4 = 14*14,这样做是为了后续和结构为(32, 64, 14, 14)的误差矩阵dpool_i_tmp进行相乘。
dpool_reshape(32, 64, 49):dpool_reshape是由全连接层反向传播的误差矩阵dpool(32, 64, 7, 7)reshape而来,dpool_reshape[2].count()=49,这里保存的是[32个样例,64通道]中的49个反向传播的误差值。
dpool_i_tmp(32, 64, 14, 14):定义张量dpool_i_tmp,其后两维对应的是14*14的矩阵,包含49个2*2池化块,49*2*2=14*14。dpool_i_tmp的49个池化块用于接收误差矩阵dpool_reshape(32, 64, 49)中的49个误差值,把dpool_reshape中的49个误差值分别填充到dpool_i_tmp对应的每个2*2池化块中,每个2*2池化块包含的4个值都填充为其对应的同一个误差值。
dpool_i(32, 64, 14, 14):dpool_i_tmp(32, 64, 14, 14) * pool_idx_reshape(32, 64, 14, 14)通过矩阵乘法后,可将dpool_i_tmp中每个2*2的池化块中无需反向传播的3个位置都置零,最终只在前向传播时取max的位置保留了反向传播的误差值,得以将全连接层FC1传来的误差继续进行反向传播。
3.2.2.第二轮[池化层1]反向传播(上接3.3.1对应的[卷积层2])
池化层1反向传播过程和3.2.1完全相同,此处简化过程,只列出各个变量在模型中计算时的形态变化。如有疑问可以评论留言,会尽快回复。
dpool(32, 32, 14, 14)
pool_idx(32, 32, 196, 4)
pool_idx_reshape(32, 32, 28, 28)
dpool_reshape(32, 32, 196)
dpool_i_tmp(32, 32, 28, 28)
dpool_i(32, 32, 28, 28)
池化层反向传播代码实现
# bp4pool: 反向传播上采样梯度
# 入参:
# dpool: 池化层输出的误差项, N * 3136 =N*(64*7*7)= batches * (depth_i * pool_o_size * pool_o_size)
# reshape为batches * depth_i * pool_o_size * pool_o_size
# pool_idx : MAX pool时保留的max value index , batches * depth_i * y_o * x_per_filter
# pool_f_size: pool filter尺寸
# pool_stides:
# type : MAX ,MEAN, 缺省为MAX
# 返参:
# dpool_i: 传递到上一层的误差项 , batches * depth_i * pool_i_size * pool_i_size
# 当 strides =2 ,filter = 2 时, pool的pool_i_size 是pool_o_size 的2倍
def bp4pool(self, dpool, pool_idx, pool_f_size, pool_strides, type='MAX'):
logger.debug("bp4pool begin..")
batches = dpool.shape[0]
depth_i = pool_idx.shape[1]
y_per_o = pool_idx.shape[2]
# x_per_filter=2*2
x_per_filter = pool_f_size * pool_f_size
# -1.pool_o_size=7
# -2.pool_o_size=14
pool_o_size = int(np.sqrt(y_per_o))
# 反推输入的
# -1.input_size=14
# -2.input_size=28
input_size = (pool_o_size - 1) * pool_strides + pool_f_size
# reshape误差矩阵
# -1.dpool_reshape.shape(32, 64, 49)
# -2.dpool_reshape.shape(32, 32, 196)
dpool_reshape = dpool.reshape(batches, depth_i, y_per_o)
# -1.(32, 64, 14, 14)
# -2.(32, 32, 28, 28)
dpool_i_tmp = np.zeros((batches, depth_i, input_size, input_size), dtype=self.dataType)
pool_idx_reshape = np.zeros(dpool_i_tmp.shape, dtype=self.dataType)
for j in range(y_per_o):
b = int(j / pool_o_size) * pool_strides
c = (j % pool_o_size) * pool_strides
# pool_idx_reshape规格同池化层输入,每个block的max value位置值为1,其余位置值为0(池化层反向传播原理)
# 使用前向传播时保存的maxpooling索引矩阵pool_idx,将pool_idx池化取值元素位置信息反向传播到pool_idx_reshape对应位置
# -1.将pool_idx的j位置对应信息提取到pool_idx_reshape.shape(32, 64, 14, 14)。 pool_idx_reshape[::].shape=(32, 64, 2, 2), pool_idx[::].shape(32, 64, {j<=49隐藏}, 4).reshape(32, 64, 2, 2)
# -2.将pool_idx的j位置对应信息提取到pool_idx_reshape.shape(32, 32, 28, 28)。 pool_idx_reshape[::].shape=(32, 32, 2, 2), pool_idx[::].shape(32, 32, {j<=196隐藏}, 4).reshape(32, 32, 2, 2)
pool_idx_reshape[:, :, b:b + pool_f_size, c:c + pool_f_size] = pool_idx[:, :, j, 0:x_per_filter].reshape( batches, depth_i, pool_f_size, pool_f_size)
# dpool_i_tmp规格规格同池化层输入,每个block的值均以对应dpool元素填充
for row in range(pool_f_size): # 只需要循环 x_per-filter 次得到 填充扩展后的delta
for col in range(pool_f_size):
# -1.dpool_i_tmp[].shape=(32, 64, {<=14, <=14隐藏}) , dpool_reshape[].shape=(32, 64, {<=49隐藏})
# -2.dpool_i_tmp[].shape=(32, 64, {<=28, <=28隐藏}) , dpool_reshape[].shape=(32, 64, {<=196隐藏})
dpool_i_tmp[:, :, b + row, c + col] = dpool_reshape[:, :, j]
# 相乘后,max value位置delta向上传播,其余位置为delta为0
# -1.(32, 64, 14, 14) = (32, 64, 14, 14) * (32, 64, 14, 14)
# -2.(32, 32, 28, 28) = (32, 32, 28, 28) * (32, 32, 28, 28)
dpool_i = dpool_i_tmp * pool_idx_reshape
logger.debug("bp4pool end..")
return dpool_i3.3.卷积层反向传播代码实现
对于CNN层来说,误差矩阵反向传播时本质上仍然是与本层的卷积核进行一次卷积(互相关)计算,在进行卷积运算时要对卷积核翻转180度,卷积核翻转原理见下文的第四章第4节:
CNN前向/反向传播原理推导——卷积网络从零实现系列(2)_日拱一两卒的博客-CSDN博客![]() https://blog.csdn.net/yangwohenmai1/article/details/126622703?spm=1001.2014.3001.5501
https://blog.csdn.net/yangwohenmai1/article/details/126622703?spm=1001.2014.3001.5501
3.3.1.第一轮[卷积层2]反向传播(上接3.2.1对应的[池化层2])
x<=>d_o(32, 64, 14, 14):从上一层池化层反向传播来的误差矩阵
w(64, 32, 5, 5):卷积层对应的卷积核(权重矩阵),w.shape(输出通道,输入通道,卷积核长,卷积核高),卷积层没有权重矩阵只有卷积核
input(32, 32, 14, 14):当前卷积层在前向传播过程中的输入张量
w_rt(32, 64, 5, 5):对本层卷积核张量w进行180度反转后的结果,w.shape(64, 32, 5, 5) => w_rt.shape(32, 64, 5, 5)
3.3.1.1反向传播误差矩阵的算法
----begin conv_efficient(x=d_o, w_rt, 0, input_size, vec_idx_key, 1)
x<=>d_o:上一层反向传播来的误差矩阵
x_pad(32, 64, 18, 18):根据输入,卷积核,步长,推算出pading计算时填充的数据宽度p=2,然后对x进行padding补0填充,x.shape(32, 64, 14, 14) => x_pad.shape(32, 64, 18, 18)
--------begin vectorize4conv_batches(x_pad, filter_size, output_size, strides)
参数filter=5,output=14,对x_pad进行向量化转换,变成x_col,后续可以将卷积运算转换为矩阵乘积运算。
x_pad(32, 64, 18, 18) => x_col.shape(32, 64*5*5, 14*14) = x_col.shape(32, 1600, 196)
x_col(32, 1600, 196) = vectorize4conv_batches():x_col用于存储x_pad进行向量化转换之后的新张量
--------end vectorize4conv_batches
w_row(32, 1600):重构卷积核w.shape(32, 64, 5, 5)的维度,转化为与x_col.shape(32, 1600, 196)的维度对应的张量,方便后续w_row和x_col进行乘积计算,w.shape(32, 64, 5, 5) => w.shape(32, 64*5*5)
conv(32, 32, 196):构建张量conv.shape(32, 32, 14*14)用于存储翻转后的卷积核w_row和误差矩阵x_col[i]的卷积计算结果,conv[1].count()=32表示通道数,conv(32, 32, 196) = w_row.shape(32, 1600) * x_col[i].shape(1600, 196) + b = {32, [(32, 1600)*(1600, 196)+0]},此处x_col.shape(32, 1600, 196),对x_col的第一维进行循环计算,此处进行了通道转换,将64通道的误差矩阵转换成了32通道
conv_return(32, 32, 14, 14):展开张量conv.shape(32, 32, 196),作为后续反向传播的误差矩阵,conv.shape(32, 32, 196) => conv_return.shape(32, 32, 14, 14)
d_i(32, 32, 14, 14) = conv_efficient():存储当前误差矩阵与180度反转后的卷积核之间进行卷积(互相关)运算后的结果,作为继续向下层反向传播的误差矩阵
----end conv_efficient
3.3.1.2.计算偏置向b的梯度
db=np.sum(np.sum(np.sum(d_o, axis=-1), axis=-1), axis=0).reshape(-1, 1) :计算偏置b的梯度,将每个d_o上的误差矩阵相加,分别先后对误差数组第3、2、0维求和,然后转换为shape为n行1列的b:
d_o.shape(32, 64, 14, 14) => db.shape(64, 1)
3.3.1.3.计算卷积核w的梯度
----begin conv4dw(self, x=input, w=d_o, output_size, b=0, strides=1, x_v=False)
x<=>input(32, 32, 14, 14):前向传播时的输入input张量
w<=>d_o(32, 64, 14, 14):上一层反向传播到本层的误差矩阵
x_pad(32, 32, 18, 18):根据输入,卷积核,步长,推算出padding计算时填充的数据宽度p=2,x.shape(32, 32, 14, 14) => x_pad.shape(32, 32, 14+2+2, 14+2+2) = x_pad.shape(32, 32, 18, 18)
--------begin vectorize4convdw_batches(x_pad, filter_size, output_size, strides)
参数filter_size=14, output_size=5。本函数对x_pad进行向量化转换,变成x_col,后续可以将卷积运算转换为矩阵乘积运算。
x_pad(32, 32, 18, 18) => x_col.shape(32, 32, 14*14, 5*5) = x_col.shape(32, 32, 196, 25)
x_col(32, 32, 196, 25) = vectorize4convdw_batches():存储向量化后的结果
--------end vectorize4convdw_batches
w_row(32, 64, 196):重构误差矩阵w.shape(32, 64, 14, 14)维度,转化为与x_col(32, 32, 196, 25)的维度对应的张量,方便后续计算,w.shape(32, 64, 14, 14) => w_row.shape(32, 64, 14*14)
conv(32, 32, 64, 25):构建张量conv.shape(32, 32, 64, 25),用于存储后续在i(batch)和j(channel)维度下输入张量x_col和误差矩阵w_row乘积的结果,conv[i, j] = w_row[i] * x_col[i, j],conv(32, 32, 64, 25) = conv[i, j].shape({<=32, <=32隐藏}, 64, 25) = w_row[i].shape({<=32 隐藏}, 64, 196) * x_col[i, j].shape({<=32, <=32 隐藏}, 196, 25)
conv_sum(32, 64, 25):对误差梯度矩阵conv第1维进行累加计算,conv.shape(32, 32, 64, 25) => np.sum(conv, axis=0)
conv(64, 32, 5, 5):用transpose而不是直接reshape避免错位,conv_sum(32, 64, 25) => conv.shape(64, 32, 5, 5)这里的维度转换是为了反向传播中调转新生成的误差矩阵输入(depth_o)输出(channel)值
dw(64, 32, 5, 5) = conv4dw:计算出来的卷积核的梯度
----end conv4dw
此时我们求解出了反向传播误差张量d_i,卷积核梯度dw,偏置项梯度db,那么下面我们就就可更新卷积核和偏置项的参数了。
d_i(32, 32, 14, 14) = conv_efficient()
dw(64, 32, 5, 5) = conv4dw()
db(64, 1) = np.sum(np.sum(np.sum(d_o, axis=-1), axis=-1), axis=0).reshape(-1, 1)
3.3.1.4.梯度更新优化器算法
getUpdWeights((w, b),(dw, db), lrt):最终将上面计算得到的参数(w, b),(dw, db)传入梯度下降优化函数getUpdWeights(),也就是更新CNN层中的卷积核w.shape(64, 32, 5, 5)和偏置项b.shape(64, 1)的参数。本文中使用Adam优化器进行梯度更新,关于优化器的知识可参考下面这篇文章:机器学习11种优化器推导过程详解(SGD,BGD,MBGD,Momentum,NAG,Adagrad,Adadelta,RMSprop,Adam,Nadma,Adamx)_日拱一两卒的博客-CSDN博客_机器学习优化器![]() https://blog.csdn.net/yangwohenmai1/article/details/124882119?spm=1001.2014.3001.5501
https://blog.csdn.net/yangwohenmai1/article/details/124882119?spm=1001.2014.3001.5501
3.3.2.第二轮[卷积层1]反向传播(上接3.2.2对应的[池化层1])
卷积层1反向传播过程和3.3.1完全相同,此处简化过程,只列出各个变量在模型中计算时的形态变化。如有疑问可以评论留言,会尽快回复。
对于CNN层来说,误差矩阵反向传播时本质上仍然是与本层的卷积核进行一次卷积(互相关)计算,在进行卷积运算时要对卷积核翻转180度,详细原理见:
x<=>d_o(32, 32, 28, 28)
w(32, 1, 5, 5)
input(32, 1, 28, 28)
w_rt(1, 32, 5, 5)
误差矩阵的反向传播
----begin conv_efficient(x=d_o, w_rt, 0, input_size, vec_idx_key, 1)
x<=>d_o:上一层反向传播来的误差矩阵
x_pad(32, 64, 18, 18)
--------begin vectorize4conv_batches(x_pad, filter_size, output_size, strides)
filter=5,output=28,对x_pad进行向量化转换,后续可以将卷积运算转换为矩阵乘积运算
x_pad(32, 32, 32, 32) => x_col.shape(32, 32*5*5, 28*28) = x_col.shape(32, 800, 784)
x_col(32, 800, 784) = vectorize4conv_batches():x_col用于存储x_pad进行向量化转换之后的新张量
--------end vectorize4conv_batches
w_row(1, 800)
conv(32, 1, 784)
conv_return(32, 1, 28, 28)
d_i(32, 1, 28, 28) = conv_efficient()
----end conv_efficient
计算偏置向b的梯度
db=np.sum(np.sum(np.sum(d_o, axis=-1), axis=-1), axis=0).reshape(-1, 1) 计算偏置b的梯度,每个d_o上的误差矩阵相加,分别先后对误差数组第3、2、0维求和,然后转换为shape为n行1列的b
d_o.shape(32, 32, 28, 28) => db.shape(32, 1)
计算卷积核w的梯度
----begin conv4dw(self, x=input, w=d_o, output_size, b=0, strides=1, x_v=False)
x<=>input(32, 1, 28, 28)
w<=>d_o(32, 32, 28, 28)
x_pad(32, 1, 28, 28)
--------begin vectorize4convdw_batches(x_pad, filter_size, output_size, strides)
filter_size=28, output_size=5,对x_pad进行向量化转换,后续可以将卷积运算转换为矩阵乘积运算
x_pad(32, 1, 32, 32) => x_col.shape(32, 1, 28*28, 5*5) = x_col.shape(32, 1, 784, 25)
x_col(32, 1, 784, 25) = vectorize4convdw_batches():存储向量化后的结果
--------end vectorize4convdw_batches
w_row(32, 32, 784)
conv(32, 1, 32, 25)
conv_sum(1, 32, 25)
conv(32, 1, 5, 5)
dw(64, 32, 5, 5) = conv4dw
----end conv4dw
d_i(32, 1, 28, 28) = conv_efficient()
dw(32, 1, 5, 5) = conv4dw
db(32, 1) = np.sum(np.sum(np.sum(d_o, axis=-1), axis=-1), axis=0).reshape(-1, 1)
getUpdWeights((w, b),(dw, db), lrt):最终将(w, b),(dw, db)传入getUpdWeights,使用Adam优化器进行梯度更新,也就是更新CNN层中的卷积核w.shape(32, 1, 5, 5)和偏置项b.shape(32, 1)的参数
卷积层的的反向传播实现方法
# bp4conv: conv反向传播梯度计算
# 入参:
# d_o :卷积输出误差 batches * depth_o * output_size * output_size ,规格同 conv的输出
# w: depth_o * depth_i * filter_size * filter_size
# input: 原卷积层输入 batch * depth_i * input_size * input_size
# strides:
# 返参:
# d_i :卷积输入误差 batch * depth_i * input_size * input_size, 其中 depth_i为输入节点矩阵深度
# dw : w梯度,规格同w
# db : b 梯度 规格同b, depth_O * 1 数组
# vec_idx_key:
# 说明: 1.误差反向传递和db
# 将w翻转180度作为卷积核,
# 在depth_o上,对每一层误差矩阵14*14,以该层depth_i个翻转后的w 5*5,做cross-re得到 depth_i个误差矩阵14*14
# 所有depth_o做完,得到depth_o组,每组depth_i个误差矩阵
# batch * depth_o * depth_i * input_size * input_size
# d_i:每组同样位置的depth_o个误差矩阵相加,得到depth_i个误差矩阵d_i ,规格同a
# 优化, 多维数组w_rtLR, 在dept_o和dept_i上做转置,作为卷积和与d_o组协相关
# db: 每个d_o上的误差矩阵相加
# 2. dw
# 以d_o作为卷积核,对原卷积层输入input做cross-correlation得到 dw
# do的每一层depth_o,作为卷积核 14*14,
# 与原卷积的输入input的每一个depth_i输入层14*14和做cross-re 得到,depth_i个结果矩阵5*5
# 合计depth_o * depth_i * f_size * f_size
# 只要p/s =2 即可使结果矩阵和w同样规格,如 p=2,s=1
# 每个结果矩阵作为该depth_o上,该输入层w对应的dw。
def bp4conv(self, d_o, w, input, strides, vec_idx_key):
st = time.time()
logger.debug("bp4conv begin..")
# -1.input.shape(32, 32, 14, 14)
# -2.input.shape(32, 1, 28, 28)
input_size = input.shape[2]
# -1.w.shape(64, 32, 5, 5)
# -2.w.shape(32, 1, 5, 5)
f_size = w.shape[2]
# 卷积核w翻转180度(先上下翻转,再左右翻转),然后前两维互换实现多通道卷积核的“高维转置”(参考卷积求导原理)
# -1.(64, 32, 5, 5)
# -2.(32, 1, 5, 5)
w_rtUD = w[:, :, ::-1]
w_rtLR = w_rtUD[:, :, :, ::-1]
# -1.w_rt.shape(32, 64, 5, 5) w_rtLR(64, 32, 5, 5)
# -2.w_rt.shape(1, 32, 5, 5) w_rtLR(32, 1, 5, 5)
w_rt = w_rtLR.transpose(1, 0, 2, 3)
# 卷积层误差反向传播:误差矩阵向上反向传递,将卷积核180度反转后与误差矩阵做卷积运算即可
# -1.d_o.shape(32, 64, 14, 14) w_rt.shape(32, 64, 5, 5) d_i.shape(32, 32, 14, 14) input_size=14
# -2.d_o.shape(32, 32, 28, 28) w_rt.shape(1, 32, 5, 5) d_i.shape(32, 1, 28, 28) input_size=28
d_i = self.conv_efficient(d_o, w_rt, 0, input_size, vec_idx_key, 1)
logger.debug("d_i ready..")
# 下面计算梯度用于优化器optimizers
# 计算偏置b的梯度,每个d_o上的误差矩阵相加,分别先后对误差数组第3、2、0列求和,然后转换为shape为n行1列
# -1.d_o.shape(32, 64, 14, 14) -> db.shape(64, 1)
# -2.d_o.shape(32, 32, 28, 28) -> db.shape(32, 1)
db = np.sum(np.sum(np.sum(d_o, axis=-1), axis=-1), axis=0).reshape(-1, 1)
logger.debug("db ready.. %f s" % (time.time() - st))
# 计算卷积核w的梯度
# -1.input.shape(32, 32, 14, 14),d_o.shape(32, 64, 14, 14),f_size=5 dw.shape(64, 32, 5, 5),x_col(32, 32, 196, 25)
# -2.input.shape(32, 1, 28, 28),d_o.shape(32, 32, 28, 28),f_size=5 dw.shape(32, 1, 5, 5),x_col(32, 1, 784, 25)
dw, x_col = self.conv4dw(input, d_o, f_size, 0, 1, False)
logger.debug("bp4conv end.. %f s" % (time.time() - st))
return d_i, dw, db对误差矩阵向量化,然后进行卷积运算
# conv_efficient,使用向量化和BLAS优化的卷积计算版本
# 入参:
# x:前向传播时表示输入矩阵,反向传播时表示误差矩阵
# x规格: 根据x.ndim 判断入参的规格
# x.ndim=4:原始规格,未padding
# batch * depth_i * row * col, 其中 depth_i为输入节点矩阵深度,
# x.ndim=3:x_col规格,已padding
# batch * (depth_i * filter_size * filter_size) * (out_size*out_size)
# w规格: depth_o * depth_i * filter_size * filter_size , ,
# depth_o为过滤器个数或输出矩阵深度,depth_i和 x的 depth一致
# w_row: depth_o * (depth_i * filter_size * filter_size)
# b规格: 长度为 depth_o*1 的数组,b的长度即为过滤器个数或节点深度,和w的depth_o一致,可以增加校验。
# output_size:卷积输出尺寸
# strides: 缺省为1
# vec_idx_key: vec_idx键
# 返回: 卷积层加权输出(co-relation)
# conv : batch * depth_o * output_size * output_size
def conv_efficient(self, x, w, b, output_size, vec_idx_key, strides=1):
# 1.x.shape(32, 1, 28, 28)
# 2.x.shape(32, 32, 14, 14)
# -1.x.shape(32, 64, 14, 14)
# -2.x.shape(32, 32, 28, 28)
batches = x.shape[0]
depth_i = x.shape[1]
# 1.w.shape(32, 1, 5, 5)
# 2.w.shape(64, 32, 5, 5)
# -1.w.shape(32, 64, 5, 5)
# -2.w.shape(1, 32, 5, 5)
filter_size = w.shape[2]
# 输出通道个数
depth_o = w.shape[0]
if 4 == x.ndim: # 原始规格:
input_size = x.shape[2] #输入尺寸
# 根据filter_size计算padding尺寸
p = int(((output_size - 1) * strides + filter_size - input_size) / 2)
# logger.debug("padding begin..")
if p > 0:
# 1.对原始图像进行padding处理,p=2,(32, 1, 28, 28)->(32, 1, 32, 32)
# 2.对原始图像进行padding处理,p=2,(32, 32, 14, 14)->(32, 32, 18, 18)
# -1.对原始图像进行padding处理,p=2,(32, 64, 14, 14)->(32, 64, 18, 18)
# -2.对原始图像进行padding处理,p=2,(32, 32, 28, 28)->(32, 32, 32, 32)
x_pad = Tools.padding(x, p, self.dataType)
else:
x_pad = x
#st = time.time()
#logger.debug("vecting begin..")
# 使用向量化和BLAS优化的卷积计算,可以根据自己的硬件环境,在三种优化方式中选择较快的一种
# 1.filter=5,output=28,x_pad.shape(32, 1, 32, 32) => (32, 1*5*5, 28*28) = x_col.shape(32, 25, 784)
# 2.filter=5,output=14,x_pad.shape(32, 32, 18, 18) => (32, 32*5*5, 14*14) = x_col.shape(32, 800, 196)
# -1.filter=5,output=28,x_pad.shape(32, 64, 18, 18) => (32, 64*5*5, 1*14) = x_col.shape(32, 1600, 196)
# -2.filter=5,output=28,x_pad.shape(32, 32, 32, 32) => (32, 32*5*5, 28*28) = x_col.shape(32, 800, 784)
x_col = self.vectorize4conv_batches(x_pad, filter_size, output_size, strides)
#x_col = spd.vectorize4conv_batches(x_pad, filter_size, output_size, strides)
#x_col = vec_by_idx(x_pad, filter_size, filter_size,vec_idx_key,0, strides)
#logger.debug("vecting end.. %f s" % (time.time() - st))
else: # x_col规格
x_col = x
# 1.将权重w.shape(32, 1, 5, 5)转化为与卷积结果x_col对应的维度,方便计算,w_row.shape(32, 25)
# 2.将权重w.shape(64, 32, 5, 5)转化为与卷积结果x_col对应的维度,方便计算,w_row.shape(64, 800)
# -1.将权重w.shape(32, 64, 5, 5)转化为与卷积结果x_col对应的维度,方便计算,w_row.shape(32, 1600)
# -2.将权重w.shape(1, 32, 5, 5)转化为与卷积结果x_col对应的维度,方便计算,w_row.shape(1, 800)
w_row = w.reshape(depth_o, x_col.shape[1])
# 1.(32, 32, 28*28) 构建卷积输出shape,通道数为depth_o=32
# 2.(32, 64, 14*14) 构建卷积输出shape,通道数为depth_o=64
# -1.(32, 32, 14*14) 构建卷积输出shape,通道数为depth_o=32
# -2.(32, 1, 28*28) 构建卷积输出shape,通道数为depth_o=1
conv = np.zeros((batches, depth_o, (output_size * output_size)), dtype=self.dataType)
st1 = time.time()
logger.debug("matmul begin..")
#不广播,提高处理效率
for batch in range(batches):
# 1.conv.shape(32, 32, 784) = {32, [(32, 25)*(25, 784)+(32, 1)]}
# 2.conv.shape(32, 64, 196) = {32, [(64, 800)*(800, 196)+(64,1)]}
# -1.conv.shape(32, 32, 196) = {32, [(32, 1600)*(1600, 196)+0]}
# -2.conv.shape(32, 1, 784) = {32, [(1, 800)*(800, 784)+0]}
conv[batch] = Tools.matmul(w_row, x_col[batch]) + b
logger.debug("matmul end.. %f s" % (time.time() - st1))
# 1.conv.shape(32, 32, 784)->conv_return.shape(32, 32, 28, 28)
# 2.conv.shape(32, 64, 196)->conv_return.shape(32, 64, 14, 14)
# -1.conv.shape(32, 32, 196)->conv_return.shape(32, 32, 14, 14)
# -2.conv.shape(32, 1, 784)->conv_return.shape(32, 1, 28, 28)
conv_return = conv.reshape(batches, depth_o, output_size, output_size)
return conv_return误差矩阵向量化方法
# cross-correlation向量化优化
# x_col = (depth_i * filter_size * filter_size) * (conv_o_size * conv_o_size)
# w: depth_o * ( depth_i/channel * conv_i_size * conv_o_size) = 2*3*3*3
# reshape 为 w_row = depth_o * (depth_i/channel * (conv_i_size * conv_o_size)) = 2 * 27
# conv_t= matmul(w_row,x_col)
# 得到 conv_t = depth_o * (conv_o_size * conv_size) = 2 * (3*3) =2*9
# 再 conv = conv_t.reshape ( depth_o * conv_o_size * conv_size) = (2*3*3)
# ------------------------------------
# 入参
# x : padding后的实例 batches * channel * conv_i_size * conv_i_size
# fileter_size :
# conv_o_size:
# strides:
# 返回
# x_col: batches *(channel* filter_size * filter_size) * ( conv_o_size * conv_o_size)
def vectorize4conv_batches(self, x, filter_size, conv_o_size, strides):
batches = x.shape[0]
channels = x.shape[1]
x_per_filter = filter_size * filter_size
shape_t = channels * x_per_filter
x_col = np.zeros((batches, channels * x_per_filter, conv_o_size * conv_o_size), dtype=self.dataType)
for j in range(x_col.shape[2]):
b = int(j / conv_o_size) * strides
c = (j % conv_o_size) * strides
x_col[:, :, j] = x[:, :, b:b + filter_size, c:c + filter_size].reshape(batches, shape_t)
return x_col对卷积核求梯度
# conv4dw,反向传播计算卷积核的梯度dw,用于梯度下降优化器
# 以上一层反向传播输出的误差矩阵为卷积核w,本卷积层fp时上一层的输入input作为x,对二者做卷积运算x*w,即可得到卷积核w的梯度
# 由于x的2,3维和w的1,2,3维在训练中是有意义的,所以只对这些维进行乘积计算
# 输入输出尺寸不变的过滤器 当s==1时,p=(f-1)/2
# 入参:
# x规格: 根据x.ndim 判断入参的规格
# x.ndim=4:原始规格,未padding
# batch * depth_i * row * col, 其中 depth_i为输入节点矩阵深度,
# x.ndim=3:x_col规格,已padding
# 前向:batch * (depth_i * filter_size * filter_size) * (out_size*out_size)
# 反向:batch * depth_i * ( filter_size * filter_size) * (out_size*out_size)
# 注意,反向传播时,x_col保持四个维度而不是前向传播的三个
# w规格: batches * depth_o * filter_size * filter_size , ,
# depth_o为过滤器个数或输出矩阵深度,
# w_row: batches * depth_o * ( filter_size * filter_size)
# 此处的w是反向传播过来卷积层输出误差,没有depth_i这个维度
# b规格: 长度为 depth_o*1 的数组,b的长度即为过滤器个数或节点深度,和w的depth_o一致。
# conv4dw时,b为0
# output_size:conv4dw的输出矩阵尺寸,对应原始卷积层w的尺寸
# strides: 缺省为1
# x_v : False x未作矢量化,True x已作向量化(对第一层卷积适用,每个mini-batch多个Iteration时可提速)
# 返回: 卷积层加权输出(co-relation)
# conv : batch * depth_o * depth_i * output_size * output_size
def conv4dw(self, x, w, output_size, b=0, strides=1, x_v=False):
# -1 x.shape(32, 32, 14, 14)
# -2 x.shape(32, 1, 28, 28)
batches = x.shape[0]
depth_i = x.shape[1]
# -1 卷积核尺寸,对应卷积层误差矩阵尺寸,w.shape(32, 64, 14, 14)
# -2 卷积核尺寸,对应卷积层误差矩阵尺寸,w.shape(32, 32, 28, 28)
filter_size = w.shape[2]
x_per_filter = filter_size * filter_size
depth_o = w.shape[1]
if False == x_v: # 原始规格:
input_size = x.shape[2]
# p=2
p = int(((output_size - 1) * strides + filter_size - input_size) / 2) # padding尺寸
if p > 0: # 需要padding处理
# -1 x.shape(32, 32, 14, 14) -> x_pad.shape(32, 32, 14+2+2, 14+2+2)
# -2 x.shape(32, 1, 28, 28) -> x_pad.shape(32, 1, 28+2+2, 28+2+2)
x_pad = Tools.padding(x, p, self.dataType)
else:
x_pad = x
logger.debug("vec4dw begin..")
# 重构误差矩阵,后续与卷积核做乘法
# -1 对x_pad向量化x_col.shape(32, 32, 196, 25)
# -2 对x_pad向量化x_col.shape(32, 1, 784, 25)
x_col = self.vectorize4convdw_batches(x_pad, filter_size, output_size, strides)
logger.debug("vec4dw end..")
else: # x_col规格
x_col = x
# 重构卷积核,后续与误差矩阵做乘法
# -1 w.shape(32, 64, 14, 14) -> w_row.shape(32, 64, 196)
# -2 w.shape(32, 32, 28, 28) -> w_row.shape(32, 32, 784)
w_row = w.reshape(batches, depth_o, x_per_filter)
# 构建误差梯度conv矩阵,存储batch和channel维度下误差矩阵和卷积核乘积的结果
# -1 conv.shape(32, 32, 64, 25)
# -2 conv.shape(32, 1, 32, 25)
conv = np.zeros((batches, depth_i, depth_o, (output_size * output_size)), dtype=self.dataType)
logger.debug("conv4dw matmul begin..")
for batch in range(batches):
for col in range(depth_i):
# -1 conv[,].shape({<=32, <=32隐藏}, 64, 25) = w_row[].shape({<=32 隐藏}, 64, 196) * x_col[,].shape({<=32, <=32 隐藏}, 196, 25)
# -2 conv[,].shape({<=32, <=1隐藏}, 32, 25) = w_row[].shape({<=32 隐藏}, 32, 784) * x_col[,].shape({<=32, <=1 隐藏}, 784, 25)
conv[batch, col] = Tools.matmul(w_row[batch], x_col[batch, col])
# 以下为对误差梯度矩阵conv进行累加计算
# -1 conv.shape(32, 32, 64, 25) -> conv_sum(32, 64, 25)
# -2 conv.shape(32, 1, 32, 25) -> conv_sum(1, 32, 25)
conv_sum = np.sum(conv, axis=0)
# 这里的维度转换是为了反向传播中调转新生成的误差矩阵输入(depth_o)输出(channel)值
# -1 transpose而不是直接reshape避免错位,conv_sum(32, 64, 25) -> conv.shape(64, 32, 5, 5)
# -2 transpose而不是直接reshape避免错位,conv_sum(1, 32, 25) -> conv.shape(32, 1, 5, 5)
conv = conv_sum.transpose(1, 0, 2).reshape(depth_o, depth_i, output_size, output_size)
logger.debug("conv4dw matmul end..")
return conv, x_col求卷积核梯度中用到的向量化方法
# vectorize4convdw_batches:用于反向传播计算dw的向量化
# ------------------------------------
# 入参
# x : padding后的实例 batches * channel * conv_i_size * conv_i_size
# fileter_size :
# conv_o_size:
# strides:
# 返回
# x_col: batches *channel* (filter_size * filter_size) * ( conv_o_size * conv_o_size)
def vectorize4convdw_batches(self, x, filter_size, conv_o_size, strides):
batches = x.shape[0]
channels = x.shape[1]
x_per_filter = filter_size * filter_size
x_col = np.zeros((batches, channels, x_per_filter, conv_o_size * conv_o_size), dtype=self.dataType)
for j in range(x_col.shape[3]):
b = int(j / conv_o_size) * strides
c = (j % conv_o_size) * strides
x_col[:, :, :, j] = x[:, :, b:b + filter_size, c:c + filter_size].reshape(batches, channels, x_per_filter)
return x_col四、总结
CNN网络模型相较于RNN网络还是相对复杂的,本系列用了相当长的时间进行整理和总结到最后落地成文字,每一次重新梳理都有对细节理解方面都有新收获。把脑海中的理解用代码实现,再用文字对逐行代码逐个过程进行描述,这个过程也修正了作者之前对细节上的一些错误理解。
网上有大量CNN原理和实现的文章,但大多数都是复制粘贴,内容也基本没有参考价值,甚至脱离代码实现去讲理论,导致很多文章讲解内容都是错的。本系列的本意是希望用详细易懂的方式把CNN的原理和过程呈现出来,即是给大家做参考,也是给自己做备忘。然而这个过程实现起来并不容易,详细导致繁琐,实现的效果和预想也还有差距。
由于篇幅限制,很多神经网络中过于基础的东西和细节就省略了,本系列算是中阶难度,所以阅读过程中有疑问的地方可以直接留言提出,作者看到会尽快回复。源码从0实现没有调用任何第三方机器学习类库,所以源代码部分内容较多,完整贴上来篇幅太大,后续会上传到GitHUb,地址先占坑:{addr}。
参考资料:
卷积神经网络(convolutional neural network, CNN)_有梦想的雨的博客-CSDN博客_卷积神经网络