神经网络的学习
神经网络的学习
参考:
基础知识1
基础知识2
基础知识3
相关代码教程
一、 单层简单神经网络
四个人去看电影,通过前面三个人的选择来预测小强的选择。很简单可以看出小强的选择取决于如花的选择,如图:
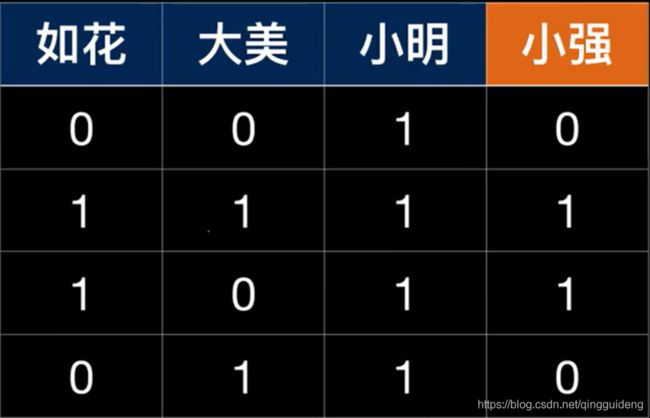 使用单层神经网络。
使用单层神经网络。

- 加载数据
X = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]]) # 对应着前面三位同学的选择
y = array([[0, 1, 1, 0]]).T # 对应着小强的选择,注意转置
- 设置初始的权重
random.seed(1) # 保证随机值都相同,每次的起点都是一样的
weights = random.random((3, 1)) * 2 - 1 # 生成3行1列的随机数,随机数范围[0,1], *2-1后的范围[-1,1]
- 前向传播forwardp
z = dot(X, weights) # 利用矩阵点乘一次性计算4个z出来,也就是预测小强的输出
output = 1 / (1 + exp(-z)) # 我们需要的是每个结果的概率,使用Sigmoid函数,最终结果会在(0,1)之间,计算最终的output
- 后向传播backp
error = y - output # 看看我们计算出来的和实际发生的有多大误差
# 计算斜率
slope = output * (1 - output) # sigmoid函数的斜率计算公式
# 计算增量
delta = error * slope # 增量的计算
- 更新参数
# 更新权重,针对每一个系数,要更新的值就是:每个样本的输入值x增量之和。
weights = weights + dot(X.T, delta) # X.T的一列和delta相乘,也就是如花的数据对delta的影响
整体代码如下:
# 1. 引入类库
from numpy import random, dot, exp, array
# 2. 加载数据
X = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]])
y = array([[0, 1, 1, 0]]).T
# 3. 设置随机权重
random.seed(1) # 保证随机值都相同
weights = random.random((3, 1)) * 2 - 1 # 生成3行1列的随机数,随机数范围[0,1], *2-1后的范围[-1,1]
# 4. 循环
for it in range(10000):
# 利用矩阵点乘一次性计算4个z出来
z = dot(X, weights)
# 使用Sigmoid函数,计算最终的output
output = 1 / (1 + exp(-z))
# 看看我们计算出来的和实际发生的有多大误差
error = y - output
# 计算斜率
slope = output * (1 - output) # sigmoid函数的斜率计算公式
# 计算增量
delta = error * slope # 增量的计算
# print(delta)
# 更新权重,针对每一个系数,要更新的值就是:每个样本的输入值x增量之和。
print(weights)
weights = weights + dot(X.T, delta) # X.T里 列表中如花数据对结果的影响
print(weights)
从结果可以看到,输出的结果和第一个,也就是“如花”的相关性很高。

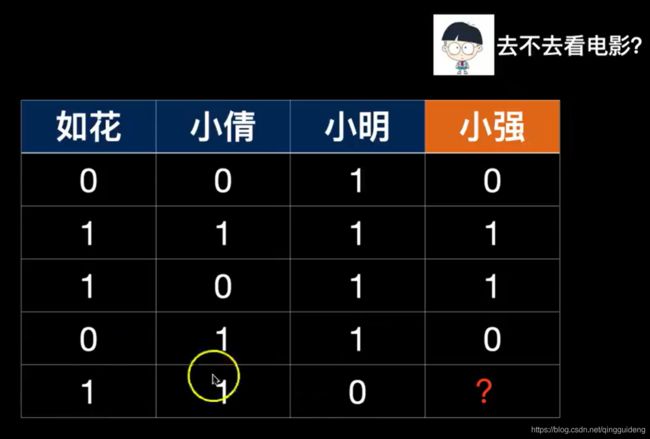
当我们想要进行预测的时候,我们先将代码重新整理一下。
当输入为(1,1,0)的时候,接近1。
当输入为(0,0,1)的时候,为提供的数据集数据,输出为0.009664,和第一条正确的数据吻合,说明效果不错。
# 深度神经网络的代码:
from numpy import random, dot, exp, array
# 正向推导:根据输入和权重,算出结果
def fp(input):
# 利用矩阵点乘一次性计算4个z出来
z = dot(input, weights)
# 使用Sigmoid函数,计算最终的output
return 1 / (1 + exp(-z))
# 反向转播:用计算结果和实际结果的误差,反向推算权重的调整量
def bp(y, output):
# 看看我们计算出来的和实际发生的有多大误差
error = y - output
# 计算斜率
slope = output * (1 - output) # sigmoid函数的斜率计算公式
# 计算增量
return error * slope
# 准备数据: X是输入参数, y是正确结果
X = array([[0, 0, 1], [0, 1, 1], [1, 0, 1], [1, 1, 1]])
y = array([[0, 0, 1, 1]]).T
random.seed(1)
weights = random.random((3, 1)) * 2 - 1 # 设置随机的权重,随机值*2再减1是为了让随机值在-1和1之间
for it in range(10000):
output = fp(X)
delta = bp(y, output)
weights = weights + dot(X.T, delta)
# print(weights)
print(fp([[0, 0, 1]]))
# [[0.009664]]
二、 深度神经网络
如果情况变成现在这样,我们依旧使用上面单层神经网络,是无法正确预测的。
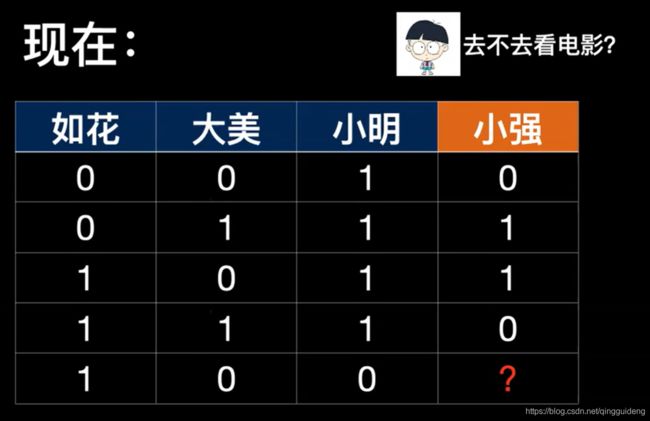
我们改成现在的数据集,再输出 当输入为(1,0,0)的时候的结果,发现结果为0.5。当输入(0,0,1)的时候,注意这个输入是在数据集中的,但这时的输出也是0.5。
# 深度神经网络的代码:
from numpy import random, dot, exp, array
# 正向推导:根据输入和权重,算出结果
def fp(input):
# 利用矩阵点乘一次性计算4个z出来
z = dot(input, weights)
# 使用Sigmoid函数,计算最终的output
return 1 / (1 + exp(-z))
# 反向转播:用计算结果和实际结果的误差,反向推算权重的调整量
def bp(y, output):
# 看看我们计算出来的和实际发生的有多大误差
error = y - output
# 计算斜率
slope = output * (1 - output) # sigmoid函数的斜率计算公式
# 计算增量
return error * slope
# 准备数据: X是输入参数, y是正确结果
X = array([[0, 0, 1], [0, 1, 1], [1, 0, 1], [1, 1, 1]])
y = array([[0, 1, 1, 0]]).T
random.seed(1)
weights = random.random((3, 1)) * 2 - 1 # 设置随机的权重,随机值*2再减1是为了让随机值在-1和1之间
for it in range(10000):
output = fp(X)
delta = bp(y, output)
weights = weights + dot(X.T, delta)
# print(weights)
print(fp([[1, 0, 0]]))
# 0.5
说明这个时候单层神经网络已经失效了,必须使用多层网络。

深度神经网络的代码如下:
此时,当输入已给定的数据时候,输出结果和正确的结果是一样的。
#深度神经网络的代码:
from numpy import random, dot, exp, array
#正向推导:根据输入和权重,算出结果
def fp(input):
l1 = 1/(1+exp(-dot(input, w0)))
l2 = 1/(1+exp(-dot(l1, w1)))
return l1, l2
#反向转播:用计算结果和实际结果的误差,反向推算权重的调整量
def bp(l1, l2, y):
#对于l2和l1之间
error = y - l2
slope = l2 * (1-l2)
l1_delta = error * slope
#对于l1和l0之间
l0_error = l1_delta.dot(w1.T) # w1*l1_delta
l0_slope = l1 * (1-l1)
l0_delta = l0_slope * l0_error
#计算增量
return l0_delta, l1_delta
#准备数据: X是输入参数, y是正确结果
X = array([[0,0,1],[0,1,1],[1,0,1],[1,1,1]])
y = array([[0,1,1,0]]).T
#设置随机的权重,随机值*2再减1是为了让随机值在-1和1之间
random.seed(1)
w0 = random.random((3,4)) * 2 - 1 # w0:输入到隐藏层之间的参数,定义3个输入,4个隐藏层神经元,则w0将是3*4=12个数据
w1 = random.random((4,1)) * 2 - 1 # w1:隐藏层到输出层之间的参数
#l0:输入层
#l1:隐藏层
#l2:输出层
for it in range(10000):
#正向推导
l0 = X
l1, l2 = fp(l0)
#反向传播
l0_delta, l1_delta = bp(l1, l2, y)
#更新权重
w1 = w1 + dot(l1.T, l1_delta)
w0 = w0 + dot(l0.T, l0_delta)
print(fp([[1,0,1]])[1])
# 0.99215207
