指派问题中匈牙利算法----Python实现

这里的匈牙利算法的理论部分可见胡运权所著的《运筹学教程》，本文对于理论部分只是简单介绍，主要是针对python实现进行讲解。

文章目录

一、指派问题

1.标准形式指派问题

2.非标准形式的指派问题

2.1.最大化指派问题

2.2.人数和事数不等的指派问题

2.3.一个人可做几件事的指派问题

2.4.某事一定不能由某人做的指派问题

二、匈牙利算法

1.算法流程

2.代码思路

 三、完整代码

总结

---

一、指派问题

指派问题是一个特殊的0-1规划问题。

1.标准形式指派问题

有n个人和n件事，已知第i人做第j事的费用为，要求确定人和事之间的一一对应的指派方案，使完成这n件事的总费用最少。

2.非标准形式的指派问题

非标准的指派问题可以转化为标准形式。一般有一下几种非标准形式。

2.1.最大化指派问题

寻找系数矩阵中最大元素m，将m分别减去矩阵中的每个元素，对其系数矩阵求解就可以得到与原问题相同最优解。

2.2.人数和事数不等的指派问题

添加一些虚拟的人或事儿，并添加的系数全为0，保证系数矩阵为方阵

2.3.一个人可做几件事的指派问题

若某个人可以做几件事，则可以将该人化作几个相同的人来接受指派，这几个人费用都一样

2.4.某事一定不能由某人做的指派问题

若某事一定不能由某人做，则可将相应的费用系数取足够大的数M。

二、匈牙利算法

1.算法流程

对于标准的指派问题，匈牙利解法的一般步骤如下：

1、对系数矩阵行规约和列规约，保证每一行每一列都有零元素

2、确定系数矩阵中的独立零元素。若独立零元素的个数要小于系数矩阵的维度，则进行转到步骤三；若个数等于系数矩阵的维度，则已经找到最优解。

3、继续变换系数矩阵，方法是在未被直线覆盖的元素中找到一个最小的元素，对未被直线所覆盖的行中各元素都减去这一最小元素。这样的操作会产生负元素，因此需要进一步消除负元素，对负元素所在的列中加上这一最小元素，得到新的系数矩阵，返回步骤2.

若要实现匈牙利算法，比较关键的部分就是确定独立零元素和找到覆盖所有零元素的最小直线数目的直线集合。

确定独立零元素需要确定零元素最少的一行，若这一行中零元素只有一个，则该零元素为独立零元素，否则，任取一个作为独立零元素。确定该独立零元素后，对同一列和同一行的零元素标号为，以此循环，找到所有的独立零元素。

而确定最小直线数目的直线集合的步骤较为简单（这里借鉴其他博客里面的部分）。如下

2.代码思路

代码思路：

上述所介绍的思路在实现时会有一些不同，如一些划线操作、对零元素标记的操作等不能像在纸上运算一样，会引入一些其他的变量进行操作。矩阵规约和步骤三里面的进一步变换矩阵，在此不进行介绍（因为实现起来很简单）。

独立零元素的确定：

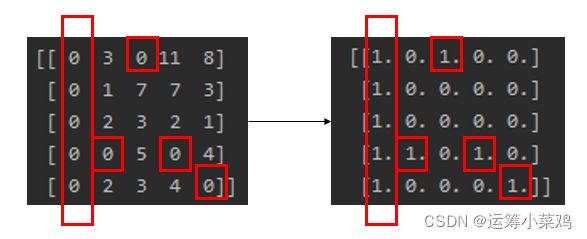
为确定独立零元素，需要将规约之后的系数矩阵中的0提取出来。标记每一个0出现的位置，在此引入一个新矩阵。如下图，其中1表示此位置有0。

接着对每一行1的个数进行统计，找到最少个数的行索引，从图中可知，第2行和第三行都只有一个0元素，在此，默认选择第一个，对同一行和同一列的其他0元素标记为-1，变换得到的矩阵为：

 进一步统计1的个数，同样选择最少的零元素的行，并且不能够选择已经选择的行索引，以此重复，最终第一次得到的系数矩阵如下，其中1表示独立零元素，-1表示，进入下一步划线，这一步很简单，就不做详细介绍了。

 

 三、完整代码

 完整代码如下，这里考虑的是标准形式的指派问题。

import numpy as np
import copy
#系数矩阵

"第一步进行行变换和列变换"
def preprocessing(C):
    #行规约
    row_change=np.min(C,axis=1)
    row_change=row_change.reshape(row_change.shape[0],1)
    C=C-row_change
    #列规约
    column_change=np.min(C,axis=0)
    C=C-column_change
    return C

'找到独立零元素'
def find_independent_zeros(C):
    #将系数矩阵中的0提取出来，若该位置为0，则标号1，否则为0
    zeroArray=np.zeros((C.shape[0],C.shape[1]))
    for i in range(C.shape[0]):
        num=0
        for j in range(C.shape[1]):
            if C[i,j]==0:
                num=1
                zeroArray[i,j]=num
    # print('标记零元素的矩阵',zeroArray)
    M=[]       #已经找到了独立0元素的行
    for j in range(5):
        '找到最少0值所在的行'
        countZero=np.count_nonzero(zeroArray==1,axis=1)     #统计每一行的零元素的个数
        #如果某一行已经确定了独立零元素，或者没有零元素，那么将计数列表提高一个极大数
        for i in range(len(countZero)):
            if countZero[i]==0 or i in M:
                countZero[i]=10000
        temp = np.argmin(countZero)  # 确定最少零元素个数的行索引
        M.append(temp)
        column = np.where(zeroArray[temp, :] == 1)[0]  # 一行中0元素的所有列索引

        #这里将同一行多余的0，提前设置为-1
        p=0
        for i in column:
            '第一个0不改变'
            if p==0:
                p+=1
            else:
                zeroArray[temp,i]=-1

        #这里将同一列多余0，设置为-1
        for k in range(C.shape[0]):
            if zeroArray[k, column[0]] == 1 and k not in M:
                zeroArray[k, column[0]] -= 2
        # print('确定某一行独立零元素后的矩阵',zeroArray)
    return zeroArray

'划线操作'
def draw_line(zeroArray,C):
    notZeroRow=[]      #没有独立零元素的行，并打✔
    for i in range(zeroArray.shape[0]):
        if 1 not in zeroArray[i,:]:
            notZeroRow.append(i)

    deletaZeroColumn=[]     #非独立零元素的列打✔
    for i in notZeroRow:
        for j in range(zeroArray.shape[0]):
            if zeroArray[i,j]==-1:
                deletaZeroColumn.append(j)

    #在已经✔的列中，对独立零元素的行打✔
    for i in deletaZeroColumn:
        for j in range(zeroArray.shape[0]):
            if zeroArray[j,i]==1:
                notZeroRow.append(j)

    '划线操作'
    lineListRow=[i for i in range(zeroArray.shape[0]) if i not in notZeroRow]
    lineListColumn=deletaZeroColumn
    findMin=copy.deepcopy(C)
    #将画线部分的值变为一个极大数
    for i in lineListRow:
        findMin[i,:]=100000
    for i in lineListColumn:
        findMin[:,i]=100000
    minIndex=np.where(findMin==np.min(findMin))
    for i in notZeroRow:
        C[i,:]-=findMin[minIndex[0][0],minIndex[1][0]]
    #消除负数元素
    for i in notZeroRow:
        for j in range(C.shape[0]):
            if C[i,j]<0:
                C[:,j]+=findMin[minIndex[0][0],minIndex[1][0]]
                break
    return C

if __name__ == '__main__':
    C = np.array([[4, 8, 7, 15, 12], [7, 9, 17, 14, 10], [6, 9, 12, 8, 7], [6, 7, 14, 6, 10], [6, 9, 12, 10, 6]])
    C_matrix=copy.deepcopy(C)
    '系数矩阵归一化处理'
    C_matrix=preprocessing(C_matrix)
    #确定独立零元素和划线操作
    while True:
        zeroArray=find_independent_zeros(C_matrix)
        if np.count_nonzero(zeroArray==1)==C.shape[0]:        #当独立零元素的个数等于系数方阵时，找到最优解
            break
        C_matrix=draw_line(zeroArray,C_matrix)

    '结果输出'
    result=np.where(zeroArray==1)
    cost=0
    for i in range(C.shape[0]):
        cost+=C[result[0][i],result[1][i]]
        print('事件',str(result[1][i]+1),'分配给工人',str(result[0][i]+1))
    print('总成本为：',cost)

运行结果：

---

 

总结

以上就是关于匈牙利解法求解指派问题的python实现。当然，在python中的Scipy库中有求解指派问题函数、或者直接使用Gurobi求解，这里只是用作学习算法用途。