python求解线性规划问题———单纯形法(一)
单纯形法(一)
——————————————————————————
——————————————————————————
!!2021-10-18更新
这篇文写了挺久了,也有蛮多人在看,也有不少错误被提出来。
看着自己以前写的代码也很烂(也很累),所以稍作修改。
——————————————————————————
——————————————————————————
1、为什么叫单纯形法
- 单纯形是N 维空间中的N+1 个顶点的凸包,是一个多胞体:直线上的一个线段,平面上的一个三角形,三维空间中的一个四面体等等,都是单纯形。
- 可以证明线性规划问题如果存在可行域,那么可行域必然是个凸集,其最优解必然在顶点取到——单纯形。
- 单纯形法的基本原理就是从可行域的一个顶点出发,不断转轴到下一个顶点从而最终找到最优解。
2、单纯形法怎么用
单纯形法的一般解题步骤可归纳如下:
- 1、把线性规划问题的约束方程组表达成典范型(标准型)方程组,找出基本可行解作为初始基本可行解。
- 2、若基本可行解不存在,即约束条件有矛盾,则问题无解。
- 3、若基本可行解存在,从初始基可行解作为起点,根据最优性条件和可行性条件,引入非基变量取代某一基变量,找出目标函数值更优的另一基本可行解。
- 4、按步骤3进行迭代,直到对应检验数满足最优性条件(这时目标函数值不能再改善),即得到问题的最优解。
- 5、若迭代过程中发现问题的目标函数值无界,则终止迭代。
3、我们先讨论最简单的情况:初始基本可行解已知
e.g.
m a x z = − 2 x 1 + x 2 s . t . { 3 x 1 + 2 x 2 + x 3 = 18 − x 1 + 4 x 2 + x 4 = 8 x i ≥ 0 , i = 1 , 2 , 3 , 4 max \ \ z=-2x_1+x_2 \\ s.t. \begin{cases} 3x_1+2x_2+x_3=18 \\ -x_1+4x_2+x_4=8 \\ x_i \geq0 \ ,i=1,2,3,4\end{cases} max z=−2x1+x2s.t.⎩⎪⎨⎪⎧3x1+2x2+x3=18−x1+4x2+x4=8xi≥0 ,i=1,2,3,4
可以很容易看出来 X = ( 0 , 0 , 18 , 8 ) T X=(0,0,18,8)^T X=(0,0,18,8)T是一个可行解;基变量选取为 x 3 , x 4 x_3,x_4 x3,x4,可以开始单纯形表的迭代。
4、py代码部分(简单使用了numpy库与fractions库)
使用到的包
a、获取所有的系数
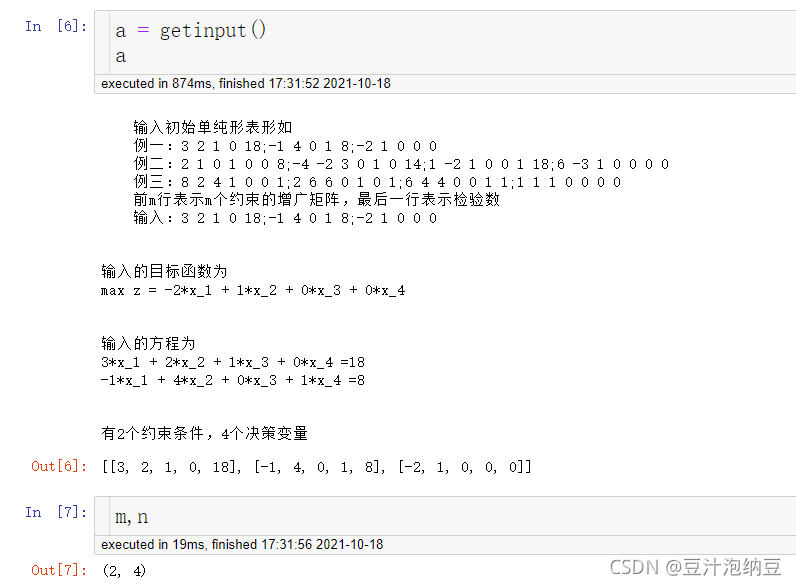
def getinput():
global m,n #这两个变量其他函数里也需要调用
string = input('''
输入初始单纯形表形如
例一:3 2 1 0 18;-1 4 0 1 8;-2 1 0 0 0
例二:2 1 0 1 0 0 8;-4 -2 3 0 1 0 14;1 -2 1 0 0 1 18;6 -3 1 0 0 0 0
例三:8 2 4 1 0 0 1;2 6 6 0 1 0 1;6 4 4 0 0 1 1;1 1 1 0 0 0 0
前m行表示m个约束的增广矩阵,最后一行表示检验数
输入:''')
a = [list(map(eval,row.split())) for row in string.split(';')]
matrix = np.array(a)
m,n = matrix.shape
n -= 1
m -= 1
print('\n\n输入的目标函数为')
x = [f'{matrix[-1,j]}*x_{j+1}' for j in range(n)]
print('max z = '+' + '.join(x))
print('\n\n输入的方程为')
for i in range(m):
x = [f'{matrix[i,j]}*x_{j+1}' for j in range(n)]
print(' + '.join(x),f'={matrix[i,-1]}')
print(f'\n\n有{m}个约束条件,{n}个决策变量')
return a
全局变量:m为约束数,n为决策变量数
b、判断是否需要转轴
matrix = np.array(a)
def judge(matrix):
if max(matrix[-1][:-1]) <= 0: # 最后一行除了b列的所有检验数
flag = False
else:
flag = True
return flag
输入一个numpy array数组,返回布尔值;
输入输出示例:

c、格式化输出单纯形表
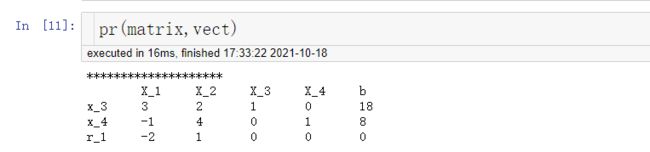
vect = [3, 4] #基变量足标
def pr(matrix,vect): #输出单纯形表
print('*'*20)
print(' ',end='\t')
for i in range(n):
print('X_{}'.format(i+1),end='\t')
print('b')
for i in range(m+1):
if i <= m-1:
print('x_{}'.format(vect[i]),end='\t')
elif i == m:
print('r_1',end='\t')
for j in matrix[i]:
print(f(str(j)).limit_denominator(),end='\t') #输出分数形式
print(end='\n')
d、转轴
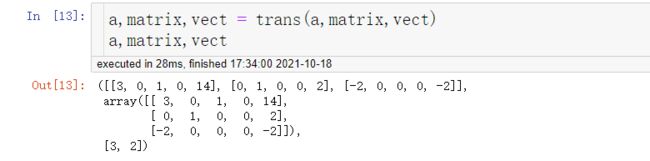
def trans(a,matrix,vect): #转轴
maxi = max(matrix[-1][:-1])
index = a[-1].index(maxi) #入基变量的足标
l = {}
for i in a[:-1]:
if i[index] >0:
l[i[-1]/i[index]] = a.index(i)
pivot = l[min(l)] #出基变量的足标
matrix[pivot] = matrix[pivot]/matrix[pivot][index]
for i in range(len(a)):
if i != pivot:
matrix[i] = matrix[i] - matrix[i][index]*matrix[pivot]
vect[pivot] = index+1 #基变量足标变化
a = [list(i) for i in matrix] #把原来的列表也同时变换掉,为了方便索引
return a,matrix,vect
示例:
e、格式化输出最优解
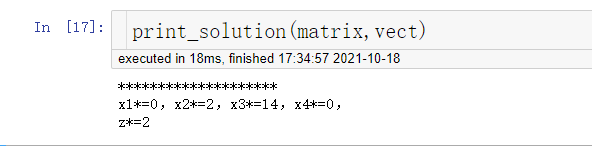
def print_solution(matrix,vect):
print('*'*20)
for i in range(1,n+1):
if i in vect:
print('x{}*={}'.format(i,f(str(matrix[vect.index(i)][-1])).limit_denominator()),end=',')
else:
print('x{}*={}'.format(i,0),end=',')
print('\nz*={}'.format(f(str(-matrix[-1][-1])).limit_denominator()))
f、主函数
def main():
a = getinput()
matrix = np.array(a, dtype=np.float64) #array可以方便地进行整行的操作,而列表可以方便索引
vect = [int(input('输入基变量足标')) for i in range(m)]
pr(matrix,vect)
while judge(matrix):
a,matrix = trans(a,matrix,vect)
pr(matrix,vect)
print_solution(matrix)
g、源代码及运行示例
from fractions import Fraction as f
import numpy as np
def getinput():
global m,n #这两个变量其他函数里也需要调用
string = input('''
输入初始单纯形表形如
例一:3 2 1 0 18;-1 4 0 1 8;-2 1 0 0 0
例二:2 1 0 1 0 0 8;-4 -2 3 0 1 0 14;1 -2 1 0 0 1 18;6 -3 1 0 0 0 0
例三:8 2 4 1 0 0 1;2 6 6 0 1 0 1;6 4 4 0 0 1 1;1 1 1 0 0 0 0
前m行表示m个约束的增广矩阵,最后一行表示检验数
输入:''')
a = [list(map(eval,row.split())) for row in string.split(';')]
matrix = np.array(a)
m,n = matrix.shape
n -= 1
m -= 1
print('\n\n输入的目标函数为')
x = [f'{matrix[-1,j]}*x_{j+1}' for j in range(n)]
print('max z = '+' + '.join(x))
print('\n\n输入的方程为')
for i in range(m):
x = [f'{matrix[i,j]}*x_{j+1}' for j in range(n)]
print(' + '.join(x),f'={matrix[i,-1]}')
print(f'\n\n有{m}个约束条件,{n}个决策变量')
return a
def judge(matrix):
if max(matrix[-1][:-1]) <= 0: # 最后一行除了b列的所有检验数
flag = False
else:
flag = True
return flag
def pr(matrix,vect): #输出单纯形表
print('*'*20)
print(' ',end='\t')
for i in range(n):
print('X_{}'.format(i+1),end='\t')
print('b')
for i in range(m+1):
if i <= m-1:
print('x_{}'.format(vect[i]),end='\t')
elif i == m:
print('r_1',end='\t')
for j in matrix[i]:
print(f(str(j)).limit_denominator(),end='\t') #输出分数形式
print(end='\n')
def trans(a,matrix,vect): #转轴
maxi = max(matrix[-1][:-1])
index = a[-1].index(maxi) #入基变量的足标
l = {}
for i in a[:-1]:
if i[index] >0:
l[i[-1]/i[index]] = a.index(i)
pivot = l[min(l)] #出基变量的足标
matrix[pivot] = matrix[pivot]/matrix[pivot][index]
for i in range(len(a)):
if i != pivot:
matrix[i] = matrix[i] - matrix[i][index]*matrix[pivot]
vect[pivot] = index+1 #基变量足标变化
a = [list(i) for i in matrix] #把原来的列表也同时变换掉,为了方便索引
return a,matrix,vect
def print_solution(matrix,vect):
print('*'*20)
for i in range(1,n+1):
if i in vect:
print('x{}*={}'.format(i,f(str(matrix[vect.index(i)][-1])).limit_denominator()),end=',')
else:
print('x{}*={}'.format(i,0),end=',')
print('\nz*={}'.format(f(str(-matrix[-1][-1])).limit_denominator()))
def main():
a = getinput()
matrix = np.array(a, dtype=np.float64) #array可以方便地进行整行的操作,而列表可以方便索引
vect = [int(input('输入基变量足标')) for i in range(m)]
pr(matrix,vect)
while judge(matrix):
a,matrix,vect = trans(a,matrix,vect)
pr(matrix,vect)
print_solution(matrix,vect)
if __name__ == '__main__':
main()
5、求解示例
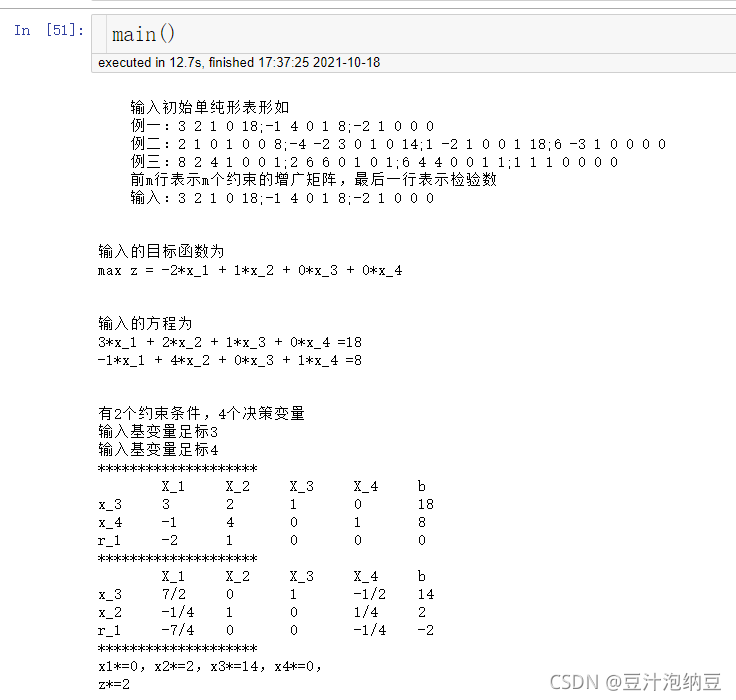
例一:
m a x z = − 2 x 1 + x 2 s . t . { 3 x 1 + 2 x 2 + x 3 = 18 − x 1 + 4 x 2 + x 4 = 8 x i ≥ 0 , i = 1 , 2 , 3 , 4 max \ \ z=-2x_1+x_2 \\ s.t. \begin{cases} 3x_1+2x_2+x_3=18 \\ -x_1+4x_2+x_4=8 \\ x_i \geq0 \ ,i=1,2,3,4\end{cases} max z=−2x1+x2s.t.⎩⎪⎨⎪⎧3x1+2x2+x3=18−x1+4x2+x4=8xi≥0 ,i=1,2,3,4
输入:
3 2 1 0 18;-1 4 0 1 8;-2 1 0 0 0
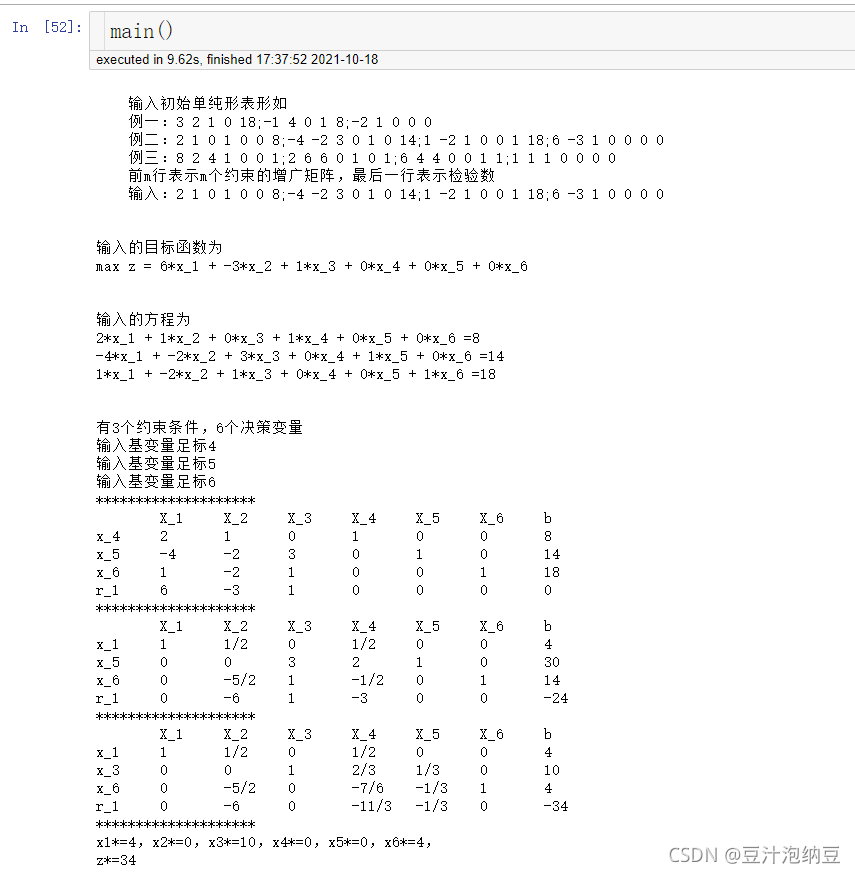
例二:
m a x z = 6 x 1 − 3 x 2 + x 3 s . t . { 2 x 1 + x 2 + x 4 = 8 − 4 x 1 − 2 x 2 + 3 x 3 + x 5 = 14 x 1 − 2 x 2 + x 3 + x 6 = 18 x i ≥ 0 , i = 1 , 2 , 3 , 4 , 5 , 6 max \ \ z=6x_1-3x_2+x_3 \\ s.t. \begin{cases} 2x_1+x_2+x_4=8 \\ -4x_1-2x_2+3x_3+x_5=14 \\ x_1-2x_2+x_3+x_6=18\\ x_i \geq0 \ ,i=1,2,3,4,5,6\end{cases} max z=6x1−3x2+x3s.t.⎩⎪⎪⎪⎨⎪⎪⎪⎧2x1+x2+x4=8−4x1−2x2+3x3+x5=14x1−2x2+x3+x6=18xi≥0 ,i=1,2,3,4,5,6
输入:
2 1 0 1 0 0 8;-4 -2 3 0 1 0 14;1 -2 1 0 0 1 18;6 -3 1 0 0 0 0
例三:
m a x x 1 + x 2 + x 3 s . t . { 8 x 1 + 2 x 2 + 4 x 3 + x 4 = 1 2 x 1 + 6 x 2 + 6 x 3 + x 5 = 1 6 x 1 + 4 x 2 + 4 x 3 + x 6 = 1 x i ≥ 0 , i = 1 , 2 , 3 , 4 , 5 , 6 max \ \ x_1+x_2+x_3\\ s.t. \begin{cases} 8x_1+2x_2+4x_3+x_4=1\\ 2x_1+6x_2+6x_3+x_5=1 \\ 6x_1+4x_2+4x_3+x_6=1 \\ x_i \geq0 \ ,i=1,2,3,4,5,6\end{cases} max x1+x2+x3s.t.⎩⎪⎪⎪⎨⎪⎪⎪⎧8x1+2x2+4x3+x4=12x1+6x2+6x3+x5=16x1+4x2+4x3+x6=1xi≥0 ,i=1,2,3,4,5,6
输入:
8 2 4 1 0 0 1;2 6 6 0 1 0 1;6 4 4 0 0 1 1;1 1 1 0 0 0 0