经济调度问题的建模及求解—考虑直流潮流(DC-OPF)与切负荷
潮流计算是电力系统分析的基础,其计算方式可粗略分为直流潮流和交流潮流。在前期推文 基于Distflow的最优潮流模型(OPF)–模型推导篇 发出后,有小伙伴在后台留言问我要潮流计算的代码,本期推文将给出直流潮流(DC-OPF)计算的相关代码。
直流潮流忽略了线路电阻和并联支路,同时不考虑无功与电压之间的关系,数学模型是一组线性方程[1],使得计算求解大为简化。因此,在文章 考虑风电经济调度的储能运行优化 的基础上,增加直流潮流和切负荷约束,实现风-火-储的经济调度。
Part 1、直流潮流与切负荷约束
-
直流潮流约束
在满足如下假设条件时[2]:
1)正常运行的电力系统各节点电压通常在额定电压附近,可以近似地认为 V i = V i = 1 V_{i}=V_{i}=1 Vi=Vi=1;
2)线路两端电压相角差很小,有 δ i j = 0 \delta_{i j}=0 δij=0,因此有 sin δ i j = 0 \sin \delta_{i j}=0 sinδij=0, cos δ i j = 1 \cos \delta_{i j}=1 cosδij=1;
3)超高压网络中,线路电阻比电抗小得多,电阻可以忽略, r i j = 1 r_{i j}=1 rij=1。
潮流方程就可以简化为:
P i j , t = δ i , t − δ j , t X i j \begin{aligned} P_{i j, t}=\frac{\delta_{i, t}-\delta_{j, t}}{X_{i j}} \end{aligned} Pij,t=Xijδi,t−δj,t
其中, P i j , t P_{i j, t} Pij,t 为 t t t 时刻节点 i i i 与节点 j j j 之间线路传输功率(MW), δ i , t \delta_{i, t} δi,t 为 t t t 时刻节点 i i i 的相角(rad), X i j X_{i j} Xij 为节点 i i i 与节点 j j j 之间线路的电抗(Ω)。
- 切负荷约束
0 ≤ L S i , t ≤ L i , t \begin{aligned} 0 \leq \mathrm{LS}_{i, t} \leq L_{i, t} \end{aligned} 0≤LSi,t≤Li,t
其中, L S i , t \mathrm{LS}_{i, t} LSi,t 为 t t t 时刻节点 i i i 的切负荷功率(MW), L i , t L_{i, t} Li,t 为 t t t 时刻节点 i i i 的负荷功率(MW)。储能、弃风及火电机组约束可参考历史推送: 考虑风电经济调度的储能运行优化 。因此,考虑直流潮流约束的风-火-储经济调度模型可以表示为:
O F = ∑ g , t a g ( P g , t ) 2 + b g P g , t + c g + ∑ i , t V O L L 2 × L S i , t + V W C × P i , t w c s . t . ∑ g ∈ Ω G i P g , t + L S i , t + P i , t w − L i , t − P i , t c + P i , t d = ∑ j ∈ Ω ℓ i P i j , t P i j , t = δ i , t − δ j , t X i j − P i j max ≤ P i j , t ≤ P i j max P g min ≤ P g , t ≤ P g max P g , t − P g , t − 1 ≤ R U g P g , t − 1 − P g , t ≤ R D g 0 ≤ L S i , t ≤ L i , t P i , t w c = w i , t Λ i w − P i , t w 0 ≤ P i , t w ≤ w t Λ i w S O C i , t = S O C i , t − 1 + ( P i , t c η c − P i , t d / η d ) Δ t P i , min c ≤ P i , t c ≤ P i , max c P i , min d ≤ P i , t d ≤ P i , max d S O C i , min ≤ S O C i , t ≤ S O C i , max \begin{aligned} \mathrm{OF}=&\sum_{g, t} a_{g}\left(P_{g, t}\right)^{2}+b_{g} P_{g, t}+c_{g}+\sum_{i, t} \mathrm{VOLL}^{2} \times \mathrm{LS}_{i, t}+\mathrm{VWC} \times P_{i, t}^{\mathrm{wc}} \\ s.t.&\sum_{g \in \Omega_{G}^{i}} P_{g, t}+\mathrm{LS}_{i, t}+P_{i, t}^{w}-L_{i, t}-P_{i, t}^{c}+P_{i, t}^{d}=\sum_{j \in \Omega_{\ell}^{i}} P_{i j, t} \\ &P_{i j, t}=\frac{\delta_{i, t}-\delta_{j, t}}{X_{i j}} \\ &-P_{i j}^{\max } \leq P_{i j, t} \leq P_{i j}^{\max } \\&P_{g}^{\min } \leq P_{g, t} \leq P_{g}^{\max } \\ &P_{g, t}-P_{g, t-1} \leq \mathrm{RU}_{g} \\&P_{g, t-1}-P_{g, t} \leq \mathrm{RD}_{g} \\ &0 \leq \mathrm{LS}_{i, t} \leq L_{i, t} \\ &P_{i, t}^{w c}=w_{i, t} \Lambda_{i}^{w}-P_{i, t}^{w} \\&0 \leq P_{i, t}^{w} \leq w_{t} \Lambda_{i}^{w} \\ &\mathrm{SOC}_{i, t}=\mathrm{SOC}_{i, t-1}+\left(P_{i, t}^{c} \eta_{c}-P_{i, t}^{d} / \eta_{d}\right) \Delta_{t} \\ &P_{i, \min }^{c} \leq P_{i, t}^{c} \leq P_{i, \max }^{c} \\ &P_{i, \min }^{d} \leq P_{i, t}^{d} \leq P_{i, \max }^{d} \\ &\mathrm{SOC}_{i, \min } \leq \mathrm{SOC}_{i, t} \leq \mathrm{SOC}_{i, \max }\end{aligned} OF=s.t.g,t∑ag(Pg,t)2+bgPg,t+cg+i,t∑VOLL2×LSi,t+VWC×Pi,twcg∈ΩGi∑Pg,t+LSi,t+Pi,tw−Li,t−Pi,tc+Pi,td=j∈Ωℓi∑Pij,tPij,t=Xijδi,t−δj,t−Pijmax≤Pij,t≤PijmaxPgmin≤Pg,t≤PgmaxPg,t−Pg,t−1≤RUgPg,t−1−Pg,t≤RDg0≤LSi,t≤Li,tPi,twc=wi,tΛiw−Pi,tw0≤Pi,tw≤wtΛiwSOCi,t=SOCi,t−1+(Pi,tcηc−Pi,td/ηd)ΔtPi,minc≤Pi,tc≤Pi,maxcPi,mind≤Pi,td≤Pi,maxdSOCi,min≤SOCi,t≤SOCi,max
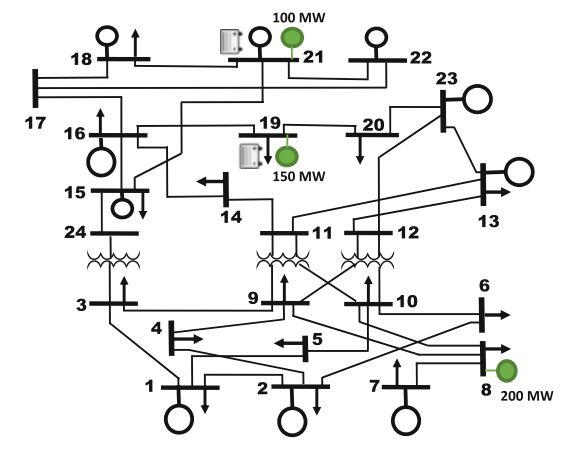
其中, a g a_{g} ag、 b g b_{g} bg、 c g c_{g} cg 表示发电机组的成本系数, P g , t P_{g, t} Pg,t 表示每个发电机组的输出功率,且 P g , t P_{g, t} Pg,t 满足发电上、下限约束和爬坡约束; P i , t c P_{i, t}^{c} Pi,tc 表示储能系统的充电功率; P i , t d P_{i, t}^{d} Pi,td 表示储能系统的放电功率; S O C i , t \mathrm{SOC}_{i, t} SOCi,t为储能系统的荷电状态; V O L L \mathrm{VOLL} VOLL 为切负荷惩罚价格; V W C \mathrm{VWC} VWC 为风电场弃风惩罚价格; Λ i w \Lambda_{i}^{w} Λiw为风电场实际发电功率(MW), P i , t w c P_{i, t}^{w c} Pi,twc 为弃风功率(MW), P i , t w P_{i, t}^{w} Pi,tw 为风力发电并网功率(MW)。本次推文的24节点系统图为:
Part 2、编程代码补充说明
- np.where(condition)函数的用法:用于寻找满足条件(condition)的索引值。
import numpy as np
a = np.array([1,3,5,7,9])
b = a[np.where(a>5)] #等价于 a[a>5]
c = np.where(a>5)
d = a[np.where(a==5)] #等价于 a[a=5]
print('a is',a)
print('b is',b)
print('c is',c)
print('d is',d)
示例:
RTS[“gen”][np.where(RTS[“gen”][:, 1] == 1)]表示利用np.where(RTS[“gen”][:, 1] == 1)在RTS[“gen”]的第2列([:, 1])中寻找1节点下(== 1)发电机的索引值;
- np.intersect1d函数的用法:查找两个数组中相同的值
import numpy as np
x = np.array([1, 1, 2, 3, 4])
y = np.array([2, 1, 4, 6])
Value_xy, Position_x, Position_y = np.intersect1d(x, y, return_indices=True)
print('The same value is',Value_xy)
print('The position of x is', Position_x+1)
print('The position of y is', Position_y+1)
示例:
x = np.where(RTS[“branch”][:, 0] == 1) # 第一列([:, 0])的1节点(== 1)
y = np.where(RTS[“branch”][:, 1] == 3) # 第二列([:, 1])的3节点(== 3)
RTS[“branch”][np.intersect1d(x, y)]利用np.intersect1d(x, y)判断RTS["branch "]中第1列的1节点索引和第2列3节点索引是否相同,若相同则返回索引表示1节点与3节点相连;若为空则表示1节点与3节点不相连。
- 代码中在每个节点设置了储能和风电场,增加了模型变量,在大规模问题中会增加求解时间,可根据具体案例情况进行修改减少变量个数,缩短求解时间;
- 在代码中,通过FS和RS枚举所有节点与支路的关联关系,避免了支路潮流重复计算,此处可以通过其他方法进一步改进。
Part 3、参考文献
[1] 赵晋泉,叶君玲,邓勇. 直流潮流与交流潮流的对比分析[J]. 电网技术,2012,36(10):147-152.
[2] 张伯明.陈寿孙.严正.高等电力网络分析[M].北京:清华大学出版社,2007.
[3] A. Soroudi, Power System Optimization Modeling in GAMS. 2017. DOI: 10.1007/978-3-319-62350-4.
Part 4、代码获取方式:
- 转发本推文至朋友圈集满88个赞即可免费获取代码;
- 转发本推文至朋友圈集满66个赞,同时赞赏5元,即可获取代码;
- 直接点击文末“喜欢作者”,赞赏10元,即可获取代码。
在满足上述任一条件后,请后台发送赞赏/点赞的截图获取代码链接,感谢大家的支持!
Part 5、创作人员名单
作者| 李同学1,李同学2
代码| 李同学1,李同学2
审核| 李同学2
往期内容回顾
16. 考虑风电经济调度的储能运行优化
15. 列与约束生成(Column and Constraint Generation, C&CG/CCG)算法
14. 考虑负荷灵敏度分析的火电机组经济调度
13. 拉格朗日乘子法与KKT条件
12. 经济调度问题的建模及求解——考虑爬坡约束
11. 火电机组经济调度建模及求解——基础篇
10. 基于Distflow的最优潮流模型(OPF)–模型推导篇
9. 火电机组经济调度建模及求解——基础篇
8. Python|Gurobi——零基础学优化建模-终章
7. Python|Gurobi——零基础学优化建模-压轴篇:多目标优化
6. Python|Gurobi——零基础学优化建模-分段模型线性化(PWL)
5. Python|Gurobi——零基础学优化建模-QCP
4. Python|Gurobi——零基础学优化建模-NLP
3. Python|Gurobi——零基础学优化建模-MIP
2. Python|Gurobi——零基础学优化建模-LP
1. Python|Gurobi——零基础学优化建模