3D激光里程计其一：ICP

Reference:

1. 深蓝学院-多传感器融合

1. ICP 整体流程

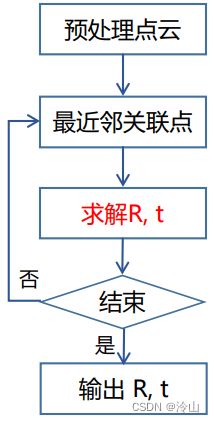
目的：有两个相似的刚体点云，它们之间没有做好配准，现在想将它们之间的旋转和平移找出来。

解决思路：如上图所示，从蓝色的点云里面选一些点，根据这些点，在红色的点云里面找离它最近的一些点，根据这些匹配点，可以将 R, t 计算出来。

存在问题：在找配准点的时候，找的点是最近的，但是找的这个点不见得是真正在刚体里面匹配的点。这个时候点找错了，那么根据这个点计算出来的 R, t，肯定是不精确的。就会出现中间图片的样子------两个刚体点云并没有完全重合。但是经过一次匹配后，俩点云至少更接近了，这时可以再做一次上面的流程。循环几次之后，可能就完全重合了。

2. ICP 的数学表示

• 点集：
  $$\begin{array}{rl}& X=\left\{x_1,x_2,\cdots ,x_{N_x}\right\}\\ & Y=\left\{y_1,y_2,\cdots ,y_{N_y}\right\}\end{array}$$

  其中 $X$ 和 $Y$ 是原始点云的子集，选取的是两个点集中能够互相关联的那些点，即 $N_x=N_y$。

• 目标：找到一组（R, t），使误差的二范数最小化
  $$\min E(R,t)=\min \frac{1}{N_y}\sum _{i=1}^{N_y}{\Vert x_i-R{y}_i-t\Vert }^2$$

3. 基于 SVD 的 ICP

SVD 的好处在于一步求解。完成了点的关联后，就可以通过一步运算将 R 和 t 求出来。
现在来看看公式上怎样解决这个问题：
$$\begin{array}{rl}E(R,t)& =\frac{1}{N_y}\sum _{i=1}^{N_y}{\Vert x_i-R{y}_i-t-u_x+R{u}_y+u_x-R{u}_y\Vert }^2\\ & =\frac{1}{N_y}\sum _{i=1}^{N_y}\left({\Vert x_i-u_x-R\left(y_i-u_y\right)+\left(u_x-R{u}_y-t\right)\Vert }^2\right)\\ & =\frac{1}{N_y}\sum _{i=1}^{N_y}\left({\Vert x_i-u_x-R\left(y_i-u_y\right)\Vert }^2+{\Vert u_x-R{u}_y-t\Vert }^2+2{\left(x_i-u_x-R\left(y_i-u_y\right)\right)}^T\left(u_x-R{u}_y-t\right)\right)\\ & =\frac{1}{N_y}\sum _{i=1}^{N_y}\left({\Vert x_i-u_x-R\left(y_i-u_y\right)\Vert }^2+{\Vert u_x-R{u}_y-t\Vert }^2\right)\\ & \end{array}$$

其中 $u_x$ 和 $u_y$ 分别是点集 $X$ 和 $Y$ 的质心，即：
$$u_x=\frac{1}{N_x}\sum _{i=1}^{N_x}{x}_i{u}_y=\frac{1}{N_y}\sum _{i=1}^{N_y}{y}_i$$

1. 在第一步加了几项进公式中：$-u_x+R{u}_y+u_x-R{u}_y$，用来化简方程；
2. 公式移项，就变成了$||a+b|{|}^2$这样了；
3. 根据$||a+b|{|}^2=||a|{|}^2+||b|{|}^2+2a^{T}b$，将公式拆开，可以发现 $2{\left(x_i-u_x-R\left(y_i-u_y\right)\right)}^T\left(u_x-R{u}_y-t\right)$ 的累加和为零。
   ${\sum }_{i=1}^{N_y}\left(x_i-u_x-R\left(y_i-u_y\right)\right)$，其中${\sum }_{i=1}^{N_y}(x_i-u_x)=0$，${\sum }_{i=1}^{N_y}R\left(y_i-u_y\right)=0$。

下面继续化简：
$$\begin{array}{rl}E(R,t)& =\frac{1}{N_y}\sum _{i=1}^{N_y}\left({\Vert x_i-u_x-R\left(y_i-u_y\right)\Vert }^2+{\Vert u_x-R{u}_y-t\Vert }^2\right)\\ & =E_1(R,t)+E_2(R,t)\end{array}$$

其中：$$\begin{array}{rl}& E_1(R,t)=\frac{1}{N_y}\sum _{i=1}^{N_y}{\Vert x_i-u_x-R\left(y_i-u_y\right)\Vert }^2\text{(只与旋转有关) }\\ & E_2(R,t)={\Vert u_x-R{u}_y-t\Vert }^2\text{(用于求平移部分) }\end{array}$$

可以发现的是，在$E_1$里面只有$R$没有$t$了。我们的目标是让$E_1+E_2$最小。在$E_1$里面，可以找到一个$R$，使结果最小。在$E_2$里面不管$R$是什么，都可以让$t=u_x-R{u}_y$，即这个值总是零。

因此，可以先根据$E_1(R,t)$求旋转，再根据$E_2(R,t)$求平移。

3.1 旋转部分求解

接下来就是看怎么把这个旋转求出来：
$$\begin{array}{rl}{E}_1(R,t)& =\frac{1}{N_y}\sum _{i=1}^{N_y}{\Vert x_i-u_x-R\left(y_i-u_y\right)\Vert }^2\\ & =\frac{1}{N_y}\sum _{i=1}^{N_y}{\Vert x_i^{\prime }-R{y}_i^{\prime }\Vert }^2\\ & =\frac{1}{N_y}\sum _{i=1}^{N_y}(x_i^{\prime T}{x}_i^{\prime }+y_i^{\prime }{R}^{T}R{y}_i^{\prime }-2x_i^{\prime T}R{y}_i^{\prime })\end{array}$$

用 $x_i^{\prime }$ 表示 $x_i-u_x$，$y_i^{\prime }$ 表示 $y_i-u_y$，公式展开。其中 ${x^{\prime }}_i^T{x^{\prime }}_i$ 与 $R$ 无关，而 $R^{T}R$ 是单位阵也没什么关系(旋转矩阵都是单位正交阵)。这时需要考虑的就只有 $-2x_i^{\prime T}R{y}_i^{\prime }$ 这一项了。令 ：
$$E_1^{\prime }(R,t)=\sum _{i=1}^{N_y}{x}_i^{\prime T}R{y}_i^{\prime }$$

则：
$$\begin{array}{rl}& \arg \underset{R}{\min }{E}_1(R,t)\\ =& \arg \underset{R}{\max }{E}_1^{\prime }(R,t)\\ =& \arg \underset{R}{\max }\sum _{i=1}^{N_y}{x}_i^{\prime T}R{y}_i^{\prime }\end{array}$$

即求最小的 $E_1$ 也就是求最大的 $x_i^{\prime T}R{y}_i^{\prime }$(因为该项带负号)。
E 1 ′ ( R , t ) = ∑ i = 1 N y x i ′ T R y i ′ ( 1 ) = ∑ i = 1 N y Trace ⁡ ( x i ′ T R y i ′ ) ( 2 ) = ∑ i = 1 N y Trace ⁡ ( R y i ′ x i ′ T ) = Trace ⁡ ( ∑ i = 1 N y R y i ′ x i ′ ) ( 3 ) = Trace ⁡ ( R H ) E_1^{\prime}(R, t)=\sum_{i=1}^{N_y} x_i^{\prime T} R y_i^{\prime}{}^{(1)}=\sum_{i=1}^{N_y} \operatorname{Trace}\left(x_i^{\prime T} R y_i^{\prime}\right)^{(2)}=\sum_{i=1}^{N_y} \operatorname{Trace}\left(R y_i^{\prime} x_i^{\prime T}\right)=\operatorname{Trace}\left(\sum_{i=1}^{N_y} R y_i^{\prime} x_i^{\prime}\right)^{(3)}=\operatorname{Trace}(R H) E1′​(R,t)=i=1∑Ny​​xi′T​Ryi′​(1)=i=1∑Ny​​Trace(xi′T​Ryi′​)(2)=i=1∑Ny​​Trace(Ryi′​xi′T​)=Trace ​i=1∑Ny​​Ryi′​xi′​ ​(3)=Trace(RH)

• 等式(1)：常数的迹等于它自身，因此上式是相等的
• 等式(2)：$\mathrm{tr}(AB)={\sum }_{i=1}^m{\sum }_{j=1}^n{a}_{ij}{b}_{ji}={\sum }_{i=1}^m{\sum }_{j=1}^n{b}_{ji}{a}_{ij}=\mathrm{tr}(BA)$
• 等式(3)：$H={\sum }_{i=1}^{N_y}{y}_i^{\prime }{x}_i^{\prime T}$

问题转化为，找到合适的 $R$，使 $\mathrm{Trace}(RH)$ 达到最大值。

• 定理：若有正定矩阵 $A{A}^T$ ，则对于任意正交矩阵 $B$ ，有 $\mathrm{Trace}(A{A}^T)\ge \mathrm{Trace}\left(BA{A}^T\right)$
  意义：若能找到 $R$，把 $\mathrm{Trace}(RH)$ 转换成 Trace $\left(A{A}^T\right)$ 的形式，则该 $R$ 就是我们要找的旋转矩阵证明(只要变成这种形式，再把$R$变成任意的旋转矩阵，都不可能比这个要大了。而我们的目标就是让这个值达到最大。)：
  $$\mathrm{tr}\left(BA{A}^T\right)=\mathrm{tr}\left(A^{T}BA\right)=\sum _i{a}_i^T\left(B{a}_i\right)$$

  其中 ${\mathrm{a}}_{\mathrm{i}}$ 为 $A$ 的列向量。根据柯西-施瓦茨不等式(有两向量$x、y$，$x^{T}y\le \sqrt{(x^{T}x)(y^{T}y)}$)，有
  $$a_i^T\left(B{a}_i\right)\le \sqrt{\left(a_i^T{a}_i\right)\left(a_i^T{B}^{T}B{a}_i\right)}=a_i^T{a}_i$$

  因此，
  $$\mathrm{tr}\left(BA{A}^T\right)=\sum _i{a}_i^T\left(B{a}_i\right)\le \sum _i{a}_i^T{a}_i=\mathrm{tr}\left(A{A}^T\right)$$

• 目的：找到 $R$，把 $\mathrm{Trace}(RH)$ 转换成 $\mathrm{Trace}\left(A{A}^T\right)$ 的形式
  方法：
  对 $H$ 进行SVD分解：$H=U\Sigma V^T$
  取 $R=V{U}^T$
  则有：$RH=V{U}^{T}U\Sigma V^T=V\Sigma V^T=V{\Sigma }^{\frac{1}{2}}{\Sigma }^{\frac{1}{2}}{V}^T=V{\Sigma }^{\frac{1}{2}}{\left(V{\Sigma }^{\frac{1}{2}}\right)}^T$
  其中 $U^{T}U$ 能消掉是奇异值分解中的性质。也就是说，找到了 $R=V{U}^T$，那就是要找的东西。

3.2 平移部分求解

旋转 $R$ 确定之后，可根据
$$E_2(R,t)={\Vert u_x-R{u}_y-t\Vert }^2$$

直接得到平移量为
$$t=u_x-R{u}_y$$

4. 基于优化的 ICP

优化的思想在于让点逐渐收敛，不想做 SVD 分解，就给一初值，让这个初值按照一定策略逐渐搜索，直到搜索到要的 R 和 t 满足一定条件，就认为得到了最终确定的结果。

非线性优化要求雅可比，而基于优化的ICP对应的雅可比推导在李代数模式下会更加简洁。ICP求解问题，可以重新表示为：
$$\underset{T}{\min }=\frac{1}{2}\sum _{i=1}^n{\Vert \left(x_i-T{y}_i\right)\Vert }_2^2$$

在李代数模式下，又可以重新表示为：
$$\underset{\xi }{\min }=\frac{1}{2}\sum _{i=1}^n{\Vert \left(x_i-\exp \left({\xi }^{\wedge }\right)y_i\right)\Vert }_2^2$$

其中 $\xi$ 为 $T$ 对应的李代数。
残差对应的雅可比为：
$$J=\frac{\partial e}{\partial \delta \xi }=-{\left(\exp \left({\xi }^{\wedge }\right)y_i\right)}^{\odot }$$
随后，便可根据优化的固定步骤求解位姿。

5. ICP 系列汇总