使用决策树相关算法实现波士顿房价预测

决策树浅析

决策树概述

决策树是一种经典的机器学习方法，其核心思想是相同(相似)的输入产生相同(相似)的输出。通过树状结果进行决策，其目的是通过对样本不同属性的判断决策，将具有相同属性的样本划分到下一个叶子节点，从而实现分类或者回归。

构建决策树

根据西瓜书的知识，构建决策树的算法如下:

由此可见决策树的构建是一个递归问题，核心在于：

• 如何选择最优的特征，使得对数据集的划分效果最好。
• 决定何时停止分裂节点。

选择决策特征

• 信息熵
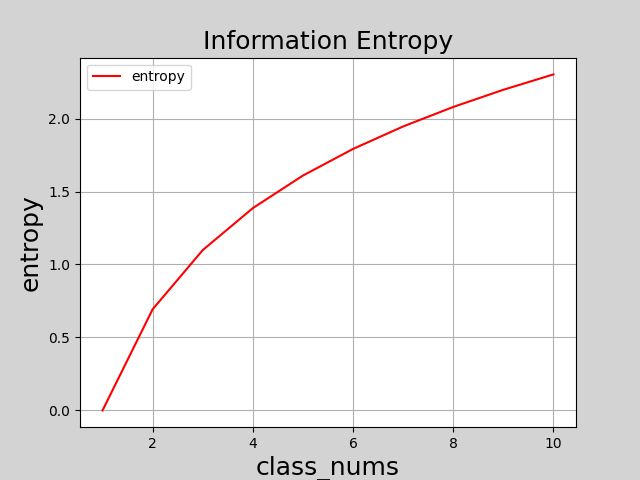
  信息熵(information entropy)是度量样本集合纯度的常用指标，改值越大，表示该集合纯度越低(混乱度越大)；该值越小，表示该集合纯度越高(混乱度越低)。信息熵定义如下：
  $$H=-\sum _{i=1}^{n}P(x_i)lo{g}_{2}P(x_i)$$
  其中，$P(x_i)$表示集合中第i类样本所占比例，当$P(x_i)=1$时(类别唯一，纯度最高)，此时$lo{g}_{2}P(x_i)=0$，整个系统的信息熵为0；当类别越多时，$P(x_i)$的值越接近于0，$lo{g}_{2}P(x_i)=0$越接近于无穷大，整个系统的信息熵就越大。可以通过以下代码展示类别数量逐渐变大时集合的信息熵变化。

import numpy as np
import math
import matplotlib.pyplot as plt

class_num = 10 # 最大类别数

def compute_entropy(n):
    p = 1.0/n # 假设类别等概率分布
    entropy_value = 0.0 # 信息熵
    for i in range(n):
        p_i = p * math.log(p)
        entropy_value += p_i
    
    return -entropy_value

entropies = [] # 记录信息熵用于可视化

for i in range(1, class_num+1):
    entropy = compute_entropy(i)
    entropies.append(entropy)

print('--------可视化--------')
plt.figure('Information Entropy', facecolor='lightgray')
plt.title('Information Entropy', fontsize=18)
plt.xlabel('class_nums', fontsize=18)
plt.ylabel('entropy', fontsize=18)
plt.plot(range(1,11), entropies, c='red', label='entropy')
plt.grid(':')
plt.legend()
plt.show()

• 信息增益
  决策树根据属性进行判断，将具有相同属性的样本划分到相同的节点下面，此时，样本较划分之前具有更高的纯度，信息熵值有所下降。此时，使用划分前的信息熵减去划分后的信息熵就可以得到决策树在划分前后获得的信息增益。信息增益表达式如下：
  $$Gain(D,a)=Ent(D)-\sum _{v=1}^V\frac{D^v}{D}Ent(D^v)$$
  其中，D表示样本集合，a表示属性，v表示属性a可能的取值种类(假设属性a具有3中不同的取值或者范围，则样本经过属性a划分之后最多是3分类)，$\frac{D^v}{D}$表示经过属性a划分之后每一个类别的权重。因此，Gain(D,a)表示样本集合上使用属性a划分前后获得的信息增益。
  
• 增益率
  增益率不直接使用信息增益，而是使用信息增益与信息熵的比值作为衡量特征优劣的标准，C4.5算法就是使用增益率作为标准选择最优划分属性。增益率表达式：
  $$Gai{n}_{r}atio(D,a)=\frac{Gain(D,a)}{IV(a)}$$
  其中：
  $$IV(a)=-\sum _{v=1}^V\frac{D^v}{D}lo{g}_2\frac{D^v}{D}$$
• 基尼系数
  基尼系数表达式：
  $$Gini(p)=\sum _{k=1}^k{p}_k(1-p_k)=1-\sum _{k=1}^k{p}_k^2$$
  基尼系数反映了从数据集中随机选择两个样本，类别不一致的概率。因此，基尼系数越小，数据集的纯度越高。CART决策树(Classification And Regression Tree)使用基尼系数进行划分属性选择。数据集下根据属性a划分的基尼系数：
  Gini_index(D,a) $={\sum }_{v=1}^V\frac{D_v}{D}Gini(D_v)$

停止分裂的时刻

• 当前节点所有样本属于同一类别；
• 当前属性集为空;
• 样本取值相同；
• 当前节点包含的样本集合为空；
• 当前节点样本节点数量少于指定的数量

决策树实现波士顿房价预测问题(sklearn)

import sklearn.datasets as sd
import sklearn.utils as su
import sklearn.tree as st
import sklearn.metrics as sm

boston_data = sd.load_boston() # 加载标准化数据集
print(boston_data.feature_names) # 属性名称
print(boston_data.data.shape) # 数据维度
print(boston_data.target.shape) # 标签维度

random_seed = 1 # 设置随机种子，固定随机值
x, y = su.shuffle(boston_data.data, boston_data.target,
                  random_state=random_seed)
train_size = int(len(x)*0.8) # 使用数据集中80%用作训练
# 切分数据集为训练集和测试集
train_x = x[:train_size]
test_x = x[train_size:]
train_y = y[:train_size]
test_y = y[train_size:]

# 构建模型
model = st.DecisionTreeRegressor(max_depth=4)
# 训练模型
model.fit(train_x, train_y)
# 预测
pred_test_y = model.predict(test_x)
# 使用R2系数进行回归模型预测评估
print('r2_score'%sm.r2_score(test_y, pred_test_y))

"""
['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
 'B' 'LSTAT']
(506, 13)
(506,)
r2_score: 0.886405
"""

特征重要性

作为决策树模型训练的副产品，根据每一个特征划分前后信息熵的减少量标志着该特征的重要程度，即为该特征重要性的指标。训练后得到的模型对象提供了属性**feature_importances_**存储每个特征的重要性。事实上，借此指标我们不必让每一个特征都参与划分，而选择相对更重要的特征参与划分。
加入下述代码可视化上述波士顿房价预测中各个属性的重要程度：

import matplotlib.pyplot as plt
import numpy as np

# 属性重要性程度可视化
fi = model.feature_importances_ 
plt.figure('Feature Importance', figsize=(8,6), facecolor='lightgray')
plt.title('Feature Importance', fontsize=18)
plt.ylabel('Feature Importance', fontsize=18)
plt.xlabel('attributes', fontsize=18)
plt.grid(linestyle=':', axis='x')
sorted_idx = fi.argsort()[::-1]
fi = fi[sorted_idx]
plt.xticks(np.arange(fi.size), boston_data.feature_names[sorted_idx])
plt.bar(np.arange(fi.size), fi, 0.6, color='dodgerblue', label='Feature Importances')
plt.legend()
plt.tight_layout()
plt.show()

集成学习

集成学习(ensemble learning)通过构建并合并多个模型来完成学习任务，从而获得比单一学习模型更优越的性能。形象来说，集成学习就是利用模型的’集体智慧’，提升预测的准确率。根据单个模型方式，集成学习可以分为两大类：

• 个体间存在依赖关系，必须串行生成的序列化方法，代表模型：Boosting算法；
• 个体间不存在强依赖关系，可同时生成的并行化方法，代表模型：Bagging和随机森林。

Boosting

Boosting时一族可以将弱学习器提升为强学习的算法，工作原理：

• 先训练一个初始模型；
• 根据模型的表现进行调整，使得模型预测错误的数据获得更多的关注即基于更大的权重，再重新训练下一个模型。
• 不断重复第二部，使得模型数量达到预先设定的数量，最终将这些训练过的模型加权结合。
  AdaBoosting时Boosting算法族中最著名的算法，其根据每一次训练集之中每一个样本的分类是否正确，以及上次的总体分类的准确率，来确定每一个样本的权值。将修改过权值的数据集送给下一层分类器进行训练，最后将每一次训练得到的分类器融合起来作为最后的决策分类器。
• sklearn之AdaBoosting接口

# model: 决策树模型（单个模型，基学习器）
model = st.DecisionTreeRegressor(max_depth=4)

# n_estimators：构建400棵不同权重的决策树，训练模型
model = se.AdaBoostRegressor(model, # 单模型
                             n_estimators=400, # 决策树数量
                             random_state=7)# 随机种子

随机森林

• 随机森林概述
  随机森林(Random Forest）是专门为决策树分类器设计的一种集成方法，是Bagging法的一种拓展，其是指每一次构建决策树模型时，不仅随机选择部分样本，而且随机选择部分特征构建多颗决策树。这样做不仅规避了强势样本对预测结果的影响，而且也削弱了强势特征的影响，使得模型具有更强的泛化能力。
  因此，随机森林计算开销小，在很多任务中都展现出很强大的性能，被誉为"代表集成学习技术水平的方法"。
• 使用sklearn实现随机森林

import sklearn.ensemble as se

model = se.RandomForestRegressor(
    max_depth, # 决策树最大深度
    n_estimators, # 决策树数量
    min_samples_split)# 节点分裂最小样本数目

利用随机森林处理波士顿房价预测(sklearn)

import sklearn.datasets as sd # sklearn标准化数据集加载模块
import sklearn.utils as su # sklearn工具模块
import sklearn.tree as st 
import sklearn.ensemble as se # sklearn集成学习模块
import sklearn.metrics as sm # sklearn模型评估模块

boston_data = sd.load_boston()
print(boston_data.feature_names)
print(boston_data.data.shape)
print(boston_data.target.shape)

random_seed = 1
x, y = su.shuffle(boston_data.data, boston_data.target, random_state=random_seed)
train_size = int(len(x)*0.8)
train_x = x[:train_size]
train_y = y[:train_size]
test_x = x[train_size:]
test_y = y[train_size:]

# 构建模型
model = se.RandomForestRegressor(max_depth=10, # 树的最大深度
                                 n_estimators=1000, # 树的数量
                                 min_samples_split=2 # 分裂最小样本数
                                )
# 训练模型
model.fit(train_x, train_y)
# 预测
pred_test_y = model.predict(test_x)
# 利用R2系数评估模型
r2_score = sm.r2_score(test_y, pred_test_y)
# 得到统计数据属性的重要性
fi = model.feature_importances_

print('r2_score', r2_score)

"""
['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
 'B' 'LSTAT']
(506, 13)
(506,)
r2_score 0.9051329154231126
"""

OK，以上就是关于决策树的一些较为浅显的认知，我想如果可以等到研究生阶段，这些模型如果有需要应该会更深入地探究。