各种注意力机制的PyTorch实现

一、符号说明

采用和PyTorch官方文档相似的记号：

符号	描述
$d_q$	查询向量的维度
$d_k$	键向量的维度
$d_v$	值向量的维度
$n$	查询的个数
$m$	键-值对的个数
$N$	批量大小
$L$	序列长度

导入本文所需要的包

import math
import torch
import torch.nn as nn
import torch.nn.functional as F

二、注意力评分函数

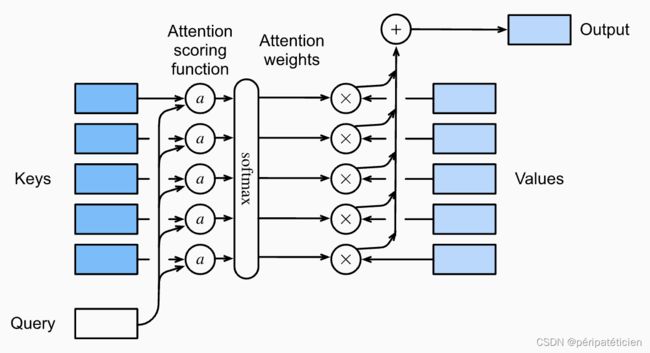
设有查询 $q$ 和 $m$ 个键-值对 $\{(k_i,v_i){\}}_{i=1}^m$，接下来我们会计算每一个 $a(q,k_i)$，其中 $a(\cdot ,\cdot )$ 是注意力评分函数，然后将其扔到softmax里得到 $m$ 个注意力权重 $\alpha (q,k_i)$，于是注意力机制的输出是一个向量：

$$\text{Attn}(q,\{(k_i,v_i){\}}_{i=1}^m)=\sum _{i=1}^m\alpha (q,k_i)v_i=\sum _{i=1}^m\text{softmax}(a(q,k_i))v_i$$

通常来讲，$m$ 个键-值对是固定的，但查询 $q$ 可能不止一个，有多少个查询注意力机制就会输出多少个向量，即：

$$\text{Attn}(\{q_i{\}}_{i=1}^n,\{(k_j,v_j){\}}_{j=1}^m)={\left\{\sum _{j=1}^m\text{softmax}(a(q_i,k_j))v_j\right\}}_{i=1}^n$$

下图形象地展示了注意力汇聚的过程

2.1 加性注意力

当 $d_q\ne d_k$ 时，通常使用加性注意力

$$a(Q,K)=\tanh (Q{W}_q+K{W}_k)W_v^{\mathrm{T}}$$

其中 $Q,K,W_v,W_q,W_k$ 的形状分别为 $(n,d_q),(m,d_k),(1,h),(d_q,h),(d_k,h)$。

因为 $Q{W}_q$ 和 $K{W}_k$ 的形状分别为 $(n,h)$ 和 $(m,h)$，不能直接相加，所以需要先将其形状分别扩展为 $(n,1,h)$ 和 $(1,m,h)$，然后再进行广播相加，得到形状为 $(n,m,h)$ 的张量。乘上 $W_v^{\mathrm{T}}$ 后，需要做一个 squeeze 操作，因此 $a(Q,K)$ 的形状为 $(n,m)$。

于是可得注意力汇聚函数为

$$\text{Attn}(Q,K,V)=\text{softmax}(\tanh (Q{W}_q+K{W}_k)W_v^{\mathrm{T}})V$$

其中 $\text{softmax}$ 操作在 $a(Q,K)$ 的最后一个维度上进行，$V$ 的形状为 $(m,d_v)$，最终得到的 $\text{Attn}(Q,K,V)$ 的形状为 $(n,d_v)$。

PyTorch实现如下：

class AdditiveAttention(nn.Module):
    def __init__(self, query_size, key_size, hidden_size):
        super().__init__()
        self.W_q = nn.Linear(query_size, hidden_size, bias=False)
        self.W_k = nn.Linear(key_size, hidden_size, bias=False)
        self.W_v = nn.Linear(hidden_size, 1, bias=False)

    def forward(self, query, key, value):
        """
        Args:
            query: (N, n, d_q)
            key: (N, m, d_k)
            value: (N, m, d_v)
        """
        query, key = self.W_q(query).unsqueeze(2), self.W_k(key).unsqueeze(1)
        attn_weights = F.softmax(self.W_v(torch.tanh(query + key)).squeeze(), dim=-1)  # (N, n, m)
        return attn_weights @ value  # (N, n, d_v)

这里的 @ 相当于 torch.bmm。

2.2 缩放点积注意力

当 $d_q=d_k\triangleq d$ 时，通常使用缩放点积注意力

$$a(Q,K)=\frac{Q{K}^{\mathrm{T}}}{\sqrt{d}}$$

其中 $Q,K$ 的形状分别为 $(n,d),(m,d)$，$a(Q,K)$ 的形状为 $(n,m)$。

于是可得注意力汇聚函数为

$$\text{Attn}(Q,K,V)=\text{softmax}\left(\frac{Q{K}^{\mathrm{T}}}{\sqrt{d}}\right)V$$

其中 $\text{softmax}$ 操作在 $a(Q,K)$ 的最后一个维度上进行，$V$ 的形状为 $(m,d_v)$，最终得到的 $\text{Attn}(Q,K,V)$ 的形状为 $(n,d_v)$。

PyTorch实现如下：

class ScaledDotProductAttention(nn.Module):
    def __init__(self):
        super().__init__()

    def forward(self, query, key, value):
        """
        Args:
            query: (N, n, d)
            key: (N, m, d)
            value: (N, m, d_v)
        """
        return F.softmax(query @ key.transpose(1, 2) / math.sqrt(query.size(2)), dim=-1) @ value

2.3 mask与dropout

先前我们实现的注意力评分函数为了简便起见没有引入掩码机制，一般而言我们会在注意力机制中加入mask和dropout，对于前者，具体会用到 masked_fill 方法，例如

a = torch.randn(4, 4)
print(a)
# tensor([[ 0.9105,  0.1080, -0.2465,  1.8417],
#         [ 0.2210,  0.3447, -2.0660,  0.7162],
#         [-0.0277, -0.0303, -0.4582, -0.6497],
#         [-0.1733,  0.9065,  0.5338,  1.0596]])
mask = torch.tensor([
    [False, False, False, True],
    [False, False,  True, True],
    [False,  True,  True, True],
    [True,   True,  True, True]
])  # mask不一定要与a的形状相同，只要能广播成a的形状即可
b = a.masked_fill(mask, 0)
print(b)
# tensor([[ 0.9105,  0.1080, -0.2465,  0.0000],
#         [ 0.2210,  0.3447,  0.0000,  0.0000],
#         [-0.0277,  0.0000,  0.0000,  0.0000],
#         [ 0.0000,  0.0000,  0.0000,  0.0000]])

对于后者，仅需调用 nn.Dropout 即可。

在引入mask和dropout后，两种注意力评分函数变为

class AdditiveAttention(nn.Module):
    def __init__(self, query_size, key_size, hidden_size, drouput=0):
        super().__init__()
        self.W_q = nn.Linear(query_size, hidden_size, bias=False)
        self.W_k = nn.Linear(key_size, hidden_size, bias=False)
        self.W_v = nn.Linear(hidden_size, 1, bias=False)
        self.dropout = nn.Dropout(drouput)

    def forward(self, query, key, value, attn_mask=None):
        """
        Args:
            query: (N, n, d_q)
            key: (N, m, d_k)
            value: (N, m, d_v)
            attn_mask: (N, n, m)
        """
        query, key = self.W_q(query).unsqueeze(2), self.W_k(key).unsqueeze(1)
        scores = self.W_v(torch.tanh(query + key)).squeeze()  # (N, n, m)
        if attn_mask is not None:
            scores = scores.masked_fill(attn_mask, float('-inf'))  # 经过softmax后负无穷的地方会变成0
        attn_weights = F.softmax(scores, dim=-1)  # (N, n, m)
        return self.dropout(attn_weights) @ value  # (N, n, d_v)

class ScaledDotProductAttention(nn.Module):
    def __init__(self, dropout=0):
        super().__init__()
        self.dropout = nn.Dropout(dropout)

    def forward(self, query, key, value, attn_mask=None):
        """
        Args:
            query: (N, n, d_k)
            key: (N, m, d_k)
            value: (N, m, d_v)
            attn_mask: (N, n, m)
        """
        assert query.size(2) == key.size(2)
        scores = query @ key.transpose(1, 2) / math.sqrt(query.size(2))
        if attn_mask is not None:
            scores = scores.masked_fill(attn_mask, float('-inf'))
        attn_weights = F.softmax(scores, dim=-1)
        return self.dropout(attn_weights) @ value

由于缩放点积注意力使用较为广泛，因此本文后半部分均采用该评分函数。
如果运行过程中出现了 nan，可尝试将 float('-inf') 替换为 -1e9 这种充分小的负数。

三、自注意力

设有序列 $x_1,x_2,\cdots ,x_L$，其中每个 $x_i$ 都是 embed_dim 维向量（已做了词嵌入）， 该序列的自注意力将输出一个长度相同的序列。

令

$$X={\left[\begin{array}{c}{x}_1^{\text{T}}\\ ⋮\\ x_L^{\text{T}}\end{array}\right]}_{L\times \text{embed\_dim}}$$

则自注意力函数为

$$\text{SelfAttn}(X)=\text{ScaledDotProductAttn}(X{W}_q,X{W}_k,X{W}_v)$$

其中 $W_q,W_k,W_v$ 的形状分别为 $(\text{embed\_dim},d_k),(\text{embed\_dim},d_k),(\text{embed\_dim},d_v)$。

PyTorch实现如下：

class SelfAttention(nn.Module):
    def __init__(self, embed_dim, key_size, value_size, dropout=0):
        super().__init__()
        self.attn = ScaledDotProductAttention(dropout)
        self.W_q = nn.Linear(embed_dim, key_size, bias=False)
        self.W_k = nn.Linear(embed_dim, key_size, bias=False)
        self.W_v = nn.Linear(embed_dim, value_size, bias=False)

    def forward(self, X, attn_mask=None):
        """
        Args:
            X: input sequence, shape: (N, L, embed_dim)
            attn_mask: (N, L, L)
        """
        query = self.W_q(X)  # (N, L, key_size)
        key = self.W_k(X)  # (N, L, key_size)
        value = self.W_v(X)  # (N, L, value_size)
        return self.attn(query, key, value, attn_mask)  # (N, L, value_size)

注意到 $q,k,v$ 的个数是相同的，均为 $L$，因此 attn_weights 的形状为 $(N,L,L)$，这说明自注意力的权重矩阵的形状是正方形。

在自注意力机制中，$Q,K,V$ 同源（都来源于同一个 $X$）。在后续的多头自注意力机制中，$Q,K,V$ 相等，即 $Q=K=V=X$。

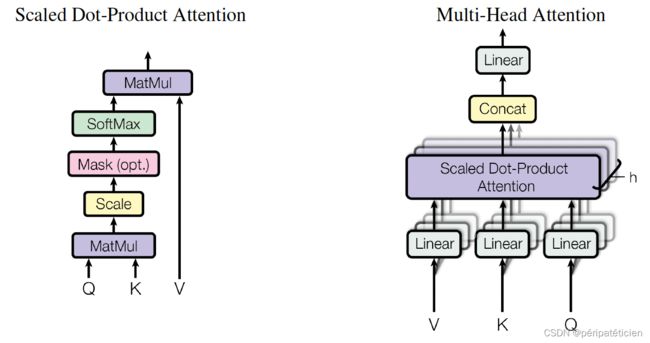
四、多头注意力

本节我们将从零开始（不依靠之前的代码）实现一个多头注意力机制。

图示：

具体而言，多头注意力可采用如下公式进行计算：

$$\begin{array}{rl}\text{MultiHeadAttn}(Q,K,V)& =\text{Concat}({\text{head}}_1,\cdots ,{\text{head}}_h)W^O\\ {\text{head}}_i& =\text{ScaledDotProductAttn}(Q{W}_i^Q,K{W}_i^K,V{W}_i^V)\end{array}$$

其中 $Q,K,V$ 的形状分别为 $(n,d_{\text{model}}),(m,d_{\text{model}}),(m,d_{\text{model}})$，$W_i^Q,W_i^K,W_i^V$ 的形状分别为 $(d_{\text{model}},d_k),(d_{\text{model}},d_k),(d_{\text{model}},d_v)$，$W^O$ 的形状为 $(h{d}_v,d_{\text{model}})$。

为实现并行计算，我们可以将 $h$ 个线性层合并在一起，即设 $W^Q,W^K,W^V$ 的形状分别为 $(d_{\text{model}},h{d}_k),(d_{\text{model}},h{d}_k),(d_{\text{model}},h{d}_v)$。根据原论文，为保证每一个sublayer输出的dimension都是 $d_{\text{model}}$，应有 $d_k=d_v=d_{\text{model}}/h$，从而 $W^Q,W^K,W^V$ 的形状均为 $(d_{\text{model}},d_{\text{model}})$，即线性变换不改变 $Q,K,V$ 的维度。

为保持与官方文档的记号一致，记 $d_{\text{model}}$ 为 embed_dim，$h$ 为 num_heads，则多头注意力机制的 __init__() 方法为

class MultiHeadAttention(nn.Module):
    def __init__(self, embed_dim, num_heads, dropout=0.0, bias=True):
        super().__init__()
        self.embed_dim = embed_dim  # 即d_model
        self.num_heads = num_heads  # 即注意力头数
        self.head_dim = embed_dim // num_heads  # 每个头的维度
        self.dropout = dropout
        assert self.head_dim * num_heads == embed_dim

        # 初始化W_Q,W_K,W_V,W_O
        self.q_proj = nn.Linear(embed_dim, embed_dim, bias=bias)
        self.k_proj = nn.Linear(embed_dim, embed_dim, bias=bias)
        self.v_proj = nn.Linear(embed_dim, embed_dim, bias=bias)
        self.out_proj = nn.Linear(embed_dim, embed_dim, bias=bias)

接下来定义一个私有方法用来计算缩放点积注意力

    def _scaled_dot_product_attention(self, q, k, v, attn_mask=None, dropout_p=0.0):
        """
        Args:
            q: (N, n, E), where E is embedding dimension.
            k: (N, m, E)
            v: (N, m, E)
            attn_mask: (n, m) or (N, n, m)
        
        Returns:
            attn_output: (N, n, E)
            attn_weights: (N, n, m)
        """
        q = q / math.sqrt(q.size(2))
        if attn_mask is not None:
            scores = q @ k.transpose(-2, -1) + attn_mask
        else:
            scores = q @ k.transpose(-2, -1)

        attn_weights = F.softmax(scores, dim=-1)
        if dropout_p > 0.0:
            attn_weights = F.dropout(attn_weights, p=dropout_p)
        attn_output = attn_weights @ v
        return attn_output, attn_weights

为了便于维护代码，我们在 forward 中调用私有方法进行前向传播的计算

    def forward(self, query, key, value, attn_mask=None, key_padding_mask=None):
        """
        Args:
            query: (n, N, embed_dim)
            key: (m, N, embed_dim)
            value: (m, N, embed_dim)
            attn_mask (bool Tensor or float Tensor): (n, m) or (N * num_heads, n, m)
            key_padding_mask (bool Tensor): (N, m)

        Returns:
            attn_output: (n, N, embed_dim)
            attn_output_weights: (N, num_heads, n, m)
        """
        return self._multi_head_forward_attention(query,
                                                  key,
                                                  value,
                                                  dropout_p=self.dropout,
                                                  attn_mask=attn_mask,
                                                  key_padding_mask=key_padding_mask,
                                                  training=self.training)

具体的 _multi_head_forward_attention 定义为

    def _multi_head_forward_attention(self,
                                      query,
                                      key,
                                      value,
                                      dropout_p,
                                      attn_mask=None,
                                      key_padding_mask=None,
                                      training=True):
        ############################
        # 第一阶段: 计算投影后的Q, K, V
        ############################
        q = self.q_proj(query)  # (n, N, embed_dim)
        k = self.k_proj(key)  # (m, N, embed_dim)
        v = self.v_proj(value)  # (m, N, embed_dim)

        ############################
        # 第二阶段: attn_mask的维度检查
        ############################
        n, N, embed_dim = q.size()
        m = key.size(0)
        if attn_mask is not None:
            if attn_mask.dim() == 2:
                if attn_mask.shape != (n, m):
                    raise RuntimeError
                attn_mask = attn_mask.unsqueeze(0)
            elif attn_mask.dim() == 3:
                if attn_mask.shape != (self.num_heads * N, n, m):
                    raise RuntimeError
            else:
                raise RuntimeError

        ##########################################
        # 第三阶段: 将attn_mask和key_padding_mask合并
        ##########################################
        if key_padding_mask is not None:
            assert key_padding_mask.shape == (N, m)
            key_padding_mask = key_padding_mask.view(N, 1, 1, m).expand(-1, self.num_heads, -1,
                                                                        -1).reshape(self.num_heads * N, 1, m)
            if attn_mask is None:
                attn_mask = key_padding_mask
            elif attn_mask.dtype == torch.bool:
                attn_mask = attn_mask.logical_or(key_padding_mask)
            else:
                attn_mask = attn_mask.masked_fill(key_padding_mask, -1e9)  # 为了防止出现nan，使用充分小的负数

        # 将attn_mask转换成浮点型张量
        if attn_mask is not None and attn_mask.dtype == torch.bool:
            new_attn_mask = torch.zeros_like(attn_mask, dtype=q.dtype)
            new_attn_mask.masked_fill_(attn_mask, -1e9)
            attn_mask = new_attn_mask

        ###################
        # 第四阶段: 计算注意力
        ###################
        # 将多头注意力化简为高维单头注意力
        q = q.reshape(n, N * self.num_heads, self.head_dim).transpose(0, 1)  # (N * num_heads, n, head_dim)
        k = k.reshape(m, N * self.num_heads, self.head_dim).transpose(0, 1)  # (N * num_heads, m, head_dim)
        v = v.reshape(m, N * self.num_heads, self.head_dim).transpose(0, 1)  # (N * num_heads, m, head_dim)

        if not training:
            dropout_p = 0.0

        attn_output, attn_output_weights = self._scaled_dot_product_attention(q, k, v, attn_mask, dropout_p)
        # 截至目前，attn_output: (N * num_heads, n, head_dim), attn_output_weights: (N * num_heads, n, m)
        attn_output = attn_output.transpose(0, 1).reshape(n, N, embed_dim)  # 合并num_heads个头的结果
        attn_output = self.out_proj(attn_output)
        attn_output_weights = attn_output_weights.reshape(N, self.num_heads, n, m)
        return attn_output, attn_output_weights

4.1 两种mask的理解

多头注意力机制中最重要的两个mask要属 key_padding_mask 和 attn_mask 了，彻底掌握这两个mask有助于理解代码。

4.1.1 key_padding_mask

假设现在有一批句子，形状为 $(N=2,L=5)$

[
    ['a', 'b', 'c', '', ''],
    ['x', 'y', '', '', ''],
]

例如对于第一个句子，a 作为query时，会看到四种词元：a 本身，b，c 和填充词元 。显然 a 与 之间进行计算毫无意义，因此需要用 key_padding_mask 来遮住这些填充词元，第二个句子同理，具体操作如下

[
    [False, False, False, True, True],
    [False, False, True, True, True],
]

那么 key_padding_mask 具体是怎样运作的呢？以第一个句子为例，进行self-attention计算时，$Q,K,V$ 的形状均为 $(5,d_{\text{model}})$，无论是 $Q$ 还是 $K$，每一行都对应了一个词元的embedding。而 key_padding_mask 遮住的是后两个词元，因此 $K$ 的最后两行会被替换成 $-\infty$，即 $K^{\text{T}}$ 的最后两列会被替换成 $-\infty$，所以 $Q{K}^{\text{T}}$ 的最后两列也是 $-\infty$，经过softmax后得到的注意力权重矩阵的最后两列是 $0$，这样一来，$V$ 的最后两行会被忽略，即只有未被遮蔽的词元才会被注意到。

需要注意的是，我们只对 $K$ 进行了mask，而填充词元不仅会作为key，也会作为query，依然以第一个句子为例，$Q{K}^{\text{T}}$ 的最后两行实际上就是填充词元作为query时与其他词元进行注意力计算得到的结果，而这种结果也是没有意义的，所以需要在loss中指定 ignore_index=padding_idx。

截至目前我们可以对 key_padding_mask 做一个简单总结：首先它是一个布尔型张量，其次它只遮盖 $K$，或者说它遮盖注意力分数 $Q{K}^{\text{T}}$（进行softmax前叫分数，softmax后叫权重）。

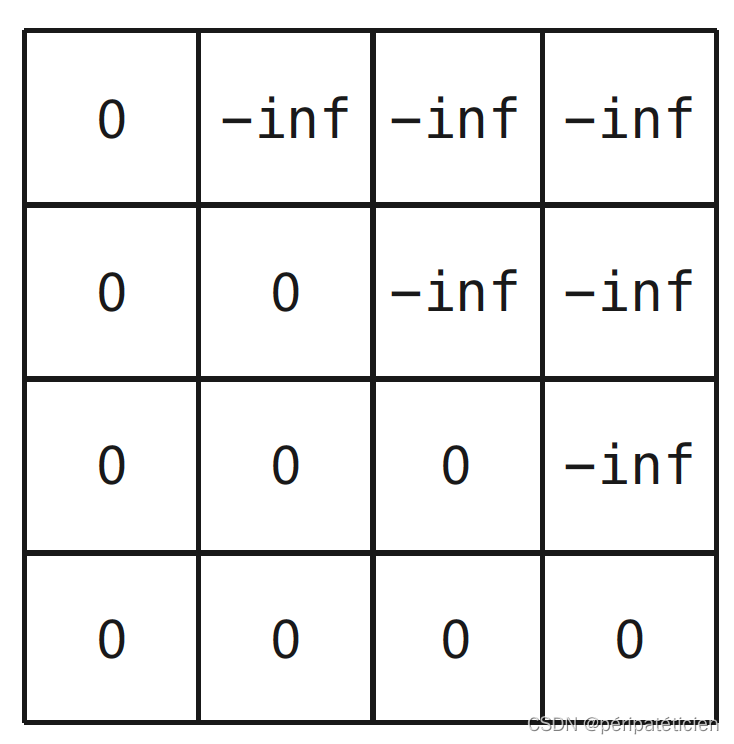
4.1.2 attn_mask

在用RNN构成的解码器中，我们是逐时间步进行输出的，而在自注意力机制中，无论位于哪个时间步都可以一次性看到所有时间步的信息，这显然不符合常识，因为当前时间步不能看到之后时间步的信息，所以需要对当前时间步之后的位置进行mask：

具体来讲，单词 “am” 作为查询时，它与 “very” 和 “happy” 之间的注意力权重应均为0，即 “am” 只能注意到 “I” 和 “am” 自己。由于 “am” 是序列的第二个词元，因此 “am” 对应的是注意力权重矩阵的第二行，该行一共有4个元素，分别是 “am” 与 “I”、“am”、“very”、“happy” 之间的注意力权重，所以该行的最后两个元素应均为0。因为注意力权重是由注意力分数 $Q{K}^{\text{T}}$ 经过softmax得来，所以 $Q{K}^{\text{T}}$ 的第二行的最后两个元素应当为 $-\infty$。同理可得，$Q{K}^{\text{T}}$ 第一行的最后三个元素，第三行的最后一个元素都为 $-\infty$，因此 attn_mask 是一个上三角矩阵，如下：

使用时只需要将 attn_mask 直接加到 $Q{K}^{\text{T}}$ 上即可。

截至目前我们可以对 attn_mask 做一个简单总结：它可以是布尔型张量也可以是浮点型张量，如果属于前者，则先转化成后者再使用，attn_mask 只遮盖 $Q{K}^{\text{T}}$ 的上三角部分。

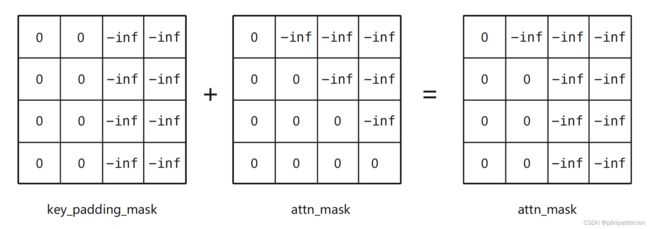
4.2 合并两种mask

可以看出，key_padding_mask 遮盖的是 $Q{K}^{\text{T}}$ 的最后几列，而 attn_mask 遮盖的是 $Q{K}^{\text{T}}$ 的上三角部分，它们遮盖的对象都是 $Q{K}^{\text{T}}$，因此我们完全可以将两种mask合并起来再进行遮盖。

具体而言，key_padding_mask 是一定存在的，因为一定会有 词元，但 attn_mask 不一定存在，比如Transformer的Encoder部分就不需要做 attn_mask。

如果 attn_mask 不存在，我们就令 attn_mask=key_padding_mask，如果 attn_mask 存在，我们就将 attn_mask 与 key_padding_mask 合并起来作为新的 attn_mask，这样一来，我们只需要关注 attn_mask 就行了。

两种mask的合并过程如下（一个可能的例子）：

沿用PyTorch官方文档的记号，key_padding_mask 的形状为 $(N,S)$，attn_mask 的形状通常为 $(N\cdot \text{num\_heads},L,S)$，两者形状不同无法直接合并，所以需要对 key_padding_mask 的形状进行变换：

$$(N,S)\to (N,1,1,S)\to (N,\text{num\_heads},1,S)\to (N\cdot \text{num\_heads},1,S)$$

第二个箭头代表复制操作，具体请见之前的代码。

4.3 MHA完整代码

class MultiHeadAttention(nn.Module):
    def __init__(self, embed_dim, num_heads, dropout=0.0, bias=True):
        super().__init__()
        self.embed_dim = embed_dim
        self.num_heads = num_heads
        self.head_dim = embed_dim // num_heads
        self.dropout = dropout
        assert self.head_dim * num_heads == embed_dim

        self.q_proj = nn.Linear(embed_dim, embed_dim, bias=bias)
        self.k_proj = nn.Linear(embed_dim, embed_dim, bias=bias)
        self.v_proj = nn.Linear(embed_dim, embed_dim, bias=bias)
        self.out_proj = nn.Linear(embed_dim, embed_dim, bias=bias)

    def forward(self, query, key, value, attn_mask=None, key_padding_mask=None):
        """
        Args:
            query: (n, N, embed_dim)
            key: (m, N, embed_dim)
            value: (m, N, embed_dim)
            attn_mask (bool Tensor or float Tensor): (n, m) or (N * num_heads, n, m)
            key_padding_mask (bool Tensor): (N, m)

        Returns:
            attn_output: (n, N, embed_dim)
            attn_output_weights: (N, num_heads, n, m)
        """
        return self._multi_head_forward_attention(query,
                                                  key,
                                                  value,
                                                  dropout_p=self.dropout,
                                                  attn_mask=attn_mask,
                                                  key_padding_mask=key_padding_mask,
                                                  training=self.training)

    def _multi_head_forward_attention(self, query, key, value, dropout_p, attn_mask=None, key_padding_mask=None, training=True):
        q, k, v = self.q_proj(query), self.k_proj(key), self.v_proj(value)
        n, N, embed_dim = q.size()
        m = key.size(0)

        if attn_mask is not None:
            if attn_mask.dim() == 2:
                assert attn_mask.shape == (n, m)
                attn_mask = attn_mask.unsqueeze(0)
            elif attn_mask.dim() == 3:
                assert attn_mask.shape == (N * self.num_heads, n, m)
            else:
                raise RuntimeError

        if key_padding_mask is not None:
            assert key_padding_mask.shape == (N, m)
            key_padding_mask = key_padding_mask.view(N, 1, 1, m).repeat(1, self.num_heads, 1, 1).reshape(N * self.num_heads, 1, m)
            if attn_mask is None:
                attn_mask = key_padding_mask
            elif attn_mask.dtype == torch.bool:
                attn_mask = attn_mask.logical_or(key_padding_mask)
            else:
                attn_mask = attn_mask.masked_fill(key_padding_mask, -1e9)

        if attn_mask is not None and attn_mask.dtype == torch.bool:
            new_attn_mask = torch.zeros_like(attn_mask, dtype=q.dtype)
            new_attn_mask.masked_fill_(attn_mask, -1e9)
            attn_mask = new_attn_mask

        q = q.reshape(n, N * self.num_heads, self.head_dim).transpose(0, 1)
        k = k.reshape(m, N * self.num_heads, self.head_dim).transpose(0, 1)
        v = v.reshape(m, N * self.num_heads, self.head_dim).transpose(0, 1)

        if not training:
            dropout_p = 0.0

        attn_output, attn_output_weights = self._scaled_dot_product_attention(q, k, v, attn_mask, dropout_p)
        attn_output = attn_output.transpose(0, 1).reshape(n, N, embed_dim)
        attn_output = self.out_proj(attn_output)
        attn_output_weights = attn_output_weights.reshape(N, self.num_heads, n, m)
        return attn_output, attn_output_weights

    def _scaled_dot_product_attention(self, q, k, v, attn_mask=None, dropout_p=0.0):
        """
        Args:
            q: (N, n, E), where E is embedding dimension.
            k: (N, m, E)
            v: (N, m, E)
            attn_mask: (n, m) or (N, n, m)
        
        Returns:
            attn_output: (N, n, E)
            attn_weights: (N, n, m)
        """
        q = q / math.sqrt(q.size(2))
        if attn_mask is not None:
            scores = q @ k.transpose(-2, -1) + attn_mask
        else:
            scores = q @ k.transpose(-2, -1)

        attn_weights = F.softmax(scores, dim=-1)
        if dropout_p > 0.0:
            attn_weights = F.dropout(attn_weights, p=dropout_p)
        attn_output = attn_weights @ v
        return attn_output, attn_weights

4.4 多头自注意力

多头自注意力的 query, key 和 value 都是序列本身，实现非常简单

class MultiHeadSelfAttention(nn.Module):
    def __init__(self, embed_dim, num_heads, dropout=0.0, bias=True):
        super().__init__()
        self.mha = MultiHeadAttention(embed_dim, num_heads, dropout=dropout, bias=bias)

    def forward(self, X, attn_mask=None, key_padding_mask=None):
        """
        Args:
            X (input sequence): (L, N, embed_dim), where L is sequence length.
        """
        return self.mha(X, X, X, attn_mask=attn_mask, key_padding_mask=key_padding_mask)

---

⚠️ 由于博主水平有限，文章难免存在不当甚至是错误之处，欢迎在评论区指出。
完整代码请前往 attention-pytorch 进行查看。码文不易，下载时还请您随手给一个follow和star，谢谢！

---

References

[1] https://zhuanlan.zhihu.com/p/366592542
[2] https://zzxn.github.io/2020/11/03/multihead-attention-in-pytorch.html
[3] https://www.zhihu.com/column/nulls
[4] https://cloud.tencent.com/developer/article/1810411
[5] https://pytorch.org/docs/stable/generated/torch.nn.MultiheadAttention.html#torch.nn.MultiheadAttention