K－近邻实现（K_Nearest_Neighbor）

目录

 1、引言

2、K近邻法

2.1 Matlab实现

        主函数

        Loss函数

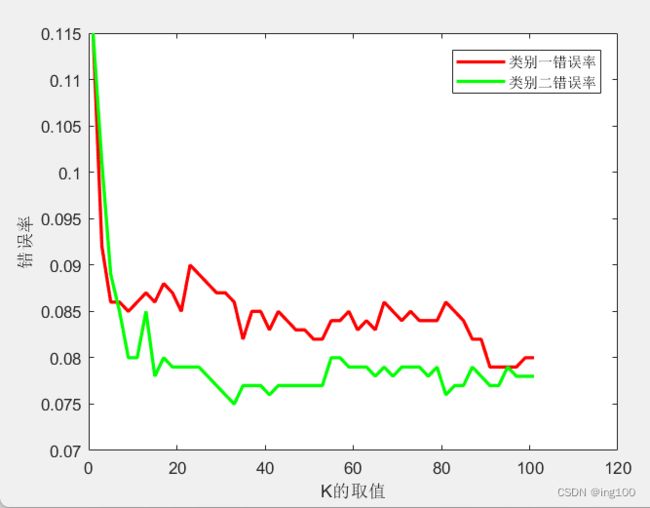
附上效果图

2.2、Python实现

2.3、C++实现

main函数

Loss函数

---

 1、引言

        本专栏会编程实现机器学习的一些经典算法并且使用三种不同语言（Matlab,python,c++）。本文只展示了部分代码，本专栏全部代码可以通过Github下载，这里里简述一下为什么是这三种语言吧，

        首先是Matlab：这是大多数理工科学生都会用到的一个软件，仿真与分析计算的黑科技，从2022年开始matlab不断更新有关AI的工具包个人猜测以后会成为很多本科生和研究生的研究AI的工具

        然后是python：目前最流行的AI以及数据分析的语言，其语法与matlab及其类似，外部库非常丰富，本文主要使用pytorch以及numpy这两个库进行实现

        最后是C++：目前很多python有关深度学习的库都有C++的版本，比如pytotch->libtorch  numpy->numcpp   opencv-python->opencv等等。因为python的底层就是用C或者C++编写的所以C++的运行速度会比python快很多，个人觉得一个项目最后都最好使用C++落地，而专栏主要使用libtorch以及numcpp进行实现。

2、K近邻法

正题开始，本专栏的第一个算法就是K近邻法。

        在介绍之前先说一下最近邻法：常用于分类，以二分类为例，给定一些训练样本分为A类和B类以及一个测试样本然后找到测试样本离训练样本最近的一个点，查看这个点属于什么类别就作为测试样本的类别。

        最近邻法就是K＝1时的K近邻法，所以K近邻就是找到K个（K都是人为定义的一个数）距离训练样本最近的点，判断在K个点中哪种类别的数量更多。为了防止在K个点中A类与B类的数量一样多，所以K的取值一般为奇数（1，3，5等等）

        之后的代码都会完成这几个任务（三种代码逻辑完全一致）

        （1）使用随机函数生成10000个随机样本，共两类，每类5000个，其中每类中4000个为训练集，1000个为测试集。作为后续程序的数据基础。

        （2）编写k近邻法程序，实现对两类共2000个测试样本的近邻法判别。
        （3）统计1、3、5、7.....、101时的测试错误率，绘制错误率曲线。

2.1 Matlab实现

        主函数

clc;clear all;close all   % 清理
%% 制定训练集 
% 使用randn函数产生均值为0，方差σ^2 = 1，标准差σ=1的正态分布的随机矩阵，2000个数据，分两类。
X = [randn(5000,2)+ones(5000,2);randn(5000,2)-ones(5000,2)];
X(1:5000,3)=1;
X(5001:10000,3)=2;
% 划分训练集以及测试集
% 对于类别一 1-4000为训练集 4001－5000为测试集
% 对于类别二 5001－9000为训练集 9001－10000为测试集 
class1_train = X(1:4000,:);
class1_test = X(4001:5000,:);
class2_train = X(5001:9000,:);
class2_test = X(9001:10000,:);

%% 绘图
figure
plot(class1_train(:,1),class1_train(:,2),'r*'); hold on;
plot(class2_train(:,1),class2_train(:,2),'b*');
grid on;
legend({'class2train','class2test'},'Location','northwest')   
%% 存储
%save ('NN_2000.mat','X');
%frame = getframe(fig); % 获取frame
%img = frame2im(frame); % 将frame变换成imwrite函数可以识别的格式
%imwrite(img,'a.png');
%% 开始运行K近邻 K从1到101步长为2
total_Kcorrect1 = [];
for i=1:2:101
    [num_correct1] = Loss(class1_train,class2_train,class1_test,i);
    total_Kcorrect1 = [total_Kcorrect1;num_correct1];
end

total_Kcorrect2 = [];
for j=1:2:101
    [num_correct2] = Loss(class1_train,class2_train,class2_test,j);
    total_Kcorrect2 = [total_Kcorrect2;num_correct2];
end
%% 统计结果
figure
x = linspace(1,101,51);
plot(x,1-total_Kcorrect1/1000,'r','LineWidth',2)
hold on
plot(x,1-total_Kcorrect2/1000,'g','LineWidth',2)

legend({'类别一错误率','类别二错误率'})

        Loss函数

function [correct_num] = Loss(class1,class2,test,k)
    x = size(test,1);  % test数据集有多少行
    num1=0;
    num2=0;
    correct_num=0;
    distance = [];
    for i=1:x
        % 开始计算单个测试数据与其它8000个训练集的距离
        distance1 = sqrt( (class1(:,1)-test(i,1)).^2 + (class1(:,2)-test(i,2)).^2 );
        %distance = [distance;distance1];
        distance2 = sqrt( (class2(:,1)-test(i,1)).^2 + (class2(:,2)-test(i,2)).^2 );
        distance = [distance1;distance2];
        % 进行逆序排列取前k个
        [~,index] = sortrows(distance);
        for j=1:k
           if index(j,1) < 4000
               num1 = num1 +1;
               
           elseif index(j,1) > 4000
               num2 = num2 + 1;
           end
        end
        if num1 > num2
            if test(i,3) == 1
                correct_num = correct_num + 1;
            end
        elseif num1 < num2
            if test(i,3) == 2
                correct_num = correct_num + 1;
            end
        end
        num1 = 0;
        num2 = 0;
    end
end

附上效果图

2.2、Python实现

python实现会使用到深度学习框架pytorch因其可以使用GPU加速运算，若读者感兴趣也可以使用numpy实现（难度不高，pytorch对数组的操作numpy基本都有）

main函数

if __name__ == "__main__":
    ## 定义数据集
    device = torch.device('cuda' if torch.cuda.is_available else 'cpu')
    X1 = torch.randn(5000, 2) + torch.ones(5000, 2)
    X2 = torch.randn(5000, 2) - torch.ones(5000, 2)
    X = torch.cat((X1, X2), 0, )  # (10000,2)
    label = torch.IntTensor(10000, 1)
    label[:5000] = 1
    label[5000:] = 2
    Data_set = torch.cat((X, label), 1)
    # Data_set = Data_set.cuda()
    class1_train = Data_set[:4000, :]
    # print(class1_train.device)
    class1_test = Data_set[4000:5000, :]
    class2_train = Data_set[5000:9000, :]
    class2_test = Data_set[9000:, :]
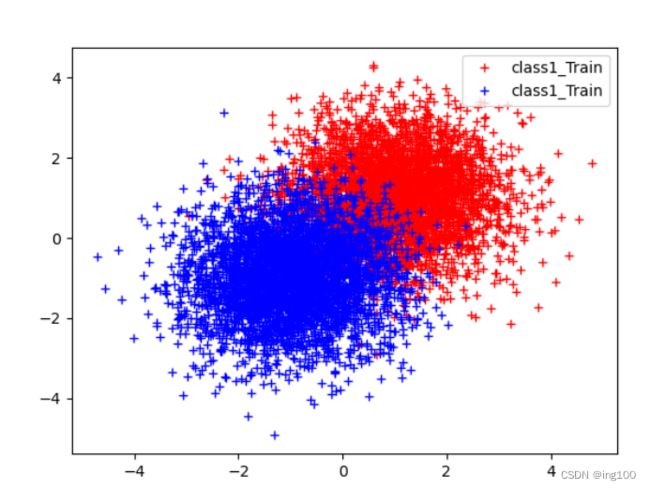
    ## 绘制数据集
    plt.plot(class1_train[:, 0], class1_train[:, 1], 'r+', label="class1_Train")
    plt.plot(class2_train[:, 0], class2_train[:, 1], 'b+', label="class1_Train")
    plt.legend(loc='upper right')
    plt.show()
    ## 开始训练
    total_Kcorrect1 = []
    for num_k in range(1, 11, 2):
        num_correct = Loss(class1_train, class2_train, class1_test, num_k)
        total_Kcorrect1.append(num_correct)

    total_Kcorrect2 = []
    for num_k in range(1, 11, 2):
        num_correct = Loss(class1_train, class2_train, class2_test, num_k)
        total_Kcorrect2.append(num_correct)

    total_Kcorrect2 = list(map(lambda x : float(1-x/1000), total_Kcorrect2))
    total_Kcorrect1 = list(map(lambda x : float(1-x/1000), total_Kcorrect1))
    plt.figure()
    x = range(1, 11, 2)
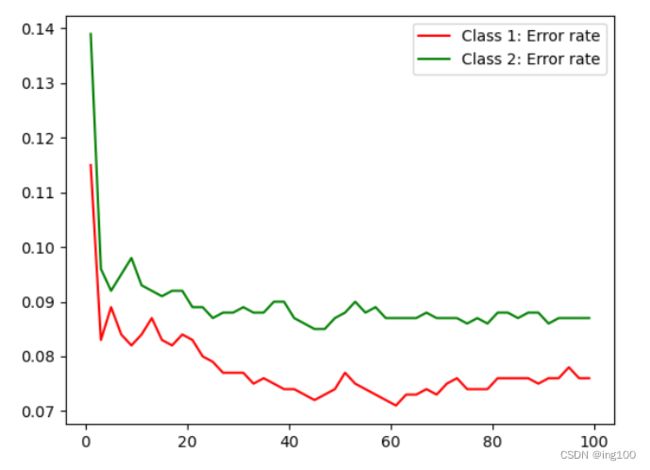
    plt.plot(x, total_Kcorrect1[:], 'r-', label='Class 1: Error rate')
    plt.plot(x, total_Kcorrect2[:], 'g-', label='Class 2: Error rate')
    plt.legend()
    plt.show()

Loss函数

def Loss(class1,class2,test,k):
    x = test.shape
    correct_num = 0
    distance = torch.Tensor([]).cuda()
    # distance = torch.Tensor([])
    print(distance.device)
    for i in range(0, x[0]):
        num1 = 0
        num2 = 0
        distance1 = torch.sqrt( torch.square(class1[:, 0]-test[i, 0]) + torch.square(class1[:, 1]-test[i, 1]) )
        distance1.to(device)
        distance2 = torch.sqrt( torch.square(class2[:, 0]-test[i, 0]) + torch.square(class2[:, 1]-test[i, 1]) )
        distance2.to(device)
        distance = torch.cat((distance1,distance2), 0)
        _, index = torch.sort(distance, 0)
        for j in range(0, k):
            if index[j] <= 4000:
                num1 = num1 + 1
            elif index[j] > 4000:
                num2 = num2 + 1
        if num1 > num2 and test[i, 2] == 1:
            correct_num = correct_num + 1
        elif num1 < num2 and test[i, 2] == 2:
            correct_num = correct_num + 1
    return correct_num

效果展示

2.3、C++实现

C++会使用到使Libtorch库（pytorch的C++版本），同样若读者感兴趣也可以使用numcpp实现，安装方法这里不多介绍以下为代码

main函数

void main()
{
	vector total_Kcorrect1;
	vector total_Kcorrect2;
	int num_correct = 0;
	torch::Tensor X1 = torch::randn({ 5000,2 }) + torch::ones({ 5000,2 });
	torch::Tensor X2 = torch::randn({ 5000,2 }) - torch::ones({ 5000,2 });
	torch::Tensor X = torch::cat({ X1, X2 }, 0);
	torch::Tensor label1 = torch::full({ 5000,1 },1);
	torch::Tensor label2 = torch::full({ 5000,1 }, 2);
	torch::Tensor label = torch::cat({ label1, label2 }, 0);
	torch::Tensor data_set = torch::cat({ X,label }, 1).to(device_type);  // GPU   CUDA0
	// cout << data_set.device() << endl;
	// 划分训练集以及测试集
	auto class1_train = data_set.narrow(0, 0, 4000);
	auto class1_test = data_set.narrow(0, 4000, 1000);
	auto class2_train = data_set.narrow(0, 5000, 4000);
	auto class2_test = data_set.narrow(0, 9000, 1000);
	

	for (int m1 = 1; m1 <= 101; m1 = m1 + 2)
	{
		num_correct = Loss(class1_train, class2_train, class1_test, m1);
		total_Kcorrect1.push_back(num_correct);
	}
	for (int m2 = 0; m2 < 101; m2 = m2 + 2)
	{
		num_correct = Loss(class1_train, class2_train, class1_test, m2);
		total_Kcorrect2.push_back(num_correct);
	}
	for (int k = 0; k < total_Kcorrect1.size(); k++)
	{
		cout << total_Kcorrect1[k] << "  ";
	}

}

Loss函数

long Loss(torch::Tensor class1, torch::Tensor class2, torch::Tensor test,int k)
{
	c10::IntArrayRef tsize = test.sizes();
	int num1 = 0;
	int num2 = 0;
	int correct_num = 0;
	auto distance = torch::tensor({ }).to(device_type);
	cout << distance.device() << endl;
	for (long i = 0; i < tsize[0]; i++)
	{
		auto distance1 = torch::sqrt(torch::square(class1.narrow(1, 0, 1) - test[i][0]) + torch::square(class1.narrow(1, 1, 1) - test[i][1])).to(device_type);
		auto distance2 = torch::sqrt(torch::square(class2.narrow(1, 0, 1) - test[i][0]) + torch::square(class2.narrow(1, 1, 1) - test[i][1])).to(device_type);
		auto distance = torch::cat({ distance1, distance2 }, 0);
		tuple sort_ret = torch::sort(distance, 0, 0);    // {8000,1}

		//cout << distance << endl;
		
		for (int j = 0; j < k; j++)
		{
			int a = (get<1>(sort_ret)[j][0]).item();
			if (a <= 4000)
			{
				num1 += 1;
			}
			else if (a > 4000)
			{
				num2 += 1;
			}
		}
		if (num1 > num2 && test[i][2].item() == 1)
		{
			correct_num += 1;
		}
		else if (num1 < num2 && test[i][2].item() == 2)
		{
			correct_num += 1;
		}
		num1 = 0;
		num2 = 0;
	}
	return correct_num;
}