python 多组直方图 画图_5种方法教你用Python玩转histogram直方图
直方图是一个可以快速展示数据概率分布的工具,直观易于理解,并深受数据爱好者的喜爱。大家平时可能见到最多就是matplotlib,seaborn等高级封装的库包,类似以下这样的绘图。
本篇博主将要总结一下使用Python绘制直方图的所有方法,大致可分为三大类(详细划分是五类,参照文末总结):纯Python实现直方图,不使用任何第三方库
使用Numpy来创建直方图总结数据
使用matplotlib,pandas,seaborn绘制直方图
下面,我们来逐一介绍每种方法的来龙去脉。
纯Python实现histogram
当准备用纯Python来绘制直方图的时候,最简单的想法就是将每个值出现的次数以报告形式展示。这种情况下,使用字典来完成这个任务是非常合适的,我们看看下面代码是如何实现的。>>> a = (0, 1, 1, 1, 2, 3, 7, 7, 23)
>>> def count_elements(seq) -> dict:
... """Tally elements from `seq`."""
... hist = {}
... for i in seq:
... hist[i] = hist.get(i, 0) + 1
... return hist
>>> counted = count_elements(a)
>>> counted
{0: 1, 1: 3, 2: 1, 3: 1, 7: 2, 23: 1}
我们看到,count_elements()返回了一个字典,字典里出现的键为目标列表里面的所有唯一数值,而值为所有数值出现的频率次数。hist[i] = hist.get(i, 0) + 1实现了每个数值次数的累积,每次加一。
实际上,这个功能可以用一个Python的标准库collection.Counter类来完成,它兼容Pyhont 字典并覆盖了字典的.update()方法。
>>> from collections import Counter
>>> recounted = Counter(a)
>>> recounted
Counter({0: 1, 1: 3, 3: 1, 2: 1, 7: 2, 23: 1})
可以看到这个方法和前面我们自己实现的方法结果是一样的,我们也可以通过collection.Counter来检验两种方法得到的结果是否相等。>>> recounted.items() == counted.items()
True
我们利用上面的函数重新再造一个轮子ASCII_histogram,并最终通过Python的输出格式format来实现直方图的展示,代码如下:def ascii_histogram(seq) -> None:
"""A horizontal frequency-table/histogram plot."""
counted = count_elements(seq)
for k in sorted(counted):
print('{0:5d} {1}'.format(k, '+' * counted[k]))
这个函数按照数值大小顺序进行绘图,数值出现次数用(+)符号表示。在字典上调用sorted()将会返回一个按键顺序排列的列表,然后就可以获取相应的次数counted[k]。>>> import random
>>> random.seed(1)
>>> vals = [1, 3, 4, 6, 8, 9, 10]
>>> # `vals` 里面的数字将会出现5到15次
>>> freq = (random.randint(5, 15) for _ in vals)
>>> data = []
>>> for f, v in zip(freq, vals):
... data.extend([v] * f)
>>> ascii_histogram(data)
1 +++++++
3 ++++++++++++++
4 ++++++
6 +++++++++
8 ++++++
9 ++++++++++++
10 ++++++++++++
这个代码中,vals内的数值是不重复的,并且每个数值出现的频数是由我们自己定义的,在5和15之间随机选择。然后运用我们上面封装的函数,就得到了纯Python版本的直方图展示。
总结:纯python实现频数表(非标准直方图),可直接使用collection.Counter方法实现。
使用Numpy实现histogram
以上是使用纯Python来完成的简单直方图,但是从数学意义上来看,直方图是分箱到频数的一种映射,它可以用来估计变量的概率密度函数的。而上面纯Python实现版本只是单纯的频数统计,不是真正意义上的直方图。
因此,我们从上面实现的简单直方图继续往下进行升级。一个真正的直方图首先应该是将变量分区域(箱)的,也就是分成不同的区间范围,然后对每个区间内的观测值数量进行计数。恰巧,Numpy的直方图方法就可以做到这点,不仅仅如此,它也是后面将要提到的matplotlib和pandas使用的基础。
举个例子,来看一组从拉普拉斯分布上提取出来的浮点型样本数据。这个分布比标准正态分布拥有更宽的尾部,并有两个描述参数(location和scale):
>>> import numpy as np
>>> np.random.seed(444)
>>> np.set_printoptions(precision=3)
>>> d = np.random.laplace(loc=15, scale=3, size=500)
>>> d[:5]
array([18.406, 18.087, 16.004, 16.221, 7.358])
由于这是一个连续型的分布,对于每个单独的浮点值(即所有的无数个小数位置)并不能做很好的标签(因为点实在太多了)。但是,你可以将数据做分箱处理,然后统计每个箱内观察值的数量,这就是真正的直方图所要做的工作。
下面我们看看是如何用Numpy来实现直方图频数统计的。
>>> hist, bin_edges = np.histogram(d)
>>> hist
array([ 1, 0, 3, 4, 4, 10, 13, 9, 2, 4])
>>> bin_edges
array([ 3.217, 5.199, 7.181, 9.163, 11.145, 13.127, 15.109, 17.091,
19.073, 21.055, 23.037])
这个结果可能不是很直观。来说一下,np.histogram()默认地使用10个相同大小的区间(箱),然后返回一个元组(频数,分箱的边界),如上所示。要注意的是:这个边界的数量是要比分箱数多一个的,可以简单通过下面代码证实。>>> hist.size, bin_edges.size
(10, 11)
那问题来了,Numpy到底是如何进行分箱的呢?只是通过简单的 np.histogram()就可以完成了,但具体是如何实现的我们仍然全然不知。下面让我们来将 np.histogram()的内部进行解剖,看看到底是如何实现的(以最前面提到的a列表为例)。>>> # 取a的最小值和最大值
>>> first_edge, last_edge = a.min(), a.max()
>>> n_equal_bins = 10 # NumPy得默认设置,10个分箱
>>> bin_edges = np.linspace(start=first_edge, stop=last_edge,
... num=n_equal_bins + 1, endpoint=True)
...
>>> bin_edges
array([ 0. , 2.3, 4.6, 6.9, 9.2, 11.5, 13.8, 16.1, 18.4, 20.7, 23. ])
解释一下:首先获取a列表的最小值和最大值,然后设置默认的分箱数量,最后使用Numpy的linspace方法进行数据段分割。分箱区间的结果也正好与实际吻合,0到23均等分为10份,23/10,那么每份宽度为2.3。
除了np.histogram之外,还存在其它两种可以达到同样功能的方法:np.bincount()和np.searchsorted(),下面看看代码以及比较结果。>>> bcounts = np.bincount(a)
>>> hist, _ = np.histogram(a, range=(0, a.max()), bins=a.max() + 1)
>>> np.array_equal(hist, bcounts)
True
>>> # Reproducing `collections.Counter`
>>> dict(zip(np.unique(a), bcounts[bcounts.nonzero()]))
{0: 1, 1: 3, 2: 1, 3: 1, 7: 2, 23: 1}
总结:通过Numpy实现直方图,可直接使用np.histogram()或者np.bincount()。
使用Matplotlib和Pandas可视化Histogram
从上面的学习,我们看到了如何使用Python的基础工具搭建一个直方图,下面我们来看看如何使用更为强大的Python库包来完成直方图。Matplotlib基于Numpy的histogram进行了多样化的封装并提供了更加完善的可视化功能。
import matplotlib.pyplot as plt
# matplotlib.axes.Axes.hist() 方法的接口
n, bins, patches = plt.hist(x=d, bins='auto', color='#0504aa',
alpha=0.7, rwidth=0.85)
plt.grid(axis='y', alpha=0.75)
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.title('My Very Own Histogram')
plt.text(23, 45, r'$\mu=15, b=3$')
maxfreq = n.max()
# 设置y轴的上限
plt.ylim(ymax=np.ceil(maxfreq / 10) * 10 if maxfreq % 10 else maxfreq + 10)
之前我们的做法是,在x轴上定义了分箱边界,y轴是相对应的频数,不难发现我们都是手动定义了分箱的数目。但是在以上的高级方法中,我们可以通过设置bins='auto'自动在写好的两个算法中择优选择并最终算出最适合的分箱数。这里,算法的目的就是选择出一个合适的区间(箱)宽度,并生成一个最能代表数据的直方图来。
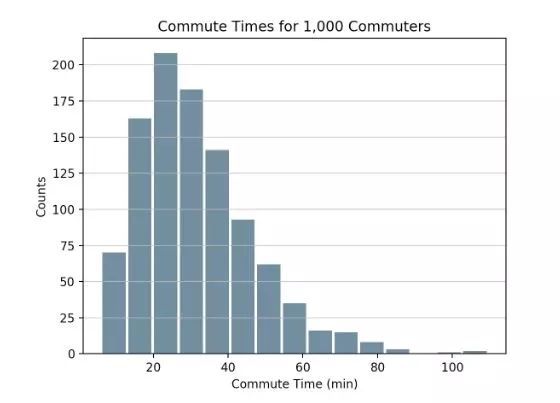
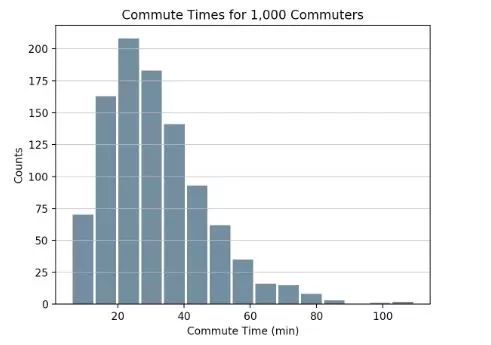
如果使用Python的科学计算工具实现,那么可以使用Pandas的Series.histogram(),并通过matplotlib.pyplot.hist()来绘制输入Series的直方图,如下代码所示。import pandas as pd
size, scale = 1000, 10
commutes = pd.Series(np.random.gamma(scale, size=size) ** 1.5)
commutes.plot.hist(grid=True, bins=20, rwidth=0.9,
color='#607c8e')
plt.title('Commute Times for 1,000 Commuters')
plt.xlabel('Counts')
plt.ylabel('Commute Time')
plt.grid(axis='y', alpha=0.75)
pandas.DataFrame.histogram()的用法与Series是一样的,但生成的是对DataFrame数据中的每一列的直方图。
总结:通过pandas实现直方图,可使用Seris.plot.hist(),DataFrame.plot.hist(),matplotlib实现直方图可以用matplotlib.pyplot.hist()。
绘制核密度估计(KDE)
KDE(Kernel density estimation)是核密度估计的意思,它用来估计随机变量的概率密度函数,可以将数据变得更平缓。
使用Pandas库的话,你可以使用plot.kde()创建一个核密度的绘图,plot.kde() 对于 Series和DataFrame数据结构都适用。但是首先,我们先生成两个不同的数据样本作为比较(两个正太分布的样本):
>>> # 两个正太分布的样本
>>> means = 10, 20
>>> stdevs = 4, 2
>>> dist = pd.DataFrame(
... np.random.normal(loc=means, scale=stdevs, size=(1000, 2)),
... columns=['a', 'b'])
>>> dist.agg(['min', 'max', 'mean', 'std']).round(decimals=2)
a b
min -1.57 12.46
max 25.32 26.44
mean 10.12 19.94
std 3.94 1.94
以上看到,我们生成了两组正态分布样本,并且通过一些描述性统计参数对两组数据进行了简单的对比。现在,我们可以在同一个Matplotlib轴上绘制每个直方图以及对应的kde,使用pandas的plot.kde()的好处就是:它会自动的将所有列的直方图和kde都显示出来,用起来非常方便,具体代码如下:fig, ax = plt.subplots()
dist.plot.kde(ax=ax, legend=False, title='Histogram: A vs. B')
dist.plot.hist(density=True, ax=ax)
ax.set_ylabel('Probability')
ax.grid(axis='y')
ax.set_facecolor('#d8dcd6')
总结:通过pandas实现kde图,可使用Seris.plot.kde(),DataFrame.plot.kde()。
使用Seaborn的完美替代
一个更高级可视化工具就是Seaborn,它是在matplotlib的基础上进一步封装的强大工具。对于直方图而言,Seaborn有 distplot() 方法,可以将单变量分布的直方图和kde同时绘制出来,而且使用及其方便,下面是实现代码(以上面生成的d为例):
import seaborn as sns
sns.set_style('darkgrid')
sns.distplot(d)
distplot方法默认的会绘制kde,并且该方法提供了fit参数,可以根据数据的实际情况自行选择一个特殊的分布来对应。
sns.distplot(d, fit=stats.laplace, kde=False)
 注意这两个图微小的区别。第一种情况你是在估计一个未知的概率密度函数(PDF),而第二种情况是你是知道分布的,并想知道哪些参数可以更好的描述数据。
注意这两个图微小的区别。第一种情况你是在估计一个未知的概率密度函数(PDF),而第二种情况是你是知道分布的,并想知道哪些参数可以更好的描述数据。
总结:通过seaborn实现直方图,可使用seaborn.distplot(),seaborn也有单独的kde绘图seaborn.kde()。
在Pandas中的其它工具
除了绘图工具外,pandas也提供了一个方便的.value_counts()方法,用来计算一个非空值的直方图,并将之转变成一个pandas的series结构,示例如下:
>>> import pandas as pd
>>> data = np.random.choice(np.arange(10), size=10000,
... p=np.linspace(1, 11, 10) / 60)
>>> s = pd.Series(data)
>>> s.value_counts()
9 1831
8 1624
7 1423
6 1323
5 1089
4 888
3 770
2 535
1 347
0 170
dtype: int64
>>> s.value_counts(normalize=True).head()
9 0.1831
8 0.1624
7 0.1423
6 0.1323
5 0.1089
dtype: float64
此外,pandas.cut()也同样是一个方便的方法,用来将数据进行强制的分箱。比如说,我们有一些人的年龄数据,并想把这些数据按年龄段进行分类,示例如下:>>> ages = pd.Series(
... [1, 1, 3, 5, 8, 10, 12, 15, 18, 18, 19, 20, 25, 30, 40, 51, 52])
>>> bins = (0, 10, 13, 18, 21, np.inf) # 边界
>>> labels = ('child', 'preteen', 'teen', 'military_age', 'adult')
>>> groups = pd.cut(ages, bins=bins, labels=labels)
>>> groups.value_counts()
child 6
adult 5
teen 3
military_age 2
preteen 1
dtype: int64
>>> pd.concat((ages, groups), axis=1).rename(columns={0: 'age', 1: 'group'})
age group
0 1 child
1 1 child
2 3 child
3 5 child
4 8 child
5 10 child
6 12 preteen
7 15 teen
8 18 teen
9 18 teen
10 19 military_age
11 20 military_age
12 25 adult
13 30 adult
14 40 adult
15 51 adult
16 52 adult
除了使用方便外,更加好的是这些操作最后都会使用Cython代码来完成,在运行速度的效果上也是非常快的。
总结:其它实现直方图的方法,可使用.value_counts()和pandas.cut()。
该使用哪个方法?
至此,我们了解了很多种方法来实现一个直方图。但是它们各自有什么有缺点呢?该如何对它们进行选择呢?当然,一个方法解决所有问题是不存在的,我们也需要根据实际情况而考虑如何选择,下面是对一些情况下使用方法的一个推荐,仅供参考。
你的情况推荐使用备注
有清晰的整数型数据在列表,元组,或者集合的数据结构中,并且你不想引入任何第三方那个库标准库Collection.counter()提供了快速直接的频数实现方法这只是频数的一个表,不存在histogram真正意义上的分箱
大的数组数据,并且你只是想要计算含有分箱的直方图(无可视化,纯数学计算)Numpy的np.histogram()和np.bincount()对于直方图的纯数学计算时非常有帮助的更多请查阅np.digitize()
数据存在于在Pandas的Series和DataFrame对象中Pandas方法,比如, Series.plot.hist(),DataFrame.plot.hist(),Series.value_counts(),and cut(),Series.plot.kde() 以及DataFrame.plot.kde()参考pandas的visualization章节
从任意数据结构中,创建一个高度定制化可调节的直方图推荐使用基于np.histogram()的Pyplot.hist()函数,被频繁使用,简单易懂。Matplotlib可定制化
提前封装的设计和集成(而非定制的)Seaborn的distplot(),可以方便的结合直方图和KDE绘图高级封装参考:https://realpython.com/python-histograms/