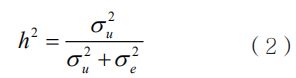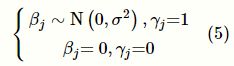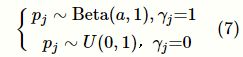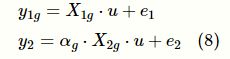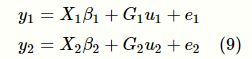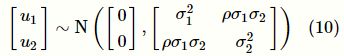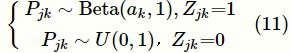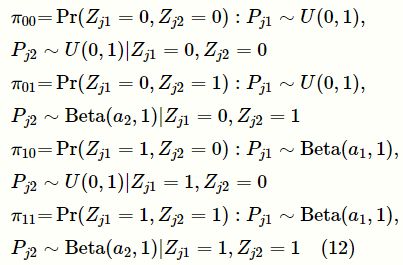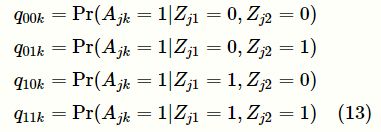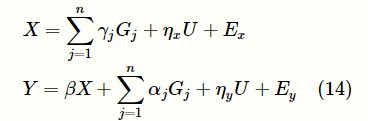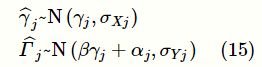基因大数据的集成分析

基因大数据的集成分析

胡湘红¹, 彭衡², 杨灿³, 张纵辉¹, 万翔¹, 罗智泉¹

1 深圳市大数据研究院，广东 深圳 518172

2 香港浸会大学数学系，香港 999077

3 香港科技大学数学系，香港 999077

摘要：随着生物科技（如基因芯片和测序技术）的飞速发展，全世界已经积累了海量的数据。有效地整合和集成多层面和多维度的基因大数据，对于全方位解析从遗传变异到疾病发生的整个因果链条具有关键作用，可为个性化、精准医疗服务奠定科学的基础。从3个方面对基因大数据的集成分析进行综述：检测风险位点及其功能分析、基因多效性的分析、基于孟德尔随机化的因果推断。进一步结合具体的应用案例进行了阐述，最后对基因大数据的集成分析研究进行了总结以及展望。

关键词：GWAS ; 集成分析 ; 多基因效应 ; 基因多效性 ; 孟德尔随机化

论文引用格式：

胡湘红, 彭衡, 杨灿, 张纵辉, 万翔, 罗智泉.基因大数据的集成分析. 大数据[J], 2019, 5(4):67-88

HU X H, PENG H, YANG C, ZHANG Z H, WAN X, LUO Z Q.Integrative analysis for big data in genomics. Big Data Research[J], 2019, 5(4):67-88

1 引言

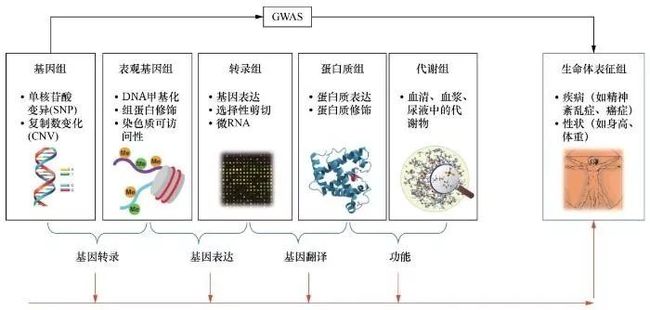
人类基因组计划（human genome project，HGP）以及人类遗传变异图谱在21世纪初宣告完成。这一里程碑式的事件拉开了大规模利用生物医疗数据研究复杂人类疾病的序幕。随着生物科技（如基因芯片和测序技术）的飞速发展，全世界的研究者已经积累了多层面、多维度的基因大数据。这些数据覆盖从遗传变异到生命体表征的各个层面的数据，包括基因组（genome）层面、表观基因组（epigenome）层面、转录组（transcriptome）层面、蛋白质组（proteome）层面、代谢组（metabolome）层 面 以 及 生 物 体 层 面 的 表 型 特 征（phenome），成为科学家研究复杂疾病的宝贵资源。无疑，基因大数据将对现有医学研究、个体化医疗产生颠覆性的影响。

全基因组关联分析（genome-wide association studies，GWAS）在基因大数据的研究中处于基础性地位。以GWAS为基础的大量研究项目的开展，开启了人类对各种复杂疾病的遗传结构的探索。GWAS采用高通量的方式获取全基因组的上百万个遗传变异位点——单核苷酸变异（single-nucleotide polymorphsim， SNP），并对这些变异点和复杂疾病或性状进行关联分析，找出风险变异点。截至2019年4月，已经公开发表的GWAS研究达3 923个，发现了约134 705个与疾病或性状显著关联的变异位点（显著性检验的p值<5×10^-8）。大部分的研究结果可在全基因组关联分析数据库中获得。这些结果将基因组和生物体表型组联系起来，极大地增进了人们对生物体表型的遗传学结构的认识。随着GWAS研究越来越受到重视，大规模的研究也在不断推进。例如，英国生物样本库（UK Biobank）成立于2006年，迄今为止，UK Biobank收集了约50万人的DNA测序数据以及大量与疾病和健康相关的表征数据，包括生理指标、生活方式、血液和尿液采样、大脑和身体成像数据以及参与者的医疗记录、电子病历数据等。这种从基因测序数据、表征数据到医疗成像数据和电子病历数据的多维度积累为科学家进行复杂疾病的研究提供了数据支撑，将助力于个性化的精准医疗服务。

尽管GWAS的研究取得了令人瞩目的成绩，然而单独的GWAS研究往往只考虑基因组层面与表型特征的信息，忽略了生命过程中其他层面的相关信息，无法贯穿从遗传变异到表型特征的整条证据链。因此需要整合和集成从遗传变异到生命体表征的多组学层面的信息并进行分析，从而全方位解析从遗传变异到表型特征的整个因果链条。这里的多组学层面包括基因组层面、表观基因组层面、转录组层面、蛋白质组层面、代谢组层面以及生命体表征组层面的表型特征（如图1所示）。伴随着各项大型生物医疗国际项目的开展，这些多层面、多维度、高质量的基因大数据正在不断产生和积累。2012年9月完成的DNA元件百科全书项目（encyclopedia of DNA elements project，ENCODE项目）是继人类基因组计划后又一重要的突破性工程。该项目对大部分非编码序列（约占全基因组的98%）的功能进行了注释，例如“这部分序列与一种蛋白质结合”“这部分序列常被甲基基团标记”“这部分序列通常隐藏在组蛋白的包围中”。随之开展的表观基因组的图谱计划（roadmap epigenomics project）直接从人体的细胞系或组织中取样，并将其数据向公众开放。这些结果将为研究人类细胞系和组织的表观基因组功能发挥重要的作用。与此同时，2010年开始的基因型-组织表达（genotype-tissue expression， GTEX）项目于2013公开数据库，到目前为止收集了约714个捐献者53个人体组织的11 688个样本数据，用于研究不同组织中基因型与表达型的关系，完成了基因组到转录组的跨越，为科学家提供了宝贵的资源库。此外，现代核磁共振技术、质谱和色谱等技术的发展使得对大规模的生物体小分子的定量研究成为可能，这也大大促进了蛋白质组层面和代谢组层面研究的发展。目前已公布的蛋白质层面和代谢组层面的研究达80多项，产生了大量可公开获取的数据。

图1   多组学层面的数据

这些多层面、多维度、高质量的基因大数据为刻画完整的疾病产生的因果链条创造了条件，同时也促进了该领域集成分析方法研究的发展。本文总结了当前基因大数据的集成分析的一些研究进展，这些研究大部分基于多基因遗传结构（多个基因影响一个性状）的共识以及以下两方面的科学发现：遗传变异的多效性（一个变异影响多种表型）以及非编码遗传变异的调控功能。具体地，本文对基因大数据的集成分析从以下3个方面进行综述：检测风险位点及其功能分析；基因多效性的分析；基于孟德尔随机化的因果推断。本文进一步结合具体的应用案例进行分析，最后对基因大数据的集成分析研究进行了总结以及展望。

2 基因大数据集成分析的科学依据

2.1 多基因遗传结构

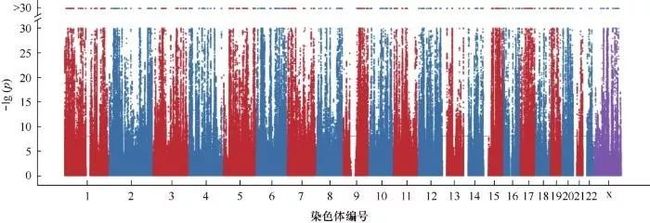
复杂性状或疾病的多基因遗传结构是指复杂性状和疾病的变异是由多个基因共同影响的。尽管科学家在GWAS研究中发现了很多显著的变异位点，但是这些显著的变异位点只能解释性状方差的小部分，这个现象通常被称为“丢失的遗传率（missing heritability）”。以人体身高这一性状为例，根据以往对家庭谱系的研究，已经存在的广泛认识是人类身高的遗传率达70%~80%等。多基因遗传结构的存在使得GWAS研究面临着诸多挑战：第一，多基因结构意味着单个基因对性状的贡献是微弱的，受GWAS样本量的限制，单个GWAS研究很难找到遗传变异中微弱的信号点；第二，常用的基于稀疏和强信号假设的建模方法在这里不再适用。图2中横轴为染色体编号，每个SNP按染色体上的位置排列，纵轴为对应SNP的GWAS统计检验的-lg(p)。图中顶部的点对应-lg(p)>30的SNP。

图2 身高的曼哈顿图

        基于多基因遗传结构的假设，线性混合模型（LMM）开始受到关注。以遗传率的估算为例，假设已经获取n个个体的M个SNP的标准化后的基因测序数据G∈R ^n×M，对应的表型（如身高）数据y∈R^n×1，X∈R^n×p表示 p个协变 量信息（如年龄、性别和一些用以控制群体分层的主成分数据），它们之间的关系可以由线性混合模型来建立，具体如下：

其中，β∈R^p×1是固定效应，u∈R^M×1是随机效应，e是由环境因素引起的随机误差。这里假设u和e都是正态分布的，即和。式（1）建立起了基因型与表型的关系。由遗传率的定义（基因型方差在表型方差中的占比）及以上线性混合模型，可以得到遗传率的计算式为：

限制极大似然估计（REML）和最大期望算法（expectation-maximization algorithm，EM）常被用于估算遗传率，如全基因组复杂性状分析（genome-wide complex trait analysis，GCTA）工具。

2.2 基因的多效性

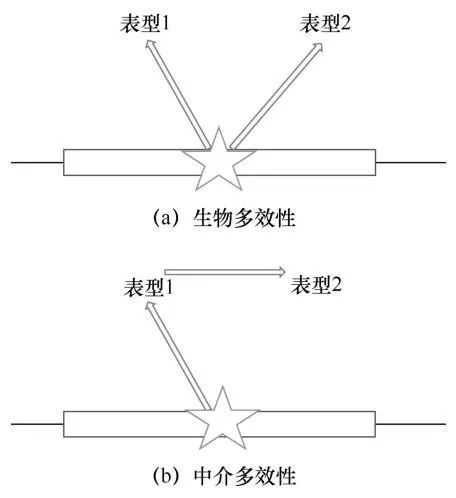
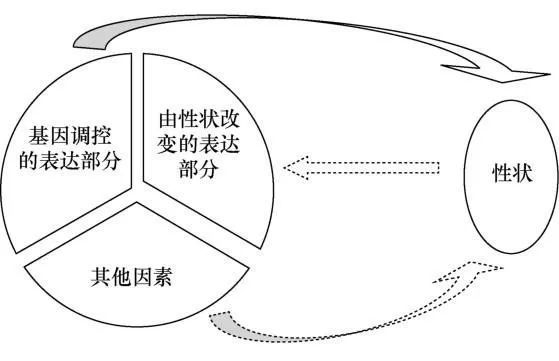
基因的多效性（pleiotropy）是指一个基因影响着多种表型。基因的多效性广泛存在于复杂性状中，具体的例子有：与维生素D缺乏症强相关的CYP2R1基因会同时导致多发性硬化症；CLPTM1基因同时影响神经胶质瘤、膀胱癌和肺癌；基因多效性大量存在于自身免疫综合征和精神疾病中。根据遗传变异影响性状的机制，基因多效性主要可分为两大类：一类是基因的生物多效性（biological pleiotropy），即基因直接影响多种表型；另一类是基因的中介多效性（mediated pleiotropy），即基因通过影响一种表型对另一种表型产生影响（如图3所示）。以肥胖基因（FTO基因）为例，研究者发现，该基因对骨关节炎的影响是通过影响体质指数（body mass index，BMI）来传递的。基因的中介多效性在探索复杂疾病或性状之间的因果关系中有重要的作用。

图3   基因多效性

基因多效性的存在引导人们集成多个GWAS数据一起研究。一方面，基因的多效性可以帮助人们探索复杂疾病之间的关系，如遗传相关性、基于孟德尔随机化的复杂疾病的因果推断等；另一方面，由于多基因遗传结构的存在，单独分析一个GWAS会导致具备微弱效应的遗传位点很难被检测到。集成多个与遗传相关的复杂性状的GWA S数据，通过建立有效的统计模型，可以帮助检测到更多的多效性位点，从而提高统计分析的效率。

2.3 基因的调控功能

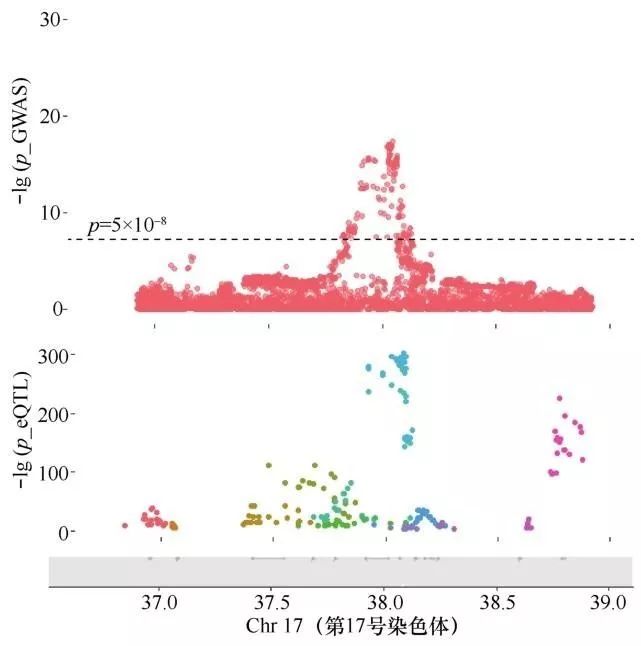
作为基本的遗传单位，基因是一段有功能性的DNA序列。基因中大部分位点（如启动子和增强子）处于非编码区，不参与基因编码，但对基因的转录、翻译和表达起着重要的调控作用。对于整体的DNA序列，只有少部分位于基因的调控区，参与基因编码，能够转录为信使RNA，进而指导蛋白质的合成。ENCODE项目对人类基因序列进行了详细分析，研究结果显示，在98%人类非编码区的序列中，81%保持着生物活性。大量证据显示，在GWAS发现的与众多复杂性状相关的位点中，大部分位点处在基因的非编码区。比如，科学家调查5 654个非编码区位点（这些位点与654种复杂疾病相关联），发现76.6%的位点处于脱氧核糖核酸酶I高敏区（DHS），这一区域与基因的转录功能高度相关。基于转录组层面的研究发现，大量与疾病关联的位点位于表达数量性状基因座（expression quantitative trait loci， eQTL）（如图4所示）以及转录因子结合位点（transcription factor binding sites，TF）。在最新的一项关于精神分裂症（schizophrenia，SCZ）的研究中发现，在与SCZ相关的100多个基因位点中，有超过20%的位点与基因的表达和调控机制相关。这些研究结果表明，与疾病关联的风险变异点可能不直接参与基因编码，而是通过调控基因的转录、表达或翻译中的任何一个环节发挥作用。因此将疾病的GWAS数据和功能型数据集成并进行分析，能够深化人们对疾病的遗传机理的认识。

图4   与疾病关联的位点常富集于表达数量性状基因座

3 基因大数据的集成分析方法

基于上述科学进展，本节将从以下3个方面对基因大数据的集成分析进行综述。

● 检测风险位点及其功能分析：该类型方法集成GWAS数据和多组学数据（如变异位点功能型数据、转录组的基因表达数据等），力图找到更多的危险变异点，并对变异点的生理功能进行分析。

● 基因多效性的分析：该类方法集成多个GWAS数据以及多组学数据，从而探索复杂疾病遗传上的相关关系以及共同的致病基因。

● 基于孟德尔随机化的因果推断：该类型方法集成多种风险因素和疾病的GWAS数据，探讨风险因素（如血压、体重、代谢物等）对疾病的影响。

为描述方便，先对使用的数据类型进行介绍。在基因大数据的集成分析中使用的数据主要包括两种类型：第一类是个体样本层面的数据，该类型数据包含每个样本的基因型、每个样本的疾病状态（糖尿病、高血压或者健康）等；第二类是概括型数据，该类型数据是指对于个体样本层面的数据通过关联分析得到每一个SNP与疾病的概括性统计量，包括回归效应的估计值、标准差、检验统计量、p值等。因为使用的数据类型不同，集成分析方法也会存在差异。

3.1 风险遗传变异的检测及功能

由于与疾病相关的位点总是具备某些调控功能，将相关位点的调控功能信息植入某种疾病的GWAS数据分析中，能帮助人们找到真正的风险遗传变异点，深入地研究遗传变异的功能。在这个研究领域里，贝叶斯方法被大量运用到GWAS数据与调控信息数据的集成分析中。该类方法对疾病的GWAS个体层面数据或概括性数据（用G表示）进行分析，同时引入功能型数据或基因表达数据（用A表示），推断遗传变异位点L（可以是一个基因也可以是单个SNP）是否为疾病发生的风险位点（见计算式（3））。基于模型分析的结果可以进一步对变异点进行功能分析。在这里，笔者介绍两类风险遗传变异检测的集成分析方法：第一类是结合功能型数据的集成分析；第二类是结合基因表达数据的集成分析。

P(L是危险变异点│G WA S数据G，功能型数据A) （3）

3.1.1 结合功能型数据的集成分析

假设已经收集了M个位点的D列功能型数据，并存放在矩阵A中，A中对应的第i行、第j列的元素记为A_{i j}，代表第i个SNP的第j种功能型的取值。以eQTL数据为例，假设A中的每一列对应人体的不同组织器官（如心脏、大脑、肝脏等）。如果第i个SNP能够调节第j个组织中某个基因的表达，那么这个SNP是第j个组织的一个eQTL，则A_{i j}取1，否则取0。将需要分析的SNP与已有的功能型数据库进行匹配，就可以产生矩阵A。下面以一种常用的统计模型为例来阐述GWAS数据与功能型数据的集成分析。

假设观测到n个个体样本的表型数据（记为y∈R_n）及对应的基因型数据（用矩阵X^n×Mn×M表示），那么，对于第i个样本个体，其表型数据yi与其基因型数据X_i1,⋯,X_iM可以建立以下线性关系：

其中，β₁⋯β_M 为回归系数，εi 为残差项，且服从正态分布N(0,σ2)。若回归系数β_j不为0，则代表第i个变异位点与疾病相关，因此进一步假设存在一个指示变量γ_j ，γ_j可取0和1，分别代表β_j等于0和β_j不等于0。具体来说，β_j与γ_j的关系可以通过以下模型建立：

接下来通过一个Logistic模型建立γ_j与第i个SNP的功能型数据信息A_j（即矩阵A中的第j行）的关系：

其中，θ∈R^K和θ₀是需要估计的参数。若θ中的某个元素不为0，代表疾病的致病基因可能与对应的功能组相关。也就是说，如果知道某个SNP的功能信息，引入这些信息能够调整γ_j的先验分布，模型会自动给与疾病相关性高的某种功能型的位点赋予更高的权重，从而提高统计分析的效率。若模型的参数估计结果已经得到，通过计算在给定y、G、A下γ_j取1或0的后验概率，可以推断γ_j取1或0的概率，从而可以检测该变异位点是否属于风险变异点。对模型的参数进行统计推断可以对该变异位点进行功能分析。

上述模型的框架可以扩展到GWAS概括性数据建模分析中，如可以对概括性统计量的假设检验的p值进行建模，通过假设p值来自一个由均匀分布和Beta分布组成的混合分布，建立起p值（如p_i）与指示变量γ_i的联系。具体来说，假设观测得到的p值用p_i,⋯,p_n表示，即与疾病不相关的SNP来自[0,1]区间的均匀分布U（0,1），对应的指示变量γ_j此时取1，而与疾病相关的SNP的p值来自Beta分布Betta(a,1)，对应的指示变量取0，具体如下：

类似地，可以通过Logistic模型（见计算式（6））建立起γ_j与第j个SNP的功能型数据信息A_j的联系。最大期望算法常用于求解上述模型的参数，目前的研究已经可以满足集成大规模功能型数据的分析和计算的需求。

近年来，深度学习作为一种机器学习技术开始得到越来越多的关注，在图像识别和自然语言处理等领域取得了突破性进展。因其优异的数据处理能力，深度学习也开始被逐步应用于探索人类基因组密码，尤其是功能基因（functional genomics）组学。例如，2015年提出的DeepSEA，该方法将公开的多组学功能型数据（ENCODE功能型数据，表观基因组的图谱计划）作为输入，搭建深度学习模型，从而实现对非编码区域遗传变异位点（占人体基因组的98%）的功能分析。2016年提出的DeepWAS首先基于DeepSEA找到潜在的影响疾病的某一类型的功能型位点，然后再构造带惩罚函数的多元回归模型（LASSO），实现风险变异位点的检测。单独的GWAS分析只能确定某个变异点与疾病的关联性，DeepWAS则能够更加综合地分析致病基因突变，帮助寻找其致病机理。实际应用显示，集成分析GWAS数据和功能型数据不仅可以帮助检测新的危险变异，而且对探索疾病的发病机制有非常重要的作用。

3.1.2 结合基因表达数据的集成分析

结合基因表达数据的集成分析方法有PrediXcan、MetaXcan、TWAS以及CoMM。该类型方法的基本思想是以已有的基因表达样本库的数据为参考面，估算GWA S的个体的基因表达，然后检测基因表达和表征是否关联，其基本原理如图5所示，此类方法的目的在于对基因调控的表达部分和性状进行关联分析（图5中实线箭头）。以CoMM为例。假设参考面的某个基因的基因表达数据以及基因型数据为y_1g和X_1g，感兴趣的疾病或性状的表型和基因型数据为y₂和X _2g，这里基因的表达数据和GWAS个体层面的数据是不同的样本，基因表达型数据和GWAS数据的关系通过共享参数u来建立，具体如下：

图5   基因表达的数据和疾病的GWAS数据的集成分析基本原理

其中，α_g为未知参数，通过检验α_g是否为0，可以推断基因表示与表征的关系。基于多基因效应的假设，这里假设u服从以0为均值，以为方差的多元正态分布，即u∼N(0,) 。e₁、e₂为误差项且服从零均值正态分布。该方法将基因表达数据和疾病或性状的GWAS数据进行联合建模和估计，考虑了估算基因表达的不确定性，显示出更高的统计效率。这类型方法也可以推广到其他层面的组学数据（如蛋白组层面）和GWAS的集成分析研究中，具有极高的应用价值。

3.2 遗传变异的多效性

遗传变异的多效性的存在决定人们可以集成多个GWAS数据进行分析。一方面，可以探讨复杂疾病在遗传结构上的相关关系，这种相关关系在某种程度上可以反映复杂疾病之间的联系；另一方面，利用这种多效性设计有效的统计模型，可以帮助人们找到更多与多种复杂疾病相关的多效性位点，同时，通过引入功能型数据进行分析，能进一步提高人们对疾病的遗传机理的认识。

复杂疾病在遗传结构上的相关关系可以通过遗传相关系数这一参数来度量，该参数反映两个复杂性状中由遗传效应引起的总体相关性程度。常见疾病（如心脏病、糖尿病、脂类代谢异常以及高血压）两两之间存在较强的遗传相关系数（0.27~0.43），反映了遗传变异在这一类型的疾病中具有比较一致的效应。基于线性混合模型，可以先了解遗传相关系数的定义。假设已经获取两个独立样本的关于两个表征的观测数据以及个体层面的基因测序数据（标准化后），表示为：y₁∈R^n1×1， G₁∈R^n1×m，y₂∈R^n2×1，G₂∈R^n2×1，对应的协变量信息用X₁∈R^n1×p1、X₂∈R^n2×p2表示，这里的下标对应两个不同表征型，它们之间的关系由以下线性混合模型来建立：

基于多基因效应，假设：

其中，分别为u₁和u₂的方差，ρ为u₁和u₂的相关系数，即遗传相关系数，其取值范围为[-1,1]。极大似然估计或限制性极大似然估计等方法常用于二元混合模型的参数估计。此外，基于概括性数据的LDScore回归方法，可以针对任意两个性状进行分析，并且能有效地处理样本重合的影响。在该方法的基础上，研究者们提出了GNOVA，该方法可以计算不同性状在功能型位点的分区遗传相关程度，能够帮助人们更具体地了解疾病的遗传特征。

更重要的是，集成多个GWAS数据的分析方法可以帮助人们进行多效性位点的检测。研究者们通过对比不同性状或疾病的GWAS研究的显著位点，可以标注多效性基因位点。然而这种方法只考虑了显著位点，因而缺乏统计效率。通过集成分析多个不同性状的全基因组的GWAS数据（不只考虑显著位点），建立有效的统计模型，可以检测更多的风险变异点，并发现更多的多效性位点，进而提高统计分析的效率。多变量的线性混合模型也常被用于关联变异位点的检测，显示出比一元线性混合模型更大的统计效率。目前常用的工具有GEMMA、mvLMM和BOLTREML等。该类型方法在实际应用中往往受到很多限制，原因在于这类型方法需要用到GWAS个体层面的数据。受数据可获得性和数据隐私保护等的限制，获取GWAS个体层面的数据往往会比较困难。基于概括性数据的多个GWAS的集成分析，只需要GWAS概括性数据，而且不同性状的GWAS数据可以来自不同的生物样本集（考虑到基因的种群效应，一般要求GWAS数据来自同种群），有利于大规模的集成分析。同时，该类型方法能够更灵活地引入功能型数据，提高模型的统计效率。基于隐变量的统计模型在GWAS的集成分析中扮演着重要的角色。以基于基因多效性和功能型数据的遗传分析（genetic analysis incorporating pleiotropy and annotation,GPA）方法为例，该方法基于概括性统计量（p值），集成分析多个GWA S数据和功能型数据，能有效地检测出多效性位点。假设收集到K个GWAS的M个SNP的p值，存放在一个M×K维的矩阵中，用P表示，其中p_jk代表第j个SNP在第k个GWAS的p值。类似于单个GWAS危险变异的检测，这里也假设存在一个M×K维的隐变量矩阵Z，Z_jk取0代表第j个SNP和第k个GWAS无关，Z_jk取1代表第j个SNP和第k个GWAS有关。变量之间对应的关系可以通过下列模型表示：

以k=2为例，定义：

这里π₀₀、π₀₁、π₁₀、π₁₁分别表示Z _j1、Z_j2取不同值的比例，并且π₀₀+π₀₁+π₁₀+π₁₁=1，进一步地，GPA假设在给定GWAS的关联状态下，SNP的功能性状态之间独立。

在GPA模型中，π₀₀,π₀₁,π₁₀,π₁₁,q_00k,q_01k,q_10k,q_11k以及a₁,a₂为模型的未知参数，EM类型的算法可以有效地解决该模型的参数估计问题。模型通过计算局部错误发现率（false positive rate， FDR）Pr(Z_j1,Z_j2|P,A)、Pr(Z_j1|P,A)和和P和Pr(Z_j2|P,A)来检测多效性位点以及单个GWAS的风险变异点；对 q_00k,q_01k,q_10k,q_11k,进行显著性检验可以检测与疾病相关联的位点在第k类功能型上的富集情况。

进一步的研究显示，通过Logistic回归和Probit回归实现隐变量和功能型数据的建模，可以解决GPA模型只能引入离散型、功能型数据的局限。同时，在多个GWAS数据的集成分析中，低秩性和稀疏性的叠加模型以及复合极大似然方法的使用，完美地避免了模型参数指数增长而无法估计的问题。

3.3 基于孟德尔随机化法的复杂性状因果推断

基因的多效性普遍存在于人类基因组中，对复杂疾病的研究具有重要的价值。基因的中介多效性可以用来探索复杂疾病或性状之间的因果关系，这类型的方法被称作孟德尔随机化法（Mendelian randomization，MR）。该方法可追溯至1986年，Katan M B提出载脂蛋白E （APOE）基因的变异（包括E2/E3/E4）能够影响体内胆固醇的水平，其中携带E2基因的人血浆胆固醇水平较低。由于亲代到子代等位基因的随机分配，个体APOE基因的携带情况不受其他混杂因素的影响。因此，可通过癌症病人和非癌症病人的E2基因携带情况是否存在差异来判断低水平血浆胆固醇是否会增加癌症风险。孟德尔随机化法这一术语在1991年第一次被提出，逐渐成为因果推断中的主流方法。该方法以基因变异（如APOE）为工具变量来研究暴露因素（如血浆胆固醇水平）和结局变量（如癌症）之间的因果关系，可以突破传统的观察性流行病学在研究因果关系方面的多种限制，如反向因果、混杂因素等。近几年来，基于GWAS概括性数据的MR分析方法的发展更能体现出其方法上的优越性。首先，大量GWAS概括性数据的可公开获得为研究者们提供了丰富的数据资源。MR检验可以在任意的性状之间进行，大大扩展了因果关系的可研究范围。相比之下，传统的随机控制实验往往受到实验伦理以及试验设计的局限，对于罕见疾病的研究，往往因数据收集方面的困难而无法进行；其次，GWAS的研究基本上是基于大样本的研究，目前还在不断朝着更大样本规模发展，MR因果分析也将受益于次。

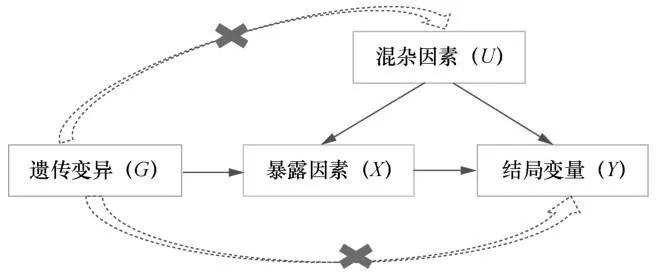
孟德尔随机化法以遗传变异（G）为工具变量，在推断暴露因素（X）对结局变量（Y）的因果关系时，需要满足以下3条基本条件：①G和X相关；②假设存在混杂因素（U）同时影响暴露因素和结局变量，G和U无关；③G只能通过X影响Y，而不能存在其他的通道影响Y。只有在这3个条件同时满足的情况下，MR方法才能正确地推断X和Y的因果关系 （如图6所示）。具体来说，条件①要求在做MR分析时，必须选择与X显著相关的位点，比如p<5×10-8。根据孟德尔遗传定律，总是假设条件②成立，然而其他因素（如群体分层、样本的重合）可能会导致这个条件不符合，因此在实际应用中选择的GWAS数据需来自同一种群且应避免存在样本重合；条件③要求G对Y不能有直接的影响，G对X和Y只能存在中介多效性。基因中介多效性也常被称作垂直多效性，对应的基因的生物多效性也称作水平多效性，用以描述基因与性状之间的直接联系。水平多效性的存在会影响MR分析结果的可靠性。

图6   孟德尔随机化法基本原理

MR分析中各变量间（包括G、X、Y、U）的关系可通过下面的线性结构方程来描述：

其中，为M个独立的变异位点，γ_j为G _j对X的效应大小（effect size），α_j为G_j对Y的效应大小。若该变异位点满足MR分析的假设，则α_j=0；若存在水平多效性，则α_j≠0。η_x和η_j表示混杂因素对X和Y的影响大小，E_x和E_y为对应的残差向量，β表示X对Y的影响效应的大小，若β不为0，则表示X和Y存在因果关系。MR分析的目的是准确地估计β的大小并进行因果关系的检验。上述模型要求GWAS个体层面的数据，而基于两样本的GWAS概括性统计量的MR分析方法不受数据的隐私保护等限制，逐渐成为热点。这时，观测到的数据为变异位点对暴露因素（X）和结局变量（Y）的回归效应（effect）的估计值及其标准差，记为，它们的关系可以表示为：

由于两组数据来自无样本重合的GWAS研究，γˆj与 Γˆj相互独立（给定的情况下）。若变异位点均满足MR假设条件，不存在水平多效性，则α_j =0，j=1,⋯n；若存在某几个α_j不为0，由于会影响β的估计，则会被当作异常点。若所有位点均存在水平多效性但平均水平为0，则称为平衡的水平多效性或系统性多效性，反之则称为非平衡的水平多效性或有向多效性。

目前关于MR的大量研究集中在处理变异位点的水平多效性方面，研究方法可大致分为3种类型。一类是矫正，如MREgger通过在传统的异方差加权模型（inverse variance weighted，IVW）中引入常数项，修正由于非平衡的水平多效性（αj的均值不为0）对模型带来的影响。该方法往往会引入较大的估计方差，降低统计效率。第二类是异常值剔除，这类型方法（如MR-PRESSO、GSMR等）先对可能存在水平效应的异常位点进行检测，剔除检测到的异常位点，然后对模型参数重新估计。这类方法在存在少量的异常点时是有效的，但当存在大量的异常点或平衡的水平效应时，则需谨慎使用。第三类方法是对违背MR假设的变异点进行具体的建模，如MR.raps和BWMR等。MR.raps和BWMR均假设存在系统性的水平效应，而且αj服从零均值的正态分布，MR.raps在使用似然方法进行参数估计时，用稳健的损失函数Tukey损失函数和Huber损失函数取缔了均方损失函数，以得到稳健的估计。BWMR则引入贝叶斯重加权（Bayesian reweighting）的思想，通过赋予异常点较低的权重来降低异常点的影响。

基于概括型统计量的MR分析，集成来自不同样本的GWAS研究数据，可以推断出不同性状之间的因果关系，对了解复杂疾病的发病机制、疾病的干预治疗以及制药等方面具有重要的推进作用。

4 应用案例

4.1 基因多效性分析：运用于神经质和重度抑郁症GWAS数据分析

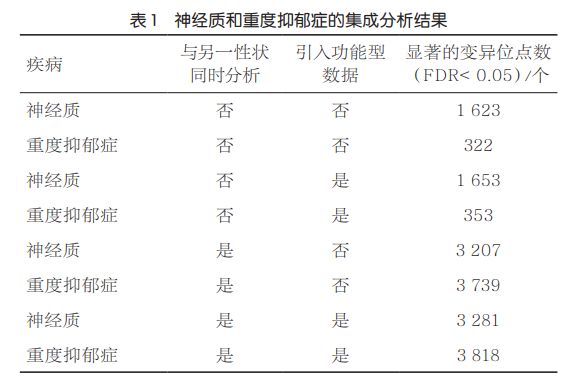
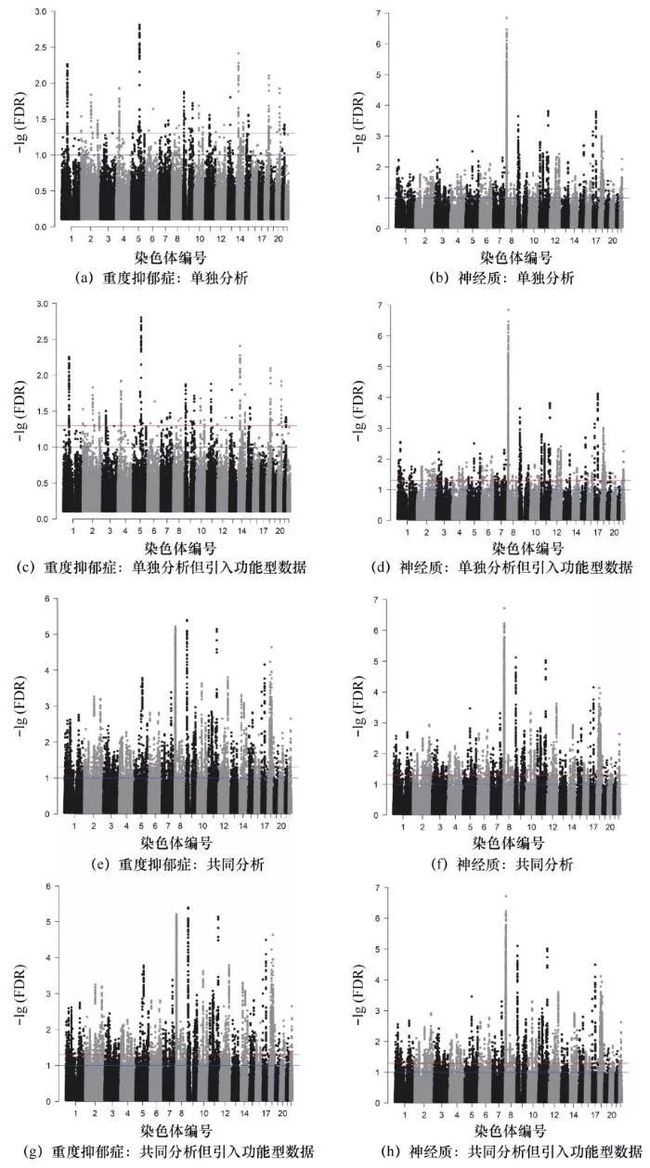
心理学上描述人的五大性格特质包括：开放性、责任性、外倾性、宜人性和神经质，其中神经质主要反映平衡焦虑、敌对、压抑、自我意识、冲动、脆弱等情绪的能力，即维持情绪稳定性的能力。已有的研究表明，神经质和重度抑郁症（major depression disorder，MDD）存在较强的关联，在遗传上存在较强的相关性。本文基于GPA方法对已有的神经质和重度抑郁症的GWAS概括型数据和功能型数据（这里使用eQTL数据）进行基因的多效性分析，以探索这两种性状在遗传上的关系。集成分析结果见表1，曼哈顿图如图7所示。集成两组GWAS数据进行分析显示出更高的统计效率，原因在于这两组疾病具有高度相似的遗传学机理。根据参数估计结果，πˆ00=0.793，πˆ01=0.014，πˆ10=0，πˆ11=0.194，其中，πˆ11=0.194（似然比检验p=0）表明神经质和重度抑郁症具有高度相似的遗传机理，也就是说两个性状共享信息，共同分析两个GWAS数据能极大地提高效率。此外，表1的结果显示通过集成功能型数据，能发现更多的显著位点，进一步提高统计效率。

图7   神经质和重度抑郁症的 曼哈顿图（蓝线和红线分别对应局部错误率为0.1和0.05）

4.2 血脂代谢物与人类复杂疾病的因果关系

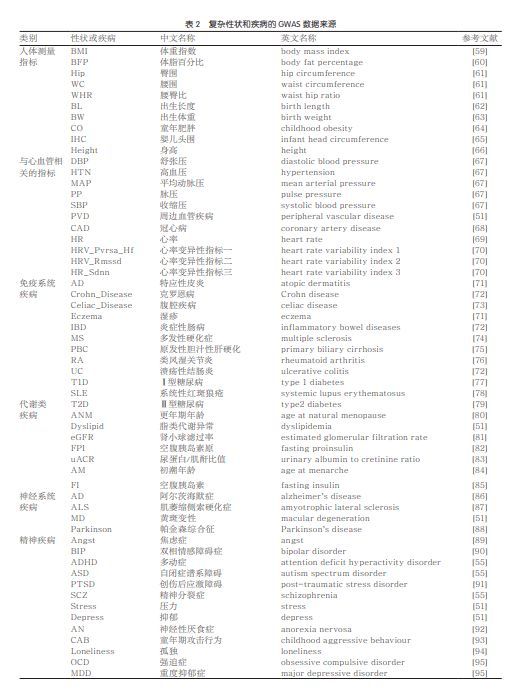
本节基于101种分子水平的血脂代谢物和57种人类复杂疾病的GWAS概括型数据，探讨集成分析在实际中的应用。复杂性状或疾病的GWAS数据来源见表2，血脂代谢物包含87种血脂蛋白携带的脂类物质以及14种游离的脂肪酸或相关度量。脂类物质包括总胆固醇（total cholesterol，C）、胆固醇酯（cholesterol esters，CE）、总脂质（total lipids， L）、磷脂（phospholipids，P）、游离胆固醇（free cholesterol，FC）、甘油三酯（triglycerides，TG）。血脂蛋白根据密度可分为低密度脂蛋白（low-density lipoprotein，LDL）、高密度脂蛋白（highdensity lipoprotein，HDL）、极低密度脂蛋白（very-low lipoprotein，VLDL）、中密度脂蛋白（intermediate-density lipoprotein，IDL）。各类血脂蛋白根据大小可以进行细分，如LDL可分为L.LDL、M.LDL、S.LDL等。57种人类复杂疾病包括与人体测量相关的性状（如身高、体脂指数（BMI）等）、与心血管相关性状（如冠心病（CAD）、收缩压（SBP）、舒张压（DBP）等）、代谢类疾病（如Ⅱ型糖尿病、脂类代谢异常等）、中枢神经系统疾病（如阿尔茨海默症、帕金森综合征等）、精神疾病（如重度抑郁症、多动症等）以及自身免疫疾病（如Ⅰ型糖尿病、系统性红斑狼疮等）。具体的分析分两方面：一方面，基于基因的多效性系统地探讨血脂代谢物和复杂疾病在遗传上的相关关系，对了解复杂疾病的遗传结构和性质具有重要的作用，本文基于GNOVA方法，对血脂代谢物和与人类复杂疾病的遗传相关系数进行估计；另一方面，血脂代谢物和复杂疾病的因果关系一直是科学家们关注的重点，对于疾病的预防和诊断具有重要的指导作用。以心血管疾病为例，目前大量的研究表明，血液中的低密度胆固醇是造成心血管疾病的主要原因。本文应用BWMR方法，对血脂代谢物和人类复杂疾病的因果关系和反向因果关系进行分析，从而深化对血脂代谢物和复杂疾病的认识。

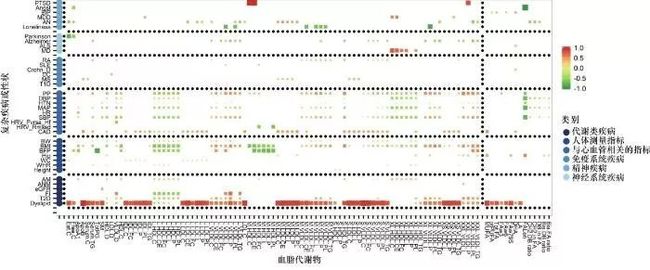
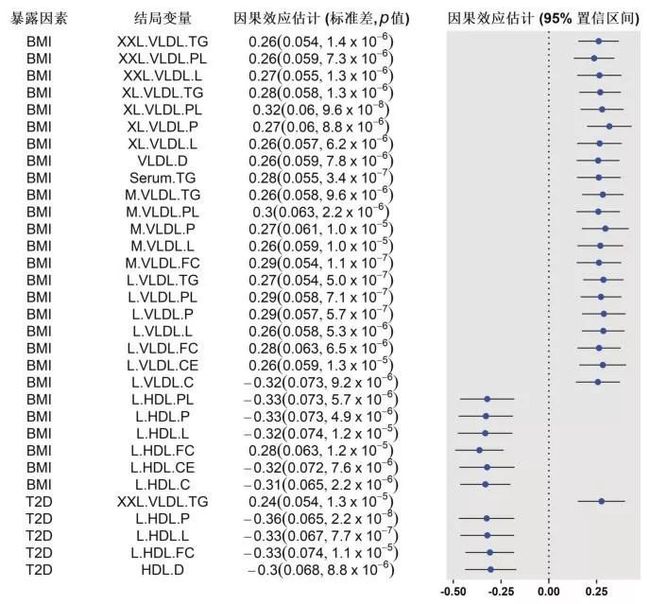
图8展示的是通过Bonferroni校正之后显著的遗传相关系数（p<0.05/(101×57)），其中640对具备显著的遗传相关关系。图8中红色为正相关，绿色为负相关，颜色深度和方格面积表示相关系数的大小，颜色越深或方格面积越大表示遗传相关系数越大。遗传相关系数的估计需调用GNOVA方法的软件包。结果显示，大部分复杂疾病与大部分血脂代谢物水平均有显著的遗传上的相关关系，如心血管疾病、高血压疾病、血压相关度量、体重相关度量等。此外，阿尔茨海默症、神经性厌食症与多种类型的血脂代谢物有密切的关系。值得注意的是，双相情感障碍症与多种游离脂肪酸有显著的遗传上的相关关系。因果分析结果显示，体质指数、Ⅱ型糖尿病会影响体内血脂代谢物的水平（结果如图9所示）。

图8   血脂代谢物（101种）与复杂疾病或性状（57种）的相关系数

图9   血脂代谢物和复杂性状的因果分析结果

5 结束语

本文对GWA S研究中的集成分析进行了综述，主要应用于以下3个方面：检测风险位点及其功能分析、基因多效性的分析、基于孟德尔随机化的因果推断。实际应用显示，集成分析在GWAS研究中显示出重要的作用，有助于挖掘重要的信息。同时，多种类型的集成分析统计方法具备极大的拓展空间，将对未来的研究发挥更大的价值。未来GWAS的集成分析将更多地应用于集成多组学数据的分析，对探索从遗传变异到疾病发生的整个因果链条起着重要作用。随着越来越多的高质量数据的不断产生，全方位生物医疗大数据（包括基因大数据、医疗图像数据、电子病历等）的集成分析将使得实现个性化的精准医疗成为可能。

作者简介

胡湘红（1991- ），女，深圳市大数据研究院博士生，主要研究方向为生物信息。

彭衡（1974- ），男，香港浸会大学数学系副教授，主要研究方向为金融计量经济学、生物信息、模型选 择、非参数方法。

杨灿（1980- ），男，香港科技大学数学系助理教授，主要研究方向为生物信息学、高维数据分析、统计遗传学。

张纵辉（1981- ），男，深圳市大数据研究院副教授，主要研究方向为信号处理、最优化方法、数据通信。

万翔（1972- ），男，深圳市大数据研究院研究科学家，主要研究方向为机器学习、医疗大数据、生物信息。

罗智泉（1963- ），男，深圳市大数据研究院教授，主要研究方向为最优化方法、算法设计、信息科学。

《大数据》期刊

《大数据（Big Data Research，BDR）》双月刊是由中华人民共和国工业和信息化部主管，人民邮电出版社主办，中国计算机学会大数据专家委员会学术指导，北京信通传媒有限责任公司出版的中文科技核心期刊。

关注《大数据》期刊微信公众号，获取更多内容

---

往期文章回顾

面向大数据的索引结构研究进展

基于图查询系统的图计算引擎

大数据环境下的存储系统构建：挑战、方法和趋势

一种软硬件结合的大数据访存踪迹收集分析工具集

开源芯片、RISC-V与敏捷开发

---