二叉搜索树 详解,中序遍历伪代码 ,AVL原理讲解【c++详解】(含代码)
本篇文章持续更新
文章目录
- 一般二叉搜索树
-
- 一、概述,循关键码访问
- 二、单调性和有序性,查找操作
-
- hot
- 三、插入和删除
-
-
- 1,无后代
- 2、单分支
- 3、双分支
- 利用二叉查找树排序
-
-
- 递归实现
- 非递归实现
-
-
- 四、复杂度——退一步海阔天空
- 二叉搜索树代表——1.AVL树
https://blog.csdn.net/BZ_C25LX/article/details/127660068?spm=1001.2014.3001.5501
这篇文章中有更详细的解答,欢迎阅读!!
一般二叉搜索树
一、概述,循关键码访问
二叉搜索树是一种树形结构,可以说是vector和list的结合版,简称BST,平衡二叉搜索树是其中的一种,简称BBST。与其他数据结构一样,二叉搜索树也是有一组数据项所构成的集合,但与其他数据结构不同,二叉搜索树的访问方式采用的是循关键码访问(call-by-key)其中每一个数据项都拥有一个关键码key,每一个key也有与其对应的value.每一个数据项都有其唯一代表的值,称为关键码,通过关键码访问数据的方式我们称作循关键码访问。关键码支持比较和比对,数据集合中的每一个数据项都可以统一的表示和实现为词条(key,value)的形式,,词条也可以进行比较和比对,如果此树不能,那么就要进行操作符重载。这样一来,每一个数据项就有了其对应的三个要素:key-词条-关键码。
二、单调性和有序性,查找操作
另外,二叉搜索树为了方便搜索,其整棵树具有有序性和单调性,也就是说,每一个节点都不大于他的右后代,不小于他的左后代(不能是孩子),正是因为有了这样的规律,才使得每一颗二叉树的中序遍历具有单调递增性,我们可以发现,此时他已经变为了一个数组,这也是为什么我们刚才说BST是vector和list的结合,
二叉搜索树是用来查找,插入,和删除的,查找时秩只需比较查找的关键码和当前节点关键码即可。当需查找的关键码不小于当前关键码,则前往他的右孩子,反之亦然。当查找成功(关键码成功匹配时)或查找失败(其到达叶节点时查找结束)。
hot
不得不提的是,二叉搜索树中有一个常见的接口,其在插入操作,删除操作或其他的操作中经常用到,就是高度指向,也叫深度指向,其意思顾名思义就是指向当前深度的变量,一般写作_hot,hot是引用值类型当查找成功时,将返回想要查找的点的父节点,为了使语义统一,失败时将构造一个当前节点,再返回其父节点,也就是当前路径上最后一个真实存在的结点…。
三、插入和删除
插入操作较为简单,只需要依照查找的步骤找到需要插入的位置,随即进行插入就好了。
代码如下:
template <typename T> BinNodePosi<T> BST<T>::insert ( const T& e ) { //将关键码e插入BST树中
BinNodePosi<T> & x = search ( e ); if ( x ) return x; //确认目标不存在(留意对_hot的设置)
x = new BinNode<T> ( e, _hot ); //创建新节点x:以e为关键码,以_hot为父()
_size++; //更新全树规模
updateHeightAbove ( x ); //更新x及其历代祖先的高度
return x; //新插入的节点,必为叶子
} //无论e是否存在于原树中,返回时总有x->data == e
template <typename T> BinNodePosi<T> & BST<T>::search ( const T & e ) { //在BST中查找关键码e
if ( !_root || e == _root->data ) { _hot = NULL; return _root; } //空树,或恰在树根命中
for ( _hot = _root; ; ) { //否则,自顶而下
BinNodePosi<T> & v = ( e < _hot->data ) ? _hot->lc : _hot->rc; //确定方向,深入一层
if ( !v || e == v->data ) return v; _hot = v; //一旦命中或抵达叶子,随即返回
} //返回目标节点位置的引用,以便后续插入、删除操作
} //无论命中或失败,_hot均指向v之父亲(v是根时,hot为NULL)
而删除操作就较为复杂了,其关键在于如何在删除以后继续保持树内部的有序性和单调性。
一般分为三种情况:
1,无后代
需要删除的结点是叶节点,没有孩子,其直接删除即可,不用维护。
2、单分支
需要删除的结点只有左后代或只有右后代,操作也比较简单。删除此节点后只需将他的父节点和他的子节点直接连接即可。

3、双分支
就是需要删除的结点既有左孩子也有右孩子。我们可以通过一个很巧妙的方法将其删除,既然删除单分支结点如此简单,那么我们可以把问题化繁为简,也就是说,把双分支化为单分支,那么如何确定哪个结点一定是单分支呢,我们通过前面讲的二叉搜索树的中序遍历有序性可以不难得出,此节点的最近后继和前继一定是单分支结点,这样我们可以让需要删除的结点和其任意一个交换,再利用单分支结构的删除方法,将其删除即可,下面给出图示:
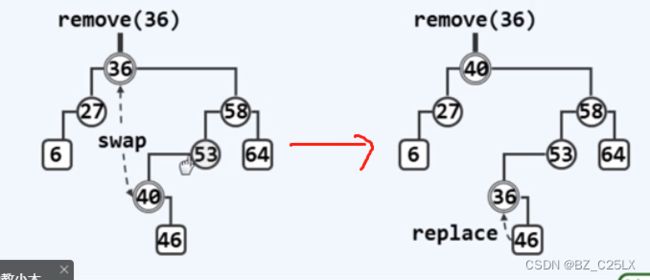
至于交换后树为何还能保持一颗BST,利用其中序遍历的单调性不难证明。
代码如下:
public boolean remove(int key) {
if(this.root == null) {
return false;
}
Node parent = null;
Node cur = this.root;
while (cur != null) {
if(cur.val == key) {
removeKey(parent,cur);
return true;
}
else if(cur.val < key) {
parent = cur;
cur = cur.right;
}
else{
parent = cur;
cur = cur.left;
}
}
return false;
}
public void removeKey(Node parent,Node cur) {
if(cur.left == null) {
if(cur == this.root) {//无分支
this.root = this.root.right;
}else if(cur == parent.left) {
parent.left = cur.right;
}else{
parent.right = cur.right;
}
}else if(cur.right == null) {//单分支
if(this.root == cur) {
this.root = this.root.left;
}
else if(cur == parent.left) {
parent.left = cur.left;
}
else{
parent.right = cur.left;
}
}else{//双分支
Node targetParent = cur;
Node target = cur.right;
while (target.left != null) {
targetParent = target;
target = target.left;
}
cur.val = target.val;
if(targetParent.left == target) {
targetParent.left = target.right;
}
else{
targetParent.right = target.right;
}
}
}
利用二叉查找树排序
我们可以利用搜索树的性质对一串数进行排序。首先,先将这一串树依次插入进二叉树中,其时间复杂度为,然后再得出二叉树的中序遍历序列,就得到了一串有序的数列,这个方法容易理解,其时间复杂度为O((n+2n+n*n)/2),相对来说没有十大排序算法那么快,但理解容易实现简单,下面给出中序遍历二叉树的伪代码:
递归实现
void midorder_traverse(const struct bi_tree *tree){
if (tree–>left) {
midorder_traverse(tree–>left);
}
access(tree–>data);
if (tree–>right) {
midorder_traverse(tree–>right);
}
}
非递归实现
void midorder_traverse(const struct bi_tree *tree){
struct stack s;
init_stack(&s);
const struct node *n = tree;
while (n) {
while (n–>left) {
s.push(n);
n = n->left;
}
access(n–>data);
while (n = s.pop()) {
access(n->data)
if (n–>right)
break;
}
}
四、复杂度——退一步海阔天空
二叉树虽然是一个很方便的树形结构,但却不够紧凑,其很难维护成比较方便的平衡二叉查找树,而如果树的形态维护的不够好的话,就会使其效率大打折扣。比如最坏情况下,树就会变成标准的一位链表,这时不论查找插入删除都打不到我们希望的O(logn).这个时候,我们需要对树的形态进行维护,如果变成一颗BBST,如图:

那么维护成本太高,也很难继续保持,这种形态是可遇不可求的,此时我们引进了一种新的概念,叫适度平衡也叫渐进平衡,其维护成本不高,平均复杂度也能渐进达到我们所期望的的效果,
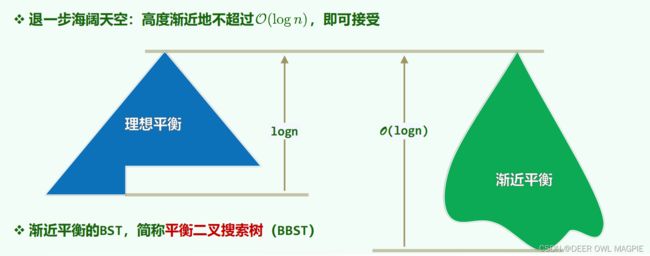
但与BBST还是无法相比,其适度平衡树,是指树保持一定的平衡,其维护成本很低的树的形态,代表有AVL树,红黑树等…。
二叉搜索树代表——1.AVL树
刚刚说了,为了保持二叉树的相对平衡,又不想花费太多的时间和空间去维护这种平衡,所以我们引进了一种概念,叫做渐进平衡,清华大学诗意的称作:退一步海阔天空。其中AVL树就是其典型代表,与一般二叉树不同的是,AVL树为了维持相对平衡,给每个结点增加了一个平衡因子,其规定,每个平衡因子值为左孩子的平衡值减去右孩子的平衡值,若某一个孩子为空,则他的平衡值为-1,这样就保持了相对平衡,其他操作与二叉搜索树一样,下图是,平衡因子的计算过程