机器学习-白板推导系列(十四)-隐马尔科夫(HMM，Hidden Markov Model)

14. 隐马尔科夫(HMM，Hidden Markov Model)

14.1 背景

14.1.1 概念回顾

1. 机器学习派别
   机器学习大致可分两派别：频率派和贝叶斯派的方法。
   • 频率派
     频率派的思想就衍生出了统计学习方法，统计学习方法的重点在于优化，找loss function。频率派的方法可以分成三步：
     • 定义Model，比如$f(w)=w^{T}x+b$；
     • 寻找策略strategy，也就是定义Loss function；
     • 求解，寻找优化的方法，比如梯度下降(GD)，随机梯度下降(SGD)，牛顿法，拟牛顿法等等。
   • 贝叶斯派
     • 贝叶斯派的思想衍生出概率图模型。概率图模型重点研究的是Inferenc问题，$求一个后验概率分布P(Z|X)$，其中$X$为观测变量，$Z$为隐变量。
     • 实际上就是一个积分问题，因为贝叶斯框架中的归一化因子需要对整个状态空间进行积分，非常的复杂。代表性的有前面讲到的MCMC，MCMC的提出才是把贝叶斯理论代入到实际的运用中。
2. 概率图模型回顾
   1. 分类
      • 概率图模型，如果不考虑时序的关系，大致的分为：有向图的Bayesian Network和无向图的Markov Random Field (Markov Network)。
      • 根据分布获得的样本之间都是iid (独立同分布)的。比如Gaussian Mixture Model (GMM)，从$P(X|\theta )$的分布中采出N个样本$\{x_1,x_2,\cdots ,x_n\}$。N个样本之间都是独立同分布的。也就是对于隐变量$Z$，观测变量$X$之间，我们可以假设$P(X|Z)=\mathcal{N}(\mu ,\Sigma )$，这样就可以引入我们的先验信息，从而简化$X$的复杂分布。
   2. 动态模型
      对于采出$N$个样本$\{x_1,x_2,\cdots ,x_n\}$，如果引入了时间的信息，也就是$x_i$之间不再iid，我们称之为Dynamic Model。Dynamic Model拓扑结构图如下所示：

$$DynamicModel\{\begin{array}{c}离散\to HMM\\ 连续\to \{\begin{array}{c}线性\to KalmanFilter\\ 非线性\to ParticleFilter\end{array}\end{array}$$

14.1.2 HMM算法简介

1. 相关定义
   Hidden Markov Model的拓扑结构图如下所示：
   

   1. 拓扑结构图的第一行为$状态变量i$：$I=\{i_1,i_2,\cdots ,i_t,\cdots \}$，每个状态包含 $\mathcal{Q}=\{q_1,q_2,\cdots ,q_N\}$。其中$\mathcal{Q}$是状态变量$i$的$值域$，每个状态变量$i$可能有$N$个状态。
   2. 拓扑结构图的第二行为$观测变量o$：$O=\{o_1,o_2,\cdots ,o_t,\cdots \}$，每个状态包含 $\mathcal{V}=\{v_1,v_2,\cdots ,v_M\}$。其中$\mathcal{V}$是观察变量$o$的$值域$，每个观测变量$o_i$可能有$M$个状态。
   3. HMM可以看做一个三元组$\lambda =(\pi ,\mathcal{A},\mathcal{B})$。其中：
      • $\pi$：初始概率分布。
      • $\mathcal{A}$：状态转移矩阵。
      • $\mathcal{B}$：发射矩阵。

      1. $\mathcal{A}=[a_{ij}]$表示$状态转移矩阵$，$a_{ij}=P(i_{(i+1)}=q_j|i_{(t)}=q_i)$。$\mathcal{A}$表示为各个状态转移之间的概率。
      2. $\mathcal{B}=[b_j(k)]$表示$发射矩阵$，$b_j(k)=P(o_t=V_k|i_t=q_j)$。$\mathcal{B}$表示为观测变量和隐变量之间的关系。
      3. 而$\pi$是什么意思呢？假设当$t$时刻的隐变量$i_t$，可能有$\{q_1,q_2,\cdots ,q_N\}$个状态，而这些状态出现的概率分别为$\{p_1,p_2,\cdots ,p_N\}$。这就是一个关于$i_t$隐变量的离散随机分布。

2. 两个假设
   这是有关Hidden Markov Model的两个假设：
   齐次Markov假设(无后效性) 和 观察独立假设。

   1. $\text{齐次马尔可夫假设：}$
      未来与过去无关，只依赖与当前的状态。也就是：
      $$P(i_{t+1}|i_t,i_{t-1},\cdots ,i_1,o_t,\cdots ,o_1)=P(i_{t+1}|i_t)\text{\hspace{1em}(14.1.1)}$$
   2. $\text{观测独立假设：}$
      $$P(o_t|i_t,i_{t-1},\cdots ,i_1,o_t,\cdots ,o_1)=P(o_t|i_t)\text{\hspace{1em}(14.1.2)}$$

3. 三个问题

   1. Evaluation
      要求的问题就是$P(O|\lambda )$。也就是前向后向算法，给定一个模型$\lambda$，求出观测变量的概率分布。
   2. Learning
      $\lambda$如何求的问题。即：${\lambda }_{MLE}=\arg {\max }_{\lambda }P(O|\lambda )$。求解的方法是EM算法和Baum Welch算法。
   3. Decoding
      状态序列为$I$，$\hat{I}=\arg {\max }_{I}P(I|O,\lambda )$。也就是在在观测变量$O$和$\lambda$的情况下使隐变量序列$I$出现的概率最大。而这个问题大致被分为预测和滤波。
      • 预测问题为：$P(i_{t+1}|o_1,\cdots ,o_t)$；也就是在已知当前观测变量的情况下预测下一个状态，也就是Viterbi算法。
      • 滤波问题为：$P(i_t|o_1,\cdots ,o_t)$；也就是求$t$时刻的隐变量。

Hidden Markov Model，可以被我们总结成一个模型$\lambda =(\pi ,\mathcal{A},\mathcal{B})$，两个假设，三个问题。而其中关注最多的是Decoding的问题。

---

14.2 前向算法

14.2.1 概念回顾

图1

1. 序列和集合
   • $I=\{i_1,i_2,\cdots ,i_t,\cdots ,i_T\}\to 状态序列$，$\mathcal{Q}=\{q_1,q_2,\cdots ,q_N\}\to 状态值集合$。
   • $O=\{o_1,o_2,\cdots ,o_t,\cdots ,o_T\}\to 观测序列$，$\mathcal{V}=\{v_1,v_2,\cdots ,v_M\}\to 状态值集合$。
2. $\lambda =(\pi ,\mathcal{A},\mathcal{B})$
   • $\pi$：初始概率分布。$\pi =\{P_{(1)}(0),P_{(1)}(1),\cdots ,P_{(1)}(M)\}$。
   • $\mathcal{A}$：状态转移矩阵，$a_{ij}=P(i_{(i+1)}=q_j|i_{(t)}=q_i)$。
   • $\mathcal{B}$：发射矩阵，$b_j(k)=P(o_t=V_k|i_t=q_j)$。
3. 两个假设
   • $\text{齐次马尔可夫假设：}$ $P(i_{t+1}|i_t,i_{t-1},\cdots ,i_1,o_t,\cdots ,o_1)=P(i_{t+1}|i_t)$
   • $\text{观测独立假设：}$ $P(o_t|i_t,i_{t-1},\cdots ,i_1,o_t,\cdots ,o_1)=P(o_t|i_t)$
4. 三个问题
   • Evaluation：Given$\lambda$，求$P(O|\lambda )$。(Forward-Backward)
   • Learning: ${\lambda }_{MLE}=\arg {\max }_{\lambda }P(O|\lambda )$。(EM算法和Baum Welch算法)
   3. Decoding：$\hat{I}=\arg {\max }_{I}P(I|O,\lambda )$。(Viterbi)

本节主要是讲Evaluation中的Forward。

14.2.1 Evaluation-Forward

1. 基本方法
   • 对于$P(O|\lambda )$利用概率的基础知识进行化简：
     $$P(O|\lambda )=\sum _{I}P(O,I|\lambda )=\sum _{I}P(O|I,\lambda )P(I|\lambda )\text{\hspace{1em}(14.2.1)}$$
     其中：
     • ${\sum }_I$表示所有可能出现的隐状态序列；
     • ${\sum }_{I}P(O|I,\lambda )$表示在某个隐状态下，产生某个观测序列的概率；
     • $P(I|\lambda )$表示某个隐状态出现的概率。那么：
       $$\begin{array}{ll}P(I|\lambda )& =P(i_1,\cdots ,i_T|\lambda )\\ & =P(i_T|i_1,\cdots ,i_{T-1},\lambda )\cdot P(i_1,\cdots ,i_{T-1}|\lambda )\end{array}\text{\hspace{1em}(14.2.2)}$$
   • 根据Hidden Markov Model两个假设
     • 齐次马尔可夫假设，可得：$P(i_T|i_1,\cdots ,i_{T-1},\lambda )=P(i_T|i_{T-1})=a_{i_{T-1},i_T}$。对公式(14.2.2)进行化简可以得到：
       $$\begin{array}{ll}P(i_T|i_1,\cdots ,i_{T-1},\lambda )\cdot P(i_1,\cdots ,i_{T-1}|\lambda )& =P(i_T|i_{T-1})\cdot P(i_1,\cdots ,i_{T-1}|\lambda )\\ & =a_{i_{T-1},i_T}\cdot a_{i_{T-2},i_{T-1}}\cdots a_{i_1,i_2}\cdot \pi (a_{i_1})\\ & =\pi (a_{i_1}){\prod }_{t=2}^T{a}_{i_{t-1},i_t}\end{array}\text{\hspace{1em}(14.2.3)}$$
     • 观察独立假设，可知：
       $$\begin{array}{ll}P(O|I,\lambda )& =P(o_1,o_2,\cdots ,o_T|I,\lambda )\\ & ={\prod }_{t=1}^{T}P(o_t|I,\lambda )\\ & ={\prod }_{t=1}^T{b}_{i_t}(o_t)\end{array}\text{\hspace{1em}(14.2.4)}$$
   3. 结合公式(14.2.4)和(14.2.3)，(14.2.1)可以化简为：
      $$\begin{array}{ll}P(O|\lambda )& ={\sum }_I\pi (a_{i_1}){\prod }_{t=2}^T{a}_{i_{t-1},i_t}{\prod }_{t=1}^T{b}_{i_t}(o_t)\\ & ={\sum }_{i_1}\cdot {\sum }_{i_2}\cdots {\sum }_{i_T}\pi (a_{i_1}){\prod }_{t=2}^T{a}_{i_{t-1},i_t}{\prod }_{t=1}^T{b}_{i_t}(o_t)\end{array}\text{\hspace{1em}(14.2.5)}$$
      公式(14.2.1)共有$T$个状态，每个状态有$N$种可能，所以算法复杂度为$\mathcal{O}(N^T)$。计算太困难了！
2. Forward Algorithm
   下图是Hidden Markov Model的拓扑结构图：
   
   1. 思路
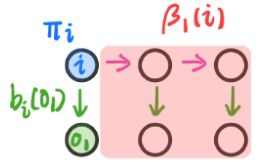
      我们记${\alpha }_t(i)=P(o_1,\cdots ,o_t,i_t=q_i|\lambda )$，这个公式表示：在之前所有的观测变量的前提下求出当前时刻的隐变量的概率。那么：
      $$P(O|\lambda )=\sum _{i=1}^{N}P(O,i_T=q_i|\lambda )=\sum _{i=1}^N{\alpha }_T(i)\text{\hspace{1em}(14.2.6)}$$
      其中，${\sum }_{i=1}^N$表示对所有可能出现的隐状态情形求和。通过寻找${\alpha }_t(i)$和${\alpha }_t(i+1)$之间的递推关系，就可以得到整个观测序列出现的概率。
   2. 求解递推关系
      ${\alpha }_t(i+1)$可以写成：
      $${\alpha }_t(i+1)=P(o_1,\cdots ,o_t,o_{t+1},i_{t+1}=q_j|\lambda )\text{\hspace{1em}(14.2.7)}$$
      因为${\alpha }_t(i)$里面有$i_t=q_j$，因此想办法把$i_t$给塞进${\alpha }_t(i+1)$中，即：
      $$\begin{array}{ll}{\alpha }_t(i+1)& =P(o_1,\cdots ,o_t,o_{t+1},i_{t+1}=q_j|\lambda )\\ & ={\sum }_{i=1}^{N}P(o_1,\cdots ,o_t,o_{t+1},i_t=q_i,i_{t+1}=q_j|\lambda )\\ & ={\sum }_{i=1}^{N}P(o_{t+1}|o_1,\cdots ,o_t,i_t=q_i,i_{t+1}=q_j,\lambda )\cdot P(o_1,\cdots ,o_t,i_t=q_i,i_{t+1}=q_j|\lambda )\end{array}\text{\hspace{1em}(14.2.7)}$$
      • 根据观测独立性假设，可得$P(o_{t+1}|o_1,\cdots ,o_t,i_t=q_i,i_{t+1}=q_j,\lambda )=P(o_{t+1}|i_{t+1}=q_j)$。所以：
        $$\begin{array}{ll}{\alpha }_t(i+1)& ={\sum }_{i=1}^{N}P(o_{t+1}|o_1,\cdots ,o_t,i_t=q_i,i_{t+1}=q_j,\lambda )\cdot P(o_1,\cdots ,o_t,i_t=q_i,i_{t+1}=q_j|\lambda )\\ & ={\sum }_{i=1}^{N}P(o_{t+1}|i_{t+1}=q_j)\cdot P(o_1,\cdots ,o_t,i_t=q_i,i_{t+1}=q_j|\lambda )\end{array}\text{\hspace{1em}(14.2.8)}$$
        看到这个化简后的公式，与${\alpha }_t(i)$相比，还多了一项$i_{t+1}=q_j$，下一步的工作就是消去它。所以：
        $$P(o_1,\cdots ,o_t,i_t=q_i,i_{t+1}=q_j|\lambda )=P(i_{t+1}=q_j|o_1,\cdots ,o_t,i_t=q_i,\lambda )\cdot P(o_1,\cdots ,o_t,i_t=q_i|\lambda )\text{\hspace{1em}(14.2.9)}$$
      • 根据齐次马尔可夫性质，可得$P(i_{t+1}=q_j|o_1,\cdots ,o_t,i_t=q_i,\lambda )=P(i_{t+1}=q_j|i_t=q_i)$。所以：
        $$\begin{array}{ll}{\alpha }_{t+1}(j)& ={\sum }_{i=1}^{N}P(o_{t+1}|i_{t+1}=q_j)\cdot P(i_{t+1}=q_j|i_t=q_i)\cdot P(o_1,\cdots ,o_t,i_t=q_i|\lambda )\\ & ={\sum }_{i=1}^N{b}_j(o_{t+1})\cdot a_{ij}\cdot {\alpha }_t(i)\end{array}\text{\hspace{1em}(14.2.10)}$$
      • 经过上述的推导，我们就成功的得到了${\alpha }_{t+1}(j)$和${\alpha }_t(i)$之间的关系：
        $${\alpha }_{t+1}(j)=\sum _{i=1}^N{b}_j(o_{t+1})\cdot a_{ij}\cdot {\alpha }_t(i)\text{\hspace{1em}(14.2.11)}$$
        通过这个递推关系，就可以遍历整个Markov Model了。这个公式是什么意思呢？它可以表达为，所有可能出现的隐变量状态乘以转移到状态$j$的概率，乘以根据隐变量$i_{t+1}$观察到$o_{t+1}$的概率，乘上根据上一个隐状态观察到的观察变量的序列的概率。
3. 总结
   
   $$\begin{gathered} 令{\alpha }_t(i)=P(o_1,\cdots ,o_t,i_t=q_i|\lambda ) \\ P(O|\lambda )=\sum _{i=1}^{N}P(O,i_t=q_i|\lambda )=\sum _{i=1}^N{\alpha }_T(i) \\ {\alpha }_{t+1}(j)=\sum _{i=1}^N{b}_j(o_{t+1})\cdot a_{ij}\cdot {\alpha }_t(i) \end{gathered}$$
   用一个图来进行表示：
   假设有隐状态的状态空间数为$N$，序列的长度为$T$，那么总的时间复杂度为$\mathcal{O}(T{N}^2)$。

---

14.3 后向算法

后向概率的推导实际上比前向概率的理解要难，前向算法是一个联合概率，而后向算法则是一个条件概率，所以后向的概率实际上比前向难求很多。

1. 基本思路
   下图是Hidden Markov Model的拓扑结构图：
   
   定义：
   $${\beta }_t(i)=P(o_{t+1},\cdots ,o_T|i_t=q_i,\lambda )\text{\hspace{1em}(14.3.1)}$$
   则${\beta }_1(t)=P(o_2,\cdots ,o_T|i_1=q_i,\lambda )$。计算目标$P(O|\lambda )$可以表示为：：
   $$\begin{array}{ll}P(O|\lambda )& =P(o_1,\cdots ,o_T|\lambda )\\ & ={\sum }_{i=1}^{N}P(o_1,\cdots ,o_T,i_1=q_i|\lambda )\\ & ={\sum }_{i=1}^{N}P(o_1,\cdots ,o_T|i_1=q_i,\lambda )\underset{{\pi }_i}{P(i_1=q_i|\lambda )}\\ & ={\sum }_{i=1}^{N}P(o_1|o_2,\cdots ,o_T,i_1=q_i,\lambda )\underset{{\beta }_1(i)}{P(o_2,\cdots ,o_T|i_1=q_i,\lambda )}{\pi }_i\\ & ={\sum }_{i=1}^{N}P(o_1|i_1=q_i,\lambda ){\beta }_1(i){\pi }_i\\ & ={\sum }_{i=1}^N{b}_i(o_1){\beta }_1(i){\pi }_i\end{array}\text{\hspace{1em}(14.3.2)}$$
   现在已成功的找到$P(O|\lambda )和第一个状态之间的关系$。其中：

   • ${\pi }_i$为某个状态的初始状态的概率；
   • $b_i(o_1)$表示为第$i$个隐变量产生第1个观测变量的概率；
   • ${\beta }_1(i)$表示为第一个观测状态确定以后生成后面观测状态序列的概率。结构图如下所示：
     

2. 求解递推关系
   因此如果我们能找到${\beta }_t(i)$到${\beta }_{t+1}(j)$的递推式，就可以由通过递推得到${\beta }_1(i)$，从而计算$P(O|\lambda )$，则递推公式是：
   $$\begin{array}{ll}{\beta }_t(i)& =P(o_{t+1},\cdots ,o_T|i_t=q_i,\lambda )\\ & ={\sum }_{j=1}^{N}P(o_{t+1},\cdots ,o_T,i_{t+1}=q_j|i_t=q_i,\lambda )\\ & ={\sum }_{j=1}^{N}P(o_{t+1},\cdots ,o_T|i_{t+1}=q_j,i_t=q_i,\lambda )P(i_{t+1}=q_j|i_t=q_i,\lambda )\\ & ={\sum }_{j=1}^{N}P(o_{t+1},\cdots ,o_T|i_{t+1}=q_j,\lambda )a_{ij}\\ & ={\sum }_{j=1}^{N}P(o_{t+1}|o_{t+2},\cdots ,o_T,i_{t+1}=q_j,\lambda )P(o_{t+2},\cdots ,o_T|i_{t+1}=q_j,\lambda )a_{ij}\\ & (从这一步到下一步满足:A\perp C|B\iff 若B被观测，则路径被阻塞。)\\ & ={\sum }_{j=1}^{N}P(o_{t+1}|i_{t+1}=q_j,\lambda ){\beta }_{t+1}(j)a_{ij}\\ & ={\sum }_{j=1}^N{b}_j(o_{t+1})a_{ij}{\beta }_{t+1}(j)\end{array}\text{\hspace{1em}(14.3.3)}$$
   其中第五行到第六行的推导$P(o_{t+1},\cdots ,o_T|i_{t+1}=q_j,i_t=q_i)=P(o_{t+1},\cdots ,o_T|i_{t+1}=q_j)$使用的马尔可夫链的性质，每一个状态都是后面状态的充分统计量，与之前的状态无关。
   

3. 总结
   

   $$\begin{gathered} 定义：{\beta }_t(i)=P(o_{t+1},\cdots ,o_T|i_t=q_i,\lambda ) \\ P(O|\lambda )=\sum _{i=1}^N{b}_i(o_1){\beta }_1(i){\pi }_i \\ {\beta }_t(i)=\sum _{j=1}^N{b}_j(o_{t+1})a_{ij}{\beta }_{t+1}(j)\text{\hspace{1em}(14.3.4)} \end{gathered}$$
   通过这样的迭代从后往前推，我们就可以得到${\beta }_i(1)$的概率，从而推断出$P(O|\lambda )$。整体的推断流程图如下图所示：
   
   这就是后向算法，其复杂度也为$O(T{N}^2)$。

---

14.4 Beco Decoding算法(Learning)

14.4.1 问题简化

• 上两节讲的是HMM的Evaluating部分，接下来讲HMM的Learning部分。即目标是：$在已知观测数据的情况下求参数\lambda$：
  $${\lambda }_{MLE}=\arg \underset{\lambda }{\max }P(O|\lambda )\text{\hspace{1em}(14.4.1)}$$
  因为：
  $$P(O|\lambda )=\sum _{I}P(O,I|\lambda )=\sum _{i_1}\cdots \sum _{i_T}{\pi }_{i_1}\prod _{t=2}^T{a}_{i_{t-1},i_t}\prod _{t=1}^T{b}_{i_1}(o_t)\text{\hspace{1em}(14.4.2)}$$
  对这个方程的$\lambda$求偏导，实在是太难算了。
• 问题简化
  所以考虑使用EM算法。先来回顾一下EM算法：
  $${\theta }^{(t+1)}=\arg \underset{\theta }{\max }{\int }_z\log P(X,Z|\theta )\cdot P(Z|X,{\theta }^{(t)})dZ\text{\hspace{1em}(14.4.3)}$$
  其中：
  • $X\to O$为观测变量；
  • $Z\to I$为隐变量，其中$I$为离散变量；
  • $\theta \to \lambda$为参数。
    那么，可以将公式（14.4.3）改写为：
    $${\lambda }^{(t+1)}=\arg \underset{\lambda }{\max }\sum _I\log P(O,I|\lambda )\cdot P(I|O,{\lambda }^{(t)})\text{\hspace{1em}(14.4.4)}$$
    每次迭代${\lambda }^{(t+1)}$，${\lambda }^{(t)}$是一个常数，即：
    $$P(I|O,{\lambda }^{(t)})=\frac{P(I,O|{\lambda }^{(t)})}{P(O|{\lambda }^{(t)})}\text{\hspace{1em}(14.4.5)}$$
    并且$P(O|{\lambda }^{(t)})$中${\lambda }^{(t)}$是常数，所以这项是个定量，与$\lambda$无关，所以$\frac{P(I,O|{\lambda }^{(t)})}{P(O|{\lambda }^{(t)})}\propto P(I,O|{\lambda }^{(t)})$。所以等式(14.4.4)改写为：
    $${\lambda }^{(t+1)}=\arg \underset{\lambda }{\max }\sum _I\log P(O,I|\lambda )\cdot P(I,O|{\lambda }^{(t)})\text{\hspace{1em}(14.4.6)}$$
    其中${\lambda }^{(t)}=({\pi }^{(t)},{\mathcal{A}}^{(t)},{\mathcal{B}}^{(t)})$，而${\lambda }^{(t+1)}=({\pi }^{(t+1)},{\mathcal{A}}^{(t+1)},{\mathcal{B}}^{(t+1)})$。这样做有什么目的呢？可以把$\log P(O,I|\lambda )$和$P(I,O|{\lambda }^{(t)})$变成一种形式。
• 公式优化
  对于公式(14.4.6)，定义：
  $$Q(\lambda ,{\lambda }^{(t)})=\sum _I\log P(O,I|\lambda )\cdot P(O,I|{\lambda }^{(t)})\text{\hspace{1em}(14.4.7)}$$
  因为公式(14.4.2)化简可知：$P(O,I|\lambda )={\pi }_{i_1}{\prod }_{t=2}^T{a}_{i_{t-1},i_t}{\prod }_{t=1}^T{b}_{i_1}(o_t)$。所以：
  $$Q(\lambda ,{\lambda }^{(t)})=\sum _I\left[\left(\log {\pi }_{i_1}+\sum _{t=2}^T\log a_{i_{t-1},i_t}+\sum _{t=1}^T\log b_{i_t}(o_t)\right)\cdot P(O,I|{\lambda }^{(t)})\right]\text{\hspace{1em}(14.4.8)}$$

14.4.2 求解最优值

• 以${\pi }^{(t+1)}$为例，在公式$Q(\lambda ,{\lambda }^{(t)})$中，${\sum }_{t=2}^T\log a_{i_{t-1},i_t}$与${\sum }_{t=1}^T\log b_{i_t}(o_t)$与$\pi$无关，所以，
  $$\begin{array}{ll}{\pi }^{(t+1)}& =\arg {\max }_{\pi }Q(\lambda ,{\lambda }^{(t)})\\ & =\arg {\max }_{\pi }{\sum }_I[\log {\pi }_{i_1}\cdot P(O,I|{\lambda }^{(t)})]\\ & =\arg {\max }_{\pi }{\sum }_{i_1}\cdots {\sum }_{i_T}[\log {\pi }_{i_1}\cdot P(O,i_1,\cdots ,i_T|{\lambda }^{(t)})]\end{array}\text{\hspace{1em}(14.4.9)}$$
  观察$\{i_2,\cdots ,i_T\}$可知，$联合概率分布求和可以得到边缘概率$。所以：
  $$\begin{array}{ll}{\pi }^{(t+1)}& =\arg {\max }_{\pi }{\sum }_{i_1}[\log {\pi }_{i_1}\cdot P(O,i_1|{\lambda }^{(t)})]\\ & =\arg {\max }_{\pi }{\sum }_{i=1}^N[\log {\pi }_i\cdot P(O,i_1=q_i|{\lambda }^{(t)})]\end{array}\text{\hspace{1em}(14.4.10)}$$
  优化问题可以描述为：
  $$\{\begin{array}{l}{\pi }^{(t+1)}=\underset{\pi }{\mathrm{argmax}}{\sum }_{i=1}^N[\log {\pi }_i\cdot P(O,i_1=q_i|{\lambda }^{(t)})]\\ s.t.{\sum }_{i=1}^N{\pi }_i=1\end{array}\text{\hspace{1em}(14.4.11)}$$
• 拉格朗日乘子法求解
  根据拉格朗日乘子法，我们可以将损失函数写完：
  $$\mathcal{L}(\pi ,\eta )=\sum _{i=1}^N\log {\pi }_i\cdot P(O,i_1=q_i|{\lambda }^{(t)})+\eta (\sum _{i=1}^N{\pi }_i-1)\text{\hspace{1em}(14.4.12)}$$
  使似然函数最大化，则是对损失函数$\mathcal{L}(\pi ,\eta )$求偏导，则为：
  $$\begin{array}{ll}& \frac{\mathcal{L}}{{\pi }_i}=\frac{1}{{\pi }_i}P(O,i_1=q_i|{\lambda }^{(t)})+\eta =0\\ & P(O,i_1=q_i|{\lambda }^{(t)})+{\pi }_i\eta =0\end{array}\text{\hspace{1em}(14.4.13)}$$
  又因为 ∑ i = 1 N π i = 1 \sum_{i=1}^N \pi_i = 1 ∑i=1N​π