策略梯度算法的理解

---

前言

策略梯度(Policy Gradient, PG)的通俗介绍。

---

一、来源？

1. DQN

深度学习是监督学习，需要有标签数据来计算损失函数，通过梯度下降和误差反向传播来更新神经网络的参数，那在强化学习中如何获得标签呢？
Q-learning：$$Q\left(S_t,A_t\right)\leftarrow Q\left(S_t,A_t\right)+\alpha \left[R_{t+1}+\gamma \underset{a}{\max }Q\left(S_{t+1},a\right)-Q\left(S_t,A_t\right)\right]$$

$$R_{t+1}+\gamma \underset{a}{\max }Q\left(S_{t+1},a;\theta \right)$$
用神经网络拟合Q学习中的误差项，使其$$L\left(\theta \right)=E\left({\left(R+\underset{a}{\max }Q\left(s,a,\theta \right)-Q\left(s,a,\theta \right)\right)}^2\right)$$
最小化。这里括号内的$$R_t+\gamma \underset{a}{\max }Q\left(S_t,a;\theta \right)$$ 近似$$Q\left(s,a,\theta \right)$$ 即可最大程度上使前文标签合理化，因此之后的改进也是围绕这点进行的。

2 DQN的不足

深度学习需要大量带标签的训练数据；
强化学习从 scalar reward 进行学习，但是 reward 经常是 sparse,
noisy, delayed； 深度学习假设样本数据是独立同分布的，但是强化学习中采样的数据是强相关的。

因此，DQN 采用经验回放（Experience Replay）机制，将训练过的数据进行储存到 Replay Buffer 中，以便后续从中随机采样进行训练，好处就是：1. 数据利用率高；2. 减少连续样本的相关性，从而减小方差（variance）。

Nature 2015 中 DQN 做了改进，提出了一个目标网络$$Q\left(S_{t+1},a;{\theta }^{-}\right)$$ 每经过 N 个回合的迭代训练，将$$Q\left(S_{t+1},a;\theta \right)$$ 的参数复制给目标网络$$Q\left(S_{t+1},a;{\theta }^{-}\right)$$


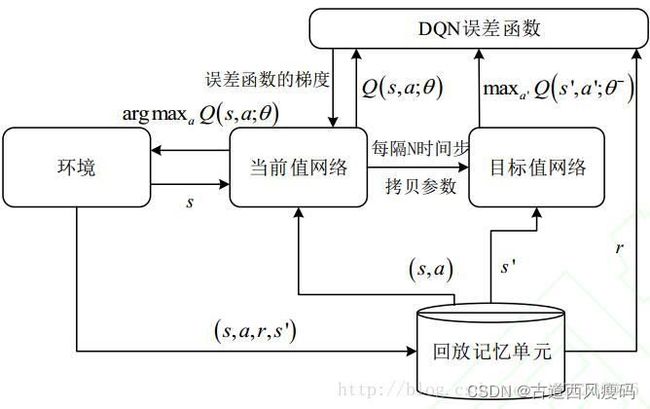
DQN虽然在某些问题上取得了成功，但存在以下问题：

1.无法表示随机策略，某些问题的最优策略是随机策略，需要以不同的概率选择不同的动作。而DQN之类的算法在实现时采用了 贪心策略$$\underset{a}{\max }Q\left(S_t,a;\theta \right)$$，显然无法实现这种按照概率执行各种候选动作的要求。
2.这种方法输出值（各个动作的最优Q函数值）的微小改变会导致某一动作被选中或不选中，这种不连续的变化会影响算法的收敛。这很容易理解，假设一个动作a的Q函数值本来在所有动作中是第2大的，把它增加0.0001，就变成第最大的，那这种微小的变化会导致策略完全改变。因为之前它不是最优动作，现在变成最优动作了。
3.无法表示连续动作。DQN要求动作空间是离散的，且只能是有限个。某些问题中，动作是连续的，例如要控制在x y z方向的速度、加速度，这些值显然是连续的。

二、策略梯度

1.区别

PG让神经网络直接输出策略函数 π(s)，即在状态s下应该执行何种动作。对于非确定性策略，输出的是这种状态下执行各种动作的概率值，即如下的条件概率：
$$\pi \left(a|s\right)=p\left(a|s\right)$$
对于PG，其输出的是每种动作的概率，而不是DQN中的Q值，从而使每种动作选择的概率是确定的，因此是确定性策略。
此时的神经网络输出层的作用类似于多分类问题的softmax回归，输出的是一个概率分布，只不过这里的概率分布不是用来进行分类，而是执行动作。至于对于连续型的动作空间该怎么处理，我们在后面会解释。
因此，如果构造出了一个目标函数L，其输入是神经网络输出的策略函数$$\pi (a|s)$$.这可以通过梯度上升法实现（与梯度下降法相反，向着梯度方向迭代，用于求函数的极大值）。训练时的迭代公式为$${\theta }_{t+1}={\theta }_t+\alpha {\nabla }_{\theta }L\left({\theta }_t\right)$$
这里假设策略函数对参数的梯度$${\nabla }_0\pi \left(a|s;\theta \right)$$ 存在，从而保证$${\nabla }_{\theta }L\left({\theta }_t\right)$$现在问题的核心就是
(1)如何构造这种目标函数L
(2)如何生成训练样本。
对于后者，采用了与DQN类似的思路，即按照当前策略随机地执行动作，并观察其回报值，以生成样本。
对于第一个问题，一个自然的想法是使得按照这种策略执行时的累计回报最大化，即构造出类似V函数和Q函数这样的函数来。下面介绍常用的目标函数。

2.目标函数构造

第一种称为平均奖励（average reward）目标函数，用于没有结束状态和起始状态的问题。它定义为各个时刻回报值的均值，是按照策略π执行，时间长度n趋向于+∞时回报均值的极限：
$$L\left(\pi \right)=\underset{n\to +\infty }{\lim }\frac{1}{n}E\left[r_1+r_2+\cdots +r_n|\pi \right]=\sum _s{p}_{\pi }\left(s\right)\sum _a\pi \left(a|s\right)R\left(a,s\right)$$ 其中，ri为即时回报，p(s)是状态s的平稳分布，定义为按照策略π执行时该状态出现的概率，
$$\sum _a\pi \left(a|s\right)R\left(a,s\right)$$ 则为在状态s下执行各种动作时得到的立即回报的均值，R(a,s)为在状态s下执行动作a所得到的立即回报的数学期望。
$$R\left(s,a\right)=E\left[r_{t+1}|s_t=s,a_t=a\right]$$ 平稳分布是如下的极限
$$p_{\pi }\left(s\right)=\underset{t\to +\infty }{\lim }p\left(s_t=s|s_0,\pi \right)$$ 其意义为按照策略π执行，当时间t趋向于+∞时状态s出现的概率。这是随机过程中的一个概念，对于马尔可夫链，如果满足一定的条件，则无论起始状态的概率分布（即处于每种状态的概率）是怎样的，按照状态转移概率进行演化，系统最后会到达平稳分布，在这种情况下，系统处于每种状态的概率是稳定的。

总结

代码来自于莫烦强化学习教程：Tutorial，Code

class DeepQNetwork:
    def __init__(
            self,
            n_actions,
            n_features,
            learning_rate=0.01,
            reward_decay=0.9,
            e_greedy=0.9,
            replace_target_iter=300,
            memory_size=500,
            batch_size=32,
            e_greedy_increment=None,
            output_graph=False,
    ):
        self.n_actions = n_actions
        self.n_features = n_features
        self.lr = learning_rate
        self.gamma = reward_decay
        self.epsilon_max = e_greedy
        self.replace_target_iter = replace_target_iter
        self.memory_size = memory_size
        self.batch_size = batch_size
        self.epsilon_increment = e_greedy_increment
        self.epsilon = 0 if e_greedy_increment is not None else self.epsilon_max

        # total learning step
        self.learn_step_counter = 0

        # initialize zero memory [s, a, r, s_]
        self.memory = np.zeros((self.memory_size, n_features * 2 + 2))

        # consist of [target_net, evaluate_net]
        self._build_net()
        t_params = tf.get_collection('target_net_params')
        e_params = tf.get_collection('eval_net_params')
        self.replace_target_op = [tf.assign(t, e) for t, e in zip(t_params, e_params)]

        self.sess = tf.Session()

        if output_graph:
            # $ tensorboard --logdir=logs
            tf.summary.FileWriter("logs/", self.sess.graph)

        self.sess.run(tf.global_variables_initializer())
        self.cost_his = []

    def _build_net(self):
        # ------------------ build evaluate_net ------------------
        self.s = tf.placeholder(tf.float32, [None, self.n_features], name='s')  # input
        self.q_target = tf.placeholder(tf.float32, [None, self.n_actions], name='Q_target')  # for calculating loss
        with tf.variable_scope('eval_net'):
            # c_names(collections_names) are the collections to store variables
            c_names = ['eval_net_params', tf.GraphKeys.GLOBAL_VARIABLES] 
            n_l1 = 10
            w_initializer = tf.random_normal_initializer(0., 0.3)
            b_initializer = tf.constant_initializer(0.1)

            # first layer. collections is used later when assign to target net
            with tf.variable_scope('l1'):
                w1 = tf.get_variable('w1', [self.n_features, n_l1], initializer=w_initializer, collections=c_names)
                b1 = tf.get_variable('b1', [1, n_l1], initializer=b_initializer, collections=c_names)
                l1 = tf.nn.relu(tf.matmul(self.s, w1) + b1)

            # second layer. collections is used later when assign to target net
            with tf.variable_scope('l2'):
                w2 = tf.get_variable('w2', [n_l1, self.n_actions], initializer=w_initializer, collections=c_names)
                b2 = tf.get_variable('b2', [1, self.n_actions], initializer=b_initializer, collections=c_names)
                self.q_eval = tf.matmul(l1, w2) + b2

        with tf.variable_scope('loss'):
            self.loss = tf.reduce_mean(tf.squared_difference(self.q_target, self.q_eval))
        with tf.variable_scope('train'):
            self._train_op = tf.train.RMSPropOptimizer(self.lr).minimize(self.loss)

        # ------------------ build target_net ------------------
        self.s_ = tf.placeholder(tf.float32, [None, self.n_features], name='s_')    # input
        with tf.variable_scope('target_net'):
            # c_names(collections_names) are the collections to store variables
            c_names = ['target_net_params', tf.GraphKeys.GLOBAL_VARIABLES]

            # first layer. collections is used later when assign to target net
            with tf.variable_scope('l1'):
                w1 = tf.get_variable('w1', [self.n_features, n_l1], initializer=w_initializer, collections=c_names)
                b1 = tf.get_variable('b1', [1, n_l1], initializer=b_initializer, collections=c_names)
                l1 = tf.nn.relu(tf.matmul(self.s_, w1) + b1)

            # second layer. collections is used later when assign to target net
            with tf.variable_scope('l2'):
                w2 = tf.get_variable('w2', [n_l1, self.n_actions], initializer=w_initializer, collections=c_names)
                b2 = tf.get_variable('b2', [1, self.n_actions], initializer=b_initializer, collections=c_names)
                self.q_next = tf.matmul(l1, w2) + b2

    def store_transition(self, s, a, r, s_):
        if not hasattr(self, 'memory_counter'):
            self.memory_counter = 0

        transition = np.hstack((s, [a, r], s_))

        # replace the old memory with new memory
        index = self.memory_counter % self.memory_size
        self.memory[index, :] = transition

        self.memory_counter += 1

    def choose_action(self, observation):
        # to have batch dimension when feed into tf placeholder
        observation = observation[np.newaxis, :]

        if np.random.uniform() < self.epsilon:
            # forward feed the observation and get q value for every actions
            actions_value = self.sess.run(self.q_eval, feed_dict={self.s: observation})
            action = np.argmax(actions_value)
        else:
            action = np.random.randint(0, self.n_actions)
        return action

    def learn(self):
        # check to replace target parameters
        if self.learn_step_counter % self.replace_target_iter == 0:
            self.sess.run(self.replace_target_op)
            print('\ntarget_params_replaced\n')

        # sample batch memory from all memory
        if self.memory_counter > self.memory_size:
            sample_index = np.random.choice(self.memory_size, size=self.batch_size)
        else:
            sample_index = np.random.choice(self.memory_counter, size=self.batch_size)
        batch_memory = self.memory[sample_index, :]

        q_next, q_eval = self.sess.run(
            [self.q_next, self.q_eval],
            feed_dict={
                self.s_: batch_memory[:, -self.n_features:],  # fixed params
                self.s: batch_memory[:, :self.n_features],  # newest params
            })

        # change q_target w.r.t q_eval's action
        q_target = q_eval.copy()

        batch_index = np.arange(self.batch_size, dtype=np.int32)
        eval_act_index = batch_memory[:, self.n_features].astype(int)
        reward = batch_memory[:, self.n_features + 1]

        q_target[batch_index, eval_act_index] = reward + self.gamma * np.max(q_next, axis=1)

        """
        For example in this batch I have 2 samples and 3 actions:
        q_eval =
        [[1, 2, 3],
         [4, 5, 6]]

        q_target = q_eval =
        [[1, 2, 3],
         [4, 5, 6]]

        Then change q_target with the real q_target value w.r.t the q_eval's action.
        For example in:
            sample 0, I took action 0, and the max q_target value is -1;
            sample 1, I took action 2, and the max q_target value is -2:
        q_target =
        [[-1, 2, 3],
         [4, 5, -2]]

        So the (q_target - q_eval) becomes:
        [[(-1)-(1), 0, 0],
         [0, 0, (-2)-(6)]]

        We then backpropagate this error w.r.t the corresponding action to network,
        leave other action as error=0 cause we didn't choose it.
        """

        # train eval network
        _, self.cost = self.sess.run([self._train_op, self.loss],
                                     feed_dict={self.s: batch_memory[:, :self.n_features],
                                                self.q_target: q_target})
        self.cost_his.append(self.cost)

        # increasing epsilon
        self.epsilon = self.epsilon + self.epsilon_increment if self.epsilon < self.epsilon_max else self.epsilon_max
        self.learn_step_counter += 1