使用1维物体的相机标定 camera calibration with one-dimensional objects

使用1维物体的相机标定 camera calibration with one-dimensional objects

张正友2004年PAMI的文章，不同于二维标定板，使用一维线段进行标定。

---

张博士这篇文章使用的相机模型与之前富有盛名的张氏标定的相机模型相同。（2000年PAMI A Flexible New Technique
for Camera Calibration）

sm¯¯¯¯¯=A[R,t]M¯¯¯¯¯ s m ¯ = A [ R , t ] M ¯

s是尺度因子（深度信息Z），A是内参数矩阵，R，t外参数矩阵， m¯¯¯¯¯ m ¯ 是齐次图像坐标(u,v,1)， M¯¯¯¯¯ M ¯ 是写作了非齐次世界坐标(x,y,z)。

在正式介绍他的做法前，先分析了几种可能的标定情况。

Setups with Free-Moving 1D Calibration Objects

（1）Two points with known distance.
假设线段两端点为A，B。则需要5个参数去描述（define）它们。因为3个参数先定下A，在已知AB长度的情况下，B是在一个球面上运动，只再需要2个参数可以确定B。（原文说的是确定AB朝向只需要两个参数，扯远点可以认为B是一个二维变量嵌入在三维空间的流形。^-^突然想到这个）而每个图像点提供两个方程，一共四个方程。假设观测N次则有5N个点的位置参数和5个内参数，一共 5N+5 5 N + 5 个待求参数，却只有 4N 4 N 个等式，显然不能求解。

（2）Three collinear points with known distances.
加入一点C，知道C与A，B的距离，同样N次观测，所以待求参数仍为 5N+5 5 N + 5 。但由于ABC三点共线，AB一起提供4N个方程，C由于非线性独立，只能再多提供N个方程，一共 5N 5 N 个等式，所以无法求解。

（3）Four or more collinear points with known distances.
熟悉摄影定理的同学一定知道交比定理，第四个点所提供的信息时刻都成立，被前三个所包含，所以显然再加进去一个点对求解无益。

Setups with 1D Calibration Objects Moving Around a Fixed Point

通过上面的讨论如果让线段任意移动是无法实现标定的，所以张博士就让其中一点固定下来不动！（￥-￥）

（1）Two points with known distance.
把A fixed下来 moving B，这样每次观测只需要两个参数就可以描述AB，于是N次观测下待求参数有 5+3+2N 5 + 3 + 2 N 。但是每次能提供的方程却只有 2+2N 2 + 2 N ，所以还是不能求解。

（2）Three collinear points with known distances.
三个点的情况下待求参数还是 8+2N 8 + 2 N ，但能提供的方程已经是 2+3N 2 + 3 N ，所以是可以求解了，需要使 2+3N>8+2N 2 + 3 N > 8 + 2 N 则 N>6 N > 6 意味着最少要有六次观测。

（3）Four or more collinear points with known distances.
再多的点已经信息冗余了，但在图像有噪声的情况下，更多的点做最小二乘可以提高标定的精度。

封闭解的解法 Closed-Form Solution

已知如下

||B−A||=L | | B − A | | = L

C=λAA+λBB C = λ A A + λ B B

我们选择相机坐标系就是世界坐标系，此时 R=I,t=0 R = I , t = 0 则

A=zAA−1a¯¯¯ A = z A A − 1 a ¯

B=zBB−1b¯¯ B = z B B − 1 b ¯

C=zCC−1c¯¯ C = z C C − 1 c ¯

将它们代入已知的上式可得

zCc¯¯=zAλAa¯¯¯+zBλBb¯¯ z C c ¯ = z A λ A a ¯ + z B λ B b ¯

两边同时叉乘向量 c¯¯ c ¯ 则有

zAλA(a¯¯¯×c¯¯)+zBλB(b¯¯×c¯¯)=0 z A λ A ( a ¯ × c ¯ ) + z B λ B ( b ¯ × c ¯ ) = 0

因此

zB=−zAλA(a¯¯¯×c¯¯)⋅(b¯¯×c¯¯)λB(b¯¯×c¯¯)⋅(b¯¯×c¯¯) z B = − z A λ A ( a ¯ × c ¯ ) ⋅ ( b ¯ × c ¯ ) λ B ( b ¯ × c ¯ ) ⋅ ( b ¯ × c ¯ )

根据 ||A−B||=L | | A − B | | = L 可得

||A−1(zBb¯¯−zAa¯¯¯)||=L | | A − 1 ( z B b ¯ − z A a ¯ ) | | = L

zA||A−1(a¯¯¯+λA(a¯¯¯×c¯¯)⋅(b¯¯×c¯¯)λB(b¯¯×c¯¯)⋅(b¯¯×c¯¯)b¯¯)||=L z A | | A − 1 ( a ¯ + λ A ( a ¯ × c ¯ ) ⋅ ( b ¯ × c ¯ ) λ B ( b ¯ × c ¯ ) ⋅ ( b ¯ × c ¯ ) b ¯ ) | | = L

这等价于

z2AhTA−TA−1h=L2 z A 2 h T A − T A − 1 h = L 2

其中

h=a¯¯¯+λA(a¯¯¯×c¯¯)⋅(b¯¯×c¯¯)λB(b¯¯×c¯¯)⋅(b¯¯×c¯¯)b¯¯ h = a ¯ + λ A ( a ¯ × c ¯ ) ⋅ ( b ¯ × c ¯ ) λ B ( b ¯ × c ¯ ) ⋅ ( b ¯ × c ¯ ) b ¯

看过Multiview Geometry in Computer Vision书的同学一定知道那个 A−TA−1 A − T A − 1 描述了绝对二次曲线。（the image of
the absolute conic）
接下来的就跟张博士之前二维标定板标定文章的求解套路一样了，令 B=A−TA−1 B = A − T A − 1 构建线性方程组求解，有兴趣的直接看截图或者看原文，如果理解了张正友平面标定的求解过程，这儿你可以非常容易的想到如何求解。

奇异性 Singularities

文章最后还分析了这种1维标定的奇异性。我们需要观测6次，不是6次任意运动都可以用来求解的。共平面的5个点能确定一条绝对二次曲线，显然如果再在这条曲线上加一点，它并不能提供额外的约束，这就是此种方法的奇异性处。

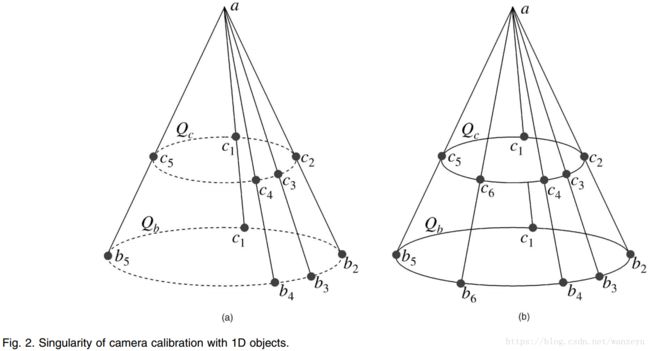
实验中固定一点再运动即可。

后记

十多年前的文章被我挖出来仔细学习（@-^-@）想认真学好机器视觉就从标定原理开始吧，对以后理解其中数学原理非常有帮助，缺了数学，那估计做出来的就是机器幻觉了。。。
惯例文章作者简介（竟然也是ZJU的）