数据分析07-数据清洗、矩阵、数学建模

数据分析-07

扩展：数据清洗

检测与处理重复值

pandas提供了一个名为drop_duplicates的去重方法。该方法只对DataFrame或者Series类型有效。这种方法不会改变数据原始排列，并且兼具代码简洁和运行稳定的特点。该方法不仅支持单一特征的数据去重，还能够依据DataFrame的其中一个或者几个特征进行去重操作。

dataFrame(Series).drop_duplicates(
    self, subset=None, keep='first', inplace=False)

参数名	说明
subset	接收string或sequence。表示进行去重的列。默认为None，表示全部列。
keep	接收特定string。表示重复时保留第几个数据。first：保留第一个。last：保留最后一个。false：只要有重复都不保留。默认为first。
inplace	接收boolean。表示是否在原表上进行操作。默认为False。

示例：

import pandas as pd
data=pd.DataFrame({'A':[1,1,2,2],'B':['a','b','a','b']})
data
data.drop_duplicates('A', 'first', inplace=True)
data

检测与处理缺失值

数据中的某个或某些特征的值是不完整的，这些值称为缺失值。
pandas提供了识别缺失值的方法isnull以及识别非缺失值的方法notnull，这两种方法在使用时返回的都是布尔值True和False。
结合sum函数和isnull、notnull函数，可以检测数据中缺失值的分布以及数据中一共含有多少缺失值。isnull和notnull之间结果正好相反，因此使用其中任意一个都可以判断出数据中缺失值的位置。

1）删除法

删除法分为删除观测记录和删除特征两种，pandas中提供了简便的删除缺失值的方法dropna，该方法既可以删除观测记录，亦可以删除特征。

pandas.DataFrame.dropna(
    self, axis=0, how='any', thresh=None, subset=None, inplace=False)

参数名	说明
axis	接收0或1。表示轴向，0为删除记录（行），1为删除特征（列）。默认为0。
how	接收特定string。表示删除的形式。any表示只要有缺失值存在就执行删除操作。all表示当且仅当全部为缺失值时执行删除操作。默认为any。
subset	接收类array数据。表示进行去重的列∕行。默认为None，表示所有列/行。
inplace	接收boolean。表示是否在原表上进行操作。默认为False。

示例：

dates = pd.date_range('20130101', periods=6)
df = pd.DataFrame(np.arange(24).reshape((6,4)),index=dates, columns=['A','B','C','D'])
df.iloc[0,1] = np.nan
df.iloc[1,2] = np.nan
# df1接收，判断是否有缺失数据 NaN, 为 True 表示缺失数据:
df1=df.isnull()
df1
#每一列的缺失数据
df2=df.isnull().sum()
df2
#整个表的缺失数据
df2.sum()
# df1接收，去掉有 NaN 的行, 可以使用 dropna 一旦出现NaN就去除整行
df3=df.dropna(axis=0,how='any')
df3

2）替换法

替换法是指用一个特定的值替换缺失值。
特征可分为离散型和连续型，两者出现缺失值时的处理方法也是不同的。
缺失值所在特征为连续型时，通常利用其均值、中位数和众数等描述其集中趋势的统计量来代替缺失值。缺失值所在特征为离散型时，则经常选择使用众数来替换缺失值。

插补方法	方法描述
均值/中位数/众数插补	根据属性值的类型用该属性取值的平均数/中位数/众数进行插补
使用固定值	将缺失的属性值用一个常量替换。
最近临插补	在记录中找到与缺失样本最接近的样本的该属性值插补
回归方法	对带有缺失值的变量,根据已有数据和与其有关的其他变量(因变量)的数据建立拟合模型来预测缺失的属性值
插值法	插值法是利用已知点建立合适的插值函数f(x),未知值由对应点x求出的函数值f(x)近似代替

pandas库中提供了缺失值替换的方法名为fillna，其基本语法如下：

pandas.DataFrame.fillna(
    value=None, method=None, axis=None, inplace=False, limit=None)

常用参数及其说明如下：

参数名	说明
value	接收scalar，dict，Series或者DataFrame。表示用来替换缺失值的值。无默认。
method	接收特定string。backfill或bfill表示使用下一个非缺失值填补缺失值。pad或ffill表示使用上一个非缺失值填补缺失值。默认为None。
axis	接收0或1。表示轴向。默认为1。
inplace	接收boolean。表示是否在原表上进行操作。默认为False。
limit	接收int。表示填补缺失值个数上限，超过则不进行填补。默认为None。

案例：

# df2接收，如果是将 NaN 的值用其他值代替, 比如代替成 0:
dates = pd.date_range('20130101', periods=6)
df = pd.DataFrame(np.arange(24).reshape((6,4)),index=dates, columns=['A','B','C','D'])
df.iloc[0,1] = np.nan
df.iloc[1,2] = np.nan
# 固定值填补
df2=df.fillna(value=0)
df2
# 相似值填补
df3=df.fillna(method='pad', axis=1)
df3

3）插值法
删除法简单易行，但是会引起数据结构变动，样本减少；替换法使用难度较低，但是会影响数据的标准差，导致信息量变动。在面对数据缺失问题时，除了这两种方法之外，还有一种常用的方法—插值法。

scipy提供了插值算法可以通过一组散点得到一个符合一定规律插值器函数。这样当我们给插值器函数更多未知x，插值函数将会返回相应的y用于填补缺失值。

需求：统计各小区彩民买彩票的情况：

彩民数量	彩票购买量
30	100注
40	120注
50	135注
60	155注
45	-
65	170注

scipy提供的插值方法如下：

import scipy.interpolate as si
func = si.interp1d(
    离散水平坐标, 
    离散垂直坐标,
    kind=插值算法(缺省为线性插值)
)

案例：

"""
demo07_inter.py  插值器
"""
import numpy as np
import matplotlib.pyplot as mp
import scipy.interpolate as si

x = [30, 40, 50, 60, 65]
y = [100, 120, 135, 155, 170]
mp.scatter(x, y)

xs = np.linspace(min(x), max(x), 200)
# 通过这些散点，构建一个线性插值函数
linear = si.interp1d(x, y, kind='cubic')
print(linear(45))
ys = linear(xs)
mp.plot(xs, ys)

mp.show()

检测与处理异常值

1. 简单统计量分析
   先对变量做一个描述性统计，找出哪些数据是不合理的，最常用的统计量是求最大值和最小值，判断变量是否在这个区间。

2. 3σ原则
   3σ原则又称为拉依达法则。该法则就是先假设一组检测数据只含有随机误差，对原始数据进行计算处理得到标准差，然后按一定的概率确定一个区间，认为误差超过这个区间的就属于异常值。
   这种判别处理方法仅适用于对正态或近似正态分布的样本数据进行处理。如果不符合正态分布，可以用远离平均值的多少倍标准差来表示。

3. 箱线图分析

   箱线图提供了识别异常值的一个标准，即异常值通常被定义为小于QL-1.5IQR或大于QU+1.5IQR的值。
   QL称为下四分位数，表示全部观察值中有四分之一的数据取值比它小。
   QU称为上四分位数，表示全部观察值中有四分之一的数据取值比它大。
   IQR称为四分位数间距，是上四分位数QU与下四分位数QL之差，其间包含了全部观察值的一半。

异常值的处理方法：

异常值处理方法	方法描述
删除含有异常值的记录	直接删除含有异常值的记录
视为缺失值	将异常值视为缺失值，按照缺失值方法处理。
平均值修正	用前后两个观测值的均值进行修正。
不处理	直接在含有异常值的数据集上进行数据建模。

矩阵

矩阵是numpy.matrix类型的对象，该类继承自numpy.ndarray，任何针对多维数组的操作，对矩阵同样有效，但是作为子类矩阵又结合其自身的特点，做了必要的扩充，比如：乘法计算、求逆等。

1. 矩阵对象的创建

# 等价于：numpy.matrix(..., copy=False)
# 由该函数创建的矩阵对象与参数中的源容器一定共享数据，无法拥有独立的数据拷贝
numpy.mat(任何可被解释为矩阵的二维容器)

# 该函数可以接受字符串形式的矩阵描述：
# 数据项通过空格分隔，数据行通过分号分隔。例如：'1 2 3; 4 5 6'
numpy.mat(拼块规则)

示例：创建matrix

# 创建matrix操作
import numpy as np

arr = np.arange(1, 10).reshape(3, 3)
print(arr)

# 第一种方式
m = np.matrix(arr, copy=True)
print(m)
print(m.shape)
print(type(m))

# 第二种方式:共享方式
m2 = np.mat(arr)
print(m2)

# 第三种方式
m3 = np.mat("1 2 3;4 5 6.0")
print(m3)

2. 矩阵的乘法运算

# 矩阵乘法
import numpy as np

arr = np.array([[1, 1, 1],
                [2, 2, 2],
                [3, 3, 3]])
# 数组相乘, 各对应位置元素相乘
print(arr * arr)

# 矩阵相乘，第n行乘m列之和，作为结果的n, m个元素
# 矩阵相乘，第一个矩阵列数必须等于第二个矩阵行数
m = np.mat(arr)
print(m * m)

3. 矩阵的逆矩阵

若两个矩阵A、B满足：AB = E （E为单位矩阵），则称B为A的逆矩阵。

单位矩阵

在矩阵的乘法中，有一种矩阵起着特殊的作用，如同数的乘法中的1，这种矩阵被称为单位矩阵。它是个方阵，从左上角到右下角的对角线（称为主对角线）上的元素均为1，除此以外全都为0，记为$I_n$或$E_n$ ，通常用I或E来表示。根据单位矩阵的特点，任何矩阵与单位矩阵相乘都等于本身，而且单位矩阵因此独特性有广泛用途。以下是一个单位矩阵示例：
$$E_3=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$
逆矩阵示例：

e = np.mat("1 2 6; 3 5 7; 4 8 9")
print(e.I)
print(e * e.I)

注意：在计算过程中，可能出现如下错误，说明该矩阵不可逆。

numpy.linalg.LinAlgError: Singular matrix

4. ndarray提供的矩阵API

ndarray提供了方法让多维数组替代矩阵的运算：

a = np.array([
    [1, 2, 6],
    [3, 5, 7],
    [4, 8, 9]])
# 点乘法求ndarray的点乘结果，与矩阵的乘法运算结果相同
k = a.dot(a)
print(k)
# linalg模块中的inv方法可以求取a的逆矩阵
l = np.linalg.inv(a)
print(l)

执行结果：

[[ 31  60  74]
 [ 46  87 116]
 [ 64 120 161]]
[[-0.73333333  2.         -1.06666667]
 [ 0.06666667 -1.          0.73333333]
 [ 0.26666667  0.         -0.06666667]]

5. 矩阵应用

案例：解线性方程组

假设一帮孩子和家长出去旅游，去程坐的是bus，小孩票价为3元，家长票价为3.2元，共花了118.4；回程坐的是Train，小孩票价为3.5元，家长票价为3.6元，共花了135.2。分别求小孩和家长的人数。使用矩阵求解。表达成方程为：
$$\begin{gathered} 3x+3.2y=118.4 \\ 3.5x+3.6y=135.2 \end{gathered}$$
表示成矩阵相乘：

$$\left[\begin{array}{cc}3& 3.2\\ 3.5& 3.6\end{array}\right]\times \left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}118.4\\ 135.2\end{array}\right]$$

import numpy as np

# 解方程
prices = np.mat('3 3.2; 3.5 3.6')
totals = np.mat('118.4; 135.2')

x = np.linalg.lstsq(prices, totals)[0]  # 求最小二乘解
print(x)

x = np.linalg.solve(prices, totals)  # 求解线性方程的解
print(x)

x = prices.I * totals  # 利用矩阵的逆进行求解
print(x)

案例：斐波那契数列

1 1 2 3 5 8 13 21 34 …

X      1   1    1   1    1   1
       1   0    1   0    1   0
    --------------------------------
1  1   2   1    3   2    5   3
1  0   1   1    2   1    3   2
 F^1    F^2      F^3 	  F^4  ...  f^n

代码

import numpy as np
n = 35

# 使用递归实现斐波那契数列
def fibo(n):
    return 1 if n < 3 else fibo(n - 1) + fibo(n - 2)
print(fibo(n))

# 使用矩阵实现斐波那契数列
print(int((np.mat('1. 1.; 1. 0.') ** (n - 1))[0, 0]))

数学建模

1. 线性模型

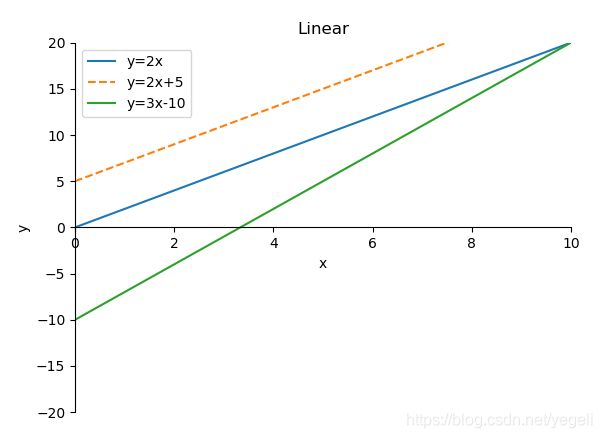
如下直线方程属于线性方程：
$$y=kx+b$$
图像可表示为：

在实际应用，输入和输出可以用线性模型进行拟合，称之为线性模型或线性问题（如房屋面积与总价、成年人的身高与体重）。表示成图像如下图所示：

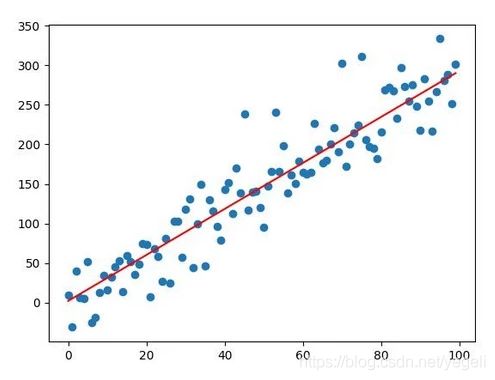
线性拟合

线性拟合就是试图找到一个最优的线性方程，可以最好的匹配当前样本（到所有样本的距离之和最短，误差最小）。若已知样本只有一个自变量$x$与一个因变量$y$，则线性方程可表示为：
$$y=kx+b$$
线性拟合就是根据一组x, y的值，来寻求最佳k,b的值，这个过程也可称为线性回归。

有一组散点描述时间序列下的股价：

[x1, y1]
[x2, y2]
[x3, y3] 
...
[xn, yn]

我们希望所有点都可以被线性方程$y=kx+b$表示，姑且把所有样本带入方程可得：

kx1 + b = y1
kx2 + b = y2
kx3 + b = y3
...
kxn + b = yn

这一组方程表示为矩阵相乘格式：

$$\left[\begin{array}{cc}x{}_1& 1\\ x{}_2& 1\\ x{}_3& 1\\ x{}_n& 1\end{array}\right]\times \left[\begin{array}{c}k\\ b\end{array}\right]=\left[\begin{array}{c}y{}_1\\ y{}_2\\ y{}_3\\ y{}_n\end{array}\right]$$

样本过多，每两组方程即可求得一组k与b的值。$ A B x np.linalg.lstsq(A, B) $可以通过最小二乘法求出所有结果中拟合误差最小的k与b的值。

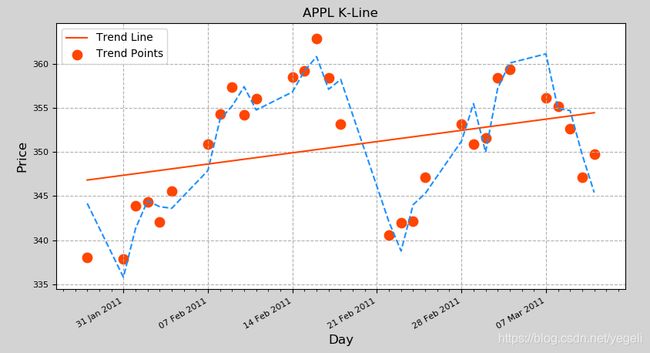
案例：利用线型拟合画出股价的趋势线

1. 绘制趋势线（趋势可以表示为最高价、最低价、收盘价的均值）：

# 线性拟合示例
import numpy as np
import datetime as dt


#### 1.读取数据
# 日期格式转换函数: 将日月年转换为年月日格式
def dmy2ymd(dmy):
    dmy = str(dmy, encoding="utf-8")
    # 从指定字符串返回一个日期时间对象
    dat = dt.datetime.strptime(dmy, "%d-%m-%Y").date()  # 字符串转日期
    tm = dat.strftime("%Y-%m-%d")  # 日期转字符串
    return tm


dates, open_prices, highest_prices, lowest_prices, close_prices = \
    np.loadtxt("../da_data/appl.csv",  # 文件路径
               delimiter=",",  # 指定分隔符
               usecols=(1, 3, 4, 5, 6),  # 读取的列(下标从0开始)
               unpack=True,  # 拆分数据
               dtype="M8[D], f8, f8, f8, f8",  # 指定每一列的类型
               converters={1: dmy2ymd})  #

#### 2.绘制图像
import matplotlib.pyplot as mp
import matplotlib.dates as md

# 绘制k线图，x轴为日期
mp.figure("APPL K-Line", facecolor="lightgray")
mp.title("APPL K-Line")
mp.xlabel("Day", fontsize=12)
mp.ylabel("Price", fontsize=12)

# 获取坐标轴
ax = mp.gca()
# 设置主刻度定位器为周定位器(每周一显示刻度文本)
ax.xaxis.set_major_locator(md.WeekdayLocator(byweekday=md.MO))
ax.xaxis.set_major_formatter(md.DateFormatter("%d %b %Y"))  # %b表示月份简写
# 设置次刻度定位器为天定位器
ax.xaxis.set_minor_locator(md.DayLocator())
mp.tick_params(labelsize=8)
dates = dates.astype(md.datetime.datetime)

mp.plot(dates, open_prices, color="dodgerblue", linestyle="--")
mp.gcf().autofmt_xdate()  # 旋转、共享日期显示

# 求得每天的趋势价格: 最高价、最低价、收盘价求平均值作为趋势价
trend_prices = (highest_prices + lowest_prices + close_prices) / 3
mp.scatter(dates, trend_prices, marker="o",
           color="orangered", s=80, label="Trend Points")

# 绘制趋势线
# A：日期转换为数字
# Y: 趋势价格(trend_prices)
days = dates.astype("M8[D]").astype("int32")
# print(days)
# column_stack: 将1d数组堆叠成2d数组
# ones_like: 返回与给定数组具有相同形状和类型的数组
A = np.column_stack((days, np.ones_like(days)))

# lstsq(least-squares solution):最小二乘法，最小化误差的平方和寻找数据的最佳函数匹配
Y = trend_prices
x = np.linalg.lstsq(A, Y, rcond=None)[0]  # x中包含了k, b的值

trend_line = x[0] * days + x[1]  # y = kx + b
mp.plot(dates, trend_line, color="orangered", label="Trend Line")

if x[0] > 0:
    print("总体趋势上涨")
elif x[0] < 0:
    print("总体趋势下跌")
else:
    print("总体趋势持平")

mp.grid(linestyle="--")
mp.legend()
mp.show()

执行结果：

控制台输出：

总体趋势上涨

课后作业

• 绘制顶部压力线（趋势线+(最高价 - 最低价)）

trend_points = (highest_prices + lowest_prices + closing_prices) / 3
spreads = highest_prices - lowest_prices
resistance_points = trend_points + spreads
days = dates.astype(int)
x = np.linalg.lstsq(a, resistance_points)[0]
resistance_line = days * x[0] + x[1]
mp.scatter(dates, resistance_points, c='orangered', alpha=0.5, s=60, zorder=2)
mp.plot(dates, resistance_line, c='orangered', linewidth=3, label='Resistance')

• 绘制底部支撑线（趋势线-(最高价 - 最低价)）

trend_points = (highest_prices + lowest_prices + closing_prices) / 3
spreads = highest_prices - lowest_prices
support_points = trend_points - spreads
days = dates.astype(int)
x = np.linalg.lstsq(a, support_points)[0]
support_line = days * x[0] + x[1]
mp.scatter(dates, support_points, c='limegreen', alpha=0.5, s=60, zorder=2)
mp.plot(dates, support_line, c='limegreen', linewidth=3, label='Support')

线性模型的应用场景

海底管道腐蚀速率 数学模型

x1			x2			x3			y
深度		某元素浓度		温度		腐蚀速率
100		   0.001		 2			0.0001
100		   0.001		 2			0.0001
100		   0.001		 2			0.0001
100		   0.001		 2			0.0001
100		   0.001		 2			0.0001

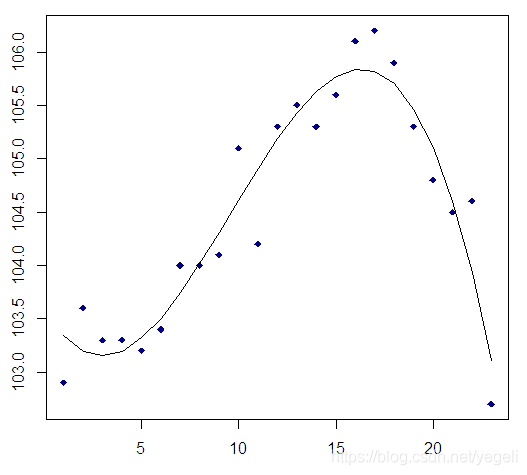
2. 多项式模型

在有些数据分布中，使用一条曲线比直线能更好拟合数据，这就需要用到多项式拟合。如下图所示分布：

多项式的一般形式：
$$y=p_0{x}^n+p_1{x}^{n-1}+p_2{x}^{n-2}+p_3{x}^{n-3}+...+p_n$$
多项式拟合的目的是为了找到一组 $p_0,p_1,...,p_n$，使得拟合方程尽可能的与实际样本数据相符合。

假设拟合得到的多项式如下：
$$f(x)=p_0{x}^n+p_1{x}^{n-1}+p_2{x}^{n-2}+p_3{x}^{n-3}+...+p_n$$
则拟合函数与真实结果的差方如下：
$$loss=(y_1-f(x_1){)}^2+(y_2-f(x_2){)}^2+...+(y_n-f(x_n){)}^2$$
那么多项式拟合的过程即为求取一组$p_0,p_1,...,p_n$, 使得loss的值最小。在程序中，多项式可以表示为一个数组，格式如下：

f = [-6, 3, 8, 1]

表示多项式为：
$$y=-6x^3+3x^2+8x+1$$
多项式拟合相关API：

X = [x1, x2, ..., xn]
Y = [y1, y2, ..., yn]
#根据一组样本，并给出最高次幂，求出拟合系数
np.polyfit(X, Y, 最高次幂)

多项式运算相关API：

#根据拟合系数与自变量求出拟合值, 由此可得拟合曲线坐标样本数据 [X, Y']
np.polyval(P, X)->Y'

#多项式函数求导，根据拟合系数求出多项式函数导函数的系数
np.polyder(P)->Q 

#已知多项式系数Q 求多项式函数的根（与x轴交点的横坐标）
xs = np.roots(Q)

#两个多项式函数的差函数（对应系数相减）的系数（可以通过差函数的根求取两个曲线的交点）
Q = np.polysub(P1, P2)

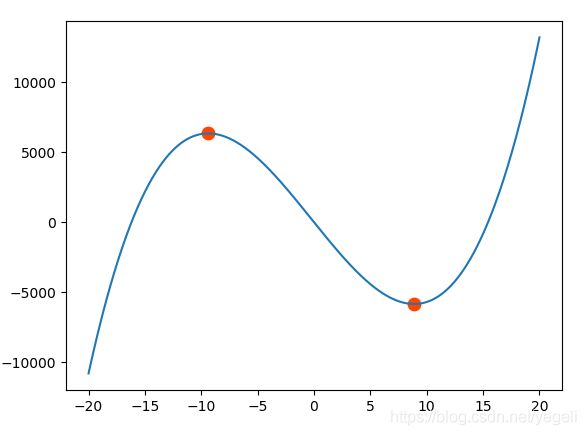
案例：求多项式 y = 4x³ + 3x² - 1000x + 1曲线驻点的坐标。

'''
1. 求出多项式的导函数
2. 求出导函数的根，若导函数的根为实数，则该点则为曲线驻点。
'''
import numpy as np
import matplotlib.pyplot as mp

x = np.linspace(-20, 20, 1000) #生成数据
P = [4, 3, -1000, 1] #原函数的系数列表
y = np.polyval(P, x) #计算函数的值

Q = np.polyder([4, 3, -1000, 1])  # 求导函数系数
print(Q)
xs = np.roots(Q)  # 求导函数的根（y等于0，此时函数变化率为0，即切线为水平线）
ys = np.polyval(P, xs) #计算变化率为0时的y值

mp.plot(x, y)
mp.scatter(xs, ys, s=80, c="orangered")
mp.show()

执行结果：

案例：使用多项式函数拟合两只股票bhp、vale的差价函数：

'''
1. 计算两只股票的差价
2. 利用多项式拟合求出与两只股票差价相近的多项式系数，最高次为4
'''
import numpy as np
import datetime as dt

#### 1.读取数据
# 日期格式转换函数: 将日月年转换为年月日格式
def dmy2ymd(dmy):
    dmy = str(dmy, encoding="utf-8")
    # 从指定字符串返回一个日期时间对象
    dat = dt.datetime.strptime(dmy, "%d-%m-%Y").date()  # 字符串转日期
    tm = dat.strftime("%Y-%m-%d")  # 日期转字符串
    return tm


dates, bhp_close_prices = np.loadtxt("../da_data/bhp.csv",  # 文件路径
                                     delimiter=",",  # 指定分隔符
                                     usecols=(1, 6),  # 读取的列(下标从0开始)
                                     unpack=True,  # 拆分数据
                                     dtype="M8[D], f8",  # 指定每一列的类型
                                     converters={1: dmy2ymd})  #
dates, vale_close_prices = np.loadtxt("../da_data/vale.csv",  # 文件路径
                                      delimiter=",",  # 指定分隔符
                                      usecols=(1, 6),  # 读取的列(下标从0开始)
                                      unpack=True,  # 拆分数据
                                      dtype="M8[D], f8",  # 指定每一列的类型
                                      converters={1: dmy2ymd})  #

#### 2.绘制图像
import matplotlib.pyplot as mp
import matplotlib.dates as md

# 绘制k线图，x轴为日期
mp.figure("Polyfit", facecolor="lightgray")
mp.title("Polyfit")
mp.xlabel("Date", fontsize=12)
mp.ylabel("Price", fontsize=12)

# 获取坐标轴
ax = mp.gca()
# 设置主刻度定位器为周定位器(每周一显示刻度文本)
ax.xaxis.set_major_locator(md.WeekdayLocator(byweekday=md.MO))
ax.xaxis.set_major_formatter(md.DateFormatter("%d %b %Y"))  # %b表示月份简写
# 设置次刻度定位器为天定位器
ax.xaxis.set_minor_locator(md.DayLocator())
mp.tick_params(labelsize=8)
dates = dates.astype(md.datetime.datetime)

# 绘制差价函数
diff_prices = bhp_close_prices - vale_close_prices
mp.plot(dates, diff_prices, label="diff")

# 寻找拟合差价函数
days = dates.astype("M8[D]").astype("int32")
# 做最小二乘多项式拟合
P = np.polyfit(days,  # x
               diff_prices,  # y
               4)  # 维度
poly_prices = np.polyval(P, days) # 根据求得的系数，重新计算函数值
mp.plot(dates, poly_prices, label="Polyfit line")
mp.gcf().autofmt_xdate()  # 旋转、共享日期显示

mp.grid(linestyle="--")
mp.legend()
mp.show()

执行结果：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xy6pjJQy-1593500363955)(C:/Users/xuming/Desktop/code/images/%E8%82%A1%E7%A5%A8%E5%B7%AE%E5%87%BD%E6%95%B0%E5%A4%9A%E9%A1%B9%E5%BC%8F%E6%8B%9F%E5%90%88.png)]

多项式拟合的注意事项：

• 多项式拟合不能在数据样本之外的范围做预测
• 多项式拟合时容易造成过拟合（函数和样本拟合度太高，样本以外的数据则拟合度很低）

3. 基于函数矢量化的股票回测模型

函数的矢量化指通过一个只能处理标量数据的函数得到一个可以处理矢量数据的函数，从而可以对大量数据进行矢量化计算。

numpy提供了vectorize函数，可以把处理标量的函数矢量化，返回的函数可以直接处理ndarray数组。

# vectorize函数矢量化示例
import math
import numpy as np


def func(x, y):
    return math.sqrt(x ** 2 + y ** 2)


# 标量计算
x, y = 3, 4	
print(func(x, y))

# 矢量化计算
X = np.array([3, 6, 9])
Y = np.array([4, 8, 12])

vect_func = np.vectorize(func)  # 创建函数矢量化对象

print(vect_func(X, Y))

执行结果：

5.0
[ 5. 10. 15.]

numpy还提供了frompyfuc函数，也可以完成与vectorize相同的功能：

# 把foo转换成矢量函数
# 原型：frompyfunc(func, nin, nout)
# func: 要矢量化的函数
# nin:输入参数个数
# nout:返回值个数
fun = np.frompyfunc(foo, 2, 1)
fun(X, Y)

案例：定义一种投资策略，传入某日期，基于均线理论返回是否应该按收盘价购买，并通过历史数据判断这种策略是否值得实施。

import numpy as np
import matplotlib.pyplot as mp
import datetime as dt
import matplotlib.dates as md

# 日期格式转换函数: 将日月年转换为年月日格式
def dmy2ymd(dmy):
    dmy = str(dmy, encoding="utf-8")
    # 从指定字符串返回一个日期时间对象
    dat = dt.datetime.strptime(dmy, "%Y/%m/%d").date()
    tm = dat.strftime("%Y-%m-%d")  # 格式化
    return tm

dates, opening_prices, highest_prices, lowest_prices, closing_prices, ma5, ma10= \
    np.loadtxt("../data/pfyh.csv", #文件路径
               delimiter=",", #指定分隔符
               usecols=(0,1,2,3,4,5,6), #读取的列(下标从0开始)
               unpack=True, #拆分数据
               dtype="M8[D], f8, f8, f8, f8, f8, f8") #
mp.plot(dates, closing_prices)
mp.show()
# 定义一种投资策略，传入日期，基于均线理论返回是否应该按收盘价购买 1:应买入  0:应持有现状  -1:应卖出
def profit(m8date):
    mma5 = ma5[dates < m8date]
    mma10 = ma10[dates < m8date]
    # 至少两天数据才可以进行预测
    if mma5.size < 2:
        return 0
    # 出现金叉，则建议买入
    if (mma5[-2] <= mma10[-2]) and (mma5[-1] >= mma10[-1]):
        return 1
    # 出现死叉，则建议卖出
    if (mma5[-2] >= mma10[-2]) and (mma5[-1] <= mma10[-1]):
        return -1
    return 0

# 矢量化投资函数
vec_func = np.vectorize(profit)
# 使用适量换函数计算收益
profits = vec_func(dates)
print(profits)

# 定义资产
assets = 1000000
stocks = 0
payment_price = 0
status = 0
for index, profit in enumerate(profits):
    current_price = closing_prices[index]
    # 如果是买入并且赔了的状态，若已经跌出5%，则强制卖出
    if status == 1:
        payment_assets = payment_price * stocks
        current_assets = current_price * stocks
        if (payment_assets > current_assets) and ((payment_assets-current_assets) > payment_assets *0.05):
            payment_price = current_price
            assets = assets + stocks * payment_price
            stocks = 0
            status = -1
            print('止损：dates:{}, curr price:{:.2f}, assets:{:.2f}, stocks:{:d}'.format(dates[index], current_price, assets, stocks))
    if (profit == 1) and (status != 1): # 买入
        payment_price = current_price
        stocks = int(assets / payment_price)
        assets = assets - stocks * payment_price
        status = 1
        print('买入：dates:{}, curr price:{:.2f}, assets:{:.2f}, stocks:{:d}'.format(dates[index], current_price, assets, stocks))
    if (profit == -1) and (status != -1): # 卖出
        payment_price = current_price
        assets = assets + stocks * payment_price
        stocks = 0
        status = -1
        print('卖出：dates:{}, curr price:{:.2f}, assets:{:.2f}, stocks:{:d}'.format(dates[index], current_price, assets, stocks))
    print('持有：dates:{}, curr price:{:.2f}, assets:{:.2f}, stocks:{:d}'.format(dates[index], current_price, assets, stocks))

代码总结

数据清洗

import numpy as np
import pandas as pd

检测与处理重复值

df = pd.DataFrame({'Name':['zs', 'zs', 'ls'], 'score':[20, 20, 15]})
df

	Name	score
0	zs	20
1	zs	20
2	ls	15

df.drop_duplicates(keep='last')

	Name	score
1	zs	20
2	ls	15

检测与处理缺失值

ratings = pd.read_json('../../data/ratings.json')
ratings

	John Carson	Michelle Peterson	William Reynolds	Jillian Hobart	Melissa Jones	Alex Roberts	Michael Henry
Inception	2.5	3.0	2.5	NaN	3	3.0	NaN
Pulp Fiction	3.5	3.5	3.0	3.5	4	4.0	4.5
Anger Management	3.0	1.5	NaN	3.0	2	NaN	NaN
Fracture	3.5	5.0	3.5	4.0	3	5.0	4.0
Serendipity	2.5	3.5	NaN	2.5	2	3.5	1.0
Jerry Maguire	3.0	3.0	4.0	4.5	3	3.0	NaN

# 检测缺失值
ratings.isnull()

	John Carson	Michelle Peterson	William Reynolds	Jillian Hobart	Melissa Jones	Alex Roberts	Michael Henry
Inception	False	False	False	True	False	False	True
Pulp Fiction	False	False	False	False	False	False	False
Anger Management	False	False	True	False	False	True	True
Fracture	False	False	False	False	False	False	False
Serendipity	False	False	True	False	False	False	False
Jerry Maguire	False	False	False	False	False	False	True

# 删除缺失值
ratings.dropna(axis=1)

	John Carson	Michelle Peterson	Melissa Jones
Inception	2.5	3.0	3
Pulp Fiction	3.5	3.5	4
Anger Management	3.0	1.5	2
Fracture	3.5	5.0	3
Serendipity	2.5	3.5	2
Jerry Maguire	3.0	3.0	3

ratings.fillna(999)

	John Carson	Michelle Peterson	William Reynolds	Jillian Hobart	Melissa Jones	Alex Roberts	Michael Henry
Inception	2.5	3.0	2.5	999.0	3	3.0	999.0
Pulp Fiction	3.5	3.5	3.0	3.5	4	4.0	4.5
Anger Management	3.0	1.5	999.0	3.0	2	999.0	999.0
Fracture	3.5	5.0	3.5	4.0	3	5.0	4.0
Serendipity	2.5	3.5	999.0	2.5	2	3.5	1.0
Jerry Maguire	3.0	3.0	4.0	4.5	3	3.0	999.0

ratings.fillna(method='ffill')

	John Carson	Michelle Peterson	William Reynolds	Jillian Hobart	Melissa Jones	Alex Roberts	Michael Henry
Inception	2.5	3.0	2.5	NaN	3	3.0	NaN
Pulp Fiction	3.5	3.5	3.0	3.5	4	4.0	4.5
Anger Management	3.0	1.5	3.0	3.0	2	4.0	4.5
Fracture	3.5	5.0	3.5	4.0	3	5.0	4.0
Serendipity	2.5	3.5	3.5	2.5	2	3.5	1.0
Jerry Maguire	3.0	3.0	4.0	4.5	3	3.0	1.0

插值法

x = [30, 40, 50, 60, 65]
y = [100, 120, 135, 155, 170]
import scipy.interpolate as si
func = si.interp1d(x, y)
func(49)

矩阵

import numpy as np

# 创建矩阵对象
data = np.arange(9).reshape(3, 3)
m = np.mat(data)
print(m, type(m))

[[0 1 2]
 [3 4 5]
 [6 7 8]] 

m = np.mat('1 2 3; 4 5 6')
print(m, type(m))

[[1 2 3]
 [4 5 6]] 

矩阵乘法

data = np.arange(9).reshape(3, 3)
# ndarray的乘法
print(data * data)
# 矩阵乘法
print('-' * 40)
m = np.mat(data)
print(m * m)

[[ 0  1  4]
 [ 9 16 25]
 [36 49 64]]
----------------------------------------
[[ 15  18  21]
 [ 42  54  66]
 [ 69  90 111]]

逆矩阵

e = np.mat('1 3 6; 2 5 6; 4 8 11')
print(e)
print(e.I)
print(e * e.I)

[[ 1  3  6]
 [ 2  5  6]
 [ 4  8 11]]
[[-0.63636364 -1.36363636  1.09090909]
 [-0.18181818  1.18181818 -0.54545455]
 [ 0.36363636 -0.36363636  0.09090909]]
[[ 1.00000000e+00 -2.22044605e-16  5.55111512e-17]
 [ 2.22044605e-16  1.00000000e+00  5.55111512e-17]
 [ 1.11022302e-16 -1.11022302e-16  1.00000000e+00]]

解方程组

A = np.mat('3 3.2; 3.5 3.6')
B = np.mat('118.4; 135.2')
x = A.I * B
x

matrix([[16.],
        [22.]])

斐波那契数列

def feb(n):
    if n<3:
        return 1
    return feb(n-1) + feb(n-2)

n = 37
feb(n)

24157817

F = np.mat('1 1; 1 0')
F**40

matrix([[165580141, 102334155],
        [102334155,  63245986]])

数学建模

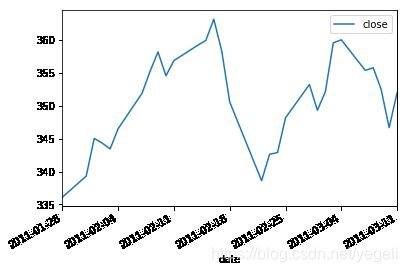
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

data = pd.read_csv('../data/aapl.csv', header=None, usecols=[1, 6])
data.columns = ['date', 'close']
# 把date字段，转成日期类型
def todate(item):
    datestr = '-'.join(item.split('-')[::-1])
    return pd.to_datetime(datestr)
data['date'] = data['date'].apply(todate)

data.plot(x='date', y='close')

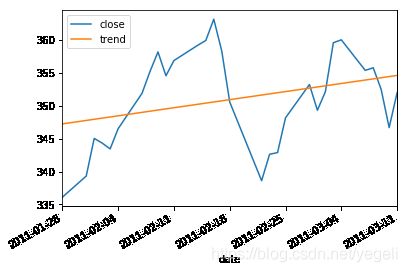
# 吧日期变成相应的数字
days = (data['date'] - pd.to_datetime('2011-01-01')).dt.days
# 整理A与B， 调用linalg.lstsq方法求拟合
A = pd.DataFrame({'x': days, '1': np.ones_like(days)})
B = data['close']
x = np.linalg.lstsq(A, B)[0]
# x中即包含了趋势线的斜率与截距
# 若希望在图像中绘制趋势线，需要求得每天的趋势价格，绘制图像即可。
data['trend'] = x[0] * days + x[1]
data.plot(x='date', y=['close', 'trend'])

C:\Users\xuming\AppData\Local\Continuum\anaconda3\envs\aid\lib\site-packages\ipykernel_launcher.py:6: FutureWarning: `rcond` parameter will change to the default of machine precision times ``max(M, N)`` where M and N are the input matrix dimensions.
To use the future default and silence this warning we advise to pass `rcond=None`, to keep using the old, explicitly pass `rcond=-1`.

​

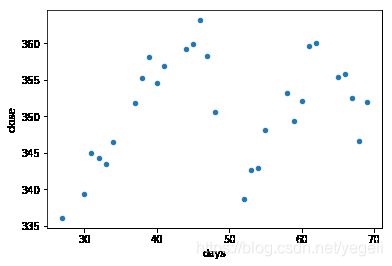
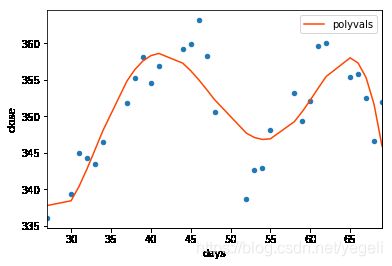
多项式模型

data['days'] = days
# 绘图days ~ close
data.plot.scatter(x='days', y='close')

p = np.polyfit(data['days'], data['close'], 5)
p

array([-1.97919911e-05,  4.66447608e-03, -4.27249275e-01,  1.89446747e+01,
       -4.05027302e+02,  3.67749979e+03])

# 把 days带入拟合得到的多项式，求得拟合结果
polyvals = np.polyval(p, days)
data['polyvals'] = polyvals
ax = data.plot.scatter(x='days', y='close')
data.plot(x='days', y='polyvals', ax=ax, color='orangered')

# 计算波峰与波谷的位置
# 针对多项式函数求导：
q = np.polyder(p)
# 求导函数的根
xs = np.roots(q)
xs
# 当x=60时，是涨中还是跌中？
np.polyval(q, 60)

1.6278084547757885