范数理论及其应用
在提到范数这一概念的时候,我想说说范数出现的原因,特别是大数据热的飞起的今天。首先我们引出如下定理:
由上定理可知,我们需要对序列中的每个元素都检查其是否收敛与某个数,该问题属于遍历性问题。对于
遍历性问题而言,数量小的还好办,数据量大的话计算机就无能为力了。所以我们希望将遍历性问题转化为非
遍历性问题。还是拿上面定理举例。
这就引出了范数的概念,我理解的范数就是表示数与数之间的距离的函数。
1.向量范数
定义:
对于所有满足上述条件的实值函数都可以称为向量范数,可以证明这样的向量范数不唯一,
所以就有了1范数、2范数、无穷范数的概念,正是由于其不唯一性,我们在工程实践中可以
针对不同问题选择合适的向量范数,简化运算。
范数的几何表示:
这样理解范数这个概念应该好理解一点。
对于向量范数,具有如下性质:
2矩阵范数
矩阵范数比向量范数的区别就是多了第四条公理,其他都一样。既然出现了两种范数,
我们就希望知道矩阵范数与向量范数之间存在什么关系??就引出了矩阵范数和向量范数
相容的概念。
由第二条定理可以知道,一个矩阵范数可以通过向量范数来表示,我觉着这条性质是矩阵范数
与向量范数本质上的关系。通过第二条定理我们可以推出如下三条定理,这三条定理给我们阐述了
怎么求矩阵的1范数、2范数和无穷范数。
3 范数的一些应用
学了范数,我想更多的关注点应该在于范数有哪些用处??这里我只讲三点用处。
3.1.矩阵的非奇异条件
我们知道,在很多时候会遇到判断矩阵是否可逆??目前我们知道的判断矩阵是否可逆的
办法就是判断矩阵的秩是否为0,或者矩阵是否满秩。现在利用范数又有了一种方法:
该定理可以干什么??这个定理不但可以判断矩阵是否可逆,还可以判断矩阵的放大量。
我们知道对于一个观测系统其观测方程可以写成:y=bx,其中y为测量变量,x为观测变量。而
对于一个系统中我们常常得到的是测量变量y,怎么通过测量变量来得到观测变量x,则有
就拿1/x这个式子来说,当x趋向于0时,x稍微改变一点,1/x这个式子的结果是不是会放大的很大。而我们在
测量过程中,或者说在建模当中肯定会出现误差,这时候如果矩阵的秩接近0,求逆就会存在很大的误差,这
就是矩阵的病态。通过范数我们就可以估计逆矩阵的值。
3.2.近似矩阵
上面我们说了,对于矩阵求逆会出现病态,我们就想知道如果测量矩阵b出现误差为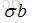 ,估计矩
,估计矩
阵的 逆相应会发生多大的误差??
我想解读一下这三条性质以及这三条性质能干嘛??首先这条定理成立是有条件的,
在用这条定理的时候一定要注意,条件1矩阵A一定要可逆的,条件2是矩阵A和误差矩阵相
乘的范数小于1(表明误差满足一定条件)。对于性质1,一个矩阵A加上一个误差矩阵后,
我们想知道该矩阵是否可逆, 如果不可逆的话,所有的估计都是白费功夫,所以该性质表明
一个可逆矩阵A在误差满足一定 条件的时候是可逆 的,解决了我们的疑虑。对于性质2,性质2
解决了我们想知道对于一个矩阵存在误差后,矩阵逆的误差放大量有多少??对于性质3,解
决了误差的相对放大量的上界是多少,注意这里是相对放大量??所以说这三条定理基本解决
了工程上对于误差要解决的问题:1.带误差的矩阵逆是否存在?2.存在的误差情况下,求逆后的
误差放大量是多少??相对原矩阵的相对放大量是多少??
3.3谱半径
不知道你们学过现代控制理论没有??对于一个系统的可观,可控有没有一定的了解。在
现代控制理论中,对于状态矩阵,如果状态矩阵的特征值都小于1,则该系统可控。但是在工程
中求取特征值和矩阵求逆一样,非常困难,所以我们就想我们不一定非得把特征值都求出来呀,
如果我们知道最大特征值,然后最大特征值和1比较不就知道该系统是否可控了嘛。这就引出了
谱半径的概念:
既然有了谱半径的概念,那么我们怎么估计谱半径的大小呢??这时候就需要范数出场了。
这时候的你需要看看怎么求1范数、2范数、无穷范数的方法??对于1范数、无穷范数的方法
真的是简单的不能再简单了,为啥还要傻傻的去求矩阵的特征值呢??
待续









