pytorch实现分类问题（五）

文章链接

刘二大人

别人的博客，写的不错

Pytorch详解NLLLoss和CrossEntropyLoss

pytorch二分类

import numpy as np
import torch
import matplotlib.pyplot as plt

# 加载csv文件数据
xy = np.loadtxt(r'D:\学习资料\pytorch刘二大人课件\PyTorch深度学习实践\diabetes.csv.gz', delimiter=',', dtype=np.float32)
x_data = torch.from_numpy(xy[:, :-1])  # 第一个‘：’是指读取所有行，第二个‘：’是指从第一列开始，最后一列不要
y_data = torch.from_numpy(xy[:, [-1]])  # [-1] 最后得到的是个矩阵，返回二维数据类型，若 只是 -1 表示一维数据


# x_data.shape为[756,8]
# y_data.shape为[756,1]

# 定义model类,继承Module
class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear1 = torch.nn.Linear(8, 6)  # 输入数据x的特征是8维，x有8个特征
        self.linear2 = torch.nn.Linear(6, 4)
        self.linear3 = torch.nn.Linear(4, 1)
        self.sigmoid = torch.nn.Sigmoid()  # 将其看作是网络的一层，而不是简单的函数使用

    def forward(self, x):
        # 添加非线性激活函数
        x = self.sigmoid(self.linear1(x))
        x = self.sigmoid(self.linear2(x))
        x = self.sigmoid(self.linear3(x))
        return x


model = Model()

# 创建二分类的交叉熵损失
criterion = torch.nn.BCELoss(reduction='mean')
# 创建优化器，梯度下降，参数为model中所有的参数，学习率为0.1
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)

epoch_list = []
loss_list = []
# 训练过程：前馈 forward, 反馈backward, 更行update
for epoch in range(100):
    # 自动调用forward函数，进行前馈
    y_pred = model(x_data)
    # 计算损失值
    loss = criterion(y_pred, y_data)
    print(epoch, loss.item())
    epoch_list.append(epoch)
    loss_list.append(loss.item())

    # 优化器梯度清空
    optimizer.zero_grad()
    # 损失回馈，tenser会记录所有组成它的变量，就通过记录的值进行反馈(反向传播)
    loss.backward()
    # 跟新优化
    optimizer.step()

plt.plot(epoch_list, loss_list)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()

""" 
第一层的参数：
权重：
layer1_weight = model.linear1.weight.data
偏置量：
layer1_bias = model.linear1.bias.data
"""

dataloader块化数据读取

import torch
import numpy as np
from torch.utils.data import Dataset
from torch.utils.data import DataLoader


# 实现dataset进行数据读取
class DiabetesDataset(Dataset):
    def __init__(self, filepath):
        xy = np.loadtxt(filepath, delimiter=',', dtype=np.float32)
        self.len = xy.shape[0]  # shape(多少行，多少列)
        self.x_data = torch.from_numpy(xy[:, :-1])
        self.y_data = torch.from_numpy(xy[:, [-1]])

    def __getitem__(self, index):
        return self.x_data[index], self.y_data[index]

    def __len__(self):
        return self.len


# 这种方式主要是我们要使用所有数据计算梯度下降一次太费时间了，所以采用minbatch方式进行梯度下降
dataset = DiabetesDataset(r'D:\学习资料\pytorch刘二大人课件\PyTorch深度学习实践\diabetes.csv.gz')
# dataloader进行数据块化读取，会生成一个列表，列表中每个元素就是一个块，每个块中包含dataset.__getitem__()返回的值，就是第一项为x，第二项为y
train_loader = DataLoader(dataset=dataset,  # 实现的对象
                          batch_size=32,  # 每一块数据就是batch_size个，最后数据不足batch_size就用最后的自己组成一个块
                          shuffle=True,  # 随机化打乱
                          num_workers=2)  # num_workers 多线程


# 创建model对象
class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear1 = torch.nn.Linear(8, 6)
        self.linear2 = torch.nn.Linear(6, 4)
        self.linear3 = torch.nn.Linear(4, 1)
        self.sigmoid = torch.nn.Sigmoid()  # sigmoid作为激活函数

    def forward(self, x):
        # 前馈构建计算图
        x = self.sigmoid(self.linear1(x))
        x = self.sigmoid(self.linear2(x))
        x = self.sigmoid(self.linear3(x))
        return x


model = Model()

# 创建损失函数和优化方法
criterion = torch.nn.BCELoss(reduction='mean')
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

# 前馈（构架计算图），反向传播，优化更新
if __name__ == '__main__':
    # 对所有数据进行优化100次
    for epoch in range(100):
        # 每轮数据对dataloader进行数据块化梯度下降
        for i, data in enumerate(train_loader, 0):  # train_loader 是先shuffle后mini_batch
            # data[0]就是数据集，data[1]就是label标签
            inputs, labels = data
            # 实例化模型，间接调用forward函数返回预测值，返回值并不是forward方法返回的值
            y_pred = model(inputs)
            # 构建计算图，计算损失
            loss = criterion(y_pred, labels)

            # print(epoch, i, loss.item())

            # 优化器参数清零
            optimizer.zero_grad()
            # 反向传播
            loss.backward()
            # 更新
            optimizer.step()

MNIST多分类

数据集下载

import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
from torch import optim

# bath——size数据准备
batch_size = 64

transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])  # 归一化,均值和方差
# 加载train数据集
train_dataset = datasets.MNIST(root=r'D:\code_management\pythonProject/dataset/mnist/', train=True, download=False,
                               transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
# 加载test数据集
test_dataset = datasets.MNIST(root=r'D:\code_management\pythonProject/dataset/mnist/', train=False, download=False,
                              transform=transform)
test_loader = DataLoader(test_dataset, shuffle=True, batch_size=batch_size)


class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        # 数据集大小为28*28的，展平就是784
        self.l1 = torch.nn.Linear(784, 512)
        self.l2 = torch.nn.Linear(512, 256)
        self.l3 = torch.nn.Linear(256, 128)
        self.l4 = torch.nn.Linear(128, 64)
        self.l5 = torch.nn.Linear(64, 10)  # 最后一层到10维，因为手写数据集0~9有10类数据

    def forward(self, x):
        x = x.view(-1, 784)  # 数据展平，并未获取空间信息，-1其实就是自动获取mini_batch
        x = F.relu(self.l1(x))
        x = F.relu(self.l2(x))
        x = F.relu(self.l3(x))
        x = F.relu(self.l4(x))
        return self.l5(x)  # 最后一层不做激活，不进行非线性变换,
        # 因为我们使用交叉熵损失计算损失CrossEntropyLoss，这里面本来就有softmax可以作为激活函数了


# 创建神经网络对象
model = Net()

# loss:交叉熵损失
# optim：经典的梯度下降法
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)


# 训练优化
def train(epoch):
    running_loss = 0.0
    # train_loader是一个dataloader数据
    for batch_idx, data in enumerate(train_loader, 0):
        # 获得一个批次的数据和标签，
        inputs, target = data

        # 获得模型预测结果(64, 10)就是(batch_size*类别总数)
        outputs = model(inputs)  # torch.Size([64, 10])
        # 交叉熵代价函数outputs(64,10),target(64)
        loss = criterion(outputs, target)  # target:torch.Size([64])

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        # 计算累计loss
        running_loss += loss.item()
        if batch_idx % 300 == 299:
            print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
            running_loss = 0.0


# 测试集
def test():
    correct = 0  # 正确样本量
    total = 0  # 总样本量
    with torch.no_grad():
        for data in test_loader:
            images, labels = data
            outputs = model(images)
            # 去除最大值表示样本预测值
            _, predicted = torch.max(outputs.data, dim=1)  # dim = 1 列是第0个维度，行是第1个维度
            total += labels.size(0)
            correct += (predicted == labels).sum().item()  # 张量之间的比较运算
    print('accuracy on test set: %d %% ' % (100 * correct / total))


if __name__ == '__main__':
    # 所有样本进行十次迭代
    for epoch in range(10):
        train(epoch)
        test()

pytorch实现多分类

数据

import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
fig = plt.figure()
n=1
for i in range(1,9):
    for j in range(1,9):
        ax = fig.add_subplot(8,8, n)
        ax.matshow(load_digits().images[n])
        n+=1
        ax.set_xticklabels([]) 
        ax.set_yticklabels([])
plt.show()

load_digits().images是88数据，load_digits().data是64的向量，即88的展开

损失计算

概率计算：

softmax

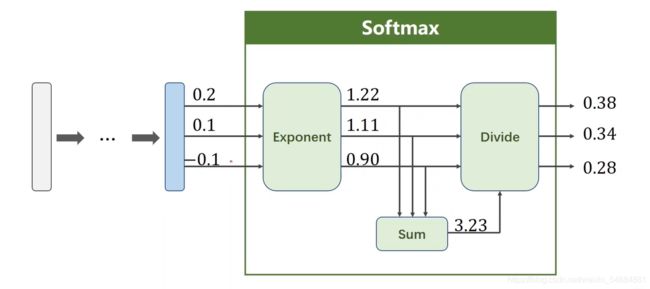
nllloss：
CrossEntropyLoss（交叉熵损失）：

代码

import torch
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split


class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        # 构建三种线性函数作为神经网络的层
        self.linear1 = torch.nn.Linear(64, 50, bias=True)
        self.linear2 = torch.nn.Linear(50, 40, bias=True)
        self.linear3 = torch.nn.Linear(40, 30, bias=True)
        self.linear4 = torch.nn.Linear(30, 20, bias=True)
        self.linear5 = torch.nn.Linear(20, 10, bias=True)
        # 用ReLU作为激活函数，在线性回归的基础之上增加模型复杂度
        self.active = torch.nn.ReLU()

    def forward(self, x):
        # 通过ReLU函数使数据具有非线性的性质
        y_pred = self.active(self.linear1(x))
        y_pred = self.active(self.linear2(y_pred))
        y_pred = self.active(self.linear3(y_pred))
        y_pred = self.active(self.linear4(y_pred))
        return self.linear5(y_pred)


def trian(epoch, x_train, y_train):
    running_loss = 0
    for batch_index in range(100):
        optimizer.zero_grad()
        result = model.forward(x_train)
        loss = criterion(result, y_train)
        loss.backward()
        optimizer.step()
        running_loss += loss.item()
        if batch_index % 100 == 100 - 1:
            print("epoch：",epoch, "loss",running_loss / len(y_train))


def text(num):
    correct = 0
    total = 0
    with torch.no_grad():
        for i in range(num):
            res = model(x_test)
            _, pred = torch.max(res.data, dim=1)
            total += y_test.size(0)
            correct += (pred == y_test).sum().item()
    print("正确率为 %d %%" % (100 * correct / total))


# 数据加载
digits = load_digits()

# 创建被训练的数据
x_train, x_test, y_train, y_test = train_test_split(digits.data, digits.target, test_size=0.3, random_state=0)

num = len(y_test)

x_train = torch.Tensor(x_train)
# 这里一定要注意：不是y_train.reshape(len(y_train),-1)
y_train = torch.LongTensor(y_train)
x_test = torch.Tensor(x_test)
y_test = torch.LongTensor(y_test)

# 创建对象
model = Net()
# 创建评估模型,交叉熵损失
criterion = torch.nn.CrossEntropyLoss()
# 创建迭代模型
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, amsgrad=True)

if __name__ == '__main__':
    for epoch in range(10):
        trian(epoch, x_train, y_train)
        text(num)

结果：

epoch： 0 loss 0.019410030054841293
正确率为 96 %
epoch： 1 loss 3.5717428221319885e-05
正确率为 96 %
epoch： 2 loss 1.3584361539484212e-05
正确率为 96 %
epoch： 3 loss 7.488490078387472e-06
正确率为 96 %
epoch： 4 loss 4.7920893863111725e-06
正确率为 96 %
epoch： 5 loss 3.365849437137996e-06
正确率为 96 %
epoch： 6 loss 2.4985773561696663e-06
正确率为 96 %
epoch： 7 loss 1.956557368221263e-06
正确率为 96 %
epoch： 8 loss 1.5848625324144715e-06
正确率为 96 %
epoch： 9 loss 1.3190097713484759e-06
正确率为 96 %