【Pluto SDR】基于16QAM的数字通信系统

引言

我是一名通信工程的一名大三学生。这是，第一次写小文章分享呢。以前包括现在也一直钦佩CSDN博客上一些大佬们的分享，所以这次拿着自己的期末报告来稍稍分享一下。如果以下分享有什么问题，大家可以在评论区指点哈~

上次实验我们实现了基于Pluto Radio的模拟通信系统的发送和接收，发现接收到的信号出现了畸变现象，例如高次谐波失真。是否有一种系统可以避免或忽略这种畸变现象呢？

同时，考虑到收发端存在一定的时延，接收端需要具备帧同步技术。

除此之外，还存在许多问题，接下来我们将对这些问题进行细致的讨论与解决。

数字传输通信系统模型

数字调制是现代通信的重要方法，它与模拟调制相比有许多优点。数字调制具有更好的抗干扰性能，更强的抗信道损耗，以及更好的安全性；数字传输系统中可以使用差错控制技术，支持复杂信号条件和处理技术，如信源编码、加密技术以及均衡等。

接下来的实验，我们将用数字调制系统代替模拟调制系统，进一步探究。

下图是数字通信系统模型的框图。信号从信源产生，经过信源编码、加密信道编码、数字调制，最后发送信号；在接收端也有类似的解调步骤。

由于无线电通信往往需要通过自由空间这一信道，所以基带传输无法实现，则需要进行第二种传输方式——将有用信号进过调制器，通过天线发射；将接收天线上接收到的信号通过解调器，即可得到恢复的信号，为信宿所用。

总的来说，数字通信系统的复杂度会比模拟通信系统要复杂，但是他们都在发送端和接收端具有对称性，且传输的目的就是提高信号的抗干扰能力。

对于数字传输系统，我们往往分为数字基带传输和数字带通传输。本次实验，我们利用Pluto Radio作为无线通信平台，自由空间作为信道，所以必须进行数字带通传输。

对于数字带通传输而言，其调制方式是首先需要考虑的，另外我们依然需要考虑数字信号传输过程中的码间串扰问题。
综上，我们需要建立以下子模型：数字调制模型、时间同步模型、相位补偿模型、帧同步模型等。

数字调制模型

针对我们本次实验的需求，利用现有模型——16进制正交幅度调制(16QAM)。
QAM是一种振幅和相位联合键控。在QAM体制中，信号的振幅和相位作为两个独立的参量同时收到调制。这种信号的一个码元可表示为
$$e_k(t)=A_{k}cos({\omega }_{c}t+{\theta }_k),k{T}_B\le t\le (k+1)T_B$$
式中：k为整数。
将其展开为
$$e_k(t)=X_{k}cos{\omega }_{c}t+Y_{k}sin{\omega }_{c}t$$
其中令
$$X_k=A_{k}cos{\theta }_k,Y_k=-A_{k}sin{\theta }_k$$
若 值仅可以取$\pi /4$和$-\pi /4$，则 仅可以取$A$和$-A$ ，由此QAM信号成为了QPSK信号。因此，QPSK是一种最简单的QAM信号，典型的QAM信号有16进制的，记为16QAM。
对于16QAM映射即可通过上式(2)，且设k=4。可利用其矢量图（即星座图）来观察映射分布情况。

帧同步模型

在数字时分多路通信系统中，为了能正确分离各路时隙信号，在发送端必须提供每帧的起始标记，在接收端检测并获取这一标志的过程称为帧同步。

帧同步有起止式同步法和插入特殊同步码组法两种。
起止式同步法：是在发送端利用特殊的码元编码规则使码组本身自带分组信息。
插入特殊同步码组法：是指在发送码元序列中插入用于帧同步的若干同步码．主要有集中式插入和间隔式插入两种。

这里我们对集中式插入特殊同步码组进行进一步讨论。集中式插入，也称为连贯式插入，要求帧同步特殊码组具有优良的自相关特性。常用的帧同步码组是巴克码。

巴克码序列是相位编码信号的一种，具有理想的自相关特性。巴克码的自相关函数的主峰和旁瓣均为底边宽度为2T的等腰三角形，主瓣峰值是旁瓣峰值的13倍。能够找到的巴克码只有7种，子脉冲长度分别为：2，3，4，5，7，11，13。已经证明巴克码的最大长度为13位。其中，它的自相关函数如下式：
$$R_j={\Sigma }_{1-1}^{N-j}{X}_i{X}_{i+j}$$

相位同步模型

由于对于一帧数据而言，传输时间非常短，可以理解为一帧数据经过了一个恒参信道。所以，这一帧数据整体被相移了一个共同未知的相角，如下式。
$$S_R(t)=H(\varphi )(S(t)+n(t))$$
其中
$$H(\varphi )=|H(\varphi )|e^{-j\varphi }$$
上式可以理解为一个已调信号S(t) 经过一个恒参信道，被加性噪声n(t) 污染，同时在传输过程中产生了相移和增益衰减。

所以，对于接收端而言，我们需要根据发送数据中的信息标志来相位估计，并达到相位补偿的目的。

在帧同步的模型中，我们已经提及了巴克码等帧同步码。它不仅可以用于帧同步，而且可以用于相偏补偿。
$$\tilde{H}(\varphi )=\frac{H(\varphi )(S(t)+n(t))}{S(t)}=\lambda H(\varphi )=e^{-j\varphi }|\tilde{H}(\varphi )|$$
通过同步码对应位相除并求和，即可得到相位信息。

时间同步模型

针对时间同步的问题，我们可以通过过采样来获得相对准确的符号信息。

当然当下也有一些通过差值运算来实现的同步模型，此处不作展开分析。

基于SDR的数字通信系统

首先，将要传输的数据，例如正弦波，模拟信号数字化，将其量化为4个电平，即16进制。
根据16QAM，将信号映射为复信号，如下图。

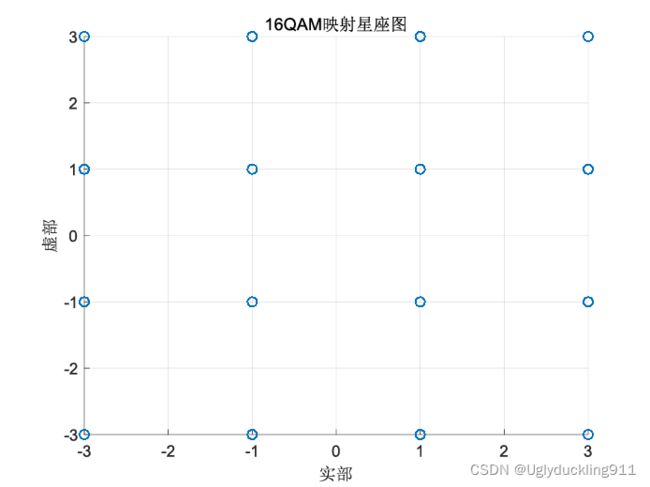
根据映射波形，实部和虚部都被量化为了四个电平；根据映射星座图，散点被均匀且聚类在了16个星座位置。无论是映射波形，还是映射星座图，均能反映出映射情况。

为了实现无码间串扰，需要在发射端和接收端设计根升余弦滤波器，将滤波器各项参数设置如下：

• 发送端根升余弦滤波器八倍过采样；
• 接收端根升余弦滤波器八倍下采样；两个滤波器的滚降系数均设为0.6；

以下为经过发送端根升余弦滤波器的信号如下。

上图发现，整体的序列长度被拉长，符合八倍过采样的设置；前面部分信号为同步码，此实验利用13位巴克码信号。

然后将数据运载在Pluto Radio，设置发送端和接收端的载频同步：

• 中心频率为2.5GHz；
• 基带采样速率为1MHz；
• 设置接收机中心频率增益来源为手动，并设置接收机增益为40dB，发射机增益为0dB；
• 设置接收机每次接收数据的采样数目，根据发送数据的点数而定；

选择接收端的增益平稳数据，对数据进行以下进一步分析。

首先进行根升余弦滤波器处理，实现无码间串扰。输出波形如下图波形

比对发送和接受前后波形，此时的波形依然存在较大失真现象。

由于我们依然位置一帧数据的起始位置。所以，我们需要根据同步码对信号进行定位处理。利用已知的巴克码序列与接收的信号进行相关性分析。

从上图发现，一段数据中存在一个尖峰脉冲，即该脉冲相关性极高，为一帧数据的起始位置。由此，我们可以利用该信息，提取出一帧数据。

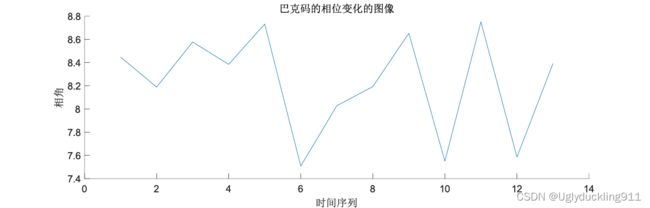
除此之外，巴克码所在位置的相位偏移信息也可以通过同步码来进行估计。以下为巴克码所在位置的相位偏移情况。

利用该相位偏移信息，可计算相位偏移角度为8.2301度。

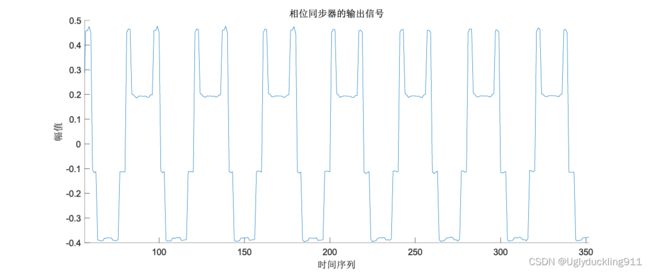
由此可获得相位同步后的信号

上图，明显发现此时的信号所呈现的4电平分别更加鲜明了。

由于信号在传输过程中出现了衰弱现象，所以我们需要对信号进行功率均衡，通过评估信号的平均功率，对其功率进行补偿处理。下图是功率补偿后的波形图和星座图。

功率均衡后整体波形幅度增大，但相对波形未有变化；星座图呈现较好的集群分布，且每个集群点均匀分布在各个星座点周围。

对以上信号16QAM反向映射，即可得到发送端调制信号。

解调后的信号与原始数据完全吻合，传递误码率为0。

总结与分析

综上实验，我们实现了一个基于Pluto Radio和MATLAB平台的简易数字通信系统。

本次实验实现的数字通信系统，包含了时间同步、相位同步、帧同步、功率均衡等一系列功能；传输误码率为0。

本次实验为将来学习数字通信系统有了更加深入的理解。

代码

以下是发送端的MATLAB代码

%%
%初始化
clc;clear;
tx = sdrtx('Pluto','CenterFrequency',2.5e+09,...
    'BasebandSampleRate',1e6,...
    'Gain',0);
rx = sdrrx('Pluto','CenterFrequency',2.5e+09,...
    'OutputDataType','double',...
    'BasebandSampleRate',1e6,...
    'SamplesPerFrame',100000,...
    'GainSource','Manual',...
    'Gain',40);
sps = 8; 											%采样次数
k = 4; 												%电平数
M = 2^k; 											%调制阶数
normalize_factor = sqrt(10); 						%功率因子（手动
Rolloff = 0.6; 										%滚降系数
NormalizedLoopBandwidth = 0.1; 						%规范化的环路带宽
synWord = k*[1;1;1;1;1;-1;-1;1;1;-1;1;-1;1]; 		%校验码
waitWord = zeros(5,1); 								%收发间歇码
N = 0; 												%图像显示数目
%正弦信号
t = pi/20:pi/20:pi*40;
Data_sin = round((M-1)/2*sin(t)+(M-1)/2);
Data = Data_sin'; 									%有用信号
T = length(Data); 									%有用信号长度
%16QAM映射
mod = comm.RectangularQAMModulator(M); 				%16QAM调制器
Data_mod = mod(Data);
N = N+1;figure(N);hold on; 							%映射图像
plot(real(Data_mod),'b-');
plot(imag(Data_mod),'r:');
xlabel("时间序列");ylabel("幅值");
legend("实部","虚部");
title("16QAM映射波形图");
%星座图
N = N+1;figure(N);hold on;grid on					%映射图像
scatter(real(Data_mod),imag(Data_mod));
xlabel("实部");ylabel("虚部");
title("16QAM映射星座图");
%合成一帧数据包
Tdata = [synWord;Data_mod;waitWord];
%根升余弦滤波器
txFilt = comm.RaisedCosineTransmitFilter(...      	%根升余弦滤波器对象
'OutputSamplesPerSymbol',sps,...                  	%八倍采样的滤波器
    'RolloffFactor',Rolloff);
Tdata_F = txFilt(Tdata);      
% N = N+1;figure(N);hold on; 					  	%滤波后图像
% plot(real(Tdata_F),'b-');
% plot(imag(Tdata_F),'r:');
% xlabel("时间序列");ylabel("幅值");
% legend("实部","虚部");
% title("发送端根升余弦滤波器的输出信号");

%Pluto反复发送数据
tx.transmitRepeat(Tdata_F);

%接收数据
for k=1:3
    rx();
end
Rx_Sig = rx();
% release(tx); 									  	%释放Pluto
%%
%根升余弦滤波器
rxFilt = comm.RaisedCosineReceiveFilter(...
    'InputSamplesPerSymbol',sps,...
    'DecimationFactor',1,...
    'RolloffFactor',Rolloff);
Rx_Sig_F = rxFilt(Rx_Sig);
% N = N+1;figure(N);hold on;					  	%滤波后图像
% plot(real(Rx_Sig_F),'b-');
% plot(imag(Rx_Sig_F),'r:');
% xlabel("时间序列");ylabel("幅值");
% legend("实部","虚部");
% title("接收端根升余弦滤波器的输出信号");

%%
%时间同步
symsync = comm.SymbolSynchronizer(...             	%这里的参数都可以调节
    'TimingErrorDetector','Gardner (non-data-aided)',...
    'NormalizedLoopBandwidth',NormalizedLoopBandwidth,...
    'DampingFactor',2,...
    'SamplesPerSymbol',sps);
Rx_Syn = step(symsync,Rx_Sig_F);                    
% N = N+1;figure(N);hold on; 					  	%时间同步后图像
% plot(real(Rx_Syn),'b-');
% plot(imag(Rx_Syn),'r:');
% xlabel("时间序列");ylabel("幅值");
% legend("实部","虚部");
% title("时间同步器的输出信号");
%%
%相位同步
data0 = synWord(end:-1:1);
data_conv = conv(data0,Rx_Syn );
% N = N+1;figure(N);hold on; 					  	%卷积和图像
% plot(abs(data_conv))
%  xlabel("时间序列");
%  ylabel("相关度")
%  title("相关性分析图像")
[data_conv_max , data_conv_max_addr] = max(abs(data_conv(1:end-T))); %卷积最大值
data_addr = data_conv_max_addr(1) - length(data0); %同步字段的起始位置
phase_offset = Rx_Syn (data_addr + 1: data_addr+length(data0))./synWord;     %同步字段的相位偏差
phi_offset = atan(imag(phase_offset)./real(phase_offset))/pi*180; %同步字段的相角偏差
if(mean(phi_offset)>0&mean(abs(phi_offset))>90*0.9) phi = abs(phi_offset);%相位临界处横跳矫正
else if(mean(phi_offset)<0&mean(abs(phi_offset))>90*0.9) phi = -abs(phi_offset);
    else if(mean(abs(phi_offset))<90*0.9) phi = phi_offset;
        end
    end
end
% N = N+1;figure(N);hold on;                      	%相位随之间变化的图像
% plot(phi);
% xlabel("时间序列");
% ylabel("相角")
% title("巴克码的相位变化的图像")
% e_phase = mean(phase_offset)/mean(abs(phase_offset));%利用e^jphi均值来纠正相位
e_phase = mean(real(phase_offset))/mean(abs(real(phase_offset)))*exp(1j*mean(phi*pi/180));%利用phi均值来纠正相位
R_Phase_Syn = 1/e_phase*Rx_Syn ...
    (data_conv_max_addr(1) + 1:...
    data_conv_max_addr(1)+ T);						%挑选一帧数据并相位同步
N = N+1;figure(N);hold on; 							%相位同步后图像
plot(real(R_Phase_Syn));
xlabel("时间序列");ylabel("幅值");
title("相位同步器的输出信号");
%%
%绘制星座图
Rdata = R_Phase_Syn;
Rdata =  normalize_factor*R_Phase_Syn./sqrt(mean(abs(R_Phase_Syn).^2));           %功率归一化方式一：利用所有有用信号的绝对值均值，无误码率100%
% FrameHead = Rx_Syn (data_addr + 1: data_addr+length(data0));
% normalize_factor = sqrt(mean(imag(FrameHead).^2+real(FrameHead).^2)/mean(synWord.^2));%功率归一化因子
% normalize_factor = mean(abs(FrameHead.*synWord))/mean(abs(synWord.*synWord));
% Rdata = 1/(normalize_factor)*Rdata; %功率归一化方法二：利用巴克码功率变化比来调节，无误码率90%多，星座图偏大
cd = comm.ConstellationDiagram(...
 'ReferenceConstellation',constellation(mod), ...
    'XLimits',[-5 5],'YLimits',[-5 5]);
% cd(Rdata); 										%星座图
% %星座图
% N = N+1;figure(N);hold on;grid on					%映射图像
% scatter(real(Rdata),imag(Rdata));
% xlabel("实部");ylabel("虚部");
% title("功率均衡后星座图");
% N = N+1;figure(N);hold on; 						%时间同步后的一帧数据图像
% plot(real(Rdata),'b-');
% plot(imag(Rdata),'r:');
% legend("实部","虚部");
% title("功率均衡后的一帧数据");
%%
%解调
hDemod = comm.RectangularQAMDemodulator('ModulationOrder',M);
Rdemod = hDemod(Rdata);
percentage = length(find(Rdemod==Data))/length(Data)*100;
fprintf("正确率 %.2f %%",percentage);
N = N+1;figure(N);hold on; 							%解调后数据图像
plot(real(Rdemod),'b','linewidth',2);
plot(real(Data),'r');
legend("接收","发送");
title("解调后数据与原始数据比较");
% save tmp3.mat Tdata R_Phase_Syn Rdata