层次聚类python实现_聚类算法之层次聚类(Python实现)
起步
层次聚类( Hierarchical Clustering )是聚类算法的一种,通过计算不同类别的相似度类创建一个有层次的嵌套的树。
层次聚类算法介绍
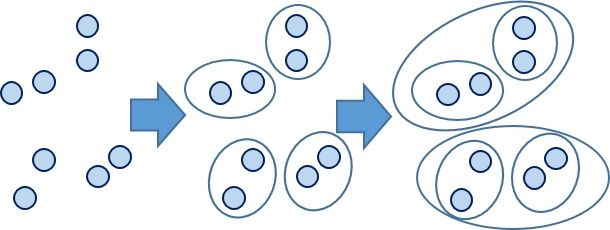
假设有 n 个待聚类的样本,对于层次聚类算法,它的步骤是:
步骤一:(初始化)将每个样本都视为一个聚类;
步骤二:计算各个聚类之间的相似度;
步骤三:寻找最近的两个聚类,将他们归为一类;
步骤四:重复步骤二,步骤三;直到所有样本归为一类。
整个过程就是建立一棵树,在建立的过程中,可以在步骤四设置所需分类的类别个数,作为迭代的终止条件,毕竟都归为一类并不实际。
聚类之间的相似度
聚类和聚类之间的相似度有什么来衡量呢?既然是空间中的点,可以采用距离的方式来衡量,一般有下面三种:
Single Linkage
又叫做 nearest-neighbor ,就是取两个类中距离最近的两个样本的距离作为这两个集合的距离。这种计算方式容易造成一种叫做 Chaining 的效果,两个 cluster 明明从“大局”上离得比较远,但是由于其中个别的点距离比较近就被合并了,并且这样合并之后 Chaining 效应会进一步扩大,最后会得到比较松散的 cluster 。
Complete Linkage
这个则完全是 Single Linkage 的反面极端,取两个集合中距离最远的两个点的距离作为两个集合的距离。其效果也是刚好相反的,限制非常大。这两种相似度的定义方法的共同问题就是指考虑了某个有特点的数据,而没有考虑类内数据的整体特点。
Average Linkage 这种方法就是把两个集合中的点两两的距离全部放在一起求均值,相对也能得到合适一点的结果。有时异常点的存在会影响均值,平常人和富豪平均一下收入会被拉高是吧,因此这种计算方法的一个变种就是取两两距离的中位数。
python 实现层次聚类
空间中点的距离使用欧式距离:
import math
import numpy as np
def euler_distance(point1: np.ndarray, point2: list) -> float:
"""
计算两点之间的欧拉距离,支持多维
"""
distance = 0.0
for a, b in zip(point1, point2):
distance += math.pow(a - b, 2)
return math.sqrt(distance)
定义聚类数的节点:
class ClusterNode(object):
def __init__(self, vec, left=None, right=None, distance=-1, id=None, count=1):
"""
:param vec: 保存两个数据聚类后形成新的中心
:param left: 左节点
:param right: 右节点
:param distance: 两个节点的距离
:param id: 用来标记哪些节点是计算过的
:param count: 这个节点的叶子节点个数
"""
self.vec = vec
self.left = left
self.right = right
self.distance = distance
self.id = id
self.count = count
vec 表示合并后的聚类中心,是一个点,代表整个聚类的位置;distance 表示左节点和右节点的距离。
计算层次聚类算法的类:
class Hierarchical(object):
def __init__(self, k = 1):
assert k > 0
self.k = k
self.labels = None
def fit(self, x):
nodes = [ClusterNode(vec=v, id=i) for i,v in enumerate(x)]
distances = {}
point_num, future_num = np.shape(x) # 特征的维度
self.labels = [ -1 ] * point_num
currentclustid = -1
while len(nodes) > self.k:
min_dist = math.inf
nodes_len = len(nodes)
closest_part = None # 表示最相似的两个聚类
for i in range(nodes_len - 1):
for j in range(i + 1, nodes_len):
# 为了不重复计算距离,保存在字典内
d_key = (nodes[i].id, nodes[j].id)
if d_key not in distances:
distances[d_key] = euler_distance(nodes[i].vec, nodes[j].vec)
d = distances[d_key]
if d < min_dist:
min_dist = d
closest_part = (i, j)
# 合并两个聚类
part1, part2 = closest_part
node1, node2 = nodes[part1], nodes[part2]
new_vec = [ (node1.vec[i] * node1.count + node2.vec[i] * node2.count ) / (node1.count + node2.count)
for i in range(future_num)]
new_node = ClusterNode(vec=new_vec,
left=node1,
right=node2,
distance=min_dist,
id=currentclustid,
count=node1.count + node2.count)
currentclustid -= 1
del nodes[part2], nodes[part1] # 一定要先del索引较大的
nodes.append(new_node)
self.nodes = nodes
self.calc_label()
def calc_label(self):
"""
调取聚类的结果
"""
for i, node in enumerate(self.nodes):
# 将节点的所有叶子节点都分类
self.leaf_traversal(node, i)
def leaf_traversal(self, node: ClusterNode, label):
"""
递归遍历叶子节点
"""
if node.left == None and node.right == None:
self.labels[node.id] = label
if node.left:
self.leaf_traversal(node.left, label)
if node.right:
self.leaf_traversal(node.right, label)
最后将聚类的列表标记保存于 labels 中。
测试
与 sklearn 进行对比:
iris = datasets.load_iris()
my = Hierarchical(4)
my.fit(iris.data)
print(np.array(my.labels))
sk = cluster.AgglomerativeClustering(4)
sk.fit(iris.data)
print(sk.labels_)
得到输出:
[3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3 3 3 3 3 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 0 1 2 1 2 2 2 2 1 2 2 2 2
2 2 1 1 2 2 2 2 1 2 1 2 1 2 2 1 1 2 2 2 2 2 1 2 2 2 2 1 2 2 2 1 2 2 2 1 2
2 1]
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 3 2 3 2 3 2 3 3 2 3 2 3 2 3 3 2 3 2 2 2 2
2 2 2 0 2 3 3 3 3 2 3 2 2 2 3 3 3 2 3 3 3 3 3 2 3 3 0 2 0 0 0 0 3 0 0 0 0
0 0 2 2 0 0 0 0 2 0 2 0 2 0 0 2 2 0 0 0 0 0 2 2 0 0 0 2 0 0 0 2 0 0 0 2 0
0 2]
结果还算是理想的。
层次聚类的优缺点
优点:
一次性得到聚类树,后期再分类无需重新计算;
相似度规则容易定义;
可以发现类别的层次关系。
缺点:
计算复杂度高,不适合数据量大的;
算法很可能形成链状。
附录