(系列笔记)21.KMeans聚类算法
文章目录
- KMeans——最简单的聚类算法
-
- 什么是聚类(Clustering)
- 常用的几种距离计算方法
-
-
-
- 欧氏距离(又称2-norm距离)
- 余弦距离(又称余弦相似性)
- 曼哈顿距离(Manhattan Distance, 又称 1-norm 距离)
-
- 其他距离
-
-
- KMeans
-
-
- 什么是KMeans
- 算法步骤
- 计算目标和细节
-
-
- 目标
- 分配
- 更新
-
- 启发式算法
-
- 实例对比 KNN 和 KMeans
-
-
-
- KMeans实例
- KNN实例
-
-
KMeans——最简单的聚类算法
什么是聚类(Clustering)
聚类并非一种机器学习专有的模型或算法,而是一种统计分析技术,在许多领域得到广泛应用。
广义而言,聚类就是通过对样本静态特征的分析,把相似的对象,分成不同子集(后面我们将聚类分出的子集称为“簇”),被分到同一个子集中的样本对象都具有相似的属性。
在机器学习领域,聚类属于一种无监督式学习算法。
许多聚类算法在执行之前,需要指定从输入数据集中产生的分簇的个数。除非事先准备好一个合适的值,否则必须决定一个大概值,这是当前大多数实践的现状。我们今天要讲的 KMeans 就是如此。
常用的几种距离计算方法
通常情况下,在聚类算法中,样本的属性主要由其在特征空间中的相对距离来表示。这就使得距离这个概念,对于聚类非常重要。
在正式讲解聚类算法之前,我们先来看几种最常见的距离计算方法。
欧氏距离(又称2-norm距离)
在欧几里德空间中,点 x = ( x 1 , . . . , x n ) x=(x_1,...,x_n) x=(x1,...,xn)和 y = ( y 1 , . . . , y n ) y=(y_1,...,y_n) y=(y1,...,yn)之间的欧氏距离为:
![]()
在欧几里得度量下,两点之间线段最短。
余弦距离(又称余弦相似性)
两个向量间的余弦值可以通过使用欧几里德点积公式求出:
![]()
所以:

也就是说,给定两个属性向量A和B,其余弦距离(也可以理解为两向量夹角的余弦)由点积和向量长度给出,如下表示:

这里的 A i A_i Aih和 B i B_i Bi分别代表向量A和B的各分量。给出的余弦相似性范围从-1到1:
- -1意味着两个向量指向的方向截然相反;
- 1表示它们的指向是完全相同的;
- 0则表示它们之间是独立的;
- [-1,1]之间的其他值则表示中间成都的相似性或相异性。
曼哈顿距离(Manhattan Distance, 又称 1-norm 距离)
曼哈顿距离的定义,来自于计算在规划为方型建筑区块的城市(如曼哈顿)中行车的最短路径。
假设一个城市是完备的块状划分,从一点到达另一点必须要沿着它们之间所隔着的区块的边缘走,没有其他捷径(如下图):

因此,曼哈顿距离就是:在直角坐标系中,两点所形成的线段对x 和 y 轴投影的长度总和。
从点 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)到点 ( x 2 , y 2 ) (x_2,y_2) (x2,y2),曼哈顿距离为:

其他距离
除了上述最常用的几种距离之外,还有其他多种距离计算方法,例如:Infinity norm(又称 Uniform norm,一致范式)、马氏距离、汉明距离(Hamming Distance)等。
在本课的例子中,计算距离时,如无特别说明,采用的都是欧氏距离。
KMeans
什么是KMeans
简单来说,KMeans 是一种聚类方法,k是一个常数值,由使用者指定,这种算法负责将整个特征空间中的n个向量聚集到k个簇中。
比如,下图就是一个k=3的KMeans算法聚类前后的情况。
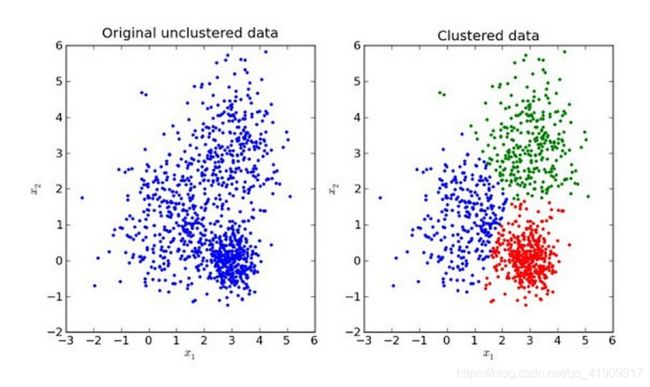
算法步骤
- Step 0:用户确定k值,并将n个样本投射为特征空间(一般为欧式空间)中的n个点( k ≤ n k \le n k≤n);
- Step 1:算法在这n个点钟随机取k个点,作为初始的“簇核心”;
- Step 2:分别计算每一个样本点到k个簇核心的距离(这里的距离一般取欧氏距离或余弦距离),找到离该点最近的簇核心,将它归属到对应的簇;
- Step 3:所有点都归属到簇之后,n个点就分为了k个簇。之后重新计算每个簇的重心(平均距离重心),将其定位新的“簇核心”;
- Step 4:反复迭代Step2 - Step3,直到簇核心不再移动为止。
算法的执行过程可用下图直观表达:
计算目标和细节
上面给出的Step3在一次各个点归入簇中的迭代完成后,要重新计算这个簇的重心位置。
重心位置是根据簇中每个点的平均距离来计算的。这个平均距离如何算出?
要明确算法细节,首先要搞清楚 KMeans 算法的目标——在用户提供了k值之后,以一种什么样的原则来将现有的n个样本分成k簇才是最理想的?
目标
有n个样本( x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn),每个都是d维实向量,KMeans聚类的目标是将它们分为k个簇( k ≤ n k \le n k≤n),这些簇表示为 S = ( S 1 , S 2 , . . . , S k ) S=(S_1,S_2,...,S_k) S=(S1,S2,...,Sk)
Kmeans算法的目标是使得簇内平方和(Within-cluster Sum of Squares,WCSS )最小:

其中 μ i \mu_i μi是 S i S_i Si的重心。
分配
Step2 又叫做分配(Assignment)。
设此时为时刻t,t时刻 S i S_i Si的簇核心为 μ i ( t ) \mu_i^{(t)} μi(t)。将某个样本点 x p x_p xp归入到簇 S i ( t ) S_i^{(t)} Si(t)的原则是:它归入该簇后,对该簇WCSS的贡献最小:

因为WCSS等于簇中个点到该簇核心的欧氏距离平方和,又因为在每次进行Step2之前,我们已经认定了当时所有簇的簇核心 μ i ( t ) \mu _i^{(t)} μi(t),i=1,2,…,k已经存在。因此只要把 x p x_p xp分配到离他最近的簇核心即可。
注意:尽管在理论上 x p x_p xp可能被分配到2个或更多的簇,但在实际操作中,它只被分配给一个簇。
更新
Step3又叫做更新(update),这一步要重新求簇核心,具体计算非常简单,对于该簇中的所有样本求均值就好:
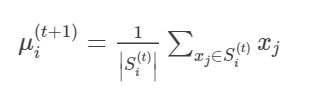
其中 ∣ S i ∣ |S_i| ∣Si∣表示 S i S_i Si中样本的个数。
启发式算法
启发式算法(Huristic Algorithm):是一种基于直观或经验构造的算法。相对于最优化算法要求得待解决问题的最优解,启发式算法力求在可接受的花费(消耗的时间和空间)下,给出待解决问题的一个可行解,该可行解与最优解的偏离程度一般不能被预计。
启发式算法常能发现不错的解,但也没法证明它不会得到教坏的解;它通常可在合理时间解出答案,但也没办法知道它是否没次都可以这样的速度求解。
虽然有种种不确定性,且性能无法得到严格的数学证明,但启发式算法直观,简单,易于实现。即使在某些特殊情况下,启发式算法会得到很坏的答案或效率极差,然而造成那些特殊情况的数据组合,也许永远不会在现实世界出现。因此现实世界中启发式算法常用来解决问题。
上面我们讲的是最常见的用于实现KMeans的启发式算法:Lloyd’s算法。
Lloyd’s算法是一种很搞笑的算法,通常情况,它时间复杂度是O(nkdi),其中n为样本数,k为簇数,d为样本维度数,而i为从开始到收敛的迭代次数。
如果样本数据本身就有一定的聚类结构,那么收敛所需的迭代次数通常是很少的,而且一般前几十次迭代之后,再进行迭代,每次的改进就很小了。
因此,在实践中,Lloyd’s算法往往被认为是线性复杂度的算法,虽然在最糟糕的情况下时间复杂度是超多项式(Superpolynomial)的。目前,Lloyd’s算法是KMeans聚类的标准方法。
当然,每一次迭代它都要计算每个簇中各个样本到簇核心的距离,这是很耗费算力的。不过好在大多数情况下,经过头几轮的迭代之后,各个簇就相对稳定了,大多数样本都不会再改变簇归属,可以利用缓存和三角形公理来简化后续计算。
【局限】
KMeans简单直观,有了启发式算法后,计算复杂度也可以接受,但存在以下问题:
- k值对最终结果的影响至关重要,而它却必须要预先给定,给定合适的k值,需要先验知识,凭空估计很困难,或可能导致效果很差。
- 初试簇核心一般是随机选定的,偏偏它们又很重要,几乎可以说是算法敏感的,一旦选择不合适,可能只能得到局部最优解,而无法得到全局的最优解,当然,这也由KMeans算法本身的局部最优性决定的。
这也就造成了KMeans的应用局限,使得它并不适合所有的数据。例如对于非球形簇,或者多个簇之间尺寸和密度相差较大的情况,KMeans就处理不好了。
实例对比 KNN 和 KMeans
KMeans实例
其中训练样本是10个人的身高(cm)、体重(kg)数据:
from sklearn.cluster import KMeans
import numpy as np
import matplotlib.pyplot as plt
X = np.array([[185.4, 72.6], [155.0, 54.4], [170.2, 99.9], [172.2, 97.3], [157.5, 59.0], [190.5, 81.6], [188.0, 77.1], [167.6, 97.3], [172.7, 93.3], [154.9, 59.0]])
kmeans = KMeans(n_clusters=3, random_state=0).fit(X)
y_kmeans = kmeans.predict(X)
centroids = kmeans.cluster_centers_
plt.scatter(X[:, 0], X[:, 1], s=50);
plt.yticks(())
plt.show()
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')
plt.scatter(centroids[:, 0], centroids[:, 1], c='black', s=200, alpha=0.5);
plt.show()
训练输入如下:

KMeans聚类后:

我们可以预测一下两个新样本:
print(kmeans.predict([[170.0, 60], [155.0, 50]]))
【输出】:[1 1]
1对应的是哪个簇:print(y_kmeans)
【输出】:[0 1 2 2 1 0 0 2 2 1]
课件,1对应是左下角的那个。
KNN实例
同样的问题,如果我们要用 KNN 来解决,应该如何呢?我们指望只输入原始身高体重数据是不够的,还必须要给每组数据打上标签,将标签也作为训练样本的一部分。如何打标签呢?我们就用上面 KMeans 的输出好了:
from sklearn.neighbors import KNeighborsClassifier
X = [[185.4, 72.6],
[155.0, 54.4],
[170.2, 99.9],
[172.2, 97.3],
[157.5, 59.0],
[190.5, 81.6],
[188.0, 77.1],
[167.6, 97.3],
[172.7, 93.3],
[154.9, 59.0]]
y = [0, 1, 2, 2, 1, 0, 0, 2, 2, 1]
neigh = KNeighborsClassifier(n_neighbors=3)
neigh.fit(X, y)
然后我们也来预测和 KMeans 例子中同样的新数据:print(neigh.predict([[170.0, 60], [155.0, 50]]))
【结果】:[1 1]
