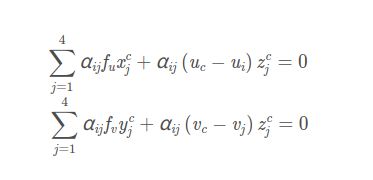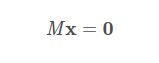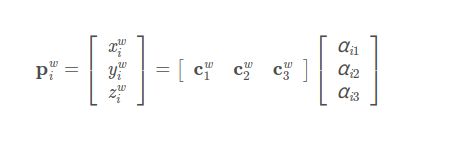SLAM学习笔记（十六）快速了解EPnP算法原理

前几天有实习的学弟询问我关于2D-3D匹配点的EPnP的算法原理。一下子问到还真没想起来。看了看资料，回忆起来了，特在这里简单的总结一下。

学弟没看明白的原因，其实就是一些相关的讲解文章一上来就摆出让人生畏的一堆公式。其实个人觉得在目前Epnp算法已经被集成到OpenCV中库函数里面，我们就没必要再去手动实现轮子，因此求解的细节不需要死记，我们只要知道每一步是在干什么就可以了。除非你要研究和改进算法本身，那就直接去阅读原论文是最好的。

如果只是想知道EPNP是怎么个思路和流程，但是高翔的书里没讲，自己网上搜了一下却被各种公式和控制点表示弄的晕头转向的话，那可以看看我的文章，希望能帮到各位。

很多人搞不明白主要是被好多求解的中间过程绕晕了，其实EPNP最重要的不是某个东西怎么求解，而是为什么要求解某个东西。因此我这里删繁就简，先说为什么，每一步在干什么，最后再说求解的细节问题。

---

先复习一下：学过SLAM14讲的人应该知道，求解2D-3D的匹配问题主要基于PNP算法，求解PnP算法的主要方式大致是直接线性变换（DLT），P3P，EPnP，UPnP以及非线性优化方法。

DLT主要是通过构建一个增广矩阵（R|t），然后通过投影矩阵构建一个方程：

通过最后一行，消去s，最后构建一个12维的线性方程组，通过6对匹配点（一对点两个方程）来求解中间的矩阵。

这种方式是通过2D-3D的关系直接构建方程，直接求解。

但是其实我们可以不采用这种方式，而是采用一种变换的形式，把2D-3D匹配关系，变换成3D-3D点的匹配关系。这样不就可以求解ICP或者是非线性优化方式去求解了吗？

P3P，EPNP都是通过这样的方式。

3D-3D的ICP方式我不在本文中介绍，感兴趣的可以看一下，我之前有写过一个总结：SLAM14讲学习笔记（四）视觉里程计（特征点法）和重难点总结

相信看过视觉SLAM14讲的人都了解ICP算法的过程，因此我不重复叙述了。这篇文章我只讲怎么把2D到3D的匹配过程，变成3D-3D的匹配过程。

P3P方法，即通过三个点的几何关系，用余弦定理联立方程，是一个几何的方式。

而EPnP，是通过一个“中间介质”，即“控制点”来变换的。（很多人看了会觉得疑惑，为什么要这样，有什么用？这就是我这里讲解的重点）

首先，我们要确定一个公式，即，空间内的任意一个三维坐标点，可以用四个控制点来加权表示。

我们首先要指出，控制点是我们自己人为去找到的。怎么找到控制点？为了不要影响整体思路，我们先把这个点记下来，记作待解决的问题【1】。我在讲完思路以后，下文再说。

另外，为什么为什么非要四个控制点，三个控制点为什么不行？这个也放到后面说，我们把它记作待解决的问题【2】。

总之，看到这里我们先假设我们通过某个方式找到了四个控制点。回到上面的方程里：

四个权重的α，是我们要求解的内容。

我们为什么要求这些α呢？因为它是一个很重要的“中间介质”。

上标是c，代表是相机坐标系。上标是w，代表是世界坐标系。我们可以从上面得到：世界坐标系下的一个点Pw，可以通过R和t变换到相机坐标系下的点Pc；世界坐标系下的那四个控制点Cw，通过同样的R和t变换到相机坐标系下，变成了“相机坐标系下的四个控制点Cc”。那么权重α是不变的。

也就是说，Pw和“四个世界坐标系下的控制点Cw”服从的权重关系α，和Pc和“四个相机坐标系下的控制点Cc”所服从的权重关系α是同一个α。

那么，在之前的这个公式里，Pw是已知的（即3D-2D当中的3D匹配点），而控制点Cw也是已知的（通过某种方法选出来的），那么只有四个α是未知的。那么这个公式，主要是想要算出这个α。

怎么算？为了不要影响整体思路，我们把这个问题记作待解决的问题【3】，留到最后说。

---

总之，截至到这里，在EPNP的流程里，我们就已经通过上面的方程，求出了四个α。

那么，求出α以后要怎么用？这就不能留到最后说了，这是关键的地方。可能有的人已经想到了，这个α肯定是要用到前面推导过的式子里：

这个式子表达了相机坐标系下的坐标点和相机坐标系下的四个控制点之间的关系。

但是，我们是2D-3D的匹配点，在上面的式子里，Pc我们是不知道的，Cc我们也是不知道的。Pc本身是可以通过Pw和位姿Rt求出来，但是我们现在还不知道Rt，毕竟Rt是我们要求的内容。而如果通过像素坐标（u，v)来推，又得知道深度信息。2D-3D点的匹配，3D点的Z值是世界坐标系下的坐标值，不是相机坐标系下的深度，因此同样那个没法得到。

而Cc我们也不知道，我们只知道世界坐标系下的控制点Cw，想求Cc也得是通过Cw和Rt才能得到。因此上面的式子里，我们只知道权重α，这是我们上面已经求到的。

那么上式能不能变一下呢？

我们变成是像素坐标和相机坐标的关系。w作为深度。上面这个式子相信大家都能看明白，就是相机坐标左乘内参K，只不过相机坐标，我们用四个相机坐标系下的控制点表示了。

这个式子可以展开（自己去展，懒得展的那就直接看结果，在这个下面打公式很麻烦，因此我都找的截图），得到下面的式子：

我们看一下这个式子，α已知（上面求出来了），fu，fv是内参，uc，vc也是内参已知。ui和vi,也是已知的，就是2D-3D匹配关系中的那个2D点。

w不见了，因为这个是深度，我们不知道，因此把它消掉了。

那么这个公式里就只剩下了相机坐标系下的四个控制点的坐标未知，每个xc，yc，zc（一共4*3=12个未知数）。在这里它们作为未知数来求解。

上面两个式子可以等起来，移项，写在一边，另一边等于0。

然后这就变成了一个线性方程组：

其中M是推导后的系数，x是未知数（x就是相机坐标系下的四个控制点的坐标。注意我们最开始已知的是世界坐标系下的四个控制点坐标，那四个控制点和现在这四个本质上是同样的四个点，但是我们只知道世界坐标系下的坐标，不知道相机坐标系下的坐标）

那么求解Mx=0，就可以得到相机坐标系下的四个控制点坐标。怎么求解就不说了（线性方程不会求解吗？）

---

走到了这里，我们就得到了相机坐标系下四个控制点坐标。

再回顾一下，我们有什么，没有什么：

截至这里，我们有世界坐标系下的控制点坐标Cw（自己选择的），有世界坐标系下提取到的3D点坐标Pw，有图像坐标系下的2D坐标u和v，还知道权重α，还有刚刚求解到的相机坐标系下的四个控制点坐标Cc。

我们可以很惊喜的发现，Cw和Cc都是3D点，遵从R和t 的变换。同样，根据Cc和α，同样也能求得Pc的坐标。那么Pc和Pw同样构成一对3D-3D的匹配关系。

那么知道了3D-3D点的关系了，那这个问题就变成了求解3D-3D匹配点问题，接下来走的就是ICP算法的流程了。ICP算法我就不在这里说了，学过14讲的都知道。了解的不够深入的话可以看看我放在开头的链接。

---

好了，现在算法流程结束了。上面的流程是应该记住的，再过一下：

先选择控制点，根据3D-2D匹配对中的3D点和控制点，算出α；

然后根据这个α和3D-2D匹配对中的2D点，算出控制点在相机坐标系下的3D坐标。

最后根据3D坐标，和之前的2D-3D匹配对内的3D坐标，构建3D-3D的求解问题，用ICP来求解。

---

最后我们解决上面留下的坑，几个待解决的问题：

【1】世界坐标系下的控制点是我们自己人为去找到的。怎么找到控制点？

首先你有一堆2D-3D的控制点对，根据那些3D点，求一个重心。

这是一个求解的方法。你也可以用别的方法来求解。

【2】为什么非要4个控制点，三个为什么不行？

其实也行。但是我们用控制点，本身是想求解权重α的。假如我们用的是三个控制点：

上面如果展开成线性方程组，是三个公式，三个未知数，够了。

但是我们不要忘了还有个一个公式的：

这样四个公式，未知数却只有三个。这样的方程很难有唯一解，只有最小二乘解，这样就不准确。

因此我们用4个控制点。

【3】根据下面这个式子，怎么求出权重α？

这个感觉都不用说了，这就是四个线性方程组求解四个未知数，中学生都会解。

还有，注意了：一对3D-2D匹配点要用四个α和四个控制点。如果换成另外一对3D-2D匹配点，控制点是不变的，而α却不是刚刚的那四个α了。（之前说的α具有不变性，是指同一对2D-3D匹配点中的控制点和实际点，在相机坐标系和世界坐标系下相同，不要搞混了。）

---

最后放一下我截图来源的博客：

JesseChen79 的博客-深入EPnP算法

这个老哥写的非常好，只不过放了一大堆公式，初学者一看头都大了。

已经明白流程的建议去阅读一下，人家总结的我就不照搬了。