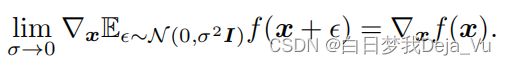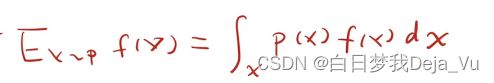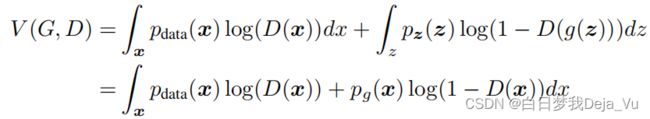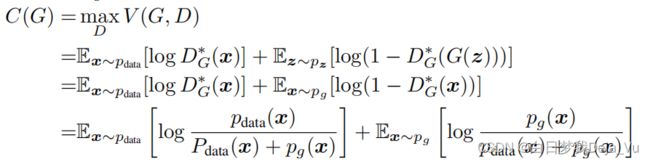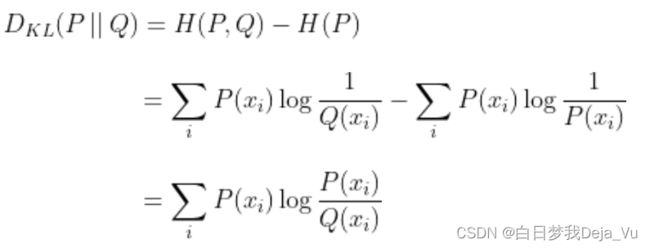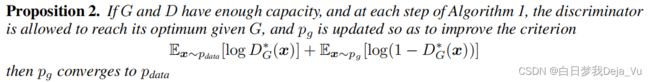GAN论文精读以及基础讲解
GAN精读论文:Neurips-2014-Generative Adversarial Nets
根据李沐老师的讲解加上笔者个人的理解做的一个笔记,希望能够对想了解GAN的求学者有所帮助!
一、标题、作者、期刊
论文的标题名为Generative Adversarial Nets,中文解释为对抗生成网络,这也能很符合其缩写GAN(干,中文谐音),是由外国深度学习也就是我们所熟知的《花书》的作者Ian J.Goodfellow所提出的,并且还有2018年图灵奖的获得者Yoshua Bengio,也是深度学习领域的一位重量级别的大佬。这篇论文分为两版,第一版发表在Arxiv上,第二版发表在Neurips中,Neurips是人工智能领域的顶级会议,与ICML并称为人工智能领域难度最大,水平最高,影响力最强的会议。
并且机器学习中有两大类
- 分辨模型:判断数据的类别或者预测实数值
- 生成模型:生成数据
二、摘要
提出了一个新的framework(框架模型)用来估计生成模型,通过对抗的过程,同时会训练两个模型生成模型G和辨别模型D。
- 生成模型G:用来抓取整个数据的分布(生成模型就是要对整个数据的分布进行建模,使得能够生成各种分布,这里的分布就是指的生成图片、文字或者电影等,在统计学中,整个世界是通过采样不同的分布来得到的,所以如果想要生成东西,就应该抓取整个数据的分布)
-
辨别模型D:用来估计样本到底是从真正的数据生成出来的还是来自生成模型G生成出来的
G的训练过程是使D出错的概率最大化,生成模型尽量想让辨别模型犯错(生成模型一般是尽量使数据分布接近,但是这个地方有所不同,它是想让辨别模型犯错)
并且这个framework对应的是minmax two-player game(博弈论中一个很有名的两人对抗游戏)在任何函数空间的 G 和 D 中存在一个独一无二的解( G 能够将数据的真实分布找出来,如果已经把真实数据发掘出来的,辨别模型 D 就做不了什么事情了),如果 G 和 D 是MLP(多层感知器)的话,那么整个系统就可以通过误差的反向传播来进行训练不需要使用任何马尔科夫链或着说对一个近似的推理过程展开,相比其他方法更加简单,而且实验效果非常好。通过对生成的样本进行定性和定量评价,实验证明了该框架的潜力。
三、 导言
深度学习是用来发现一些丰富的有层次的模型,这些模型能够对AI中各种应用的各种数据做概率分布的表示深度学习不仅仅是深度神经网络,更多的是对整个数据分布的特征表示,深度神经网络只是其中的一个手段虽然深度学习在辨别模型上取得了很大进展,但是在生成模型上做的还是比较差(难点在于在最大化似然函数的时候要对概率分布进行很多近似,这个近似的计算比较困难)深度学习在生成模型上进展不大,是因为要去近似概率分布分布来计算似然函数,这篇文章的关键是不用近似似然函数而可以用别的方法来得到一个计算上更好的模型
在所提出的对抗性网络框架中,生成模型与对手对抗:辨别模型,其学习以确定样本是来自模型分布还是来自数据分布。生成模型可以被认为类似于一组伪造者团队,试图制造假币并在不被发现的情况下使用它,而判别模型类似于警察,试图发现假币。在这个游戏中的竞争促使两个团队改进他们的方法,直到伪造品与真品无法区分。
框架下面的生成模型是一个MLP,它的输入是一个随机的噪音,MLP能够把产生随机噪音的分布(通常是一个高斯分布)映射到任何想要拟合的分布中。同理,如果判别模型也是MLP的情况下,在这个框架下的特例叫做adversarial nets,因为两个模型都是基于MLP,所以在训练的时候可以直接通过误差的反向传递而不需要像使用马尔科夫链类似的算法来对一个分布进行复杂的采样,从而具有计算上的优势
四、相关工作
本篇所讲述的版本是GAN在neurips上的最终版本,它是一个比较新的版本在搜索的时候可能会搜索到arxiv版本,它是一个比较早期的版本,作者没有将最新的版本上传到arxiv上面,并且两个版本的主要区别就是相关工作是不一样的。在arxiv版本上面相关工作的部分其实什么都没写,写的并不多,而在neurips的版本上写了很多真正相关的工作细节。
首先阐述了其他方法所存在的问题:之前的方法是想要构造出一个分布函数出来,然后提供一些参数让他可以学习,通过最大化这些参数的对数似然函数来做这样的坏处是采样一个分布的时候计算比较困难(尤其是维度比较高的时候)因为这些方法计算比较困难,所以开展了generative machines的相关工作,不再去构造这样一个分布出来,而是去学习一个模型去近似这个分布,这两种方法是有区别的。前一种方法明确知道分布是什么,包里面的均值、方差等;后一种方法不用去构造分布,只需要一个模型去近似想要的结果就可以了,缺点是不知道最后具体的分布是什么样的,好处是计算起来比较容易。
在上式中对f的期望求导等价于对f自身求导,这也是为什么可以通过误差的反向传递来对GAN进行求解。
VAEs跟GAN非常类似通过一个辨别模型来帮助生成模型,比如说NCE也用了这样的思路,但是NCE相对来说损失函数更加复杂一点,在求解上没有GAN的性能那么好
predictability minimization(PM)算法和GAN的区别:其实GAN就是predictability minimization反过来。
adversarial examples和GAN的区别:adversarial examples是说通过构造一些和真实样本很像的假样本,能够糊弄到分类器,从而测试整个算法的稳定性。
五、模型
这个框架最简单的应用是当生成器和辨别器都是MLP的时候,生成器需要去学一个在数据x上的Pg分布,我们知道GAN主要用在图片的生成上,用图片的生成来打一个比喻,假设在打游戏,显示器是4K的一个分辨率,每秒能够输出60张图片(也就是60HZ),我要设置一个生成器,也能够生成跟游戏一样的图片,那么x就是我们每次在显示器中所看到的那个4k分辨率的图片,大概是800万像素,具体来说每一个像素是一个随机变量,那么这个x就是一个长为800万维的一个多维随机变量,x中每个值的分布都是由pg这个分布来控制的。
生成模型如何输出x
首先在一个输入分布为Pz的噪音变量z上定义一个先验,z可以认为是一个100维的向量,每一元素是均值为0,方差为1的高斯噪音
生成模型就是把z映射成x,生成模型是MLP,他有一个可以学习的参数θg
假设想要生成游戏的图片
第一种办法是反汇编游戏代码,然后利用代码就知道游戏是如何生成出来的,这就类似于构造分布函数的方法,在计算上比较困难
第二种办法是不管游戏程序是什么,(假设我们看到的是一个4K的图片,但是实际上是背后的代码控制,可能就是100个变量控制的,比如哪个人物出现在哪个位置在干什么事情)假设用一个若干维的向量就足以表达游戏背后隐藏的逻辑,再学一个映设(MLP,MLP理论上可以拟合任何一个函数,所以可以通过构造一个差不多大小的向量,然后利用MLP强行将z映射成x,使得他们相似就可以了),这种方法的好处是计算比较简单,坏处是MLP不在乎背后真正的分布是什么,而是只是每次生成一个东西,看起来相似就行了,也就是说每次看到一个图片时,很难去查看到它背后对应的z是什么东西,而只能反过来说每次随机给个z,然后看手气看运气,生成一个还像样的图形就行了
辨别器:辨别器D也是一个MLP,它也有自己可以学习的参数叫做θd,它的作用是将数据(也就是之前那个800万像素的图片)放进来之后输出一个标量,这个标量用来判断x到底是来自真实采样的数据还是生成出来的图片(以游戏为例,就是这个图片到底是来自游戏中的截图,还是生成器自己生成的图片),因为知道数据的来源,所以会给数据一个标号(如果来自真实的数据就是1,来自生成的数据就是0)
所以就采样一些数据来训练一个两类的分类器,在训练D的同时也会去训练G,G用来最小化log(1-D(G(z))),其中log(1-D(G(z)))中z 代表随机噪音,放到G中就会生成图片,假设辨别器正确的话,辨别器的输出应该为0,表示是生成的数据,这个式子最终为log1等于0,当辨别器做的很好的时候就是等于0的。
但是如果辨别器没有做好,会输出一个大于0的数,在极端情况下输出1,即辨别器百分之百地确信生成模型所生成的辨别器来自真实的数据,即判断错误。则无论无何log(1-一个大于零小于1 的数)的最终结果就会变成一个负数,在极端情况下,log0是负无穷大
所以如果要训练G来最小化log(1-D(G(z)))就意味着,训练一个G使得辨别器尽量犯错,无法区分出来数据到底是来自真实数据还是生成模型所生成的数据
我们要训练两个模型,一个叫D,一个叫G,然后我们的目标函数如图所示,这一项叫做两人的minimax游戏
V(G,D)是一个价值函数;公式右边第一项是期望,x是采样真实分布;公式右边第二项是期望,x是采样噪音分布;在D是完美的情况下,公式右边的两项应该都是等于0的;如果D不完美、有误分类的情况下,这两项因为log的关系,都会变成一个负数值;所以如果想要辨别器完美地分类这两类的话,就应该最大化D的值,最小化G,目标函数中有两个东西,一个是min,一个是max,和一般的训练步骤有所区别,一般只有一个min,或者只有一个max,这里既有min又有max,就是两个模型在相互对抗:D是尽量把数据分开,G是尽量使生成数据分不开,这个在博弈论中叫两人的minimax游戏
如果达到了一个均衡,就是D不能往前进步,G也不能往前进步了,就认为达到了均衡,这个均衡叫做纳什均衡
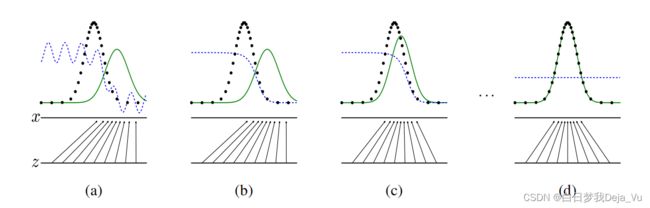
上图中一共有四张图,分别表示GAN在前面三步和最后一步所做的工作
z是一个一维的标量;x也是一个一维的标量;噪音是均匀分布采样来的;所要真实拟合的x如图中黑色圆点所示,是一个高斯分布
(a)表示第一步的时候,生成器将均匀分布进行映射,图中绿色的线就是把z映射成了一个高斯分布,此时辨别器视图中蓝色的线,表现一般
(b)表示更新辨别器,尽量把这两个东西分开,两个高斯分布的最高点表示真实分布和噪声最有可能出现的地方,辨别器需要在真实分布的地方值为1,在噪音分布的地方值为0,这样就可以尽量将来自真实分布的x和来自于生成器的x尽量分别开来
(c)表示尽量更新生成器,使得能够尽量糊弄到辨别器(就是将生成器生成的高斯分布的峰值尽量左移,向真实数据的高斯分布进行靠拢),让辨别器犯错,这时候辨别器就需要尽量调整来把这两个细微的区别区别开来。
(d)表示通过不断地调整生成器和辨别器,直到最后生成器的模型能够将来自均匀分布的随即噪音z映射成几乎跟真实分布差不多融合的高斯分布,即从真实的黑点中采样还是从生成器的绿线采样,辨别模型都是分辨不出来的(不管来自于哪个分布,辨别器对这每个值的输出都是0.5,这就是GAN最后想要的结果:生成器生成的数据和真实数据在分布上是完全分别不出来的,辨别器最后对此无能为力)
具体的算法是放在算法1中,第一行是一个for循环,每一次循环里面是做一次迭代,迭代的另一部分也是一个k步的for循环,每一步中先采样m个噪音样本,再采样m个来自真实数据的样本,组成一个两个m大小的小批量,将其放入价值函数中求梯度(就是将采样的真实样本放入辨别器,将采样的噪音放进生成器得到的生成样本放进辨别器,放进去之后对辨别器的参数求梯度来更新辨别器),这样子做k步,做完之后再采样m个噪音样本放进第二项中,把它对于生成器的模型的梯度算出来,然后对生成器进行更新,这样就完成了一次迭代
可以看到,我们每次迭代时先更新我们的辨别器,再更新我们的生成器,而且这个k是一个超参数,k不能取太小,也不能取太大,需要辨别器有足够的更新但也不要更新的太好。如果没有足够好的更新,对新的数据,生成器生成的东西已经改变了,如果辨别器没有做相应的变化,那么再更新生成器来糊弄D其实意义不大;反过来讲如果将D训练到足够完美,log(1-D(G(z)))就会变成0,对0进行求导,生成模型的更新就会有困难。
(如果辨别器是警察,生成器是造假者,假设造假者一生产假币,警察就将其一锅端了,造假者也就不会赚到钱,就没有能力去改进之后的工艺了;反过来讲,如果警察没有能力,造假者随便造点东西,警察也看不出来,也抓不到造假者,那么造假者也不会有动力去改进工艺,使得假钞和真钞真的长得差不多,所以最好是两方实力相当,最后大家能够一起进步)
k就是一个超参数,使得D的更新和G的更新在进度上差不多
外层循环迭代N次直到完成,如何判断是否收敛,这里有两项,一个是往上走(max),一个是往下走(min),有两个模型,所以如何判断收敛并不容易。整体来说,GAN的收敛是非常不稳定的,所之后有很多工作对其进行改进
在上面的公式中,等式右边的第二项存在一定的问题:在早期的时候G比较弱,生成的数据跟真实的数据差得比较远,这就很容易将D训练的特别好(D能够完美地区分开生成的数据和真实的数据),就导致log(1-D(G(z)))会变成0,它变成0的话,对他求梯度再更新G的时候,就会发现求不动了。所以在这种情况下建议在更新G的时候将目标函数改成最大化log(D(G(z)))就跟第一项差不多了,这样的话就算D能够把两个东西区分开来,但是因为是最大化的话,问题还是不大的,但是这也会带来另外一个问题,如果D(G(z))等于零的话,log(D(G(z)))是负无穷大,也会带来数值上的问题,在之后的工作中会对其进行改进
六、理论
第4章主要讲的是理论上的结果,当且仅当生成器学到的分布和真实数据的分布是相等的情况下,目标函数有全局的最优解。第二部分是我们的算法1确实能求解我们的目标函数
第一个结论:当G是固定,即生成器是固定的情况下,最优的辨别器的计算如上图公式所示
*表示最优解;Pdata表示将x放进去之后,在真实产生数据的分布中的概率是多少;Pg表示将x放进去之后,生成器所拟合的分布的概率是多少。
分布是在0和1之间的数值,所以上式中的每一项都是大于等于0、小于等于1的,因此上式中分子、分母中所有的项都是非负的,所以整个式子右式的值是在0到1之间的
当Pdata和Pg是完全相等的情况下(即对每一个x,两个p给出来的结果是一样的),右式的值是1/2,即不管对什么样的x,最优的辨别器的输出概率都是1/2,表示这两个分布是完全分不开的
单看这个结论也是非常有用的,这里可以看到D是如何训练出来的,从两个分布中分别采样出数据,用之前的目标函数训练一个二分类的分类器,这个分类器如果说给的值都是1/2,即什么值都分辨不出来,就表示这两个分布是重合的,否则的话就能够分辨出来,这个东西在统计学中非常有用,这叫做two sample test:判断两个数据是不是来自同一个分布在统计上其实有很多工具,比如说用T分布检测(在数据科学中经常使用,可以完全不管分布是什么样子的,可以无视在高维上很多统计工序不好用,就训练一个二分类的分类器,如果这个分类器能够分开这两个数据,就表示这两个数据是来自于不同分布,如果不能分开,就表示这个数据是来自同一分布的,这个技术在很多实用的技术中经常会用到它,比如说在一个训练集上训练一个模型然后把它部署到另外一个环境,然后看新的测试数据跟训练数据是不是一样的时候,就可以训练一个分类器把它分一下就行了,这样就可以避免训练一个模型部署到一个新的环境,然后新的环境和模型不匹配的问题)
接下来我们看一下证明,首先期望的计算如下图所示,E,x来自于p算一下f(x)的期望
等式右边第一项是在Pdata上面对函数求均值
等式右边第二项是在Pz上面对函数求均值
第二行,我们已知x=g(z),x是由g(z)生成出来的,假设Pg就是生成器对应的数据映射,就将g(z)替代成x,替代之后,右边第二项对z的概率求期望就变成了对x求期望,x的分布来自于生成器所对应的Pg。(我们不一定知道Pg和Pdata是什么东西也不要紧)
一旦完成替代之后,第一项和第二项是可以合并了,合并之后,积分里面的东西抽象出来(可以看出这是0、1之间的数,D(x)就是我们要求的一个东西,我们把它替换成y,将Pdata(x)替换成a,Pg(x)换成b)经过替换变量就可以得到一个关于y的函数,如果y是一个值的话,它其实是一个凸函数,取决于a、b不一样,它的形状不一样。因为它是一个凸函数,所以他会有一个最大值,因为要求最大值,所以会求导,结果是y=a/(a+b),意味着对于任何的x,最优解的D对他的输出等于y等于Pdata(x)/(Pdata(x) + Pg(x)),就证明了之前的结论
接下来将所求到的最优解代入到上图所示的价值函数中,最大化D,就是将D*直接代进去然后展开,就能得到如上图所示的结果,就能得到之前的结论,再把得到的结果写成一个关于G的函数,因为D已经求得最优解并带入了,所以整个式子就只跟G相关,所以将他记成C(G),到此对整个价值函数求解就只需要对C(G)进行最小化就行了,因为D的最优解已经算出来了
定理一是说当且仅当生成器的分布和真实数据的分布是相等的情况下,C(G)取得全局最小值的时候
为了证明这个定理,我们先回顾一下KL散度:用来衡量两个分布。如下图公式所示,它表示的在知道p的情况下至少要多少个比特才能够将q描述出来
上式中最终结果中的两项实际上就是两个KL散度如下图中的公式所示
KL散度一定是大于等于零的,KL要等于0,那么p和q要相等
如果C(G)要取得最小值,所以需要两个KL散度等于零,又因为p=q,所以Pdata=(Pdata+Pg)/2,所以C(G)的最优解就等价于Pdata=Pg,这就证明了D在已经取得了最优解的情况下,如果想要对G取最优解的话一定是Pg=Pdata,具体来说,对于写成这种形式的两个分布又叫做JS散度
JS散度和KL散度的区别:JS散度是对称的,而KL不是对称的,不能将p和q进行互换,但是对于JS散度,将p和q进行互换也是可以保持不变的,所以说它是一个对称的散度,而KL是一个不对称的散度
也有评论说因为GAN是一个对称的散度,所以使得它在训练上更加容易。但是也可以取一个更好的目标函数使得训练更加艰难
到此就证明了目标函数的选择还是很不错的
结论二是说算法一是能够优化目标函数的
当G和D有足够的容量的时候而且算法一允许在中间的每一步D是可以达到它的最优解的时候,如果对G的优化是去迭代下图所示的步骤(式中G已经换成最优解了),那么最后的Pg会收敛到Pdata
将目标(价值函数)看成是一个关于Pg(模型或者分布)的函数,Pg其实是一个函数,那么目标函数就是一个关于函数的函数。一个函数的输入可以是标量或者是向量
这里目标函数是一个函数的函数:输入不再是一个值,而是一个值加上了计算(等于是说在python中写一个函数,本来是接收一个x,x是一个vector,然后现在需要接收一个clousure,clousure就包括了计算和数),之前是在高维的值的空间里面做迭代,现在需要在一个函数空间里面做梯度下降
Ex~Pg其实是关于Pg的一个很简单的函数,这个东西展开之后就是把Pg写出来,是一个积分,积分里面有一个Pg(x),后面一项跟Pg无关,所以他其实就是一个线性函数,而且是一个凸函数
在每一步中把D求到最优,就是说一个凸函数的上限函数还是一个凸函数,所以这个凸函数做梯度下降的时候会得到一个最优解
虽然假设了每一次会对D优化到极致,但实际上在算法上只是迭代了k步,所以说这个证明并不能说算法一是工作的,但是实际上算法一跑的还是挺好的(其实算法一跑的并不好,还是挺难收敛的,经常会出现各种问题)
七、实验+总结
 数字生成的还行,但是后面的图片效果不太好,分辨率特别低,需要很长的时间才能生成稍微能看的图片
数字生成的还行,但是后面的图片效果不太好,分辨率特别低,需要很长的时间才能生成稍微能看的图片
总结
坏处是整个训练是比较难的,G和D需要比较好的均衡,如果没有均衡好的话会导致生成的图片比较差
优势是因为生成器并没有看真正样本上的数据,没有试图去拟合真实数据的特征,使得它能够生成一些比较锐利的边缘,但是这个说法在后面发现并不是这样的
八、评价
写作
总的来说,写作还是比较明确的,主要关注GAN在干什么。摘要中主要讲述了GAN在干什么事情。引言非常短,首先写了一点故事性(为什么要做这个事情),然后接下来就是写GAN在干什么。在相关工作中,虽然第一个版本写的比较糟糕,基本上就是在说与别人不一样,但是后来的版本也基本承认了很多想法前面的人工作都已经做过了(真正伟大的工作不在乎你的那些想法在别的地方已经出现过还是没有,关键是说你能够给大家展示用这个东西在某个应用上能够取得非常好的效果,能够让别人信服跟着你继续往下做,然后把整个领域做大,这个是伟大工作的前提)。第三章讲的是GAN的目标函数以及如何做优化。第四章证明了为什么目标函数能得到最优解以及求解算法在一定程度上能够得到最优解。最后一章简单介绍了一些实验和未来的工作。
对于GAN本身这个算法而言
它开创了一个领域,并且影响了之后的很多工作(不仅仅是关于GAN):
1、他是无监督学习的,不需要使用标号;
2、他用一个有监督学习的损失函数来做无监督学习的,他的标号(来自于采样的还是生成的)来自于数据,用了监督学习的损失函数,所以在训练上确实会高效很多,这也是之后自监督学习(比如说BERT)的灵感的来源