机器学习-KNN算法
1、认识KNN算法
K-近邻算法,也叫做KNN算法(K-Nearest Neighbor,KNN),其定义为:如果一个样本在特征空间中的K个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
并且拥有如下的特性:
- 适用于分类问题,尤其是二分类问题,当然也可以用来预测回归问题
- 算法的思想非常的简单易懂,应用的数学知识很少
- 虽然它的算法简单,但是效果很好
2、算法所需要的数学基础
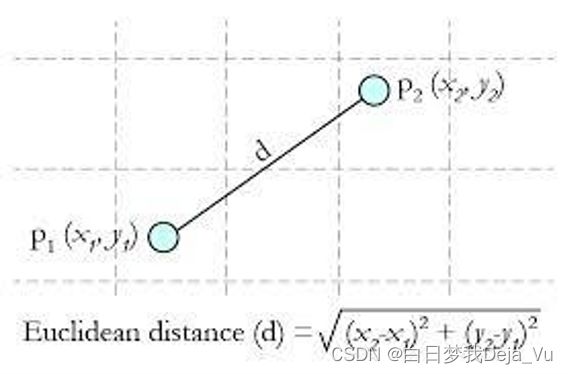
距离公式:
其中,欧式距离也被称为欧几里得距离,例如在二维平面上,两点之间的距离表示如图所示
在多维平面中,欧氏距离表示为
其他距离的衡量还有:余弦值距离(cos), 相关度 (correlation), 曼哈顿距离 (Manhattan distance)
3、KNN例子
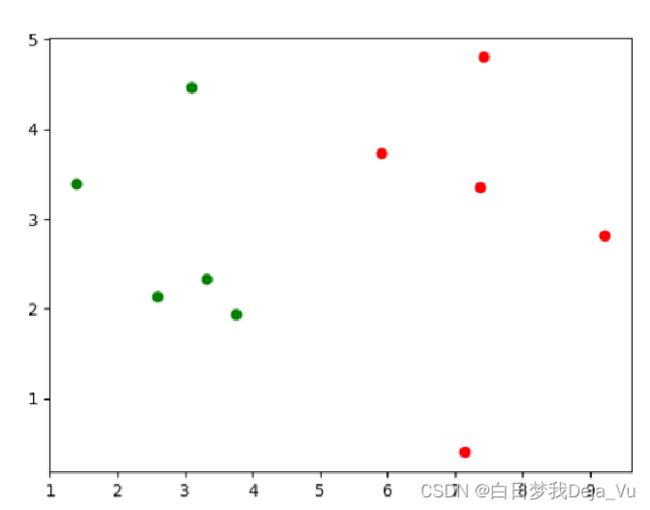
如图所示,在图中有两块区域的点,绿色的点和红色的点,可以将这个图想象成是我们疫情期间的绿码和红码。
这时候出现了一个新的人,我们将他的位置看成是蓝色的点,那么这个人是绿码还是红码呢?
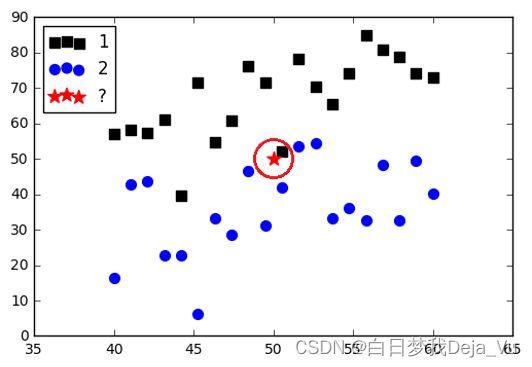
在K近邻算法中,K的意思就是图中我们画的以蓝点为圆心的圈圈中的点的个数,我们可以发现,当我们K值取1的时候,圈里面只有绿点(1个),当我们K值取3的时候,圈里面也只有绿点(3个),根据K近邻算法的算法思想,这个时候我们就可以认为该点(也就是蓝点)属于绿色的阵营里面。
4、KNN算法过程
由刚刚的例子我们也可以总结出来,KNN算法的算法过程如下所示:
1) 确定K的大小和距离计算方法
2) 从训练样本中得到K个与测试最相似的样本
- 计算测试数据与各个训练数据之间的距离
- 按照距离的递增关系进行排序
- 选取距离最小的K个点
- 确定前K个点所在类别的出现频率
- 返回前K个点中出现频率最高的类别作为测试数据的预测分类
3) 根据K个组相似样本的类别,通过少数服从多数的方式来确定测试样本的类别
5、K值的选取
K=1 K=5
K的选取
- K太大的时候,导致分类的影响
- K太小的时候,受个例的影响,波动比较大
如何选取K
- 经验
- 均方根误差
6、算法的缺点
- 算法复杂度较高(需要比较所有已知实例与要分类的实例)
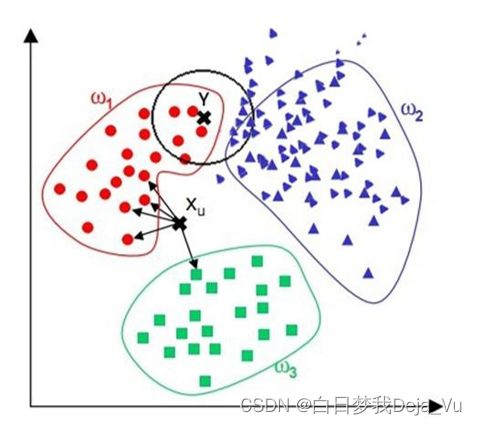
- 当其样本分布不平衡时,比如其中一类样本过大(实例数量 过多)占主导的时候,新的未知实例容易被归类为这个主导样本,因为这类样本实例的数量过大,但这个新的未知实例实际并没有接近目标样本
7、KNN算法的总结
优点:
- 简单有效
- 重新训练的代价低
- 适合类域交叉样本——KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合。
- 适合大样本自动分类——该算法比较适用于样本容量比较大的类域的自动分类,而那些样本容量较小的类域采用这种算法比较容易产生误分。
缺点:
- 惰性学习
- 类别评分不是规格化
- 输出可解释性不强
- 对不均衡的样本不擅长
- 计算量较大
8、代码实例
链接:https://pan.baidu.com/s/1Zq2w-fZivzaDfLDGs8DUxQ?pwd=5jfn
提取码:5jfn
--KNN算法的实例
画图picture.py(本文一开始的绿色和红色图)
import numpy as np
import matplotlib.pyplot as plt
# 定义特征值
raw_data_x = [[3.3144558, 2.33542461],
[3.75497175, 1.93856648],
[1.38327539, 3.38724496],
[3.09203999, 4.47090056],
[2.58593831, 2.13055653],
[7.41206251, 4.80305318],
[5.912852, 3.72918089],
[9.21547627, 2.8132231],
[7.36039738, 3.35043406],
[7.13698009, 0.40130301]]
# 定义目标值
raw_data_y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
X_train = np.array(raw_data_x)
y_train = np.array(raw_data_y)
# 利用matplotlib绘制图像
plt.scatter(X_train[y_train == 0, 0], X_train[y_train == 0, 1], color='g')
plt.scatter(X_train[y_train == 1, 0], X_train[y_train == 1, 1], color='r')
plt.show()
#加入预测点
x = np.array([2.093607318, 2.365731514])
plt.scatter(X_train[y_train == 0, 0], X_train[y_train == 0, 1], color='g')
plt.scatter(X_train[y_train == 1, 0], X_train[y_train == 1, 1], color='r')
plt.scatter(x[0], x[1], color='b')
plt.show()样本集为网盘中的Prostate_Cancer.py
训练test.py
import random
import csv
#读取
with open('Prostate_Cancer.csv','r') as file:
reader = csv.DictReader(file)
datas=[row for row in reader]
# print(datas)
#分组
random.shuffle(datas)
n = len(datas)//3
test_set = datas[0:n]
train_set = datas[n:]
#KNN
def distance(d1,d2):
res = 0
for key in ("radius","texture","perimeter","area","smoothness","compactness","symmetry","fractal_dimension"):
res += (float(d1[key])-float(d2[key]))**2
return res**0.5
K=33
def knn(data):
#1.距离
res = [
{"result":train['diagnosis_result'],"distance":distance(data,train)}
for train in train_set
]
#2.排序-升序
res = sorted(res,key=lambda item:item['distance'])
#3.取前K个
res2 = res[0:K]
#4.加权平均
result = {'B': 0,'M': 0}
#总距离
sum = 0
for r in res2:
sum +=r['distance']
for r in res2:
result[r['result']]+=1-r['distance']/sum
print(result)
print(data['diagnosis_result'])
if result['B']>result['M']:
return 'B'
else:
return 'M'
#测试阶段
correct=0
for test in test_set:
result = test['diagnosis_result'] #真实结果
result2 = knn(test)#测试集结果
if result == result2:
correct+=1
print(f"检测正确的数目:{correct}") #正确的个数
print(f"一共检测的样本数目:{len(test_set)}") #一共的个数
# knn(test_set[0])
print("检测的正确率:{:.2f}%".format(100*correct/len(test_set)))
实验结果
此时取的K值是5,当我们将K值取的过于大或者过于小时,可以发现实验的检测结果变差了。