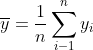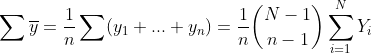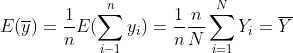抽样技术笔记

1. 调查的基本概念

1.1 普查

是为了某个特定目的专门组织的全面调查。

1.2 抽样调查

是一种非全面调查，按照一定程序从总体中抽选一部分单位进行调查或者观察，对总体参数作出推断的调查方式。有可能获得比普查质量更高的数据质量。抽样调查又可分为概率抽样和非概率抽样。

1.2.1 概率抽样

即随机抽样，按照概率原则，根据“单元是否按照一定的概率入样”划分，总体中每个单位都有一定的概率被选入样本，使得样本对总体具有充分代表性，避免人为因素干扰。

1.2.2 非概率抽样

即非随机抽样，以方便为出发点或者根据研究者主观的判断来抽取样本。依赖研究者个人的经验和判断，无法估计、控制抽样误差，无法用样本来估计总体。

1.2.3 应用领域

调查内容：社会现象调查、经济现象调查，比如收入水平调查、新冠疫情防控调查等等。

调查执行者：市场调查、政府统计调查

1.3 目标总体与抽样总体

1.3.1 目标总体

即总体，指所要研究对象的全体，组成总体的各个个体称作总体单元或者单位。

1.3.2 抽样总体

抽样总体指从总体中抽取样本的总体。

1.4 抽样框与抽样单元

即抽样总体的具体表现，是一份包含所有抽样单元的名单。形式可以是名单、手册、数据包等。

要求：抽样框必须是有序的，即抽样单元必须编号且根据某种顺序进行了排序。抽样框中包含的抽样单元务必要“不重不漏”，否则会出现抽样框误差。

抽样框的数量与抽样单元的层次是相对应的，我们常常会对抽样单元进行分级：

初级单元-->次级单元-->三级单元...-->基本抽样单元

例子：市-->区-->学校-->班级-->学生

1.5 总体参数和（样本）统计量

总体参数：即总体某个特征或者属性的数量表现，如总体总值、总体均值、总体比例、总体比率。

统计量：根据样本的n个单元的变量值计算而出的一个量，也称估计量，是对总体参数的估计。

估计量方差：它从平均的意义上说明了估计值与待估参数的差异状况。可以用此对抽样方案进行评价。

偏差：指按照某一抽样方案反复进行抽样，估计值的数学期望和待估参数之间的离差。无偏估计量偏差为零。

均方误差：Mean Square Error，指所有可能的估计值和待估参数之间离差平方的均值，等于估计量方差假设偏差的平方。

1.6 抽样误差和非抽样误差

抽样误差：是抽样的随机性导致的样本值与总体值之间的差异。随机抽样的抽样误差是可以度量的。

非抽烟误差：是由其他多种原因引起的估计值与总体参数之间的差异，如抽样框误差、计量误差等等。

1.7 精度与费用

精度：是由误差来体现的。通常情况下，样本量越大，在其他条件相同的情况下，抽样误差就越小，抽样调查的精度就越高。

费用：是一个与样本量有关的函数，最简单的是线性费用函数。

最优抽样设计：即用最小的费用（或要求的费用）达到了要求的精度。

1.8 几种基本的抽样方式

1.8.1 概率抽样

简单随机抽样：又称顺随机抽样，从包含N个单位的总体中抽取n个单位作为样本。如果是不放回的情况，则可能有C(N,n)个样本。如果每个样本被抽中的概率相等，则得到的样本叫做简单随机样本（SRS）。

分层抽样：Stratified sampling，又称类别抽样。先将总体分层，在各层中采取简单随机抽样或者系统抽样的方式抽取样本单位。分层时应该使得层间方差尽可能大，层内方差尽可能小。分为等比例抽样和不等比例抽样。

系统抽样：将N个总体单位排序，随机抽取一个单位作为样本第一个单位，然后按照某种确定的规则抽取样本其他单位，最简单的规则是等间隔抽样。排列顺序分成与调查项目有关和无关两种。简单易行，但是抽样误差计算复杂，周期性重合时会影响调查的精确度。

整群抽样：先将总体划分为多个不重合的子总体或者群，再按照某种随机方式抽取若干群，对群内所有单位进行检查。整群抽样没有总体最终单位的抽样框。注意分群时应该使得群内方差尽可能大，群间方差尽可能小。

多阶段抽样：指抽取样本单位时分几个阶段进行。首先在总体中按随机原则抽取若干初级单位，然后从被抽中的初级单位中抽取若干次级单位。若到此为止，称为二阶段抽样，但也可以更多。在大规模抽样调查中，尤其是抽样单位为各行政单位时，常采用这种方法。

1.8.2 非概率抽样

在客观条件限制下无法进行随机抽样，或者为了快速获得调查结果，或者调查对象不确定，或者总体各单位间离散程度不大且调查员有丰富经验时可采用。

判断抽样（典型抽样&重点抽样）：根据研究人员的主观意愿、经验等，从总体中选择具有典型代表性样本作为调查对象。

方便抽样：根据调查者的方便与否来抽取样本，如街头拦人法。

滚雪球抽样：前提是总体单位之间具有一定的联系。

配额度抽样：事先对总体中所有单位按其属性分为若干型，这些属性称作“控制特征”，如年龄等。然后按照各个控制特征分配样本数额。

1.9 抽样调查步骤

（1）确定调研问题

（2）抽样方案步骤

1）抽样调查的目的、任务、要求

2）抽样调查对象的范围和抽样单位

3）抽样方法

4）确定必要样本数

5）对主要抽样指针的精确度提出要求

6）确定总体目标量的估算方法

7）制定实施总体方案的办法和步骤

（3）问卷设计

（4）实施调查过程

（5）数据处理分析（找出异常值、缺失值啊等等）

（6）撰写调查报告

2. 简单随机抽样SRS

2.1 概述

第一章有讲哦。

2.1.1 放回的简单抽样 SRS with replacement

不管从前是否有被抽取中，每次都在N个样本中随机抽取，此时，所有可能的样本为N的平方个（如果考虑样本的顺序），每个样本被抽中的概率相同。注意，由于每次抽样前都会将前一次抽样的单元放回，因此总体结构不变，抽样是相互独立进行的。

样本量不受总体大小的限制（总体一直保持N个），可以是任意的。

2.1.2 不放回的简单抽样

样本量受到总体大小的限制，若非特意说明，简单随机抽样都指不放回的随机抽样。

2.2 样本的抽取

讲容量为N的有限总体所有单元从1到N编号，然后从N个中逐个抽取n个（不可以一次性抽取n个哦）。

具体抽取方法有：

（1）抽签法

（2）随机数表法

（3）通过计算机产生伪随机数（因为计算机的算法始终具有一定规律）

抽取的原则：

（1）按随机原则取样

（2）每个抽样单元被抽中的概率都是已知或事前确定的

（3）每个抽样单元被抽中的概率相等

2.3 简单估计量和性质

注意一下通常的书写方法：总体用大写字母表示，样本用小写字母表示。通常人们只关注四个方面的总体特征，即总体均值、总体总值、总体比例、总体比率。

2.3.1 对总体均值的估计

以样本均值作为总体均值的估计，如下公式：

性质1：对于简单随机抽样， 是 的无偏估计。

证明性质1：对于有限总体，样本估计量的期望即对所有可能的样本求平均值：

总体中每个特定的单元yi在不同样本中出现的次数为

且有

因此

可证。

证明性质1（对称性论证法）：

由于每个单元出现在样本中的次数相同，因此E(y1+y2+...+yn)一定是E(Y1+Y2+...+Yn)的倍数，且这个倍数就是n/N。

因此

可证。

性质2：对于简单随机抽样， 的方差：

式中，f=n/N为抽样比，1-f为有限总体校正系数。