聚类 k-means、yellowbrick和信用卡用户实例 -- 023
微信公众号:python宝
关注可了解更多的python相关知识。若有问题或建议,请公众号留言;
内容目录
一、K-means、畸变程度(SSE)、成本函数、内聚度、分离度、肘部法则和轮廓系数简介二、k-means 介绍和原理1、简介2、K-means算法三、实例信用卡用户聚类1、导入数据和数据显示设置,并查看数据。2、查看是否有重复数据3、删除不必要数据4、观察每个变量的分布5、观察每个变量之间的相关性6、数据处理7、肘部法则应用8、 轮廓系数(Silhouette Coefficient)9、yellowbrick展示结果肘部法则和轮廓系数10、给数据打标签11、绘制打标签后的数据散点图12、部分变量来进行聚类
一、K-means、畸变程度(SSE)、成本函数、内聚度、分离度、肘部法则和轮廓系数简介
K-means:K-means是无监督的聚类算法。其主要思想是选择K个点作为初始聚类中心, 将每个对象分配到最近的中心形成K个簇,重新计算每个簇的中心,重复以上迭代步骤,直到簇不再变化或达到指定迭代次数为止,即让簇内的点尽量紧密的连接在一起,而让簇间的距离尽量的大。
畸变程度(即SSE簇内误方差;):每个簇的质点与簇内样本点的平方距离误差和称为畸变程度(distortions)。对于一个簇,畸变程度越低,代表簇内成员越紧密;畸变程度越高,代表簇内结构越松散。畸变程度会随着类别的增加而降低,但对于有一定区分度的数据,在达到某个临界点时畸变程度会得到极大改善,之后缓慢下降,这个临界点就可以考虑为聚类性能较好的点;
成本函数:成本函数为各个类畸变程度SSE之和;
肘部法则:肘部法则是通过成本函数来刻画的,其是通过将不同K值的成本函数刻画出来,随着K值的增大,平均畸变程度会不断减小且每个类包含的样本数会减少,于是样本离其重心会更近。但是,随着值继续增大,平均畸变程度的改善效果会不断减低。因此找出在K值增大的过程中,畸变程度下降幅度最大的位置所对应的K较为合理。
内聚度:簇内不相似度。针对样本空间中的一个特定样本i,计算 a(i) = average(i向量到所有它属于的簇中其它点的距离);
分离度:针对样本空间中的一个特定样本i, b(i) = min (i向量到所有非本身所在簇的点的平均距离) ;
轮廓系数:轮廓系数(Silhouette Coefficient),是聚类效果好坏的一种评价方式。针对样本空间中的一个特定样本,计算它与所在聚类其它样本的平均距离a,以及该样本与距离最近的另一个聚类中所有样本的平均距离b,该样本的轮廓系数为(b-a)/max(a, b),将整个样本空间中所有样本的轮廓系数取算数平均值,作为聚类划分的性能指标s。轮廓系数的值是介于 [-1,1] ,越趋近于1代表内聚度和分离度都相对较优。最后将所有样本点的轮廓系数求平均,就是该聚类结果总的轮廓系数。
二、k-means 介绍和原理
1、简介
聚类的目的也是把数据分类,但是事先我是不知道如何去分的,完全是算法自己来判断各条数据之间的相似性,相似的就放在一起。在聚类的结论出来之前,我完全不知道每一类有什么特点,一定要根据聚类的结果通过人的经验来分析,看看聚成的这一类大概有什么特点。
聚类和分类最大的不同在于:分类的目标是事先已知的,而聚类则不一样,聚类事先不知道目标变量是什么,类别没有像分类那样被预先定义出来。
KMeans(
n_clusters=8,
init='k-means++',
n_init=10,
max_iter=300,
tol=0.0001,
precompute_distances='auto',
verbose=0,
random_state=None,
copy_x=True,
n_jobs=None,
algorithm='auto',
)
参数:
n_clusters:整形,缺省值=8 【生成的聚类数,即产生的质心(centroids)数。】
max_iter:整形,缺省值=300 ,执行一次k-means算法所进行的最大迭代数。
n_init:整形,缺省值=10 ,用不同的质心初始化值运行算法的次数,最终解是在inertia意义下选出的最优结果。
init:有三个可选值:’k-means++’, ‘random’,或者传递一个ndarray向量。
此参数指定初始化方法,默认值为 ‘k-means++’。
(1)‘k-means++’ 用一种特殊的方法选定初始质心从而能加速迭代过程的收敛(即上文中的k-means++介绍)
(2)‘random’ 随机从训练数据中选取初始质心。
(3)如果传递的是一个ndarray,则应该形如 (n_clusters, n_features) 并给出初始质心。
precompute_distances:三个可选值,‘auto’,True 或者 False。
预计算距离,计算速度更快但占用更多内存。
(1)‘auto’:如果 样本数乘以聚类数大于 12million 的话则不预计算距离。This corresponds to about 100MB overhead per job using double precision.
(2)True:总是预先计算距离。
(3)False:永远不预先计算距离。
tol:float形,默认值= 1e-4 与inertia结合来确定收敛条件。
n_jobs:整形数。 指定计算所用的进程数。内部原理是同时进行n_init指定次数的计算。
(1)若值为 -1,则用所有的CPU进行运算。若值为1,则不进行并行运算,这样的话方便调试。
(2)若值小于-1,则用到的CPU数为(n_cpus + 1 + n_jobs)。因此如果 n_jobs值为-2,则用到的CPU数为总CPU数减1。
random_state:整形或 numpy.RandomState 类型,可选;
用于初始化质心的生成器(generator)。如果值为一个整数,则确定一个seed。此参数默认值为numpy的随机数生成器。
copy_x:布尔型,默认值=True
当我们precomputing distances时,将数据中心化会得到更准确的结果。如果把此参数值设为True,则原始数据不会被改变。如果是False,则会直接在原始数据 上做修改并在函数返回值时将其还原。但是在计算过程中由于有对数据均值的加减运算,所以数据返回后,原始数据和计算前可能会有细小差别。
属性:
cluster_centers_:向量,n_clusters, n_features
Labels_: 每个点的分类
inertia_:float形 ,每个点到其簇的质心的距离之和。
Methods:
fit(X[,y]): 计算k-means聚类。
fit_predictt(X[,y]): 计算簇质心并给每个样本预测类别。
fit_transform(X[,y]):计算簇并 transform X to cluster-distance space。
get_params([deep]):取得估计器的参数。
predict(X):predict(X) 给每个样本估计最接近的簇。
score(X[,y]): 计算聚类误差
set_params(params): 为这个估计器手动设定参数。
transform(X[,y]): 将X转换为群集距离空间。在新空间中,每个维度都是到集群中心的距离。请注意,即使X是稀疏的,转换返回的数组通常也是密集的。
2、K-means算法
K-means算法的过程
首先输入k的值,即我们希望将数据集经过聚类得到k个分组;
从数据集中随机选择k个数据点作为初始质心(质心,Centroid);
对集合中每一个对象,计算与每一个初始质心的距离,离哪个质心距离近,就属于哪个质心簇;
这时,每个质心簇都有很多对象,此时需要通过算法重新选出新的质心
如果新大哥和老大哥之间的距离小于某一个设置的阈值(表示重新计算的质心的位置变化不大,趋于稳定,或者说收敛),可以认为我们进行的聚类已经达到期望的结果,算法终止。
如果新大哥和老大哥距离变化很大,需要迭代3~5步骤。
三、实例信用卡用户聚类
1、导入数据和数据显示设置,并查看数据。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import warnings
import seaborn as sns
warnings.filterwarnings('ignore')#忽略各种报红警告
pd.set_option('display.max_columns', None)#显示所有列
pd.set_option('display.max_rows', None)#显示所有行
#设置value的显示长度为100,默认为50
pd.set_option('max_colwidth',100)
pd.set_option('display.width', 5000) #dataframe不换行
# k-means无监督的机器学习算法
df = pd.read_csv('D:\A\AI-master\py-data\CreditCardUsage.csv')
df.head()
df.shape#(8950, 18)
df.describe().T2、查看是否有重复数据
print("Number of unique id's in CUST_ID column : ",df.CUST_ID.nunique())
print("Number of rows in dataframe : ",df.shape[0])
3、删除不必要数据
df.drop(columns='CUST_ID',inplace=True)
4、观察每个变量的分布
f = plt.figure(figsize=(20,20))
for i ,col in enumerate(df.columns):
ax = f.add_subplot(6,3,i+1)
sns.distplot(df[col].ffill(),kde=False)
ax.set_title(col+'discribution',color = 'blue')
plt.ylabel('discribution')
plt.show()
f.tight_layout()
'''
tight_layout会自动调整子图参数,使之填充整个图像区域。这是个实验特性,
可能在一些情况下不工作。它仅仅检查坐标轴标签、刻度标签以及标题的部分。
'''
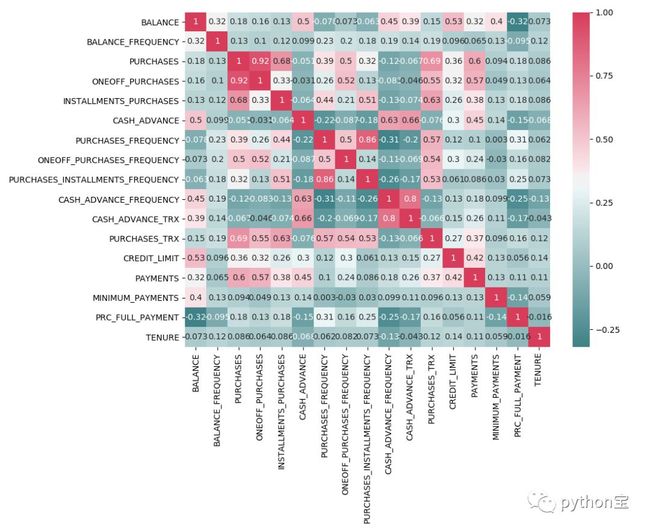
5、观察每个变量之间的相关性
corr = df.corr()
f, ax = plt.subplots(figsize=(11, 9))
cmap = sns.diverging_palette(200, 5, as_cmap=True)
sns.heatmap(corr, annot=True,cmap=cmap)
plt.show()
6、数据处理
首先填补数据中的空缺值。
print('Check the null values for all columns:\n', df.isna().sum())
df["CREDIT_LIMIT"].fillna(df["CREDIT_LIMIT"].median(), inplace=True)
df['MINIMUM_PAYMENTS'].fillna(df['MINIMUM_PAYMENTS'].median(), inplace=True)
然后将数据进行标准化。需要标准化的原因是K-Means基于样本点的空间距离来进行划分。
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler_df = scaler.fit_transform(df)
type(scaler_df)#numpy.ndarray
df_scaled = pd.DataFrame(scaler_df, columns=df.columns)
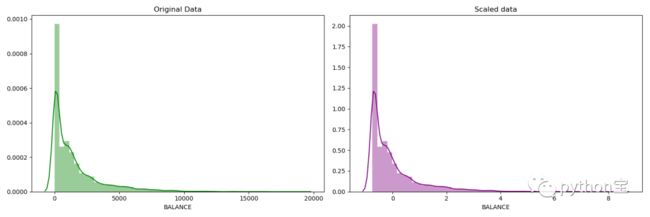
展示标准化前后数据的分布是否有区别?
fig, ax=plt.subplots(1,2,figsize=(15,5))
sns.distplot(df['BALANCE'], ax=ax[0],color='green')
ax[0].set_title("Original Data")
sns.distplot(df_scaled['BALANCE'], ax=ax[1],color='purple')
ax[1].set_title("Scaled data")
plt.show()
f.tight_layout()
7、肘部法则应用
首先尝试通过Elbow曲线来找到最优的K。Elbow描述了每个点到其中心的距离的平方之和。我们希望找到K是的Elbow尽可能的小。
from sklearn.cluster import KMeans
Sum_of_squared_distances = []
K = range(1,21)
for k in K:
km = KMeans(n_clusters=k)
km = km.fit(df_scaled)
Sum_of_squared_distances.append(km.inertia_)#inertia簇内误差平方和
print('Sum_of_squared_distances',Sum_of_squared_distances)
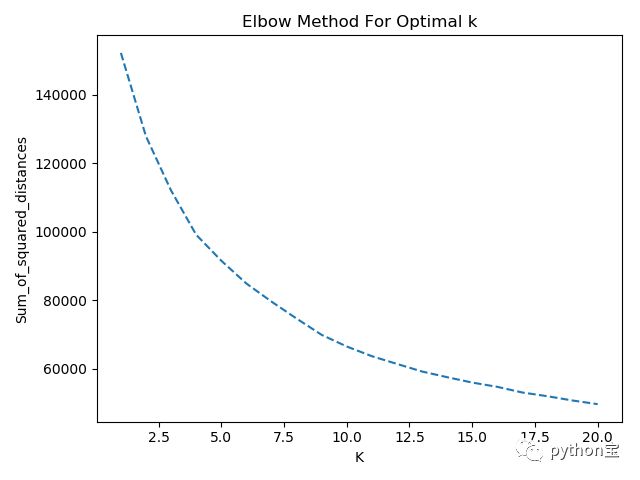
plt.plot(K,Sum_of_squared_distances,'--')
plt.xlabel('K')
plt.ylabel('Sum_of_squared_distances')
plt.title('Elbow Method For Optimal k')
plt.show()
#inertias:是K-Means模型对象的属性,它作为没有真实分类结果标签下的非监督式评估指标。表示样本到最近的聚类中心的距离总和。值越小越好,越小表示样本在类间的分布越集中。
从上图中,我们发现随着K的增加,Elbow减小,所以不能通过这个来找到相对优的K。
8、 轮廓系数(Silhouette Coefficient)
轮廓系数(Silhouette Coefficient),是聚类效果好坏的一种评价方式。它结合内聚度和分离度两种因素。可以用来在相同原始数据的基础上用来评价不同算法、或者算法不同运行方式对聚类结果所产生的影响。
from sklearn.metrics import silhouette_score, silhouette_samples
for n_clusters in range(2,21):
km = KMeans (n_clusters=n_clusters)
preds = km.fit_predict(df_scaled)
centers = km.cluster_centers_
score = silhouette_score(df_scaled, preds, metric='euclidean')
print ("For n_clusters = {}, silhouette score is {}".format(n_clusters, score))
For n_clusters = 2, silhouette score is 0.21004188358425524
For n_clusters = 3, silhouette score is 0.2505645588142349
For n_clusters = 4, silhouette score is 0.1976791965228765
For n_clusters = 5, silhouette score is 0.19331998004017914
For n_clusters = 6, silhouette score is 0.20269576868001302
For n_clusters = 7, silhouette score is 0.2151983315275981
For n_clusters = 8, silhouette score is 0.22193282658122515
For n_clusters = 9, silhouette score is 0.22597171325679777
For n_clusters = 10, silhouette score is 0.22377163432486205
For n_clusters = 11, silhouette score is 0.21839970070970552
For n_clusters = 12, silhouette score is 0.21647080732380802
For n_clusters = 13, silhouette score is 0.21894222923234266
For n_clusters = 14, silhouette score is 0.1954222102915328
For n_clusters = 15, silhouette score is 0.20252680972070905
For n_clusters = 16, silhouette score is 0.2014870019616158
For n_clusters = 17, silhouette score is 0.20688222974140555
For n_clusters = 18, silhouette score is 0.19998121764304877
For n_clusters = 19, silhouette score is 0.1986358047419112
For n_clusters = 20, silhouette score is 0.20992591354578377
发现,n=3的时候,silhouette score最大。
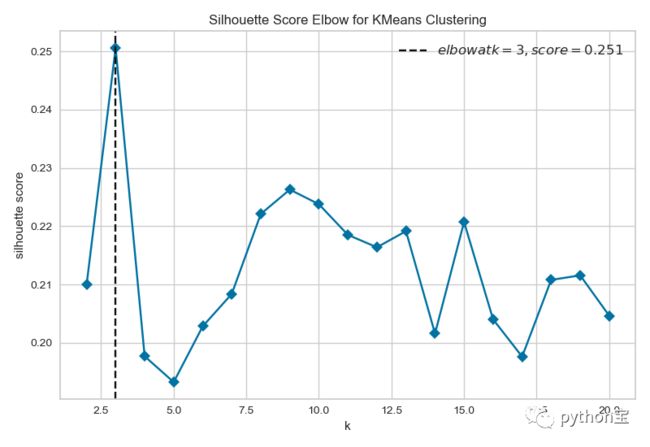
9、yellowbrick展示结果肘部法则和轮廓系数
肘部法则
from yellowbrick.cluster import KElbowVisualizer
km = KMeans(n_clusters=3)
visualizer = KElbowVisualizer(km,k = (2,21),metric='silhouette',timings=False)
visualizer.fit(df_scaled)
visualizer.poof()
轮廓系数
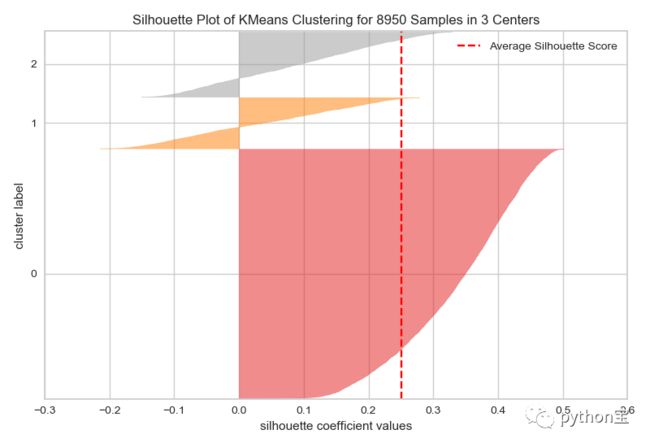
from yellowbrick.cluster import SilhouetteVisualizer
# 该系数计算为每个样本的平均簇内距离和平均最近簇距离之间的差异,并由最大值归一化。
# 这会产生一个介于-1和+1之间的分数,其中+1附近的分数表示高分离度,
# 而-1附近的分数表示样本可能被分配到了错误的簇。
# 每个轮廓的宽度与分配给集群的样本数成比例。
km = KMeans(n_clusters=3)
visualizer = SilhouetteVisualizer(km)
visualizer.fit(df_scaled)
visualizer.poof()
结论:发现,n=3的时候,silhouette score最大。但是我们发现,在n等于3的时候,对于0这组,所有的点的轮廓系数都大于0,说明聚类的很好,但是对于1和2这两组,有大量小于0的点,说明聚类的情况不佳。
10、给数据打标签
数据打标签。
km = KMeans(n_clusters=3)
km.fit(df_scaled)
cluster_label = km.labels_
df_scaled['KMeans_Labels'] = cluster_label
df_scaled.head()
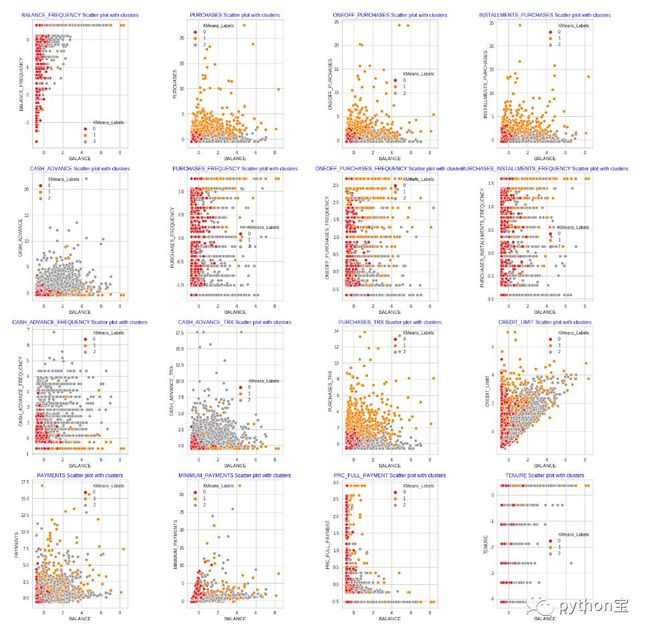
11、绘制打标签后的数据散点图
f=plt.figure(figsize=(20,20))
scatter_cols =['BALANCE_FREQUENCY', 'PURCHASES', 'ONEOFF_PURCHASES',
'INSTALLMENTS_PURCHASES', 'CASH_ADVANCE', 'PURCHASES_FREQUENCY',
'ONEOFF_PURCHASES_FREQUENCY', 'PURCHASES_INSTALLMENTS_FREQUENCY',
'CASH_ADVANCE_FREQUENCY', 'CASH_ADVANCE_TRX', 'PURCHASES_TRX',
'CREDIT_LIMIT', 'PAYMENTS', 'MINIMUM_PAYMENTS', 'PRC_FULL_PAYMENT',
'TENURE']
for i, col in enumerate(scatter_cols):
ax=f.add_subplot(4,4,i+1)
sns.scatterplot(x=df_scaled['BALANCE'],y=df_scaled[col],hue=df_scaled['KMeans_Labels'],palette='Set1')
ax.set_title(col+" Scatter plot with clusters",color='blue')
plt.ylabel(col)
f.tight_layout()
从图中可以看出效果不是很好,对于n=3,结果依旧不令人满意;
12、部分变量来进行聚类
sample_df = pd.DataFrame([df['BALANCE'],df['PURCHASES']])
sample_df = sample_df.T
sample_df.head()
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
Sample_Scaled_df = scaler.fit_transform(sample_df)
km_sample = KMeans(n_clusters=4)
km_sample.fit(Sample_Scaled_df)
sample_df['label'] = km_sample.labels_
sns.set_palette('Set2')
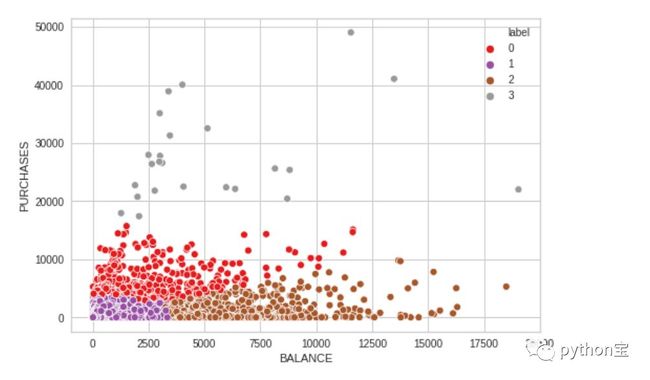
sns.scatterplot(sample_df['BALANCE'],sample_df['PURCHASES'],hue=sample_df['label'],palette='Set1')
从上图可以看出使用部分数据时可以看到较为清晰的结果,并且可以对他们进行分组。
About Me:小婷儿
● 本文作者:小婷儿,专注于python、数据分析、数据挖掘、机器学习相关技术,也注重技术的运用
● 作者博客地址:https://blog.csdn.net/u010986753
● 本系列题目来源于作者的学习笔记,部分整理自网络,若有侵权或不当之处还请谅解
● 版权所有,欢迎分享本文,转载请保留出处
● 微信:tinghai87605025 联系我加微信群
● QQ:87605025
● QQ交流群py_data :483766429
● 公众号:python宝 或 DB宝
● 提供 OCP、OCM 和高可用最实用的技能培训
● 题目解答若有不当之处,还望各位朋友批评指正,共同进步
![]()
如果你觉得到文章对您有帮助,欢迎赞赏,有您的支持,小婷儿一定会越来越好!