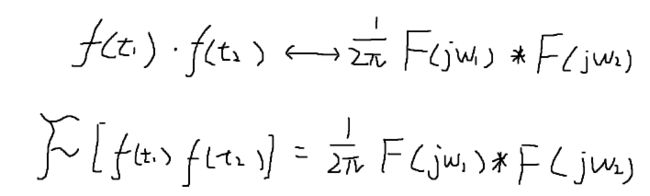现代计算机图形学入门-L6-光栅化.2
光栅化2(Rasterization)--反走样(Antialiasing)
1. 走样问题的引入(Antialiasing)
1.1 问题
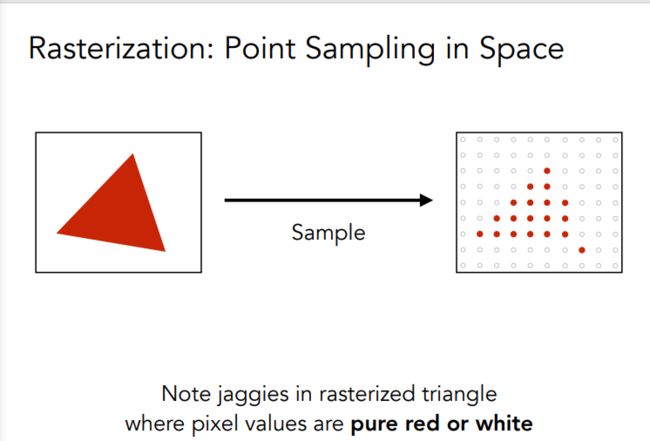
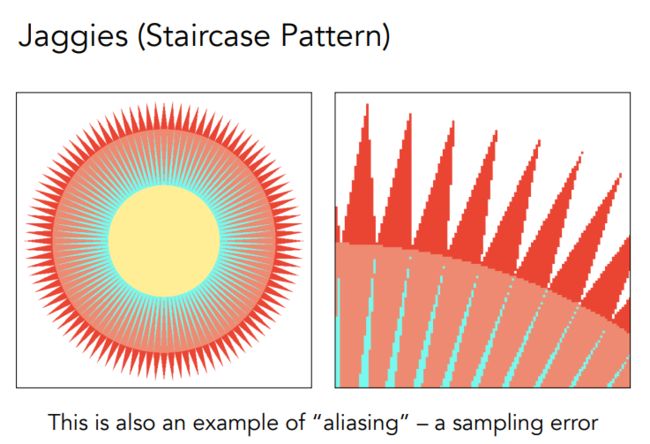
- 表现(看到的内容):Jaggies(锯齿)
- 锯齿学名:Aliasing(走样)
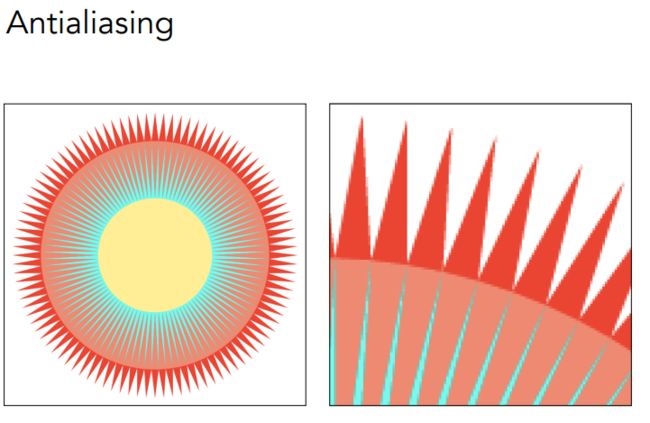
- 反走样(Antialiasing) 目标表现
2.采样(Sample)理论
空间上采样

时间上采样

3.采样带来的问题——Sampling Artifacts(失真)
失真情况(什么是走样):
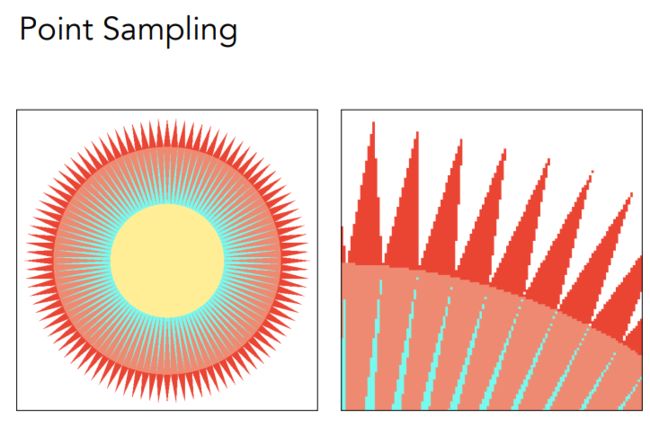
- Jaggies 锯齿
- Moire' Patterns in Image 摩尔纹

- Wagon wheel effect-sample time 车轮效应
 有些条纹显得在逆时针旋转,在生活 中我们也经常能看到类似的现象,比 如高速行驶的汽车,其轮子看上去在 反向旋转,这是因为人眼在时间中的 采样速度更不上运动的速度造成的。
有些条纹显得在逆时针旋转,在生活 中我们也经常能看到类似的现象,比 如高速行驶的汽车,其轮子看上去在 反向旋转,这是因为人眼在时间中的 采样速度更不上运动的速度造成的。 - more ...
「问题的本质原因:采样的速度跟不上信号变换的速度。」

4. 走样的解决办法
- 1.采样前先对原始的信号进行模糊/滤波
- 2.再对处理过的进行采样。
「上面两步顺序不可调转」
5 为什么可以采取上述的解决办法处理走样问题?
为了深入了解上述应用方法的原理,我们需要了解「频域」方面的知识。
这里羽毛建议先预读以下资料,否则后续的内容较难理解。
5.1 前置拓展阅读内容
「1. H264系列五 图像与滤波」 https://www.jianshu.com/p/03c51c8debf4 「2. H264系列六 傅里叶变换」 https://www.jianshu.com/p/bc006222ba64
5.1.1 Frequency(频率)
频率(frequency)是波动快慢的指标,单位时间内波动次数越多,频率越高,反之越低。
5.1.2 时域(时间域)(time domain)
自变量是时间,即横轴是时间,纵轴是信号的变化。其动态信号x(t)是描述信号在不同时刻取值的函数。 在时域图中,横轴是时间,纵轴是振幅。时域图显示振幅随时间的变化。
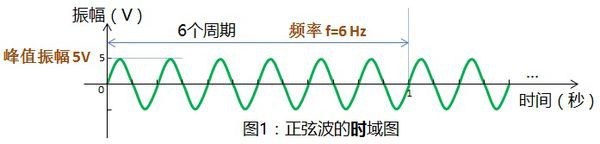 图1
图1
5.1.3 频域(频率域)(frequency domain)
图2是图1中正弦波的频域图,「在频域图中,横轴是频率,纵轴是峰值振幅,峰值振幅,峰值振幅」。频域图仅仅示出峰值振幅与频率,而不显示振幅随时间的变化。
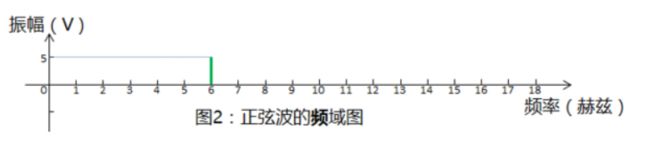 图2
图2
从频域图可以看出,正弦波的频率为6Hz,这个6Hz的正弦波的峰值振幅为5
频域图的优点是,从频域图中,可以一眼看出正弦波的频率和峰值振幅。 「整个正弦波在频域图上只是一个立柱(因为图一的正弦波只有一个频率)」,立柱的位置显示了正弦波的频率,立柱的高度显示了正弦波的峰值振幅。
5.1.4 时域与频域的关系(frequency domain)
动态信号从时间域变换到频率域主要通过傅立叶级数和傅立叶变换实现。周期信号靠傅立叶级数,非周期信号靠傅立叶变换。时域越宽,频域越窄。
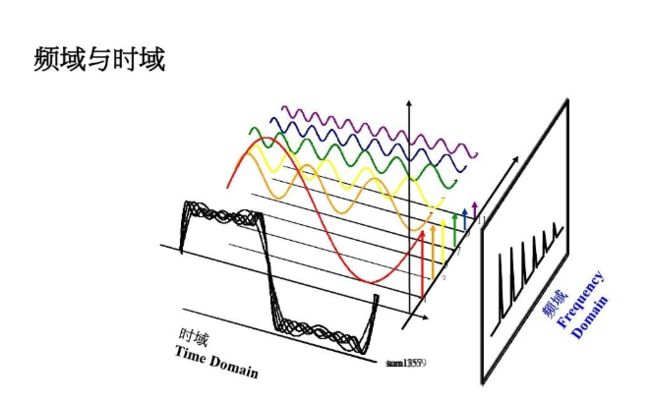

5.2 傅里叶级数展开
任何一个周期函数,可以使用一个Sin/Cos的线性组合以及一个常数项表示
 左侧的每一段周期函数都是一个展开项,组合后共同表示右侧信号
左侧的每一段周期函数都是一个展开项,组合后共同表示右侧信号  注意上图左边不同数量的小圆圈——不同的傅里叶级数
注意上图左边不同数量的小圆圈——不同的傅里叶级数
box函数是所需要描述的周期函数,随着余弦项的增加,傅里叶级数展开的结果f(x)越来越接近box函数。
通过展开,任何一个函数都可以分解成不同的频率表示。
 傅里叶变换和这幅图中的变换非常类似,只不过基函数不是一颗像素,而是震荡的三角函数
傅里叶变换和这幅图中的变换非常类似,只不过基函数不是一颗像素,而是震荡的三角函数
5.3 Fourier Transform(傅里叶变换)
 xy轴时域,
xy轴时域,
- 傅里叶变换:将函数变换为频率表示,对于周期函数,再进行傅里叶级数展开(例:box->f(x)),对于非周期函数,变换为频域分布图(如图5.3)。
- 「作用:时域信号转换为频域信号——把函数变成不同的频率的段,并显示出来」
- 逆傅里叶变换:对傅里叶展开式求积,还原原信号。(例:f(x)->box)
- 频域信号转换为时域信号
- 作用举例
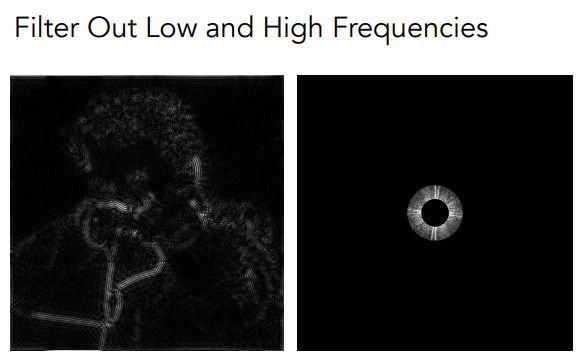
 图5.3,原始图像中含有噪声,因为噪声往往是细小的雪花点,属于图像高频分量,因此我们把图像首先做傅里叶变换,得到右图,然后把变换后的三角函数前的系数中属于高频的部分全部去掉(置0),然后再做逆傅里叶变换,,我们发现图像中的细节(噪声点)减少了。
图5.3,原始图像中含有噪声,因为噪声往往是细小的雪花点,属于图像高频分量,因此我们把图像首先做傅里叶变换,得到右图,然后把变换后的三角函数前的系数中属于高频的部分全部去掉(置0),然后再做逆傅里叶变换,,我们发现图像中的细节(噪声点)减少了。
5.4 走样(通过频率分析)
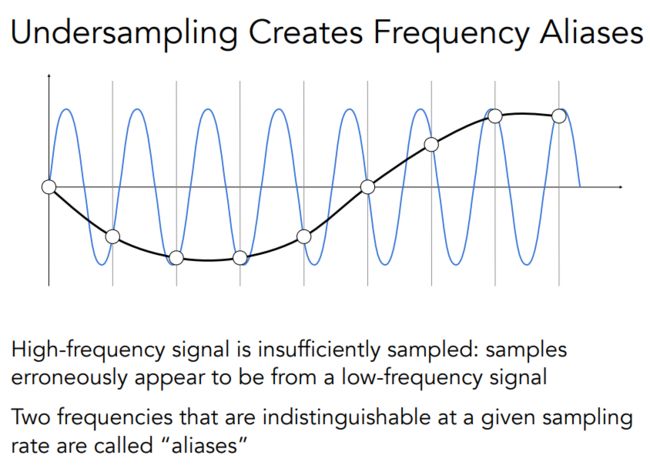
 如上图,随着原始信号的频率增大,采样频率不变,采样频率跟不上原始信号的辩频率,采样得到的函数逐渐偏离原始信号。
如上图,随着原始信号的频率增大,采样频率不变,采样频率跟不上原始信号的辩频率,采样得到的函数逐渐偏离原始信号。
「走样的正规定义:通过同样的采样方法,对两个频率不同的信号进行采样,得到的信号无法区分。(如下图)」
5.5 滤波
-
「图像的本质是波」
如果把任意图像的任意一行像素,取这行像素的R\G\B值,以这一行像素的位置为x轴,可得下图:
 时域信号
时域信号
可以看到,每条曲线在不同的区域波动的大小,有些区域平缓,有些区域急剧变化——变换快慢可以用“频率”来描述(中学知识)。
「因此,图像的本质是波,是各种色彩波的叠加。」
-
傅里叶变换作用:在原信号每一处求其变换频率,把函数从时域变成频域,并用不同的频率表示(如下右侧图)。
-
图像不带任何时间的信息,但在空间上的位置也算作时域,这只是一个名字。
-
经过傅里叶变换后,可以观察到不同频率的信号的分布——频谱
-
色彩变化剧烈的就是图像的高频区域,
-
色彩稳定平滑的地方,就是低频区域

「时域-->频域,中心频率最低(单位周期内信号变换程度),周围为高频区域,中心到周围频率越来越高,亮度表示在不同频率的位置上,有多少信息」
-
-
「滤波器」
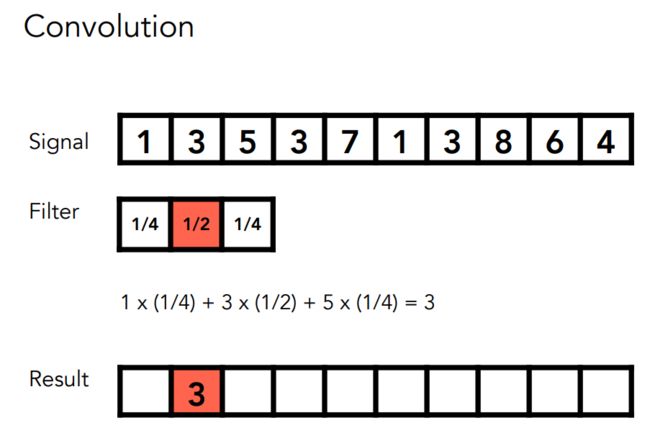
5.6 卷积
-
卷积操作
-
卷积定理
通过卷积定理,我们可以通过两种办法做一个卷积
-
- 拿到一幅图,直接拿一个滤波器做一个卷积操作,
-
- 也可以将这幅图先傅里叶变换到频域上,把滤波器也变换到频域上,把两者相乘,然后再通过逆傅里叶变换到时域上,也完成了一个卷积操作。

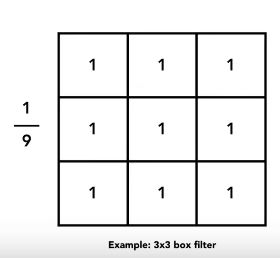 box滤波器——低通滤波器
box滤波器——低通滤波器
时域盒子变大,留下更低的频率————对更大的范围取平均(更加模糊)

频域上表现也一致,频域上乘积后,表现为越来越倾向低频。
采用极限法也可以理解:
- 对每一个像素,用极小的滤波器进行性滤波,例如只有一个像素,相当于不滤波。
- 对每一个像素,用极大的滤波器,例如整张图,平均的更严重,变现更模糊。
5.7从频率的视角看采样
采样:其实就是重复频域上的内容 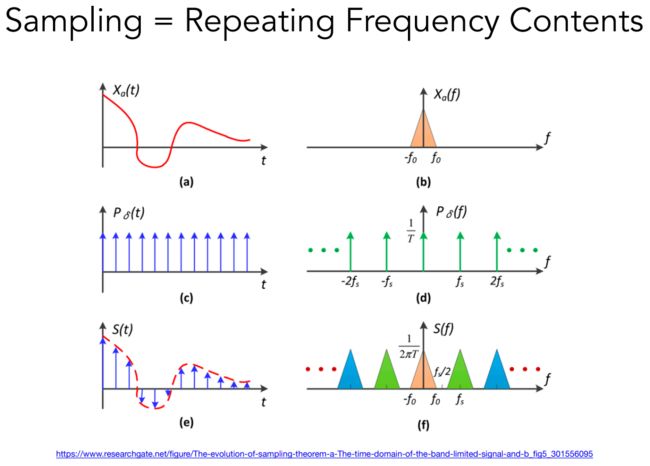 原始函数(a)与冲激函数(c)乘积,得到一系列离散的点(e)
原始函数(a)与冲激函数(c)乘积,得到一系列离散的点(e)
由频域卷积定理,原始函数(a)与冲激函数(c)乘积,等于a、c的频谱b、d的卷积乘以1/2π,结果为f
其实在频域上做的操作就是把原始的函数,它的频谱给复制粘贴了很多份。
「采样,就是重复原始信号的频谱。因此可以解释为什么会产生走样现象。」
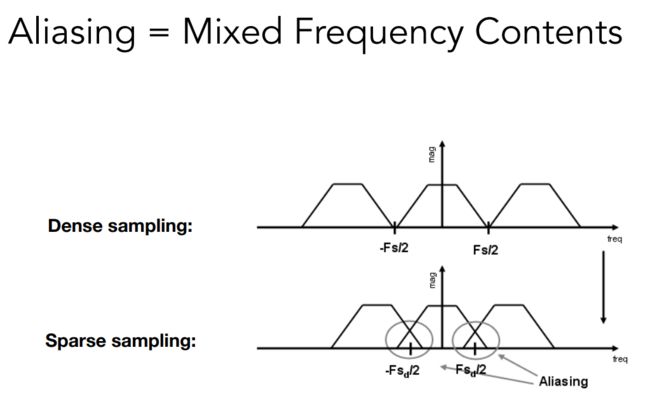
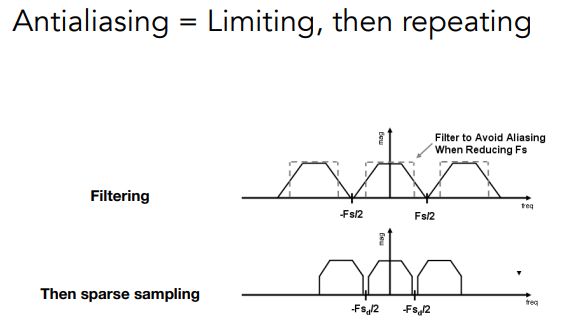
如果采样率不足,或者说采样得不够快,那么复制粘贴的间隔就会非常小,原始的信号和复制粘贴的信号混叠在一块,在这种情况下,就发生了走样。「如果在采样前先进行低通滤波,就没有重叠了。」
6 如何进行反走样
6.1 增加采样率
 受物理限制,不是反走样的可选做法。比如不可以增加屏幕分辨率。
受物理限制,不是反走样的可选做法。比如不可以增加屏幕分辨率。
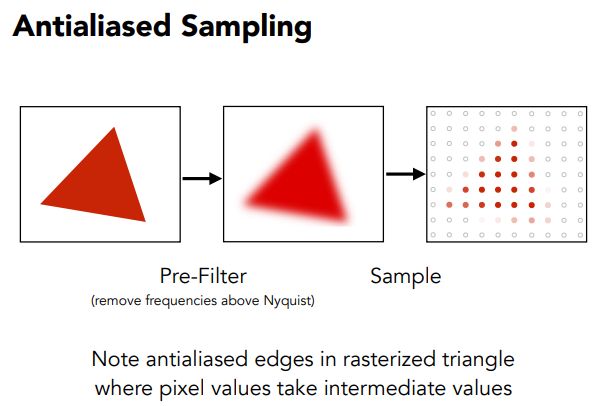
6.2 低通滤波
先过滤掉高频信息(低通滤波),再采样

6.3 如何做模糊——低通滤波器
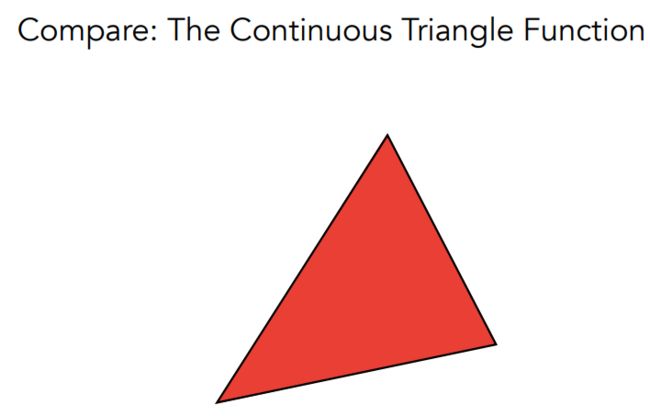
对每一个像素,对三角形覆盖面积求平均
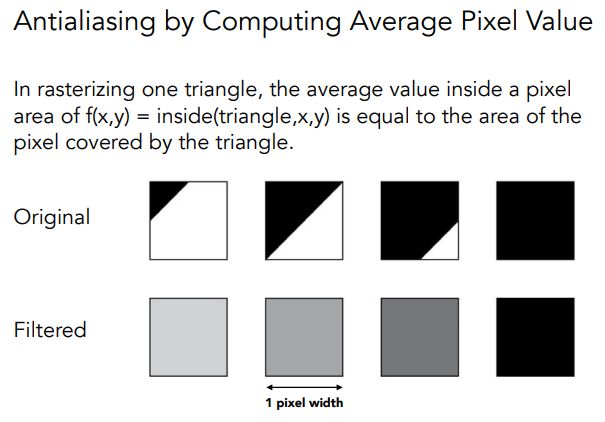
Supersampling MSAA
实际操作,采用近似方法。把一个像素A拆分为多个小的像素,对每一个小的像素中心判断是否在三角形内,最后把这些小像素的结果求平均,作为像素A的结果。

 拆分前
拆分前  拆分后,求平均
拆分后,求平均  结果
结果 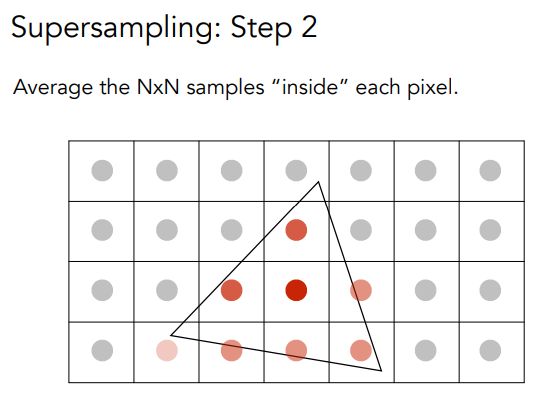 其他点类似
其他点类似 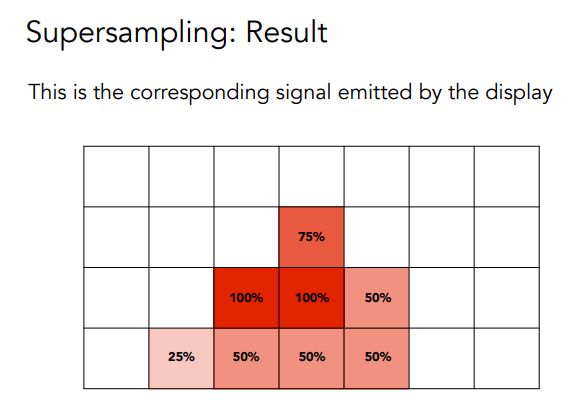
「代价:」
增加计算量。增加的计算量取决于对一个像素的划分粒度。比如 2 * 2 就是 4 倍的计算量;4 * 4 就是 16 倍的计算量。 但是实际的工业应用中,为了减少计算量,不会用这么规则的划分成比如说 4 * 4 个点,会采取一些更加有效的图案来分布这些不同的点,并且有一些点还会被临近的像素所复用。
FXAA(Fast Approimate AA)
图像的后期处理,先得到有锯齿的图,通过图像匹配的方式找到这些边界,并且把这些边界换成没有锯齿的边界,速度非常快,与采样无关的方法,效果也挺不错。
TAA(Temporal AA)
- Temporal 表示和时间相关的
- 对于静止物体,相邻两帧显示的内容相同。复用上一帧感知到的结果。本质上就是把MSAA的样本分布在时间,
7 Super resolution 超分辨率
本质跟抗锯齿一样。都是解决样本不足的问题。
比如一张 512 * 512 的图,把它拉大成 1024 * 1024 的图,那看到的全是锯齿。想把这张图拉大,但我又不想看到锯齿,这就跟抗锯齿很相似。
- DLSS 深度学习的方法,图片拉大后有些细节缺失,使用深度学习的方式对确实细节进行猜测。深度学习非常擅长目前一切涉及猜测的技术。
总结
本节课程首先通过锯齿问题引入了走样问题。为了解释走样原因以及走样的解决办法(反走样)
- 首先,从采样的理论开始介绍,采样可以在空间和时间上及进行,采样存在失真(Artifact)问题,问题的本质原因是采样的速度跟不上信号变换的速度——图像在屏幕上是离散的像素(采样过程),实际图形是连续的图形(原始信号,边界变化快)。
- 然后以锯齿问题为例,提出失真的解决办法是先模糊(实际上就是做低通滤波)再采样,于是锯齿问题得到了很大的改善。
- 接下来解释为什么可以采取先模糊再采样的方式处理失真情况。
- 首先需要了解时域、频域、傅里叶级数、傅里叶变换、卷积与滤波等概念。
- 了解概念后,从频域的角度理解走样,走样的正规定义——通过同样的采样方法,对两个频率不同的信号进行采样,得到的信号发生重叠,无法区分。
- 图像的本质是波,经过低通滤波后,可以解决重叠问题,从而解决走样问题。
- 在图形学中中做低通滤波,其实就是在做平均,对每个像素在三角形内的面积平均到整个像素。实际操作中是使用MSAA方式进行,把单个像素划分为多个小像素后,求小像素在三角形内的个数后,进行平均。 但是实际的工业应用中,为了减少计算量,还会采取一些更加有效的图案来分布这些不同的点,并且有一些点还会被临近的像素所复用。以及后期发展出FXAA(后期处理,与采样无关)与TAA(样本在时间上分布)等方式。
福利
关注公众号“羽毛不会飞”,后台回复“计算机图形学”,获得虎书第二版中文版,虎书第四版英文版,games101课件
恰饭区
「点点广告也是爱,攒攒明年植发钱。」
更多
现代计算机图形学入门-L5-光栅化.1-视口变换与光栅化过程
现代计算机图形学入门-L4-变换.2
现代计算机图形学入门-L3-变换.1
现代计算机图形学入门-L2 ——线性代数
现代计算机图形学入门-L1
另辟蹊径的"一键打包"
Web/Native资源加密方案
Spine换装方案多平台解析
基于creator3.0的3D换装
CocosCreator3.4.2原生二次开发的正确姿势——手把手教你接SDK
在编辑器上声明自定义数据数组
包体优化指南
不规则3D地形行走
快速实现3d抛物线绘制
奇形怪状-不规则按钮实现
关于作者
我是羽毛,一名游戏研发工程师,一名野生摄影同学。我的公众号主要分享自己的一些游戏项目开发过程中的功能总结及日常开发笔记。也希望能通过平台的交流,与更多有想法的同学交流认识,共同成长。
欢迎大家在日常开发过程中,如果觉得有需要讨论解决、分享或者探讨的内容,在公众号后台或者文章留言处给我反馈,提供写作的方向,从另一个角度也尽量让写作内容更贴近大家的需求以及痛点,在此谢谢各位同学.
「另外羽毛也提供付费技术咨询的服务,有需求的同学可以公众号后台私信添加微信。」
今日技能你学废了吗?
本文由 mdnice 多平台发布