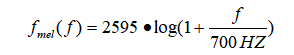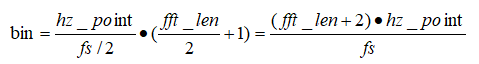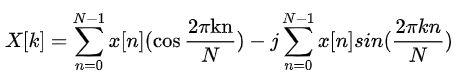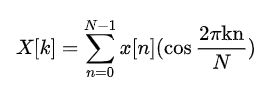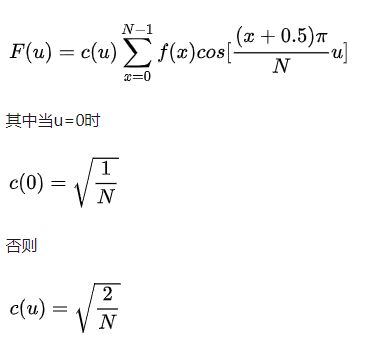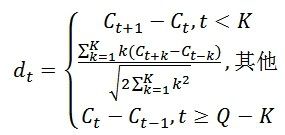AI大语音(四)——MFCC特征提取(深度解析)
本文来自公众号“AI大道理”。
这里既有AI,又有生活大道理,无数渺小的思考填满了一生。
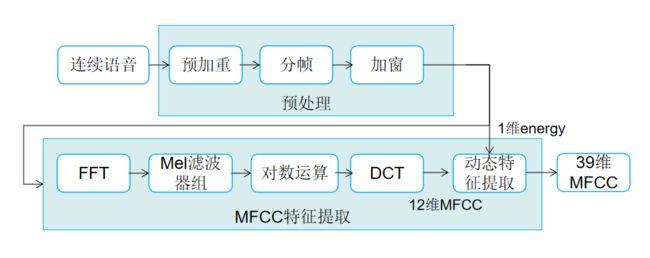
1 特征提取流程
在语音识别和话者识别方面,最常用到的语音特征就是梅尔倒谱系数(Mel-scaleFrequency Cepstral Coefficients,简称MFCC)。
MFCC提取过程包括预处理、快速傅里叶变换、Mei滤波器组、对数运算、离散余弦变换、动态特征提取等步骤。
2 快速傅里叶变换
快速傅里叶变换即利用计算机计算离散傅里叶变换(DFT)的高效、快速计算方法的统称,简称FFT。
FFT不是Fast FT,而是Fast DFT
FT的种类很多,以最简单的基于2的FFT为例。
FFT实际上一种分治算法。FFT将长度为N 的信号分解成两个长度为\frac{N}{2}信号进行处理,这样分解一直到最后,每一次的分解都会减少计算的次数。理解FFT分以下三个步骤进行:
步骤1:将信号x\left[n\right]分解成两个子信号 偶数样本点信号:x\left[2n\right]; 奇数样本点信号:x\left[2n+1\right];N=0,1,\cdots,\frac{N}{2}-1
步骤2:将两个求和项理解成两个长度为\frac{N}{2}的DFT
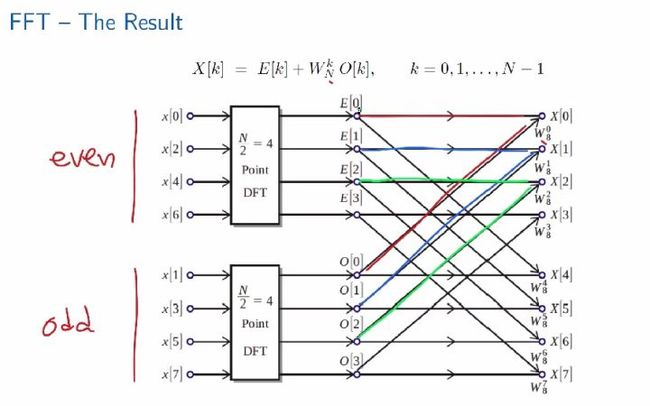
步骤3:FFT的具体计算过程
对于任意k都要进行N次加法操作,所以DFT共有N^2次乘法操作。 对于任意k都要进行N-1次加法操作,DFT共有N\left(N-1\right)次加法操作。 FFT共有N\left(\log_2N-1\right)次乘法操作和Nlog_2N次加法操作。
语音信号是有限长的离散信号。
预处理后的语音信号:
FFT后效果:
3 Mel滤波器组
将能量谱通过一组Mel尺度的三角形滤波器组,定义一个有M个滤波器的滤波器组(滤波器的个数和临界带的个数相近),采用的滤波器为三角滤波器,中心频率为 。M通常取22-26。各f(m)之间的间隔随着m值的减小而缩小,随着m值的增大而增宽,如图所示:
三角带通滤波器有两个主要目的:
(1)三角形是低频密、高频疏的,这可以模仿人耳在低频处分辨率高的特性;
(2)对频谱进行平滑化,并消除谐波的作用,突显原先语音的共振峰。频谱有包络和精细结构,分别对应音色与音高。对于语音识别来讲,音色是主要的有用信息,音高一般没有用。在每个三角形内积分,就可以消除精细结构,只保留音色的信息。
(3)傅里叶变换得到的序列很长(一般为几百到几千个点),把它变换成每个三角形下的能量,可以减少数据量
Mel频率和频率f的对应关系:
或者
Mel滤波器实现过程:
(1)确定最低频率(0HZ),最高频率(fs/2),Mel滤波器个数M(23);
(2)转换最低频率和最高频率的Mel(f);
(3)计算相连两个Mel滤波器中心Mel频率的距离,在Mel频率上,两两之间的中心频率是等间距的;
(4)将各种中心Mel频率转化为频率f(非等间距); (5)计算频率所对应的FFT中点的下标;
灵魂的拷问:为什么有些Mel滤波器组不等高,我设计的是等高的?这样有影响吗?有优势吗?
AI大语音:不等高的原因是乘了一个递减的系数,就是实现上一些细节的差别,保证了每个滤波器的能量和一样。横轴指的频率,低频的系数高,就是对低频更加的关注 。没有太大的影响,一般主要用等高的。
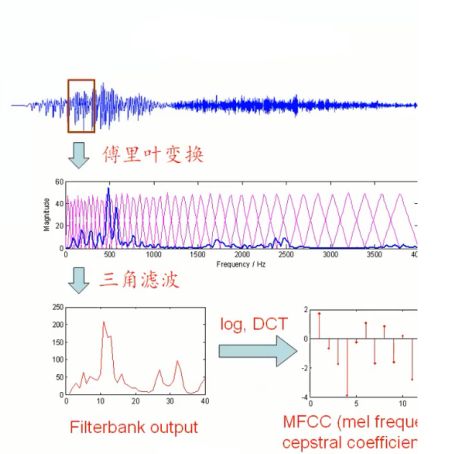
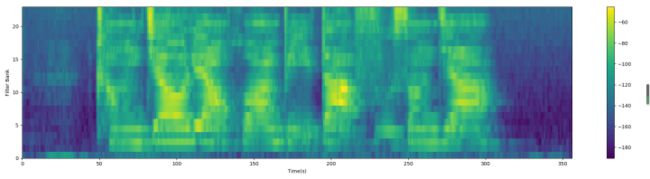
经过梅尔滤波器组后的Fbank特征:
4 对数运算
将原语音信号经过傅里叶变换得到频谱:
X[k]=H[k]E[k]
只考虑幅度就是:
|X[k] |=|H[k]||E[k] |
两边取对数:
log||X[k] ||= log ||H[k] ||+ log ||E[k] ||
再在两边取逆傅里叶变换得到:
x[k]=h[k]+e[k]
灵魂的拷问:为什么要进行对数运算?它在干嘛?
对数运算包括取绝对值和log运算。取绝对值是仅使用幅度值,忽略相位的影响,因为相位信息在语音识别中作用不大。
log运算是为了分别包络和细节,包络代表音色,细节带包音高,显然语音识别就是为了识别音色。另外,人的感知与频率的对数成正比,正好使用log模拟。
FFT变换后,卷积变成了乘法,取对数后,乘法变成了加法,把卷积信号转换成加性信号。
5 离散余弦变换(DCT)
再在两边取逆傅里叶变换得到:
x[k]=h[k]+e[k]
在上一步中,我们成功地把基音信息与声道信息变成了加性的。那么如何分离呢?它们有如下性质:
频谱图中(注意是一帧FFT变换内)
(1)基音信息在频域是快速变化的。
(2)声道信息在频域是缓慢变化的。
因此再做一次DCT可以将其分离。我们称之为"倒谱域"。因此倒谱域的低频部分刻画了声道信息,高频部分刻画了基音信息。
由此得到12维的MFCC特征:
由于许多要处理的信号都是实信号,在使用DFT时由于傅里叶变换时由于实信号傅立叶变换的共轭对称性导致DFT后在频域中有一半的数据冗余。 将DFT式子拆开,抽出实数部分:
则实数部分:
虚数部分:
又有:
而当x[n]是实偶信号时:
把DFT写成:
但是实际中并没有那么多实偶信号,我们就认为造出来。将信号长度扩大成原来的两倍,并变成2N,又为了让造出来的信号关于0对称,把整个延拓的信号向右平移 0.5 个单位,最终DCT变换公式:
6 动态特征提取
标准的倒谱参数MFCC只反映了语音参数的静态特性,语音的动态特性可以用这些静态特征的差分谱来描述。实验证明:把动、静态特征结合起来才能有效提高系统的识别性能。差分参数的计算可以采用下面的公式:
式中,dt表示第t个一阶差分,Ct表示第t个倒谱系数,Q表示倒谱系数的阶数,K表示一阶导数的时间差,可取1或2。将上式的结果再代入就可以得到二阶差分的参数。
因此,MFCC的全部组成其实是由: N维MFCC参数(N/3 MFCC系数+ N/3 一阶差分参数+ N/3 二阶差分参数)+帧能量(此项可根据需求替换)。
这里的帧能量是指一帧的音量(即能量),也是语音的重要特征。
d_mfcc_feat = delta(wav_feature, 1) d_mfcc_feat2 = delta(wav_feature, 2)
feature = np.hstack((wav_feature, d_mfcc_feat, d_mfcc_feat2))
最终39维MFCC图:
附录(魔鬼写手)
——————
浅谈则止,细致入微AI大道理
扫描下方“AI大道理”,选择“关注”公众号
—————————————————————
![]()
—————————————————————
投稿吧 | 留言吧
▼下期预告▼
AI大语音(五)——声学模型
▼往期精彩回顾▼
AI大语音(一)——语音识别基础
AI大语音(二)——语音预处理
AI大语音(三)——傅里叶变换家族
留你心,言你想