Pytorch学习笔记(一)——自动求导和叶子节点
一、什么是叶子节点
PyTorch中的张量tensor有一个属性是is_leaf,当is_leaf为True时,改tensor是叶子张量,也叫叶子节点。
二、叶子节点的作用
PyTorch有自动求导的功能,
当requires_grad=True时,PyTorch会自动记录运算过程,缓存运算中的中间参数,为自动求导做准备。
但是只有is_leaf=True和requires_grad=True同时满足时,才可以获得该节点的导数值。
三、什么样的节点为叶子节点
按照惯例:
1、所有requires_grad为False的张量(Tensor) 都为叶张量( leaf Tensor);
2、requires_grad为True的张量(Tensor),如果他们是由用户创建的,则它们是叶张量(leaf Tensor)。这意味着它们不是运算的结果,因此grad_fn为None。
>>> a = torch.rand(10, requires_grad=True)
>>> a.is_leaf
True
#a was created by user
>>> b = torch.rand(10, requires_grad=False)
>>> b.is_leaf
True
>>> c = torch.rand(10, requires_grad=True) + 2
>>> c.is_leaf
False
# c was created by the addition operation
四、自动求导的机理
每个方框代表一个tensor,其中列出一些属性(还有其他很多属性):
- .data: 存了tensor的data,即保存着张量的数值;
- .grad: 当计算梯度的时候,会在此保存该张量对应情况下的梯度值;
- .grad_fn:指向用于backward的函数的节点;
- .is_leaf 判断是否是叶节点;
- .requires_grad:如果是设为True,那么在做backward时候将作为反馈的一部分参与backwards运算,如果为False则不参加backwards运算。
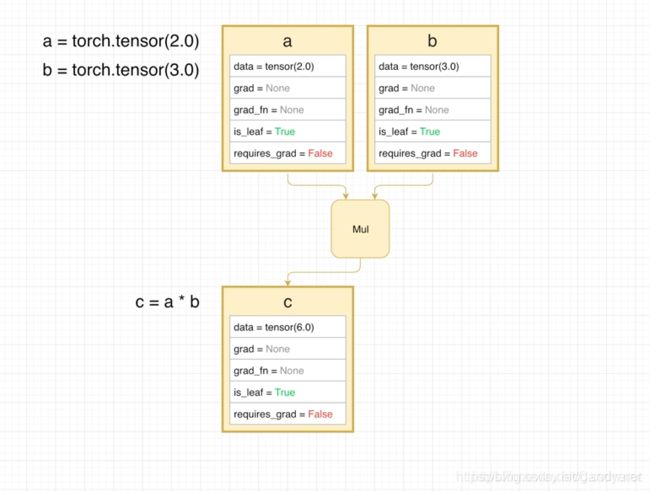
例一:
a = torch.tensor(2.0)
b = torch.tensor(3.0)
c = a*b
因为a,b的requires_grad都是False,所以没有记录其运算过程,也不需要求导数。
例二:
a = torch.tensor(2.0,requires_grad = True)
b = torch.tensor(3.0)
c = a*b
c.backward()
1、tensor a的 requires_grad 为True,因为输入自变量的属性为有一个为True,所以输出变量的属性自动改变成 requires_grad 为True。
这说明只要自变量中有一个requires_grad 为True, 进一步通过运算生成的变量也为True。因为 c 的 requires_grad 为True, c 又是运算产生的,所以其不是叶子节点。
2、当我们调用tensor的乘法函数时,同时调用了隐性变量 ctx (context)变量的save_for_backward(),此函数保存了forward运算时的一些参数,ctx起到了缓存相关参数的作用,在做 backfard 运算时, ctx中的值将会被对应的函数读取。
3、c的grad_fn中存了做backwards时候对应的函数— “MulBackward”,这个函数是PyTorch自动生成的。
4、当进行 c 的 backwards 的时候,其实也就相当于求解 c = a*b 这个函数分别对 a 与 b 做的偏导. 那么理应对应两组backwards的函数,这两组backwards的函数打包存在 MulBackward 的 next_functions 中. nex_function为一个 tuple list, AccumulateGrad 将会把相应得到的结果送到 a.grad中.
5、于是在进行 c.backward() 后, c进行关于a以及关于b的求导,由于b设requires_grad为False,因此b项不参与backwards运算(自然的,next_function中list的第二个tuple即为None),c关于a的梯度为3,因此3将传递给AccumulaGrad进一步传给a.grad 因此 a.grad 的结果为3。
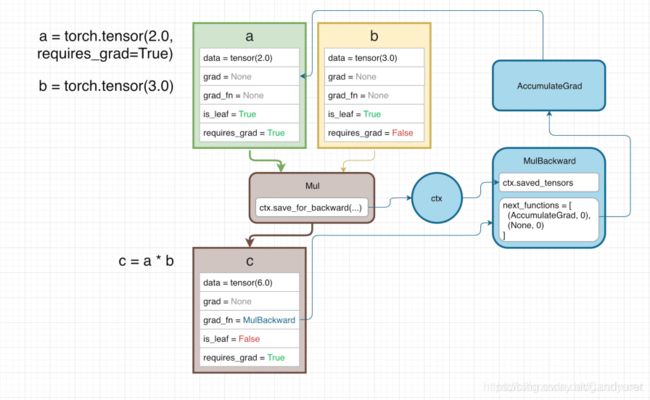
可以看出,其实pytorch在定义这些变量的运算函数时,其实也定义了函数对应的backwards的函数.如果想使用自定义的函数,那么自己也必须要定义backwards函数.
例三:
a = torch.tensor(2.0,requires_grad = True)
b = torch.tensor(3.0,requires_grad = True)
c = a*b
d = torch.tensor(4.0,requires_grad = True)
e = c*d
e.backward()
1、e的grad_fn 指向节点 MulBackward, c的grad_fn指向另一个节点 MulBackward
2、c 为中间值is_leaf 为False,因此并不包含 grad值,在backward计算中,并不需要再重新获取c.grad的值, backward的运算直接走相应的backward node 即可
3、MulBackward 从 ctx.saved_tensor中调用有用信息, e= c+d中 e关于c的梯度通过MulBackward 获取得4. 根据链式规则, 4再和上一阶段的 c关于 a和c关于b的两个梯度值3和2相乘,最终得到了相应的值12 和8
4、a.grad 中存入12, b.grad中存入 8

本文为学习PyTorch时的学习笔记,主要参考博文https://blog.csdn.net/wangweiwells/article/details/101174330和https://blog.csdn.net/wangweiwells/article/details/101223420