【论文学习】6、Wi-Fi中基于前导码的包检测：一种深度学习方法

摘要

基于ieee802.11标准系列的无线网络系统是最流行的使用先听后说（LBT）方法进行信道接入的无线接口，在非接触频段中工作。大多数基于LBT的系统的显著特征是，发射机使用数据之前的前导码来允许接收机获得初始信号检测和同步。在模拟到数字转换之后应用于传入的离散时间复基带样本的接收器处的第一数字处理步骤是分组检测步骤，即，检测到达传入流内的每个帧的初始样本。由于前导码通常包含具有良好相关特性的训练符号的重复，传统的数字接收机采用基于相关的方法来进行分组检测。基于数据的深度学习（DL）方法在物理层信号处理中的应用，本文提出了一种基于DL的Wi-Fi包检测方法。利用一维卷积神经网络（1D-CNN），我们对传统和基于DL的Wi-Fi包检测方法进行了详细的复杂度与性能分析和比较。
索引：深度学习，包检测，ieee802.11

介绍

为了保证公平性，在非许可频段工作的无线系统共享一种基于先听后讲（LBT）方法的公共信道接入方法。在这些系统中，到目前为止最普遍的是基于ieee802.11标准的Wi-Fi系统，这些标准应用了载波感知多址冲突避免（CSMA/CA）方法[1]。由于频谱稀缺，蜂窝系统还引入了在未经许可的频带中使用LBT方法，例如，在称为LTE-U的4G标准的未经许可版本中[2]。

在大多数LBT系统中，通常的方法是发射机向数据包发送前置码，以确保接收机检测到信号并获得初始同步。这种前导码通常被设计为具有良好相关特性的符号序列，允许接收端的信号处理算法识别分组起始样本[1]、[3]。具体地，在接收器侧，在信号被转换成离散时间复基带样本流之后，第一数字接收器块表示分组检测算法。传统的数字接收机采用基于相关的方法检测传入流[4]、[5]中到达的每个帧的初始样本。

近年来，基于数据的深度学习（DL）方法在无线接收端应用于信号处理任务时表现出优异的性能[6]，[7]。不同的研究集中在不同的物理层（PHY）信号处理任务上，包括信号检测[8]、信道估计[9]和纠错编码[10]。在一篇配套论文中，我们研究了IEEE 802.11系统中基于DL的信号检测和载波频偏（CFO）估计，并与传统算法对比评估了用于分组检测和CFO估计的各种DL架构[11]。在本文中，我们将重点放在数据包检测部分，并通过提供详细的复杂度与性能评估以及传统和基于DL的Wi-Fi数据包检测之间的比较来进一步分析。利用一维卷积神经网络（1D-CNN），我们对不同参数的1D-CNN结构与传统的基于相关的包检测器进行了细粒度的评估和比较，1D-CNN在序列检测方面的优异性能在[8]、[11]中得到了证明。我们的结果表明，一维CNN结构在性能和计算复杂度上都优于传统方法，同时在低信噪比（SNR）下保持鲁棒性。

论文的结构如下。以秒为单位。二、 我们提供了背景信息并给出了系统模型。以秒为单位。三、 我们回顾了传统的基于相关性的包检测，并给出了基于一维CNN的包检测的细节。详细分析了两种方法的复杂度与性能。四、 本文在第二节结束。五。

背景和系统模型

本文主要研究基于正交频分复用（OFDM）的ieee802.11技术。其中，基于具有良好相关特性的符号的重复模式的前导码被置于用于初始同步和/或信道估计的数据符号之前（图1）。初始同步过程包括：i）包检测，ii）采样时间偏移（TO）估计，以及iii）CFO估计[12]。

在不丧失通用性的前提下，为了实施和评估，我们重点关注用于Wi-Fi物联网（IoT）的IEEE 802.11ah（Wi-Fi HaLow）标准[13]。对于1mhz分组结构，802.11ah前导码包括14个OFDM符号，其中每个OFDM符号包含N＝32个子载波，子载波间隔为∆在频域中f=31.25 kHz。在时域中，每个OFDM符号由8的循环前缀扩展μs持续时间，导致40μs符号。序言分为三个领域：

短训练场（STF）：STF由4个OFDM符号组成，在IDFT之后，代表同一16个符号的10个重复μ时域中的s长-短训练符号（STS）。STS具有良好的相关性，适用于粗定时同步和粗CFO估计。
长训练场1（LTF1）：LTF1还包含4个160的OFDM符号μs持续时间。相同长训练符号（LTS）的两次重复可实现精细定时同步、CFO估计和信道估计。
信号场（SIG）：包含分组信息以配置接收器，而长训练场2（LTF2）用于MIMO信道估计，而在这里，我们关注单天线（SISO）传输。

图2示出总持续时间560的离散时间复基带802.11ah前导码的幅度μs。由于我们的重点是初始数据包样本的检测，为了减少模拟负载，我们使用802.11ah空数据包（NDP），它只包含前导码而不包含数据字段[12]。

在传输之前，对时域样本x进行过采样和滤波，得到过采样信号样本xos。针对离散时间复基带模型，通过等效离散时间冲激响应h来表示信道。添加复合加性高斯白噪声（AWGN）w样本，接收信号样本建模为：

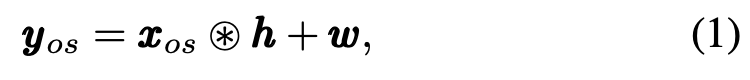
哪里 表示循环卷积。除了信道损伤和噪声外，接收信号还受到采样频率的影响ε 首席财务官呢∆ = fof/∆f需要估计和修正[4]。在接收端，信号经过反向脉冲形状滤波和下采样后，接收到的样本y被转发到分组检测，我们将在下一节中详细介绍。

基于前导码的包检测

A.传统的包检测方法

传统的包检测算法通过两个后续接收到的训练符号之间的复相关，采用重复的前导码结构。如果我们假设一个训练符号中的复样本数是L，那么这种复相关可以表示为：

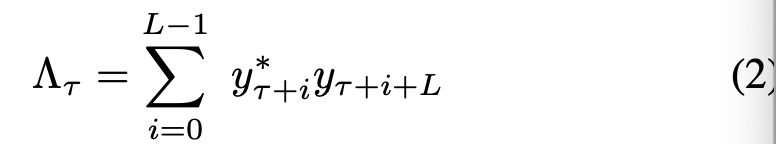
在文献[4]和[5]中，作者提出了一种分组检测算法，该算法基于这样一个假设：如果一个训练符号的共轭样本乘以相邻训练符号的对应样本，则信道效应将被消除。因此，这些样本对在帧开始处的乘积将具有大致相同的相位，因此它们的和的大小将是一个大值。为了降低算法的复杂度，他们引入了一个2L样本的窗口，该窗口沿时间滑动τ 当接收器搜索第一训练符号时，即，分组开始样本τS。用于包检测的时间度量是：

其中Pτ 是L个后续样本的幂之和：

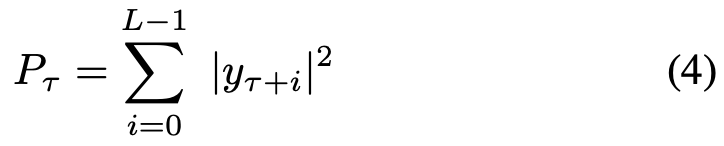
从时间度量M(τ), 可以通过找到使M最大化的样本来找到初始分组样本(τ). 另外，除了找到最大采样点外，在时域中观察位于最大值90%左右的点，并对这两个90%的时间样本进行平均，可以得到更准确的定时估计。触发上述算法的阈值的选择应使算法在控制虚警概率的同时最小化漏检概率。

ieee802.11中的包检测通常分为粗同步和精同步两个步骤，其中传统算法的主要原理被重用并适应特定的系统需求。粗包检测，表示为τˆS、 可遵循[4]（等式3），设置L=80个样本（STF持续时间的一半）：

其中lS是STS样本长度，lS表示STF字段的样本长度。之后τˆ因此，我们可以提取整个前导码，因为使用单个长训练符号和整个前导码之间的相关性的峰值来获得更精确的时间估计[1]。

B.基于深度学习的数据包检测

用于数据包检测的卷积神经网络：基于我们的配套论文[11]中的初步结果和[8]中的最新研究，我们考虑使用一维卷积神经网络（1D-CNN）进行Wi-Fi数据包检测，该网络在处理时间序列数据方面提供了出色的结果。

CNNs是一种在计算机视觉和图像分类问题上取得了突出成果的DL结构，因为它能够通过应用相关滤波器从局部输入中提取特征。CNN可以有效地学习层次特征，从而构建高级抽象的最终特征集，然后用于在更高层中形成更复杂的模式[14]。同样的想法也可以应用于一维数据序列，其中一维CNN被证明能有效地从固定长度的数据段中提取特征。1D-CNN的这一特性，加上1D卷积层是平移不变的（在信号中的某个位置学习的模式可以在另一个位置识别），使得这种结构适合于包检测任务。

在紧凑的一维CNN中应用了两种类型的层：i）发生一维卷积的一维CNN层和ii）完全连接（FC）层。每个隐藏层执行一个卷积序列，其总和通过激活函数传递[15]。1D-CNN代表的主要优点是将特征提取和分类操作融合到一个可以优化以最大化网络性能的过程中，因为CNN层处理原始1D数据并提取FC层用于预测任务的特征（图3）。因此，提供了较低的计算复杂度，并且如果与2D CNN相比，1D-CNN可以使用较大的滤波器和卷积窗口大小，因为唯一昂贵的操作是1D卷积序列。

数据集和训练过程：包检测问题可以描述为一个回归问题，其中CNN需要学习一个在输入信号和输出值之间的映射，表示包开始时刻，同时区别于噪声。我们假设基于CNN的包检测在接收信号幅度样本的连续固定长度块| y |上操作：

对接收到的信号进行下采样和滤波后。数据集由（| y |）组成，τS）成对，其中τS表示块内的数据包开始样本。在数据集中，我们包含了大约50%的块，这些块不包含packet start实例，并用τS=−1.在这些块中，大约一半只包含噪声样本，而另一半包含NDP包的中间部分或尾部。对于包含数据包开始时刻的数据集块τS、 其值在输入块样本中随机统一设置。为长度为40、80、160、320、800、1600个样本的输入块| y |创建数据集，其中每个数据集中接收的块数为50000。从数据集中，70%的记录用于训练，15%用于验证，15%用于测试。

不管输入块大小如何，所有数据包都使用符合标准的ieee802.11ah物理层模拟器在相同条件下进行模拟。为了检验估计对变化的信噪比（SNR）的鲁棒性，SNR值从[0 dB，25 dB]范围内均匀随机选取。在仿真过程中，采用了室内多径衰落信道模型B[16]。

为了训练DNN模型，均方误差（MSE）损失：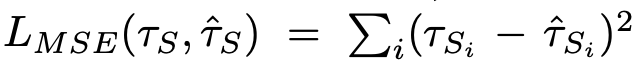
最小，因为我们观察到，与平均绝对误差（MAE）和Huber损失函数相比，该算法获得了更好的性能。训练集被分成大小为80的小批量，400个时间段就足以实现损失函数的收敛。为了优化网络参数，在学习速率下采用ADAM优化器的随机梯度下降（SGD）算法α = 0.001, β1=0.9和β2=0.999（详见[17]）。

所有实验都使用相同的1D-CNN结构，其参数设置如表I所示。选择第一卷积层的滤波器大小作为STS样本长度的一半（8个样本），并应用1个样本的步长（图3）。请注意，我们没有充分利用1D-CNN架构的灵活性，因为我们应用了固定数量的输入通道以及固定长度过滤器。我们采用这种固定的结构，使得算法的性能和复杂度分析变得更加容易。我们注意到，进一步优化输入通道的数量和输入滤波器的长度可以进一步改善性能与复杂性的权衡。最后，注意，输入块的长度越大，第一层的复杂度增加，然而，每单位时间要处理的块的数目减少。第二节对不同的网络进行了详细的研究。四、 B。

四、 数值结果

在本节中，我们讨论了基于CNN和传统方法在不同snr下的包检测性能，同时考虑了漏检率和虚警率。此外，我们还研究了所提出的基于CNN的分组检测算法在不同输入块长度下的计算复杂度，并以每秒浮点运算的近似次数（FLOPS）与传统方法进行了比较。

数据包检测性能：在以下实验中，为所有输入块长度的输入通道数选择的值设置为4。我们考虑了MAE性能，同时也考虑了漏检概率和虚警概率。图4显示了1D-CNN结构的MAE包检测性能，作为测试集上评估的接收SNR的函数。该图还包括获得的结果在粗、精包开始样本估计的基础上，采用常规方法。我们注意到，与传统方法相比，一维CNN方法对信噪比的变化表现出良好的鲁棒性，而传统方法的性能在信噪比较低时会恶化。此外，随着输入块长度的减小，一维CNN包检测器的性能优于传统方法。尽管这在很大程度上可归因于估计的分组开始样本值这一事实τS受输入块大小的限制（因此，通过减小输入块长度，估计误差自然减小），我们仍然注意到，对于输入块，1D CNN取320个样本，其性能与在80个样本的输入块上滑动的传统检测器相当（秒）。三、 对于低于7db的信噪比，其性能甚至优于传统检测器。

对于相同的设置，图5显示了不同输入块大小的漏检率和虚警率。结果表示为整个测试集（即，所有snr）上平均的未命中或错误检测包的百分比。比较而言，在相同的测试条件下，传统方法的漏检率为0.007%，虚警率为0.009%。对于基于1D-CNN的包检测器，尽管结果在输入块长度范围内变化，对于较小的输入块大小显示出特别高的误报率，但是对于较大的输入块长度，性能逐渐提高，实现低于0.1%的漏检率和误报率。

计算复杂性分析：图6给出了1D-CNN结构的触发器的近似数目与输入块长度的函数关系，其中包括常规方法以供参考。假设在我们的实验中使用的ieee802.11ah场景的采样率为1mhz，我们在图6中给出了具有相同输入信道数的1dcnns的触发器数。1D-CNN的每一层的复杂度可以通过计算每一层中的加法和乘法的数目来计算。一个CNN的触发器总数取决于输入块的大小，然而，请注意，虽然较大的输入块会导致更复杂的网络，但它们也会减少每秒处理的块数。根据文献[8]，单个卷积层的复杂度取决于滤波器长度F、输入（chi）和输出（cho）通道数以及输出宽度K，而FC层的复杂度取决于输入（Ni）和输出（No）大小。表II[8]给出了用于计算单层中的近似触发器数（乘法和加法）的数学表达式。

对于传统的包检测算法，重新调用它包括两部分：粗估计和精估计。在粗估计过程中，对长度为80个样本的输入块进行逐样本处理。通过计算长度为80个样本的单个输入块的乘法和加法的数目，乘以每秒处理的块的数目，导出用于粗包检测的FLOPS计数。精细估计的复杂度被忽略，而精细估计仅在粗略估计检测到包的开始时运行。

从图6可以看出，对于相同数量的输入信道，1D cnn的复杂度与传统算法相当，特别是对于较小的输入块长度。比较这些结果与图。4和5，我们注意到一维CNNs在降低接收端计算负担的情况下能够优于传统方法，同时在漏检率和虚警率方面仍然较低，这需要在搜索期望性能时进行适当的折衷。例如，我们注意到1D-CNN参数的值（输入通道数和滤波器输入长度），可以设法将1D-CNN的复杂度保持在长度为800个样本的输入块的传统算法的复杂度以下。因此，1D-CNN为平衡MAE性能、MFLOPs计算量、漏检率和虚警率提供了广泛的操作范围。

五、结论

在本文中，我们深入研究了用于Wi-Fi中基于前导码的数据包检测的一维CNN结构。结果表明，与传统方法相比，一维CNNs具有良好的性能和复杂度。我们正在进行的工作是在真实的室内环境中使用软件定义的无线电演示这些结果。

六、 致谢

这项工作得到了欧盟地平线2020研究与创新计划（Horizon 2020 research and innovation programme）的资助，资助协议编号为856967。

引用

REFERENCES
[1] E. Perahia and R. Stacey, Next Generation Wireless LANs: Throughput, Robustness, and Reliability in 802.11n, Cambridge Univ. Press, 2008.
[2] A. Mukherjee, J.F. Cheng, S. Falahati, H. Koorapaty, R. Karaki, L. Falconetti, D. Larsson, “Licensed-assisted access LTE: coexistence with IEEE 802.11 and the evolution toward 5G,” IEEE Communications Magazine, 54(6), pp. 50-57, 2015.
[3] S. Nagaraj, S. Khan, C. Schlegel, M. Burnashev, “On preamble detec- tion in packet-based wireless networks,” IEEE Int’l Symp. on Spread Spectrum Techniques and Applications, pp. 476–480), 2006.
[4] T. M. Schmidl and D. C. Cox, “Robust frequency and timing synchro- nization for OFDM,” IEEE Trans. on Commun., pp. 1613–1621, 1997. [5] A.vanZelst,andT.C.W.Schenk,“ImplementationofaMIMOOFDM- based wireless LAN system,” IEEE Trans. on Signal Processing, vol. 52,
pp. 483-494, 2004.
[6] T. OShea, J. Hoydis, “An introduction to deep learning for the physical
layer,” IEEE Trans. Cogn. Comm. and Netw., 3(4), pp.563-575, 2017. [7] Z. Qin, H. Ye, G.Y. Li, B.H.F. Juang, “Deep learning in physical layer
communications,” IEEE Wireless Comm., 26(2), pp.93-99, 2019.
[8] T.O’Shea,K.Karra,T.C.Clancy,“Learningapproximateneuralestima-
tors for wireless channel state information,” IEEE MLSP 2017, Japan. [9] H. Ye, G.Y. Li, B.H. Juang, “Power of deep learning for channel estimation and signal detection in OFDM systems,” IEEE Wireless
Communications Letters, 7(1), pp.114-117, 2017.
[10] E. Nachmani, E. Marciano, L. Lugosch, W.J. Gross, D. Burshtein, Y.
Beery, “Deep learning methods for improved decoding of linear codes,”
IEEE Journ. Sel. Topics Sign. Proc., 12(1), pp.119-131, 2018.
[11] V. Ninkovic, D. Vukobratovic, A. Valka, D. Dumic, “Deep Learning Based Packet Detection and Carrier Frequency Offset Estimation in IEEE 802.11ah.” preprint, available at: https://arxiv.org/abs/2004.11716. [12] K. S. Kim, S. W. Kim, Y. S. Cho, and J. Y. Ahn, “Synchronization and cell-search technique using preamble for OFDM cellular systems,” IEEE
Trans. Veh. Teh. Technol., vol. 56, pp. 34693485, 2007.
[13] IEEE 802.11 ah-2016 Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications - Amendment 2: Sub
1 GHz License Exempt Operation, Dec. 2016.
[14] Y. LeCun, L. Bottou, Y. Bengio and P. Haffner, “Gradient-based learning
applied to document recognition,” in Proc. of the IEEE, vol. 86, pp.
2278-2324, 1998.
[15] S. Kiranyaz, T. Ince, O. Abdeljaber, O. Avci and M. Gabbouj, “1-D
Convolutional Neural Networks for Signal Processing Applications,”
ICASSP 2019, Brighton, UK, pp. 8360-8364., 2019.
[16] R.Porat,S.K.Yong,K.Doppler.“IEEEP802.11WirelessLANsTGah-
Channel Model ”, Proposed Text doc.: IEEE 802.1111/0968r4. 2015. [17] D. P. Kingma, J. L. Ba, “Adam: A method for stochastic optimization”,
Proc. Int. Conference on Learning Representation, pp. 1-41, 2015.