Joint Transceiver Optimization for Wireless Communication PHY Using Neural Network

Abstract

Deep learning has a wide application in the area of natural language processing and image processing due to its strong ability of generalization. In this paper, we propose a novel neural network structure for jointly optimizing the transmitter and receiver in communication physical layer under fading channels. We build up a convolutional autoencoder to simultaneously conduct the role of modulation, equalization, and demodulation. The proposed system is able to design different mapping scheme from input bit sequences of arbitrary length to constellation symbols according to different channel environments. The simulation results show that the performance of neural network-based system is superior to traditional modulation and equalization methods in terms of time complexity and bit error rate under fading channels. The proposed system can also be combined with other coding techniques to further improve the performance. Furthermore, the proposed system network is more robust to channel variation than traditional communication methods.

深度学习由于其较强的泛化能力，在自然语言处理和图像处理领域有着广泛的应用。本文提出了一种新型的神经网络结构，用于在衰减信道下联合优化通信物理层中的发射机和接收机。我们建立了一个卷积自动编码器，同时进行调制、均衡和解调的作用。所提出的系统能够根据不同的信道环境，从输入任意长度的比特序列到星座符号设计不同的映射方案。仿真结果表明，在衰落信道下，基于神经网络的系统在时间复杂度和误码率方面的性能优于传统的调制和均衡方法。所提出的系统还可以与其他编码技术相结合，进一步提高性能。此外，与传统通信方法相比，所提出的系统网络对信道变化的适应性更强。

II. DEEP LEARNING BASICS

The structure of layers we are going to use are plotted in Fig. 1. Dense layer is the layer that has each neuron connected with every neuron in the previous layer. In convolutional layer, each neuron is only connected to several nearby neurons in the previous layer (no more than 3 neurons in Fig. 1), and the parameters for each neuron are shared. The locally-connected layer works similarly to the convolutional layer, except that weights are unshared, that is, a different set of filters is applied at each different patch of the input. And the time-distributed dense layer is a layer that only processes every temporal slice of its input instead of all the elements of the input. Under our case, it is essentially a convolutional layer with kernel size = 1. Taking the application in communication PHY into consideration, we will provide further comparison between dense layer and convolutional layer in Section III.

我们要使用的层的结构如图1所示。稠密层是指每个神经元都与上一层的每个神经元相连的层。在卷积层中，每个神经元只与上一层中几个附近的神经元相连（图1中神经元不超过3个），每个神经元的参数是共享的。局部连接层的工作原理与卷积层类似，只是权重是不共享的，即在输入的每个不同的补丁处应用不同的滤波器组。而时间分布稠密层是一个只处理输入的每个时间片而不是输入的所有元素的层。在我们的情况下，它本质上是一个卷积层，内核大小=1。考虑到在通信PHY中的应用，我们将在第三节对稠密层和卷积层进行进一步的比较。

III. SYSTEM MODEL

A. Traditional Communication PHY Structure

B. Comparison Between Machine Learning Techniques

Inspired by recent progress in machine learning, we may view the traditional communication system as a general optimization problem provided parameterized representation of g1 and g3. Since it remains unclear how to do parametrization and optimization, we briefly compare existing representative machine learning techniques, including boosted tree,dense neural network autoencoder (DNN-AE) and convolutional neural network autoencoder (CNN-AE). In most of previous literatures [20]–[23], DNN-AE is adopted as the basic structure of design.

受机器学习最新进展的启发，我们可以将传统的通信系统看作是一个一般的优化问题，提供参数化表示的g1和g3。由于目前仍不清楚如何进行参数化和优化，我们简单比较一下现有的代表性机器学习技术，包括boosted tree、稠密神经网络自动编码器（DNN-AE）和卷积神经网络自动编码器（CNN-AE）。在以往的文献[20]-[23]中，大多采用DNN-AE作为设计的基本结构。

Although DNN-AE may have a similar error rate as CNN-AE, we would like to point out that there is a huge computation complexity gap between these two network structures. Consider a simple case when a k-bit input sequence is processed by a one-layer CNN or DNN with 1 dimension. Assume the window size of CNN is c1 and the number of neurons for DNN is c2. Then the number of parameters in CNN is approximately c1 + 1, which does not scale with k, while the number of parameters in DNN is c2(k + 1). In practice, we tend to deal with input bits that are quite long even under block code setting. Thus it is more computationally efficient to train a CNN based autoencoder. As a concrete example, assuming that we are processing 12000 bits as input, if we assume the overall rate is 1/4, then the middle layers must have at least 6000 neurons, which could result in a huge number of parameters (at least 12000*6000) that makes the neural network hard to train.

虽然DNN-AE可能具有与CNN-AE相似的错误率，但我们要指出的是，这两种网络结构之间存在着巨大的计算复杂性差距。考虑一个简单的案例，当一个k位的输入序列被一个1维的单层CNN或DNN处理。假设CNN的窗口大小为c1，DNN的神经元数量为c2。那么CNN的参数数大约为c1+1，不随k的增加而增加，而DNN的参数数为c2(k+1)。在实际工作中，我们往往会处理相当长的输入位，即使在块码设置下也是如此。因此，训练一个基于CNN的自动编码器在计算上更有效率。举个具体的例子，假设我们要处理12000位的输入，如果我们假设总码率为1/4，那么中间层至少要有6000个神经元，这可能会导致大量的参数（至少12000*6000），导致神经网络难以训练。

Furthermore, it is also important that the proposed structure is able to be adapted to input with different lengths after training. However, for DNN-AE and boosted tree, one needs to retrain the whole model for input of different lengths. It is natural to adopt a CNN based structure since traditional communication system is mostly on a convolutional or similar scheme (e.g. convolution code, QAM and PSK modulation etc.). We summarized our discussion on different machine learning methods in Table I. Based on the properties of different machine learning methods, we propose to use a CNN autoencoder for joint transceiver optimization for the complexity consideration.

此外，同样重要的是，所提出的结构能够在训练后适应不同长度的输入。然而，对于DNN-AE和boosted tree来说，人们需要对整个模型进行再训练，以适应不同长度的输入。由于传统的通信系统多采用卷积或类似的方案(如卷积码、QAM和PSK调制等)，因此采用基于CNN的结构是很自然的。我们在表一中总结了对不同机器学习方法的讨论。根据不同机器学习方法的特性，出于复杂度的考虑，我们提出采用CNN自动编码器进行联合收发优化。

IV. AUTOENCODER FOR TIME DOMAIN TRANSMISSION

A. Network Structure

The property of neural network enables us to train the model using only input bit sequences under different channel states. We jointly optimize the transmitter and receiver with an autoencoder structure. Convolutional neural network is used considering the sequential property of the input sequence. The network structure is shown in Fig. 3.

神经网络的特性使我们能够在不同的信道状态下，只使用输入位序列来训练模型。我们用自动编码器结构联合优化发射机和接收机。考虑到输入序列的顺序性，采用卷积神经网络。网络结构如图3所示。

We compress the length of the input from k×M to M in the first convolutional layer with stride size = k. And we combine the usage of time-distributed dense layer with convolutional layer to introduce further correlation and nonlinearity in the transmitter. We increase the number of parameters in the second convolutional layer to further improve the representability of the network. This is inspired by the traditional practice in communication of first doing coding to introduce redundancy and then conducting modulation to compress the data. The transmitted symbol X = [real(x);imag(x)] is of size M × 2 as a complex vector. In the channel layer, the input symbols are first normalized to satisfy the power constraint. For AWGN channel, only additive white gaussian noise is added to the normalized symbols. For fading channels, the normalized symbols first convolve with the impulse response in the time domain. The convolution in complex number is implemented as in equation (4). In neural networks, it can be represented by a 1D convolutional layer that convolves X with a 3D tensor.

在第一卷积层中，我们将输入的长度从k×M压缩到M，步幅大小=k，并结合时间分布密集层和卷积层的使用，在发射机中进一步引入相关性和非线性。我们增加了第二卷积层的参数数量，以进一步提高网络的可表示性。这是受传统通信中先做编码引入冗余，再进行调制压缩数据的做法的启发。传输的符号X=[real(x);imag(x)]是大小为M×2的复数向量。在信道层，首先对输入符号进行归一化处理，以满足功率约束。对于AWGN信道，只在归一化符号中加入加性白高斯噪声。对于衰落信道，归一化后的符号首先与时域的脉冲响应进行卷积。复数卷积的实现方式如式(4)。在神经网络中，可以用一个1D卷积层来表示，用3D张量来卷积X。

Generally a neural network suffers from the restriction of input shape, i.e. the length of input for testing shall be the same as that in training procedure. However, due to the locallyconnected property of convolutional layer and time-distributed layer, the proposed network structure is able to accept input sequences of any length without the need of retraining the whole model. Thus the system can process long sequences while trained on short ones.

一般来说，神经网络受到输入形状的限制，即用于测试的输入长度应与训练过程中的输入长度相同。然而，由于卷积层和时间分布层的局部连接特性，所提出的网络结构能够接受任何长度的输入序列，而不需要重新训练整个模型。因此该系统可以在对短序列进行训练的同时处理长序列。
We conduct massive experiments to analyze the performance of our model. We train our model separately on AWGN channel and fading channel. In the rest part of this chapter, we give a thorough analysis on the result of the learned system.

我们进行了大量的实验来分析我们模型的性能。我们分别在AWGN信道和衰落信道上训练我们的模型。在本章的其余部分，我们对学习系统的结果进行了全面的分析。
B. Setting

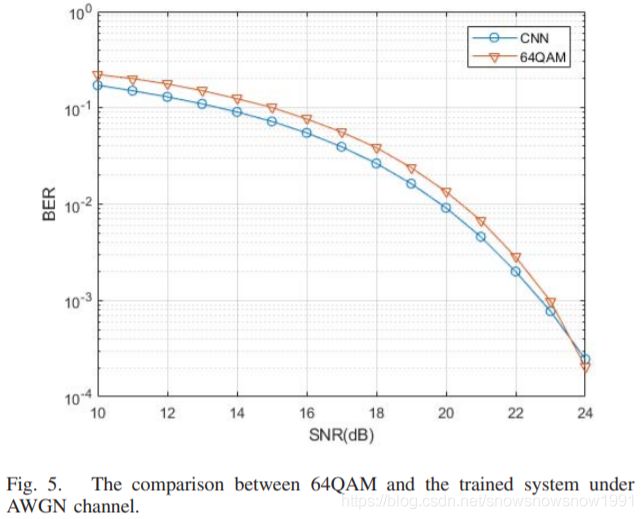
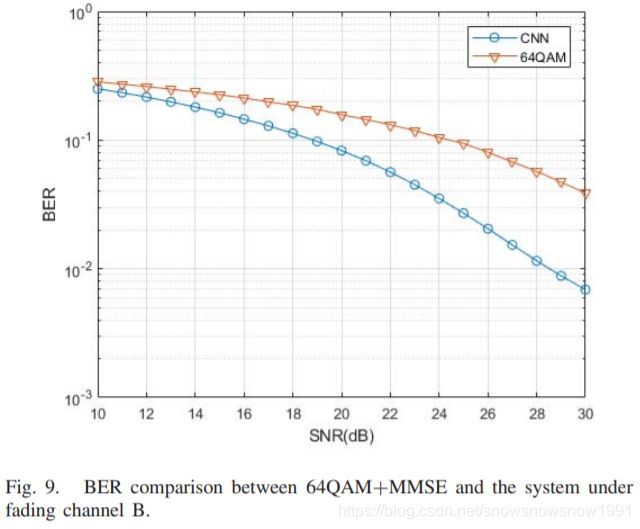
In our experiment, we set k = 6 and compare the learned system with 64QAM for AWGN channel, and 64QAM plus minimum mean square error (MMSE) estimation [28] for fading channel. We also test the proposed model on k = 8 case with 256QAM+MMSE in fading channel to prove the extensibility of our model. The modulation scheme is selected considering the throughput fairness. For the training and testing our model, we randomly generate i.i.d. bit sequences. The generated dataset is separated arbitrarily into training set, validation set and test set. The property of convolutional neural network enables the network to process input sequence of any length without changing network parameters. The change in the length of the input sequence would not affect the performance of our system. Thus we fix M to be 400.

在实验中，我们设置k=6，并将学习到的系统与AWGN信道的64QAM和衰落信道的64QAM加最小均方误差(MMSE)估计[28]进行比较。我们还在k=8的情况下用256QAM+MMSE在衰落信道中测试所提出的模型，以证明我们模型的可扩展性。调制方案的选择考虑了吞吐量的公平性。对于训练和测试我们的模型，我们随机生成i.i.d.比特序列。生成的数据集被任意分离为训练集、验证集和测试集。卷积神经网络的特性使得网络可以在不改变网络参数的情况下处理任意长度的输入序列。输入序列长度的改变不会影响我们系统的性能。因此我们将M固定为400。
We train the autoencoder with 30,000 training samples and test that with 10,000 test data. The learning rate is set to be 0.001 and the batch size is 32. We use mean squared error as the loss function. We run for 300 epochs. The kernel size of each convolutional layer is set to be 12 and we use tanh as activation function. We train the system at a specific signal to noise ratio (SNR) but test at a wide range of SNR, as well as robustness and adaptivity to deviations from the AWGN and fading setting. We would like to show that although the state space of input bit sequence is as large as , the model can generalize well with mere 30,000 training samples.

In the time domain transmission system, we test three different channels, one AWGN channel and two fading channels. The amplitude and delay for two fading channels are plotted in Fig. 4. The integer in x-axis is the delay of each path in the unit of symbols. Note that the phase information is omitted in the figure.

我们用30000个训练样本训练自动编码器，用10000个测试数据进行测试。学习率设置为0.001，批次大小为32。我们使用均方误差作为损失函数。我们运行了300个epochs。每个卷积层的内核大小设置为12，我们使用tanh作为激活函数。我们在特定的信噪比（SNR）下对系统进行训练，但在很宽的SNR范围内进行测试，以及对AWGN和衰减设置的偏差进行鲁棒性和适应性测试。我们想证明，虽然输入比特序列的状态空间大到，但仅用3万个训练样本，模型就能很好地泛化。

在时域传输系统中，我们测试了三个不同的信道，一个AWGN信道和两个衰落信道。图4中绘制了两个衰落信道的振幅和延迟。x轴中的整数是以符号为单位的每条路径的延迟。注意图中省略了相位信息。

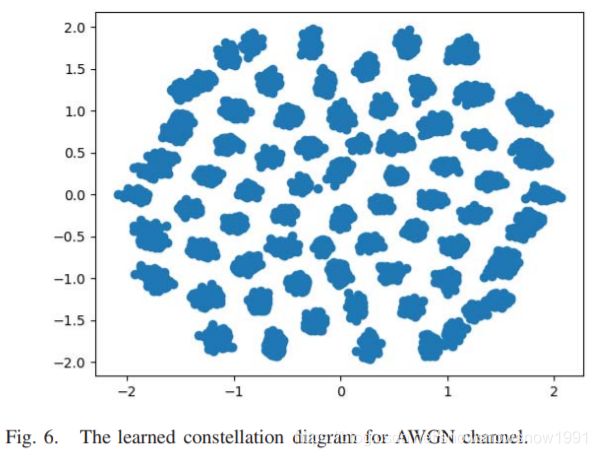
C. AWGN Channel

D. Fading Channel

low-density parity-check（LDPC）

E. Robustness

F. Time Complexity Comparison

We provide both simulation and numerical analysis for analyzing time complexity. We first test the time complexity by running demodulation plus detection algorithms and the receiver part in neural network on a Intel (R) Corel (TM) i7-7700HQ CPU @ 2.80GHz CPU and an NVIDIA GeForce GTX 1060 GPU. The platform in this experiment is python+keras [31]. For AWGN channel, only demodulation is needed to recover the bit sequence. For fading channel, MMSE is also included in the receiver, which takes long for the FFT step. We test both methods for 100 sets of data and take the average. The comparison is shown in Table.II. 

我们提供仿真和数值分析来分析时间复杂度。我们首先在英特尔(R)Corel(TM)i7-7700HQ @ 2.80GHz CPU和NVIDIA GeForce GTX 1060 GPU上运行解调加检测算法和神经网络中的接收器部分，测试时间复杂度。本实验中的平台是python+keras[31]。对于AWGN信道，只需要解调恢复比特序列。对于衰落信道，接收机中还包含MMSE，这需要很长的FFT步骤。我们对两种方法进行100组数据测试，取平均值。比较结果如表.II所示。

For transmitted bit sequence with length n, the time complexity for both CNN and QAM demodulation is O(n). However, for MMSE detection, FFT requires a O(nlogn). CNN is able to substitute the demodulation plus detection algorithm with a lower time complexity in theory and higher accuracy. Thus CNN based framework is quite suitable for designing communication system in fading channels.

对于长度为n的传输位序列，CNN和QAM解调的时间复杂度均为O(n)。但对于MMSE检测，FFT需要O(nlogn)。CNN能够替代解调加检测算法，理论上时间复杂度更低，精度更高。因此基于CNN的框架相当适用于设计衰落信道中的通信系统。

With the development of neural network, the dimension of the CNN can be potentially reduced with techniques such as network pruning and distillation. Parallelization is also possible in the multiplicative units in the neural network, as well as pipelining. Neural network can be further accelerated by specially designed hardware framework like GPU, FPGA and TPU etc. These designs along with a careful analysis of the fixed point arithmetic requirements of the different weights are under active research. The efficiency of neural network can be further improved in the future.

随着神经网络的发展，CNN的维度可以通过网络修剪和提炼等技术进行潜在的降低。神经网络中的乘法单元也可以实现并行化，以及管道化。神经网络可以通过专门设计的硬件框架，如GPU、FPGA和TPU等进一步加速。这些设计以及对不同权重的定点运算要求的仔细分析正在积极研究中。未来可以进一步提高神经网络的效率。

V. AUTOENCODER FOR FREQUENCY DOMAIN TRANSMISSION

A. Network Structure

In the previous chapter, we studied the effect of the multipath fading channel. In Orthogonal Frequency Division Multiplexing (OFDM) [32] system, the inter-symbol interference can be eliminated by introducing guard interval between each subcarrier. Cyclic prefix is a typical guard interval, which makes each subcarrier orthogonal to each other. In the following part of this chapter, we assume perfect cyclic prefix as guard interval. Thus there is no inter-symbol inference and inter-channel inference. However, there is still fading on each subcarrier. One of the most common equalization methods for this issue is zero forcing (ZF) [33]. Since the fading on individual subcarrier might be quite significant, it is hard to recover the signal from those subcarriers due to poor SNR. The information carried by some subcarriers might experience deep fading and thus get lost during transmission. A zero order equalization system would cause inevitable loss of information [34]. By introducing correlation between subcarriers, the information can be carried by nearby subcarriers. Thus the burst error on subcarriers with deep fading can be decreased.

在上一章中，我们研究了多径衰落信道的影响。在正交频分复用(OFDM)[32]系统中，可以通过在每个子载波之间引入保护间隔来消除符号间的干扰。循环前缀是一个典型的保护间隔，它使每个子载波之间正交。在本章的下面部分，我们假设完美的循环前缀作为保护间隔。因此，不存在符号间推理和信道间推理。然而，在每个子载波上仍然存在衰减。对于这个问题，最常用的均衡方法之一是迫零均衡（ZF）[33]。由于单个子载波上的衰落可能相当大，由于SNR较差，很难从这些子载波上恢复信号。一些子载波所携带的信息可能会经历深度衰落，从而在传输过程中丢失。零阶均衡系统会造成不可避免的信息丢失[34]。通过引入子载波之间的相关性，信息可以由附近的子载波携带。因此可以降低具有深度衰落的子载波的突发误差。

Based on previous network structure, we design a frequency domain equalization system that is able to retrieve more information than ZF. Since the fading on each subcarrier is different, a convolutional layer that shares weight along the whole input sequence may not be suitable. Here locally connected layer is used to substitute some of the convolutional layers in previous structure. The locally connected layer works similarly as the convolutional layer, except that weights of kernels are unshared. That is, a different set of filters is applied at each different patch of the input. The whole network structure is shown in Fig. 13.

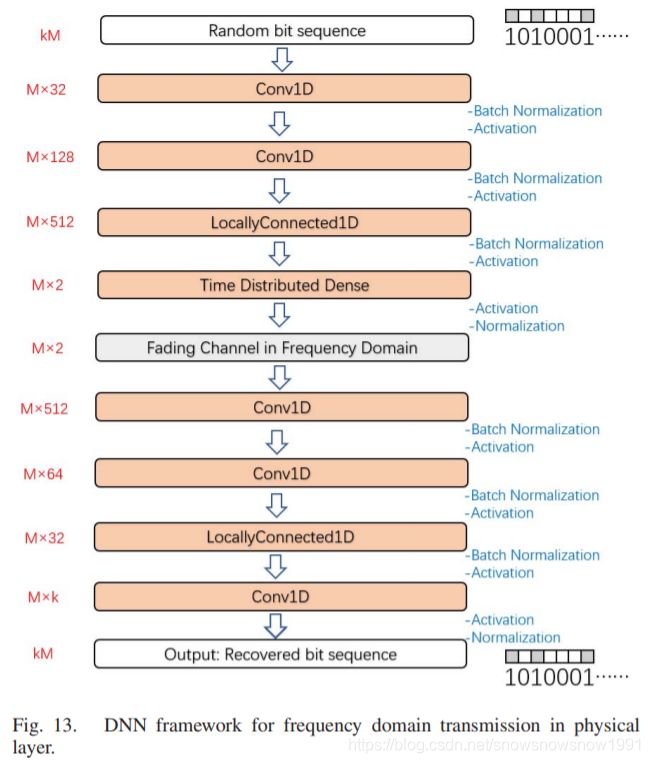
在以往网络结构的基础上，我们设计了一个频域均衡系统，它能够检索到比ZF更多的信息。由于每个子载波上的衰落是不同的，沿整个输入序列共享权重的卷积层可能并不合适。这里使用局部连接层来替代前面结构中的一些卷积层。局部连接层的工作原理与卷积层类似，只是核的权重是不共享的。也就是说，在输入的每一个不同的batch上都应用了一组不同的滤波器。整个网络结构如图13所示。

The only difference between time domain and frequency domain is the substitution of some convolutional layer. The reason to substitute convolutional layer with the more general locally connected layer lies in the fact that channel may bring different level of fading effects to different symbols on the coded sequence. Intuitively, the symbols that suffer from severe fading would need to spread its information to nearby symbols, while the symbols with strong energy also need to help carry more information. If we are merely using convolutional layer, then each symbol is treated equally, energy allocation is impossible to be done.

时域和频域之间唯一的区别就是替换了一些卷积层。用更一般的局部连接层代替卷积层的原因在于，信道可能会给编码序列上的不同符号带来不同程度的衰落影响。直观地讲，受到严重衰减影响的符号需要将其信息传播给附近的符号，而能量强的符号也需要帮助携带更多的信息。如果我们仅仅使用卷积层，那么每个符号都被平等对待，能量分配是不可能完成的。

B. Simulation

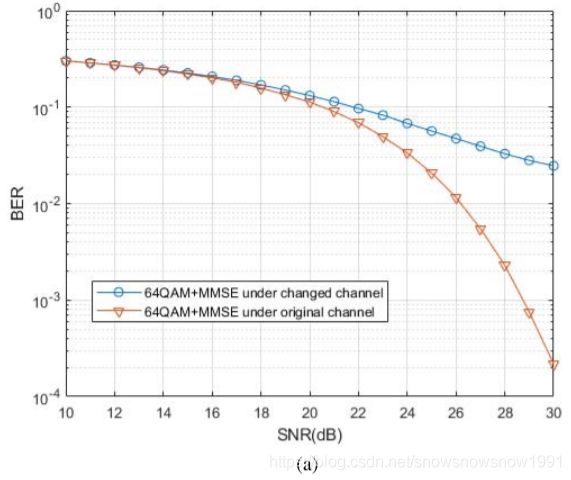
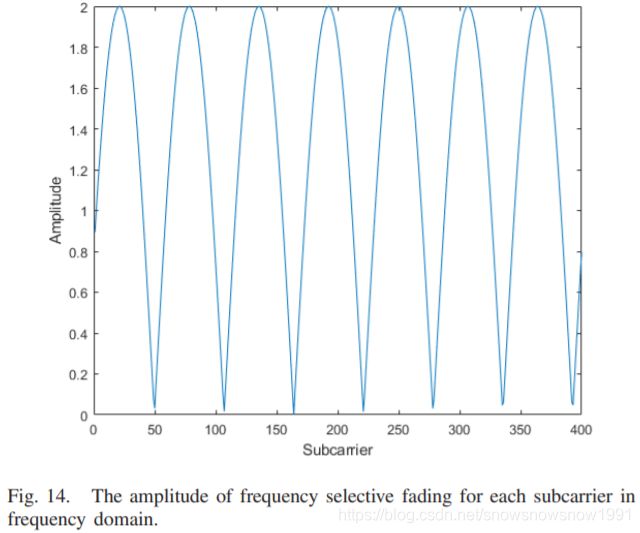
We test the new structure under the case of an OFDM system transmission. The bit sequence is modulated and transmitted in frequency domain. All other settings are the same as the previous example. We consider the frequency transformation of channel B in Fig. 4. The frequency selective fading channel in frequency domain is shown in Fig. 14. We train and test our model on the same channel. And compare that with 64QAM+ZF method. Here ZF is assumed to have accurate channel state information. But the zero points in the fading plot would prohibit a significant number of subcarriers from transmitting information to the receiver.

我们在OFDM系统传输的情况下测试了新的结构。比特序列在频域内被调制和传输。所有其他设置与前面的示例相同。我们在图4中考虑信道B的频率变换。频域中的频率选择性衰落信道如图14所示。我们在同一个频道上训练和测试我们的模型。并与64QAM+ZF法进行比较。这里假设ZF具有准确的信道状态信息。但是，衰落图中的零点将禁止大量的子载波向接收机发送信息。

VI. DISCUSSION

From previous two sections, we provide empirical justification on the superiority of our design. We are comparing the trained CNN-AE with mostly 64QAM+MMSE as a baseline. In communication area there are much more complex algorithms and techniques, e.g. iterative demodulation and decoding algorithm, that are able to achieve near-capacity performance in terms of BER. However, we justify the fairness of our comparison from the following three aspects.

在前两部分中，我们提供了我们的设计优越性的经验证明。我们正在比较训练的CNN-AE和大部分64QAM+MMSE作为基线。在通信领域，有很多复杂的算法和技术，例如迭代解调和解码算法，能够在误码率方面达到接近容量的性能。但是，我们从以下三个方面来证明我们的比较是公平的。

• The running time in Table II shows that our algorithm is comparable in efficiency to QAM+MMSE system. And there have been many mature ideas to make large neural networks practically implementable in small devices with due accuracy and faster speed [36]. For example, the idea of distilling the knowledge in a large network to a smaller network and the idea of binarization of weights and data in order to avoid complex multiplication operations could further speed up CNN-AE based communication system. 
• The designed CNN-AE does not include an iterative decoding structure. We believe that with appropriate iterative decoding design, the performance could be further improved and comparable with other coding and decoding methods using iterative schemes. For example, one may introduce another network as the second decoder and cascade that with the first decoder for the iterative decoding. Since the output of network can be viewed as the probability, it is naturally suitable for soft-decoding.
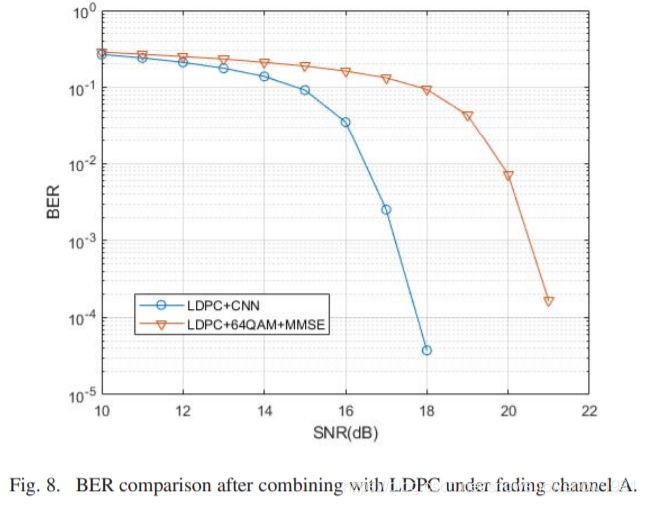
• With the help of interleaving, CNN-AE can also be combined with existing coding scheme to further improve its performance. We have shown previously that it can be combined with LDPC code in Fig. 8.
• 从表二的运行时间可以看出，我们的算法在效率上与QAM+MMSE系统相当。而为了使大型神经网络在小型设备中实际实现，并具有应有的精度和更快的速度，已经有很多成熟的想法[36]。例如，将大型网络中的知识提炼为一个较小的网络，以及将权值和数据二值化以避免复杂的乘法运算的思想，可以进一步加快基于CNN-AE的通信系统的速度。
• 所设计的CNN-AE不包括迭代解码结构。我们认为，如果采用适当的迭代解码设计，可以进一步提高性能，与其他采用迭代方案的编解码方法相媲美。例如，可以引入另一个网络作为第二解码器，与第一解码器级联，进行迭代解码。由于网络的输出可以看作是概率，所以自然适合软解码。
• 在交织的帮助下，CNN-AE还可以与现有的编码方案相结合，进一步提高其性能。前面我们已经展示了它可以与LDPC码结合，如图8。

Another issue with most of deep learning based communication system is that the BER stops decreasing after reaching some low BER level. This also shows up in our Figs. 11 and 15. However, for practice use, we propose to combine CNN-AE with some other coding scheme. When the coding is powerful enough, the system can reach much lower BER as long as the performance of CNN-AE is better within region.
Furthermore, we would like to point out that our goal is to show that CNN-AE is able to learn the way of mapping and demapping for any channel without prior mathematic model and analysis, thus being promising for communication system design without expertise. We also believe that some other autoencoder-based structures, e.g. combining resnet with autoencoder, may also lead to improvement on existing structures.

大多数基于深度学习的通信系统的另一个问题是，误码率在达到一些低误码率水平后就停止下降。这在我们的图11和图15中也有体现。但在实际使用中，我们建议将CNN-AE与其他编码方案相结合。当编码足够强大时，只要CNN-AE的性能在区域内更好，系统可以达到更低的误码率。
此外，我们想指出的是，我们的目标是证明CNN-AE能够在不需要事先建立数学模型和分析的情况下学习任何信道的映射和解映射方式，因此在没有专业知识的情况下，很有希望用于通信系统设计。我们也相信，其他一些基于自动编码器的结构，例如将resnet与自动编码器结合起来，也可能会带来对现有结构的改进。

VII. CONCLUSION

In this paper, we propose a convolutional autoencoder structure that is able to automatically design communication physical layer scheme according to different channel status. The system has no restriction on the length of input bit sequence. We conduct massive experiment to give empirical evidence for the superiority of the proposed system. The neural network has lower time complexity and higher accuracy especially for fading channel, and is also quite robust to channel variation. The framework can also be extended to OFDM system which transmits in frequency domain.

本文提出一种卷积自动编码器结构，能够根据不同的信道状态自动设计通信物理层方案。该系统对输入位序列的长度没有限制。我们进行了大量的实验，为所提出的系统的优越性提供了实证。该神经网络具有较低的时间复杂度和较高的精度，特别是对于衰落信道，对信道变化也具有相当的鲁棒性。该框架还可以扩展到频域传输的OFDM系统。

There is still a lot of work to be done in combining machine learning techniques with communication PHY. We may further explore the feasibility and utility of neural network based communication methods in following aspects.

在机器学习技术与通信PHY的结合上，还有很多工作要做。我们可以从以下几个方面进一步探讨基于神经网络的通信方法的可行性和实用性。

• One of the most important goals of designing a communication system is to maximize the capacity, i.e. the mutual information between input and output. However, since the constellation diagram in neural network based system is continuously distributed in the complex plane. It is hard for us to estimate the mutual information accurately, let alone optimizing the mutual information within neural network. A framework for analyzing mutual information in neural network based communication system may significantly enlarge our knowledge about both neural network and communication system. 
• An iterative, soft-input soft-output receiver can significantly improve the BER performance. Designing a receiver with both log likelihood ratio and received symbol as input using neural network may also enable iteration inside receiver, thus improving the current performance.
• The performance of neural network is still not as good in high SNR regime. It is important to figure out how autoencoder can learn a communication physical layer that outperforms existing communication techniques even in the high-SNR regions.
• 设计一个通信系统最重要的目标之一是最大限度地提高容量，即输入和输出之间的相互信息。然而，由于基于神经网络的系统中的星座图是连续分布在复杂平面上的。我们很难准确地估计互信息，更不用说优化神经网络内部的互信息了。一个基于神经网络的通信系统中的互信息分析框架，可能会大大扩展我们对神经网络和通信系统的认识。
• 迭代的软输入软输出接收机可以显著提高误码率性能。利用神经网络设计一个同时以对数似然比和接收符号为输入的接收机，也可以实现接收机内部的迭代，从而改善目前的性能。
• 在高SNR体制下，神经网络的性能还是不尽如人意。重要的是要弄清楚自动编码器如何学习一个通信物理层，即使在高SNR区域也能优于现有的通信技术。