Transformer-XL 模型详解

  本内容主要介绍 Transformer-XL 模型 架构。

1.1 Vanilla Transformer

  为了将 Transformer 或自注意力应用到语言模型中，面临的最大问题是：Transformer 如何将任意长的上下文编码为一个固定大小的表示。如果给定无限的内存和计算力，一个简单的解决方案是使用无条件的 Transformer 解码器处理整个上下文序列，类似于前馈神经网络。然而，在实践中，由于资源有限，这通常是不可行的。

  AI-Rfou 等人在 2018 年提出了一个可行单粗糙的近似方法：将整个语料库分割成可管理的较短片段，只在每个片段中训练模型，忽略前面片段中的所有上下文信息。将其称之为 Vanilla Transformer（即参考文档中的 [2]），如图 1.1a 所示。

图 1.1 片段长度为 4 的 Vanilla Transformer 模型

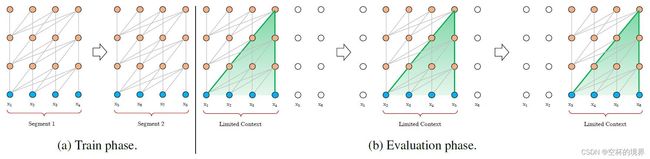
  该模型，在训练过程中，信息无法在片段见流动。使用固定长度的上下文，存在两个关键限值：

• 算法无法对超过固定长度的依赖关系建模。
• 将语料库分割成片段时，通常不遵循句子边界，从而造成上下文碎片（Context Fragmentation）问题。

  该模型，在评估过程中，每一步，Vanilla Transformer 模型也使用和训练阶段相同长度的片段，但是仅对最后一个位置进行预测。然后，在下一步，片段向右平移一个位置，再重头开始处理这个新片段。如图 1.1b 所示，该过程确保每一次利用训练阶段的最长的上下文进行预测，同时缓解了训练阶段的上下文碎片问题。然而，该过程的代价是极其昂贵的。

1.2 片段级的循环（Segment-Level Recurrence with State Reuse）

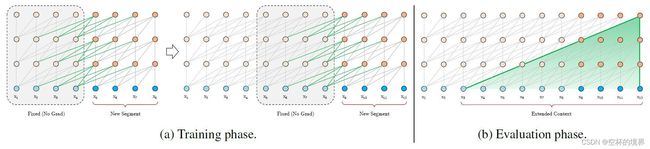
  为了解决固定长度上下文的限制，将循环机制引入到 Transformer 架构中。在训练过程中，为之前的片段计算的隐藏状态序列是固定的，将其缓存起来，并在模型处理后面的新片段时作为扩展上下文进行复用，如图 1.2a 所示。额外的输入允许网络利用历史中的信息，从而能够建模长期依赖关系并避免上下文碎片问题。

图 1.2 片段长度为 4 的 Transformer-XL 模型

  两个连续的长度为 $L$ 的片段表示为 ${\mathbf{s}}_{\tau }=[x_{\tau ,1},\cdots ,{\tau }_{\tau ,L}]$ 和 ${\mathbf{s}}_{\tau +1}=[x_{\tau +1,1},\cdots ,x_{\tau +1,L}]$。片段 ${\mathbf{s}}_{\tau }$ 的第 $n$ 层隐藏状态序列表示为 ${\mathbf{h}}_{\tau }^h\in {\mathbb{R}}^{L\times d}$，其中 $d$ 是隐层节点维度。${\mathbf{s}}_{\tau +1}$ 的第 $n$ 层隐藏状态 ${\mathbf{h}}_{\tau +1}^n$ 的计算方法如下：

$$\begin{array}{rl}{\mathbf{h}}_{\tau +1}^{n-1}& =[\text{SG}({\mathbf{h}}_{\tau }^{n-1})\circ {\mathbf{h}}_{\tau +1}^{n-1}]\\ {\mathbf{q}}_{\tau +1}^n,{\mathbf{k}}_{\tau +1}^n,{\mathbf{v}}_{\tau +1}^n& ={\mathbf{h}}_{\tau +1}^{n-1}{\mathbf{W}}_q^{\top },{\mathbf{h}}_{\tau +1}^{n-1}{\mathbf{W}}_k^{\top },{\mathbf{h}}_{\tau +1}^{n-1}{\mathbf{W}}_v^{\top }\\ {\mathbf{h}}_{\tau +1}^n& =\text{Transformer-Layer}({\mathbf{q}}_{\tau +1}^n,{\mathbf{k}}_{\tau +1}^n,{\mathbf{v}}_{\tau +1}^n)\end{array}\text{\hspace{1em}(1.1)}$$

其中，函数 $\text{SG}(\cdot )$ 表示 stop gradient，即不参与 BP（反向传播）的计算，符号 $[{\mathbf{h}}_u\circ {\mathbf{h}}_v]$ 表示两个隐藏状态序列在长度维度进行拼接，$\mathbf{W}$ 是模型需要学习的参数。与标准的 Transformer 相比，其主要区别在于 ${\mathbf{k}}_{\tau +1}^n$ 和 ${\mathbf{v}}_{\tau +1}^n$ 的值是通过 ${\mathbf{h}}_{\tau +1}^{n-1}$ 计算得到，${\mathbf{h}}_{\tau +1}^{n-1}$ 中包含了前一个片段的隐层状态 ${\mathbf{h}}_{\tau }^{n-1}$。

  这种循环机制应用于语料库中的每两个连续片段，本质上相当于在隐藏状态创建片段级的循环。因此，利用的有效上下文可以远远超出两个片段。请注意，${\mathbf{h}}_{\tau +1}^n$ 和 ${\mathbf{h}}_{\tau }^{n-1}$ 之间的循环依赖是每段向下移动一层（即片段 ${\mathbf{s}}_{\tau +1}$ 的第 $n$ 层隐藏状态 ${\mathbf{h}}_{\tau +1}^n$ 是依赖前一个片段 ${\mathbf{s}}_{\tau }$ 的第 $n-1$ 层隐藏状态 ${\mathbf{h}}_{\tau }^{n-1}$。），这与传统的 RNN-LMs 中的同一层循环不同。因此，最大可能的依赖项长度随层数和段长度呈线性增长，即 $O(N\times L)$，如图 1.2b 中阴影区域所示。

  除了实现超长上下文依赖和解决上下文碎片问题外，循环方案的另一个好处是大大加快了推理速度。在进行推理时，Vanilla Transformer 模型每次只能前进一个时间片，而 Transformer-XL 通过直接复用前一个片段的表示，从而实现推理速度的提升。

  最后，请注意，此循环方案不需要仅限于前一片段。理论上，我们可以在 GPU 内存允许的范围内缓存尽可能多的以前的片段，并在处理当前片段时将它们作为额外上下文进行复用。

1.3 相对位置编码（Relative Positional Encodings）

  尽管在上一小节中提出的想法极具吸引力，但为了重复使用隐藏状态，我们还有一个尚未解决的重要技术问题。那就是，当我们重复使用隐藏状态时，要如何保证位置信息的一致性呢？

  在标准的 Transformer 中，序列的顺序信息是通过一个位置编码集合 $\mathbf{U}\in {\mathbb{R}}^{L_{max}\times d}$ 提供的，其中第 $i$ 行 ${\mathbb{U}}_i$ 表示片段中第 $i$ 个绝对位置，$L_{max}$ 表示建模的最大长度。然后，Transformer 的输入是由词嵌入和位置编码相加得到。如果我们简单的将这种位置编码运用到上面的循环机制中，隐藏状态序列的计算如下：

$$\begin{array}{rl}{h}_{\tau +1}& =f(h_{\tau },{\mathbf{E}}_{s_{\tau +1}}+{\mathbf{U}}_{1:L})\\ h_{\tau }& =f(h_{\tau -1},{\mathbf{E}}_{s_{\tau }}+{\mathbf{U}}_{1:L})\end{array}\text{\hspace{1em}(1.2)}$$

其中，${\mathbf{E}}_{s_{\tau }}\in {\mathbb{R}}^{L\times d}$ 是序列 $s_{\tau }$ 的词嵌入，$f$ 表示转换函数。注意，${\mathbf{E}}_{s_{\tau }}$ 和 ${\mathbf{E}}_{s_{\tau +1}}$ 使用了相同的位置编码 ${\mathbf{U}}_{1:L}$。因此，对于任意的 $j=1,2,\cdots ,L$，模型无法分辨 $x_{\tau ,j}$ 和 $x_{\tau +1,j}$ 位置的区别，从而造成性能损失。

  为了避免上述的问题，最简单的方法是在隐藏状态中仅编码相对位置信息。从概念上来说，位置编码为模型提供了关于如何收集信息的时间线索，即关注哪里。出于同样的目的，可以在每一层中将类似的信息加入到注意力分数中。更重要的是，以相对位置定义时序偏差是更直观和普遍。

  在经典相对位置编码的基础上，作者提出了一种新的相对位置编码。

  在标准 Transformer 中，query 向量 $q_i$ 和 key 向量 $k_j$ 的注意力分的公式如下：

$${\mathbf{A}}_{i,j}^{abs}=\frac{({\mathbf{W}}_q({\mathbf{E}}_{x_i}+{\mathbf{U}}_i){)}^{\top }({\mathbf{W}}_k({\mathbf{E}}_{x_j}+{\mathbf{U}}_j))}{\sqrt{d}}\text{\hspace{1em}(1.3)}$$

  首先，将式（1.3）展开（在这里，我们不考虑分母的 $\sqrt{d}$，因为其对分析结果不会产生影响），得到：

$$\begin{array}{rl}{\mathbf{A}}_{i,j}^{abs}=& \underset{(a)}{{\mathbf{E}}_{x_i}^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_k{\mathbf{E}}_{x_j}}+\underset{(b)}{{\mathbf{E}}_{x_i}^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_k{\mathbf{U}}_j}\\ & +\underset{(c)}{{\mathbf{U}}_i^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_k{\mathbf{E}}_{x_j}}+\underset{(d)}{{\mathbf{U}}_i^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_k{\mathbf{U}}_j}\end{array}\text{\hspace{1em}(1.4)}$$

  然后，对上式做一些变化，得到：

$$\begin{array}{rl}{\mathbf{A}}_{i,j}^{abs}=& \underset{(a)}{{\mathbf{E}}_{x_i}^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_{k,E}{\mathbf{E}}_{x_j}}+\underset{(b)}{{\mathbf{E}}_{x_i}^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_{k,R}{\mathbf{R}}_{i-j}}\\ & +\underset{(c)}{u^{\top }{\mathbf{W}}_{k,E}{\mathbf{E}}_{x_j}}+\underset{(d)}{v^{\top }{\mathbf{W}}_{k,R}{\mathbf{R}}_{i-j}}\end{array}\text{\hspace{1em}(1.5)}$$

• 首先，是（b）和（d）中的绝对位置编码 $p_j$ 被换成相对位置编码 ${\mathbf{R}}_{i-j}$，其中 $\mathbf{R}$ 采用了 标准 Transformer 中不需要训练的 sinusoid 编码矩阵。
• 第二，引入两个可学习的参数 $u$ 和 $v$ 来分别替换（c）和（d）中的 ${\mathbf{U}}_i^{\top }{\mathbf{W}}_q^{\top }$。因为对所有的查询位置，查询向量是一样；即无论查询位置如何，对不同词的注意力偏置应保持一致。
• 最后，将 ${\mathbf{W}}_k$ 拆分为两个权重矩阵 ${\mathbf{W}}_{k,E}$ 和 ${\mathbf{W}}_{k,R}$，即分别为基于内容的 key 向量和基于位置的 key 向量。

  通过修改之后，式（1.5）中每个部分都有了其含义：（a）项表示基于内容的寻址（没有考虑位置编码）；（b）项表示相对于内容的位置偏差；（c）项表示全局的内容偏置（从内容层面衡量键的重要性）；（d）项表示全局的位置偏差（从相对位置层面衡量键的重要性）。

  综合上面提到的循环机制和相对位置编码，最终得到 Transformer-XL 架构。Transformer-XL 中的第 $N$ 层的单注意力头计算过程如下：

$$\begin{array}{rl}{\mathbf{h}}_{\tau }^{n-1}& =[\text{SG}({\mathbf{m}}_{\tau }^{n-1})\circ {\mathbf{h}}_{\tau }^{n-1}]\\ {\mathbf{q}}_{\tau }^n,{\mathbf{k}}_{\tau }^n,{\mathbf{v}}_{\tau }^n& ={\mathbf{h}}_{\tau }^{n-1}{{\mathbf{W}}_q^n}^{\top },{\mathbf{h}}_{\tau }^{n-1}{{\mathbf{W}}_{k,E}^n}^{\top },{\mathbf{h}}_{\tau }^{n-1}{{\mathbf{W}}_v^n}^{\top }\\ {\mathbf{A}}_{\tau ,i,j}^n& ={{\mathbf{q}}_{\tau ,i}^n}^{\top }{\mathbf{k}}_{\tau ,j}^n+{{\mathbf{q}}_{\tau ,i}^n}^{\top }{\mathbf{W}}_{k,R}^n{\mathbf{R}}_{i-j}+u^{\top }{\mathbf{k}}_{\tau ,j}^n+v^{\top }{\mathbf{W}}_{k,R}^n{\mathbf{R}}_{i-j}\\ {\mathbf{a}}_{\tau }^n& =\text{Masked-Softmax}({\mathbf{A}}_{\tau }^n){\mathbf{v}}_{\tau }^n\\ {\mathbf{o}}_{\tau }^n& =\text{LayerNorm}(\text{Linear}({\mathbf{a}}_{\tau }^n)+{\mathbf{h}}_{\tau }^{n-1})\\ {\mathbf{h}}_{\tau }^n& =\text{Positionwise-Feed-Forward}({\mathbf{o}}_{\tau }^n)\end{array}\text{\hspace{1em}(1.6)}$$

初始化 ${\mathbf{h}}_{\tau }^0:={\mathbf{E}}_{{\mathbf{s}}_{\tau }}$，即词嵌入序列。

  总结：Transformer-XL 是为了进一步提升 Transformer 建模长期依赖的能力而出现的。它的核心算法包含两部分：片段循环机制（segment-level recurrence）和相对位置编码机制（Relative positional encoding）。Transformer-XL 带来的提升包括：（1）捕获长期依赖的能力；（2）解决了上下文碎片问题（context segmentation problem）；（3）提升模型的预测速度和准确度。

参考：

[1] Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context

[2] Character-Level Language Modeling with Deeper Self-Attention

[3] 微信公众号“谷歌开发者”——Transformer-XL：释放注意力模型的潜力

[4] 详解Transformer-XL

[5] 【论文阅读笔记】Transformer-XL

[6] 论文阅读 | Transformer-XL: Attentive Language Models beyond a Fixed-Length Context

[7] https://github.com/kimiyoung/transformer-xl