TensorFlow学习一 --- 线性回归

TensorFlow学习一 — 线性回归

一、了解回归问题

1.1什么是回归模型

回归模型是一种预测性的建模技术，它研究的是因变量（目标）和自变量（预测器）之间的关系。这种技术通常用于预测分析，时间序列模型以及发现变量之间的因果关系。例如，司机的鲁莽驾驶与道路交通事故数量之间的关系，最好的研究方法就是回归。

1.2回归应用场景

回归问题的应用场景一般是预测的结果是连续的。例如，预测明天的温度，23，24，25度
回归问题通常是用来预测一个值，如预测房价、未来的天气情况等等，例如一个产品的实际价格为500元，通过回归分析预测值为499元，我们认为这是一个比较好的回归分析。
一个比较常见的回归算法是线性回归算法（LR）。另外，回归分析用在神经网络上，其最上层是不需要加上softmax函数的，而是直接对前一层累加即可。回归是对真实值的一种逼近预测。

二、线性回归（LR）

英文全称（Linear Regression），线性回归原理通过使用最佳的拟合直线（又被称为回归线），建立因变量（Y）和一个或多个自变量（X）之间的关系。简单来说线性回归是指全部由线性变量组成的回归模型。

回归模型：
但在现实生活中一般是有一个随机噪声
= ∗ + + eps
例如下图，红色点为真实带有噪声数据，我们通过拟合拟合初我们想要的规律，例如，拟合出一元一次，或一元二次。

所谓拟合就是 ∗ + 更接近于真实值y，那么我们就引进一个概念损失函数也叫做误差函数，这次先试用MAE（均方误差）。

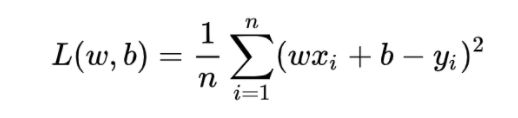
换句话来说就是将拟合数据改变为求Loss最小的问题了。什么时候Loss最小呢，我们一般采用两种方法，一种是最小二乘法，另一种就是梯度下降法。
least square method

Gradient Descent
梯度下降核心内容是对自变量进行不断的更新（针对w和b求偏导），使得目标函数不断逼近最小值的过程，lr为学习率。


例子：完整代码链接
定义损失函数：用MSE
numpy:

def compute_error_for_line_given_points(b, w, points):
    totalError = 0
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        # MSE
        totalError += (y - (w * x + b)) ** 2
    # average loss for each point

    return totalError / float(len(points))

或者使用TensorFlow

def compute_error_for_line_given_points(b, w, points):
    totalError = 0
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        # MSE
        loss = tf.reduce_mean(tf.square(y - (w * x + b))
    return loss

numpy求偏导

def step_gradient(b_current, w_current, points, learningRate):
    b_gradient = 0
    w_gradient = 0
    N = float(len(points))
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        # grad_b = 2(wx+b-y)
        b_gradient += (2 / N) * ((w_current * x + b_current) - y)
        # grad_w = 2(wx+b-y)*x
        w_gradient += (2 / N) * x * ((w_current * x + b_current) - y)
    # update w'
    new_b = b_current - (learningRate * b_gradient)
    new_w = w_current - (learningRate * w_gradient)
    return [new_b, new_w]

迭代函数

def gradient_descent_runner(points, starting_b, starting_w, learning_rate, num_iterations):
    b = starting_b
    w = starting_w
    # update for several times
    for i in range(num_iterations):
        b, w = step_gradient(b, w, np.array(points), learning_rate)
    return [b, w]

在主函数中设置好参数

    learning_rate = 0.0001
    initial_b = 0
    initial_w = 0
    num_iterations = 1000

运行后为：