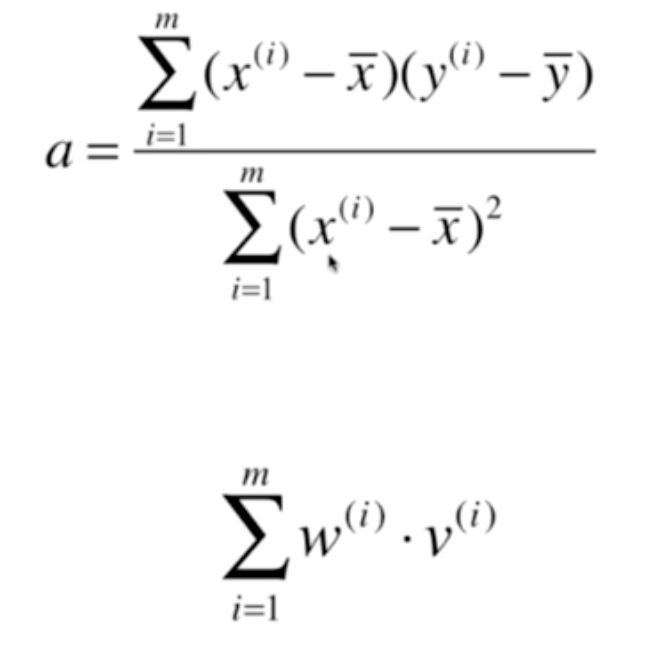__Miracle__

利用机器学习进行放假预测

爬虫能做什么

爬虫除了能够获取互联网的数据以外还能够帮我们完成很多繁琐的手动操作，这些操作不仅仅包括获取数据，还能够添加数据，比如：

投票
管理多个平台的多个账户(如各个电商平台的账号)
微信聊天机器人

实际的应用远不止上面这些，但是上面的应用只是除开数据本身的应用而已，数据本身的应用也是很广的：

机器学习语料库
垂直领域的服务(二手车估值)
聚合服务(去哪儿网,美团)
新闻推荐(今日头条)
预测和判断(医疗领域)

所以爬虫能做的功能非常多，也就造就了爬虫的需求也是越来越旺盛，但是很多有过后端开发的人员却觉得爬虫很简单，很多人觉得爬虫用一个库(requests)去获取一个html然后解析就行了，实际上爬虫真的这么简单吗？

首先学习之前我们来问几个问题：

如果一个网页需要登录才能访问，怎么办?
对于上面的问题，很多人说模拟登录就行了，但实际上很多网站会采用各种手段去加大模拟登录的难度，如：各种验证码，登录逻辑的各种混淆和加密、参数的各种加密，这些问题都怎么解决？
很多网站只能手机登录怎么办？
很多网站为了用户体验和服务器优化，会将一个页面的各个元素采用异步加载或者js加载的方式完成？这些你有能力分析出来吗？
作为一个网站，各种反爬的方案也是层出不穷，当你的爬虫被反爬之后，你如何去猜测对方是怎么反爬的？
一个爬虫怎么发现最新的数据？如何发现一个数据是否被更新了？
如果你只是做一个简单的爬虫，比如你的爬虫就是一次性的，一次性获取某个网站的某些数据这样当然就简单了，但是你要做一个爬虫服务，你就必须要面对上面的问题，这上面还没有提到数据的提取和解析等等

爬虫之旅

新建本地html文件
首先新建打开pycharm新建static文件夹然后新建index.html


<html lang="en">
<head>
    <meta charset="UTF-8">
    <title>Titletitle>
head>
<body>
<h1>欢迎来到王者荣耀h1>
<ul>
    <li>
        <a href="https://pvp.qq.com/web201605/herodetail/112.shtml">鲁班七号a>
    li>
    <li><a href="#">赵云a>li>
    <li><a href="#">李白a>li>
    <li><a href="#">安琪拉a>li>
ul>

<p>不给我选鲁班我就送p>
<p>那好你选吧p>

<div id="container-bd">这是div标签div>
<div id="container">
    <p class="action-counter">文本内容1p>
    <p class="action-checkbox">文本内容2p>

    <a href="http://www.neusoft.com">点击跳转至东软官方网站a>
div>


<p class="action-counter">文本内容1p>

body>
html>

使用python读取本地html文件

with open(file='./static/index.html', mode='r', encoding='utf-8') as f:
    html_data = f.read()
print(html_data)

html_data变量中存放的就是html文件的所有源码

数据提取

获取了所有的HTML数据，接下来我们就要提取出来这些数据

非结构化的数据处理

文本、电话号码、邮箱地址

正则表达式

HTML 文件

正则表达式
XPath
CSS选择器

结构化的数据处理

JSON 文件

JSON Path
转化成Python类型进行操作（json类）

XML 文件

转化成Python类型（xmltodict）
XPath
CSS选择器
正则表达式

有同学说，我正则用的不好，处理HTML文档很累，有没有其他的方法？
有！那就是XPath，我们可以先将 HTML文件转换成 XML文档，然后用 XPath 查找 HTML 节点或元素。

使用xpath语法进行html的内容提取

XPath (XML Path Language) 是一门在 XML 文档中查找信息的语言，可用来在 XML 文档中对元素和属性进行遍历。

W3School官方文档：http://www.w3school.com.cn/xpath/index.asp
Xpath最常用语法：

其中 / 从根节点选取。 // 代表从匹配选择的当前节点选择文档中的节点，而不考虑它们的位置
XPath的语法内容，在运用到Python抓取时要先转换为xml

lxml

xml 是一个HTML/XML的解析器，主要的功能是如何解析和提取 HTML/XML 数据。
lxml和正则一样，也是用 C 实现的，是一款高性能的 Python HTML/XML 解析器，我们可以利用之前学习的XPath语法，来快速的定位特定元素以及节点信息。lxml python 官方文档：http://lxml.de/index.html需要安装C语言库，可使用 pip 安装：pip install lxml （或通过wheel方式安装）

from lxml import html
with open(file='./static/index.html', mode='r', encoding='utf-8') as f:
    html_data = f.read()
#print(html_data)
# 解析html，返回单个元素/文档
selector = html.fromstring(html_data)
# print(selector)

h1 = selector.xpath('/html/body/h1/text()')
print(h1[0])
# # // 从任意的位置开始
# # //标签名1[@属性= "属性值"]/标签名2[@属性="属性值"]/..../text()
# # 获取a 标签中的内容
a= selector.xpath('//div[@id="container"]/a/text()')
print(a[0])
# # 爬取a 标签的属性  链接地址  @属性名
link = selector.xpath('//div[@id="container"]/a/@href')
print(link[0])
# 爬取鲁班七号的链接
luban_link = selector.xpath('//ul/li[1]/a/@href')
print(luban_link[0])
# # 获取英雄列表
ul_list = selector.xpath('//ul/li/a')
# #len 是列表中的元素的个数
print(len(ul_list))
for li in ul_list:
    hero = li.xpath('text()')
    print(hero[0])

输出结果：

欢迎来到王者荣耀
点击跳转至东软官方网站
http://www.neusoft.com
https://pvp.qq.com/web201605/herodetail/112.shtml
4
鲁班七号
赵云
李白
安琪拉

Requests库的使用

虽然Python的标准库中 urllib 模块已经包含了平常我们使用的大多数功能，但是它的 API 使用起来让人感觉不太好，而 Requests 自称 “HTTP for Humans”，说明使用更简洁方便。

Requests 唯一的一个非转基因的 Python HTTP 库，人类可以安全享用：）

Requests 继承了urllib的所有特性。Requests支持HTTP连接保持和连接池，支持使用cookie保持会话，支持文件上传，支持自动确定响应内容的编码，支持国际化的 URL 和 POST 数据自动编码。

requests 的底层实现其实就是 urllib

Requests的文档非常完备，中文文档也相当不错。Requests能完全满足当前网络的需求，支持Python 2.6–3.5，而且能在PyPy下完美运行。

开源地址：https://github.com/kennethreitz/requests

中文文档 API： http://docs.python-requests.org/zh_CN/latest/index.html

安装方式: 利用 pip 安装

pip install requests

最基本的GET请求可以直接用get方法

import requests
response = requests.get("http://www.baidu.com/")
print(response )

结果

import requests
from lxml import html
from xpinyin import Pinyin


def parse(city):
    movie_list = []
    city_pinyin = Pinyin().get_pinyin(city, '')
    url = "https://movie.douban.com/cinema/later/{}/".format(city_pinyin)
    print(url)
    html_data = requests.get(url).text
    selector = html.fromstring(html_data)

    # 找到影片名的列表
    div_list = selector.xpath('//div[@id ="showing-soon"]/div')
    print(city + "即将上映的电影共" + str(len(div_list)) + "部：")
    # 进行循环
    for li in div_list:
        # 电影名
        movie_name = li.xpath('div[1]/h3/a/text()')[0]
        print(movie_name)
        link = li.xpath('div[1]/h3/a/@href')[0]
        date = li.xpath('div[1]/ul/li[1]/text()')[0]
        type = li.xpath('div[1]/ul/li[2]/text()')[0]
        area = li.xpath('div[1]/ul/li[3]/text()')[0]
        want_see_counts = li.xpath('div[1]/ul/li[4]/span/text()')[0]
        want_see_counts = want_see_counts.replace('人想看', '')
        movie_list.append({
            'movie_name': movie_name,
            'want_see_counts': want_see_counts,
            'date': date,
            'type': type,
            'area': area,
            'link': link,
        })

    movie_list = sorted(movie_list, key=lambda item: float(item["want_see_counts"]), reverse=True)
    print("电影依照收人们欢迎程度排序：")
    for movie in movie_list:
        print("片名"+ movie["movie_name"] + "  上映日期:" + movie["date"])
        print("关注者:" + movie["want_see_counts"] + "    类型:" + movie["type"] + "    链接:" + "  " + movie["link"])
        print("----------------------------------------------------------")

city = input("请输入想要了解的即将上映电影的城市：")
parse(city)

Numpy 和 Matplotlib 可视化数据结构

Matplotlib 是一个 Python 的 2D绘图库，它以各种硬拷贝格式和跨平台的交互式环境生成出版质量级别的图形。提供了一种有效的 MatLab 开源替代方案

绘制柱状图

from matplotlib import pyplot as plt
import string
from random import randint
# 绘制 bar
x = [string.ascii_uppercase[i] for i in range(5)]
print(x) # ['A', 'B', 'C', 'D', 'E']
y = [randint(10, 30) for _ in range(5)]
print(y)
# 绘制柱状图
plt.bar(x, y)
plt.show()

import requests
from lxml import html
import matplotlib.pyplot as plt
from xpinyin import Pinyin
import pandas as pd

plt.rcParams["font.sans-serif"] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def parse(city):
    movie_list = []
    city_pinyin = Pinyin().get_pinyin(city, '')
    url = "https://movie.douban.com/cinema/later/{}/".format(city_pinyin)
    print(url)
    html_data = requests.get(url).text
    selector = html.fromstring(html_data)

    # 找到影片名的列表
    div_list = selector.xpath('//div[@id ="showing-soon"]/div')
    print( city + "即将上映的电影共" + str(len(div_list)) + "部：")
    # 进行循环
    for li in div_list:
        # 电影名
        movie_name = li.xpath('div[1]/h3/a/text()')[0]
        print(movie_name)
        link = li.xpath('div[1]/h3/a/@href')[0]
        date = li.xpath('div[1]/ul/li[1]/text()')[0]
        type = li.xpath('div[1]/ul/li[2]/text()')[0]
        area = li.xpath('div[1]/ul/li[3]/text()')[0]
        want_see_counts = li.xpath('div[1]/ul/li[4]/span/text()')[0]
        want_see_counts = want_see_counts.replace('人想看', '')
        movie_list.append({
            'movie_name': movie_name,
            'want_see_counts': want_see_counts,
            'date': date,
            'type': type,
            'area': area,
            'link': link,
        })

    movie_list = sorted(movie_list, key=lambda item: float(item["want_see_counts"]), reverse=True)
    print("电影依照收人们欢迎程度排序：")
    for movie in movie_list:
        print("片名"+ movie["movie_name"] + "  上映日期:" + movie["date"])
        print("关注者:" + movie["want_see_counts"] + "    类型:" + movie["type"] + "    链接:" + "  " + movie["link"])
        print("----------------------------------------------------------")
    #绘制电影关注人数排布榜
    # i['name'] for i in all_movies_info 这个是Python的快捷方式，
    # 这一句的作用是从all_movies_info这个list里面依次取出每个元素，
    all_names = [i['movie_name'] for i in movie_list]
    all_people = [i['want_see_counts'] for i in movie_list]
    # map函数：遍历每个序列中的元素，然后对每个元素进行函数操作
    all_people = list(map(lambda x: float(x), all_people))
    plt.barh(all_names, all_people,color='b')
    # plt.xticks(rotation=45),
    plt.xlabel('电影名')
    plt.ylabel('关注人数')
    plt.title('电影关注者排行榜')
    plt.show()


    # 绘制电影类型占比图
    all_types = [i['type'] for i in movie_list]
    type_count = {}
    for each_types in all_types:
        # 把 爱情 / 奇幻 这种分成[爱情, 奇幻]
        type_list = each_types.split(' / ')
        for e_type in type_list:
            if e_type not in type_count:
                type_count[e_type] = 1
            else:
                type_count[e_type] += 1
    # print(type_count) # 检测是否数据归类成功
    # # 直接取出统计的类型名和数量并强制转换为list。
    labels = list(type_count.keys())
    plt.pie(type_count.values(),pctdistance=0.8, labels=labels, autopct='%1.1f%%')
    plt.title("上映类型占比")
    # plt.legend()
    plt.show()


    # 上映地区比例
    movie_area = [i['area'] for i in movie_list]
    areas_count = {}
    for area in movie_area:
        if area not in areas_count:
            areas_count[area] = 1
        else:
            areas_count[area] += 1
    # print(areas_count)  # 输出验证数据是否正确
    plt.bar(list(areas_count.keys()), list(areas_count.values()))
    plt.title('上映地区统计')
    plt.xlabel('国家')
    plt.ylabel('数量')
    plt.show()

    df = pd.DataFrame(movie_list)
    df.to_csv('dddd1.csv', encoding='ansi')

city = input("请输入想要了解的即将上映电影的城市：")
parse(city)

实战房产数据爬取

import requests
import threading
import pandas as pd
# from lxml import etree
from lxml import html
# 全部信息列表
count=list()

#生成1-10页url
def url_creat():
    #基础url
    url = 'https://qd.lianjia.com/ershoufang/pg{}/'
    #生成前10页url列表
    links=[url.format(i) for i in range(1,11)]
    return links

#对url进行解析
def url_parse(url):
    headers = {
        'Accept': 'text/html,application/xhtml+xml,application/xml;q=0.9,image/avif,image/webp,image/apng,*/*;q=0.8,application/signed-exchange;v=b3;q=0.9',
        'Accept-Encoding': 'gzip, deflate, br',
        'Accept-Language': 'zh-CN,zh;q=0.9',
        'Cache-Control': 'no-cache',
        'Connection': 'keep-alive',
        'Cookie': 'lianjia_uuid=7e346c7c-5eb3-45d9-8b4f-e7cf10e807ba; UM_distinctid=17a3c5c21243a-0c5b8471aaebf5-6373267-144000-17a3c5c21252dc; _smt_uid=60d40f65.47c601a8; _ga=GA1.2.992911268.1624510312; select_city=370200; lianjia_ssid=f47906f0-df1a-49e2-ad9b-648711b11434; CNZZDATA1253492431=1056289575-1626962724-https%253A%252F%252Fwww.baidu.com%252F%7C1626962724; CNZZDATA1254525948=1591837398-1626960171-https%253A%252F%252Fwww.baidu.com%252F%7C1626960171; CNZZDATA1255633284=1473915272-1626960625-https%253A%252F%252Fwww.baidu.com%252F%7C1626960625; CNZZDATA1255604082=1617573044-1626960658-https%253A%252F%252Fwww.baidu.com%252F%7C1626960658; _jzqa=1.4194666890570963500.1624510309.1624510309.1626962867.2; _jzqc=1; _jzqy=1.1624510309.1626962867.2.jzqsr=baidu|jzqct=%E9%93%BE%E5%AE%B6.jzqsr=baidu; _jzqckmp=1; _qzjc=1; sensorsdata2015jssdkcross=%7B%22distinct_id%22%3A%2217a3c5c23964c1-05089a8de73cbf-6373267-1327104-17a3c5c23978b3%22%2C%22%24device_id%22%3A%2217a3c5c23964c1-05089a8de73cbf-6373267-1327104-17a3c5c23978b3%22%2C%22props%22%3A%7B%22%24latest_traffic_source_type%22%3A%22%E8%87%AA%E7%84%B6%E6%90%9C%E7%B4%A2%E6%B5%81%E9%87%8F%22%2C%22%24latest_referrer%22%3A%22https%3A%2F%2Fwww.baidu.com%2Flink%22%2C%22%24latest_referrer_host%22%3A%22www.baidu.com%22%2C%22%24latest_search_keyword%22%3A%22%E6%9C%AA%E5%8F%96%E5%88%B0%E5%80%BC%22%2C%22%24latest_utm_source%22%3A%22baidu%22%2C%22%24latest_utm_medium%22%3A%22pinzhuan%22%2C%22%24latest_utm_campaign%22%3A%22wyyantai%22%2C%22%24latest_utm_content%22%3A%22biaotimiaoshu%22%2C%22%24latest_utm_term%22%3A%22biaoti%22%7D%7D; Hm_lvt_9152f8221cb6243a53c83b956842be8a=1624510327,1626962872; _gid=GA1.2.134344742.1626962875; Hm_lpvt_9152f8221cb6243a53c83b956842be8a=1626962889; _qzja=1.1642609541.1626962866646.1626962866646.1626962866647.1626962872770.1626962889355.0.0.0.3.1; _qzjb=1.1626962866646.3.0.0.0; _qzjto=3.1.0; _jzqb=1.3.10.1626962867.1; srcid=eyJ0Ijoie1wiZGF0YVwiOlwiNzQ3M2M3OWQyZTQwNGM5OGM1MDBjMmMxODk5NTBhOWRhNmEyNjhkM2I5ZjNlOTkxZTdiMDJjMTg0ZGUxNzI0NDQ5YmZmZGI1ZjZmMDRkYmE0MzVmNmNlNDIwY2RiM2YxZTUzZWViYmQwYmYzMDQ1NDcyMzYwZTQzOTg3MzJhYTRjMTg0YjNhYjBkMGMyZGVmOWZiYjdlZWQwMDcwNWFkZmI5NzA5MjM1NmQ1NDg0MzQ3NGIzYjkwY2IyYmEwMjA2NjBjMjI2OWRjNjFiNDE3ZDc1NGViNjhlMzIzZmI0MjFkNzU5ZGNlMzAzMDhlNDAzYzIzNjllYWFlMzYxZGYxYjNmZmVkNGMxYTk1MmQ3MGY2MmJhMTQ1NWI4ODIwNTE5ODI2Njg2MmVkZTk4OWZiMDhjNTJhNzE3OTBlNDFiZDQzZTlmNDNmOGRlMTFjYTAwYTRlZTZiZWY5MTZkMTcwN1wiLFwia2V5X2lkXCI6XCIxXCIsXCJzaWduXCI6XCI3ZjI1NWI1ZlwifSIsInIiOiJodHRwczovL3FkLmxpYW5qaWEuY29tL2Vyc2hvdWZhbmcvMTAzMTE2MDkzOTU5Lmh0bWwiLCJvcyI6IndlYiIsInYiOiIwLjEifQ==',
        'Host': 'qd.lianjia.com',
        'Pragma': 'no-cache',
        'Referer': 'https://qd.lianjia.com/',
        'sec-ch-ua': '" Not;A Brand";v="99", "Google Chrome";v="91", "Chromium";v="91"',
        'sec-ch-ua-mobile': '?0',
        'Sec-Fetch-Dest': 'document',
        'Sec-Fetch-Mode': 'navigate',
        'Sec-Fetch-Site': 'same-origin',
        'Sec-Fetch-User': '?1',
        'Upgrade-Insecure-Requests': '1',
        'User-Agent': 'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/91.0.4472.164 Safari/537.36'}
    response=requests.get(url=url,headers=headers).text
    # etree=html.HTML(response)
    tree=html.fromstring(response)
    #ul列表下的全部li标签
    li_List=tree.xpath("//*[@class='sellListContent']/li")
    #创建线程锁对象
    lock = threading.RLock()
    #上锁
    lock.acquire()
    for li in li_List:
        #标题
        title=li.xpath('./div/div/a/text()')[0]
        #网址
        link=li.xpath('./div/div/a/@href')[0]
        #位置
        postion=li.xpath('./div/div[2]/div/a/text()')[0]+li.xpath('./div/div[2]/div/a[2]/text()')[0]
        #类型
        types=li.xpath('./div/div[3]/div/text()')[0].split(' | ')[0]
        #面积
        area=li.xpath('./div/div[3]/div/text()')[0].split(' | ')[1]
        #房屋信息
        info=li.xpath('./div/div[3]/div/text()')[0].split(' | ')[2:-1]
        info=''.join(info)
        #总价
        count_price=li.xpath('.//div/div[6]/div/span/text()')[0]+'万'
        #单价
        angle_price=li.xpath('.//div/div[6]/div[2]/span/text()')[0]
        dic={'标题':title,"位置":postion,'房屋类型':types,'面积':area,"单价":angle_price,'总价':count_price,'介绍':info,"网址":link}
        print(dic)
        #将房屋信息加入总列表中
        count.append(dic)
    #解锁
    lock.release()
def run():
    links = url_creat()
    #多线程爬取
    for i in links:
        x=threading.Thread(target=url_parse,args=(i,))
        x.start()
    x.join()
    #将全部房屋信息转化为excel
    data=pd.DataFrame(count)
    data.to_excel('房屋信息.xlsx',index=False)
if __name__ == '__main__':
    run()

线性回归算法简介

线性回归算法以一个坐标系里一个维度为结果，其他维度为特征（如二维平面坐标系中横轴为特征，纵轴为结果），无数的训练集放在坐标系中，发现他们是围绕着一条执行分布。线性回归算法的期望，就是寻找一条直线，最大程度的“拟合”样本特征和样本输出标记的关系

########## 样本特征只有一个的线性回归问题，为简单线性回归，如房屋价格-房屋面积

将横坐标作为x轴，纵坐标作为y轴，每一个点为（X(i) ,y(i)）,那么我们期望寻找的直线就是y=ax+b，当给出一个新的点x(j)的时候，我们希望预测的y^(j)=ax(j)+b

不使用直接相减的方式，由于差值有正有负，会抵消
不适用绝对值的方式，由于绝对值函数存在不可导的点

########## 通过上面的推导，我们可以归纳出一类机器学习算法的基本思路，如下图；其中损失函数是计算期望值和预测值的差值，期望其差值（也就是损失）越来越小，而效用函数则是描述拟合度，期望契合度越来越好

简单线性回归的最小二乘法推导过程

实现简单线性回归法

import numpy as np
import matplotlib.pyplot as plt

x = np.array([1., 2., 3., 4., 5.])
y = np.array([1., 3., 2., 3., 5.])

plt.scatter(x, y)
plt.axis([0, 6, 0, 6])
plt.show()

x_mean = np.mean(x)
y_mean = np.mean(y)

num = 0.0
d = 0.0
for x_i, y_i in zip(x, y):
    num += (x_i - x_mean) * (y_i - y_mean)
    d += (x_i - x_mean) ** 2

a = num/d

b = y_mean - a * x_mean

y_hat = a * x + b

plt.scatter(x, y)
plt.plot(x, y_hat, color='r')
plt.axis([0, 6, 0, 6])
plt.show()

x_predict = 6
y_predict = a * x_predict + b
y_predict

5.2000000000000002

封装我们自己的SimpleLinearRegression

代码SimpleLinearRegression.py

class SimpleLinearRegression1:

    def __init__(self):
        """初始化Simple Linear Regression 模型"""
        self.a_ = None
        self.b_ = None

    def fit(self, x_train, y_train):
        """根据训练集x_train，y_train 训练Simple Linear Regression 模型"""
        assert x_train.ndim == 1,\
            "Simple Linear Regression can only solve simple feature training data"
        assert len(x_train) == len(y_train),\
            "the size of x_train must be equal to the size of y_train"

        ## 求均值
        x_mean = x_train.mean()
        y_mean = y_train.mean()

        ## 分子
        num = 0.0
        ## 分母
        d = 0.0

        ## 计算分子分母
        for x_i, y_i in zip(x_train, y_train):
            num += (x_i-x_mean)*(y_i-y_mean)
            d += (x_i-x_mean) ** 2

        ## 计算参数a和b
        self.a_ = num/d
        self.b_ = y_mean - self.a_ * x_mean

        return self

    def predict(self, x_predict):
        """给定待预测集x_predict，返回x_predict对应的预测结果值"""
        assert x_predict.ndim == 1,\
            "Simple Linear Regression can only solve simple feature training data"
        assert self.a_ is not None and self.b_ is not None,\
            "must fit before predict!"

        return np.array([self._predict(x) for x in x_predict])

    def _predict(self, x_single):
        """给定单个待预测数据x_single，返回x_single对应的预测结果值"""
        return self.a_*x_single+self.b_

    def __repr__(self):
        return "SimpleLinearRegression1()"

from playML.SimpleLinearRegression import SimpleLinearRegression1

reg1 = SimpleLinearRegression1()
reg1.fit(x, y)
reg1.predict(np.array([x_predict]))

array([ 5.2])

reg1.a_

0.80000000000000004

reg1.b_

0.39999999999999947

y_hat1 = reg1.predict(x)

plt.scatter(x, y)
plt.plot(x, y_hat1, color='r')
plt.axis([0, 6, 0, 6])
plt.show()

向量化

向量化实现SimpleLinearRegression

代码SimpleLinearRegression.py

import numpy as np


class SimpleLinearRegression2:

    def __init__(self):
        """初始化Simple Linear Regression模型"""
        self.a_ = None
        self.b_ = None

    def fit(self, x_train, y_train):
        """根据训练数据集x_train,y_train训练Simple Linear Regression模型"""
        assert x_train.ndim == 1, \
            "Simple Linear Regressor can only solve single feature training data."
        assert len(x_train) == len(y_train), \
            "the size of x_train must be equal to the size of y_train"

        x_mean = np.mean(x_train)
        y_mean = np.mean(y_train)

        self.a_ = (x_train - x_mean).dot(y_train - y_mean) / (x_train - x_mean).dot(x_train - x_mean)
        self.b_ = y_mean - self.a_ * x_mean

        return self

    def predict(self, x_predict):
        """给定待预测数据集x_predict，返回表示x_predict的结果向量"""
        assert x_predict.ndim == 1, \
            "Simple Linear Regressor can only solve single feature training data."
        assert self.a_ is not None and self.b_ is not None, \
            "must fit before predict!"

        return np.array([self._predict(x) for x in x_predict])

    def _predict(self, x_single):
        """给定单个待预测数据x_single，返回x_single的预测结果值"""
        return self.a_ * x_single + self.b_

    def __repr__(self):
        return "SimpleLinearRegression2()"

from playML.SimpleLinearRegression import SimpleLinearRegression2

reg2 = SimpleLinearRegression2()
reg2.fit(x, y)
reg2.predict(np.array([x_predict]))

array([ 5.2])

reg2.a_

0.80000000000000004

reg2.b_

0.39999999999999947

向量化实现的性能测试

m = 1000000
big_x = np.random.random(size=m)
big_y = big_x * 2 + 3 + np.random.normal(size=m)
%timeit reg1.fit(big_x, big_y)
%timeit reg2.fit(big_x, big_y)

1 loop, best of 3: 984 ms per loop
100 loops, best of 3: 18.7 ms per loop

reg1.a_

1.9998479120324177

reg1.b_

2.9989427131166595

reg2.a_

1.9998479120324153

reg2.b_

2.9989427131166604

衡量线性回归算法的指标

衡量标准

其中衡量标准是和m有关的，因为越多的数据量产生的误差和可能会更大，但是毫无疑问越多的数据量训练出来的模型更好，为此需要一个取消误差的方法，如下

MSE 的缺点，量纲不准确，如果y的单位是万元，平方后就变成了万元的平方，这可能会给我们带来一些麻烦

RMSE 平方累加后再开根号，如果某些预测结果和真实结果相差非常大，那么RMSE的结果会相对变大，所以RMSE有放大误差的趋势，而MAE没有，他直接就反应的是预测结果和真实结果直接的差距，正因如此，从某种程度上来说，想办法我们让RMSE变的更小小对于我们来说比较有意义，因为这意味着整个样本的错误中，那个最值相对比较小，而且我们之前训练样本的目标，就是RMSE根号里面1/m的这一部分，而这一部分的本质和优化RMSE是一样的.

衡量回归算法的标准，MSE vs MAE

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

波士顿房产数据

boston = datasets.load_boston()

boston.keys()

dict_keys(['data', 'target', 'feature_names', 'DESCR'])

print(boston.DESCR)

    Boston House Prices dataset
    ===========================
    
    Notes
    ------
    Data Set Characteristics:  
    
        :Number of Instances: 506 
    
        :Number of Attributes: 13 numeric/categorical predictive
        
        :Median Value (attribute 14) is usually the target
    
        :Attribute Information (in order):
            - CRIM     per capita crime rate by town
            - ZN       proportion of residential land zoned for lots over 25,000 sq.ft.
            - INDUS    proportion of non-retail business acres per town
            - CHAS     Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
            - NOX      nitric oxides concentration (parts per 10 million)
            - RM       average number of rooms per dwelling
            - AGE      proportion of owner-occupied units built prior to 1940
            - DIS      weighted distances to five Boston employment centres
            - RAD      index of accessibility to radial highways
            - TAX      full-value property-tax rate per $10,000
            - PTRATIO  pupil-teacher ratio by town
            - B        1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
            - LSTAT    % lower status of the population
            - MEDV     Median value of owner-occupied homes in $1000's
    
        :Missing Attribute Values: None
    
        :Creator: Harrison, D. and Rubinfeld, D.L.
    
    This is a copy of UCI ML housing dataset.
    http://archive.ics.uci.edu/ml/datasets/Housing


    
    This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.
    
    The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic
    prices and the demand for clean air', J. Environ. Economics & Management,
    vol.5, 81-102, 1978.   Used in Belsley, Kuh & Welsch, 'Regression diagnostics
    ...', Wiley, 1980.   N.B. Various transformations are used in the table on
    pages 244-261 of the latter.
    
    The Boston house-price data has been used in many machine learning papers that address regression
    problems.   
         
    **References**
    
       - Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.
       - Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.
       - many more! (see http://archive.ics.uci.edu/ml/datasets/Housing)

boston.feature_names

array(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD',
       'TAX', 'PTRATIO', 'B', 'LSTAT'], 
      dtype='

 
  x = boston.data[:,5] ## 只使用房间数量这个特征
 
  x.shape
 
  (506,)
 
  y = boston.target
 
  y.shape
 
  (506,)
 
  plt.scatter(x, y)
plt.show()
 
   
  np.max(y)
 
  50.0
 
  x = x[y < 50.0]
y = y[y < 50.0]
 
  x.shape
 
  (490,)
 
  y.shape
 
  (490,)
 
  plt.scatter(x, y)
plt.show()
 
   
  使用简单线性回归法 
  from playML.model_selection import train_test_split

x_train, x_test, y_train, y_test = train_test_split(x, y, seed=666)
 
  x_train.shape
 
  (392,)
 
  y_train.shape
 
  (392,)
 
  x_test.shape
 
  (98,)
 
  y_test.shape
 
  (98,)
 
  from playML.SimpleLinearRegression import SimpleLinearRegression
 
  reg = SimpleLinearRegression()
reg.fit(x_train, y_train)
 
  SimpleLinearRegression()
 
  reg.a_
 
  7.8608543562689555
 
  reg.b_
 
  -27.459342806705543
 
  plt.scatter(x_train, y_train)
plt.plot(x_train, reg.predict(x_train), color='r')
plt.show()
 
   
  plt.scatter(x_train, y_train)
plt.scatter(x_test, y_test, color="c")
plt.plot(x_train, reg.predict(x_train), color='r')
plt.show()
 
   
  y_predict = reg.predict(x_test)
 
  MSE 
  mse_test = np.sum((y_predict - y_test)**2) / len(y_test)
mse_test
 
  24.156602134387438
 
  RMSE 
  from math import sqrt

rmse_test = sqrt(mse_test)
rmse_test
 
  4.914936635846635
 
  MAE 
  mae_test = np.sum(np.absolute(y_predict - y_test))/len(y_test)
mae_test
 
  3.5430974409463873
 
  封装我们自己的评测函数 
  代码: 
  import numpy as np
from math import sqrt


def accuracy_score(y_true, y_predict):
    """计算y_true和y_predict之间的准确率"""
    assert len(y_true) == len(y_predict), \
        "the size of y_true must be equal to the size of y_predict"

    return np.sum(y_true == y_predict) / len(y_true)


def mean_squared_error(y_true, y_predict):
    """计算y_true和y_predict之间的MSE"""
    assert len(y_true) == len(y_predict), \
        "the size of y_true must be equal to the size of y_predict"

    return np.sum((y_true - y_predict)**2) / len(y_true)


def root_mean_squared_error(y_true, y_predict):
    """计算y_true和y_predict之间的RMSE"""

    return sqrt(mean_squared_error(y_true, y_predict))


def mean_absolute_error(y_true, y_predict):
    """计算y_true和y_predict之间的MAE"""

    return np.sum(np.absolute(y_true - y_predict)) / len(y_true)
 
  from playML.metrics import mean_squared_error
from playML.metrics import root_mean_squared_error
from playML.metrics import mean_absolute_error
 
  mean_squared_error(y_test, y_predict)
 
  24.156602134387438
 
  root_mean_squared_error(y_test, y_predict)
 
  4.914936635846635
 
  mean_absolute_error(y_test, y_predict)
 
  3.5430974409463873
 
  scikit-learn中的MSE和MAE 
  from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
 
  mean_squared_error(y_test, y_predict)
 
  24.156602134387438
 
  mean_absolute_error(y_test, y_predict)
 
  3.5430974409463873
 
   
  最好的衡量线性回归法的指标 R Squared 
  RMSE 和 MAE的局限性 
   
  可能预测房源准确度，RMSE或者MAE的值为5，预测学生的分数，结果的误差是10，这个5和10没有判断性，因为5和10对应不同的单位和量纲，无法比较 
  解决办法-R Squared简介 
   
  R Squared 意义 
   
  使用BaseLine Model产生的错误会很大，使用我们的模型预测产生的错误会相对少些（因为我们的模型充分的考虑了y和x之间的关系），用这两者相减，结果就是拟合了我们的错误指标，用1减去这个商结果就是我们的模型没有产生错误的指标 
   
   
  实现 R Squared (R^2) 
  import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
 
  boston = datasets.load_boston()
x = boston.data[:,5] ## 只使用房间数量这个特征
y = boston.target

x = x[y < 50.0]
y = y[y < 50.0]
 
  from playML.model_selection import train_test_split

x_train, x_test, y_train, y_test = train_test_split(x, y, seed=666)
 
  from playML.SimpleLinearRegression import SimpleLinearRegression

reg = SimpleLinearRegression()
reg.fit(x_train, y_train)
 
  SimpleLinearRegression()
 
  reg.a_
 
  7.8608543562689555
 
  reg.b_
 
  -27.459342806705543
 
  y_predict = reg.predict(x_test)
 
  R Square 
  from playML.metrics import mean_squared_error

1 - mean_squared_error(y_test, y_predict)/np.var(y_test)
 
  ---------------------------------------------------------------------------

NameError                                 Traceback (most recent call last)

 in ()
      1 from playML.metrics import mean_squared_error
      2 
----> 3 1 - mean_squared_error(y_test, y_predict)/np.var(y_test)


NameError: name 'y_test' is not defined
 
  封装我们自己的 R Score 
  代码(playML/metrics.py) 
  def r2_score(y_true, y_predict):
    """计算y_true和y_predict之间的R Square"""

    return 1 - mean_squared_error(y_true, y_predict)/np.var(y_true)
 
  from playML.metrics import r2_score

r2_score(y_test, y_predict)
 
  0.61293168039373225
 
  scikit-learn中的 r2_score 
  from sklearn.metrics import r2_score

r2_score(y_test, y_predict)
 
  0.61293168039373236
 
  scikit-learn中的LinearRegression中的score返回r2_score:http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html 
  在我们的SimpleRegression中添加score 
  import numpy as np
from .metrics import r2_score


class SimpleLinearRegression:

 

    def score(self, x_test, y_test):
        """根据测试数据集 x_test 和 y_test 确定当前模型的准确度"""

        y_predict = self.predict(x_test)
        return r2_score(y_test, y_predict)



 
  reg.score(x_test, y_test)
 
  0.61293168039373225
 
   
  多元线性回归 
  多元线性回归简介和正规方程解 
   
   
   
   
  补充（矩阵点乘：A（m行）·B（n列） = A的每一行与B的每一列相乘再相加，等到结果是m行n列的） 
   
  补充（一个1xm的行向量乘以一个mx1的列向量等于一个数） 
   
  多元线性回归公式推导过程 
  ######## 基础知识
 
 
 
 
 ######## 多元线性回归公式推导过程
 
  
  多元线性回归实现 
   
  实现我们自己的 Linear Regression 
  import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
 
  boston = datasets.load_boston()

X = boston.data
y = boston.target

X = X[y < 50.0]
y = y[y < 50.0]
 
  X.shape
 
  (490, 13)
 
  from playML.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, seed=666)
 
  使用我们自己制作 Linear Regression 
  代码playML/LinearRegression.py 
  import numpy as np
from .metrics import r2_score


class LinearRegression:

    def __init__(self):
        """初始化Linear Regression模型"""

        ## 系数向量（θ1,θ2,.....θn）
        self.coef_ = None
        ## 截距 (θ0)
        self.interception_ = None
        ## θ向量
        self._theta = None

    def fit_normal(self, X_train, y_train):
        """根据训练数据集X_train，y_train 训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"

        ## np.ones((len(X_train), 1)) 构造一个和X_train 同样行数的，只有一列的全是1的矩阵
        ## np.hstack 拼接矩阵
        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        ## X_b.T 获取矩阵的转置
        ## np.linalg.inv() 获取矩阵的逆
        ## dot() 矩阵点乘
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)

        self.interception_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def predict(self, X_predict):
        """给定待预测数据集X_predict，返回表示X_predict的结果向量"""
        assert self.coef_ is not None and self.interception_ is not None,\
            "must fit before predict"
        assert X_predict.shape[1] == len(self.coef_),\
            "the feature number of X_predict must be equal to X_train"

        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        return X_b.dot(self._theta)

    def score(self, X_test, y_test):
        """根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""

        y_predict = self.predict(X_test)
        return r2_score(y_test, y_predict)

    def __repr__(self):
        return "LinearRegression()"

 
  from playML.LinearRegression import LinearRegression

reg = LinearRegression()
reg.fit_normal(X_train, y_train)
 
  LinearRegression()
 
  reg.coef_
 
  array([ -1.18919477e-01,   3.63991462e-02,  -3.56494193e-02,
         5.66737830e-02,  -1.16195486e+01,   3.42022185e+00,
        -2.31470282e-02,  -1.19509560e+00,   2.59339091e-01,
        -1.40112724e-02,  -8.36521175e-01,   7.92283639e-03,
        -3.81966137e-01])
 
  reg.intercept_
 
  34.161435496224712
 
  reg.score(X_test, y_test)
 
  0.81298026026584658
 
   
  09 scikit-learn中的回归问题 
  import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
 
  boston = datasets.load_boston()

X = boston.data
y = boston.target

X = X[y < 50.0]
y = y[y < 50.0]
 
  X.shape
 
  (490, 13)
 
  from playML.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, seed=666)
 
  scikit-learn中的线性回归 
  from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
 
  LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
 
  lin_reg.coef_
 
  array([ -1.18919477e-01,   3.63991462e-02,  -3.56494193e-02,
         5.66737830e-02,  -1.16195486e+01,   3.42022185e+00,
        -2.31470282e-02,  -1.19509560e+00,   2.59339091e-01,
        -1.40112724e-02,  -8.36521175e-01,   7.92283639e-03,
        -3.81966137e-01])
 
  lin_reg.intercept_
 
  34.161435496246924
 
  lin_reg.score(X_test, y_test)
 
  0.81298026026584758
 
  kNN Regressor 
  from sklearn.preprocessing import StandardScaler

standardScaler = StandardScaler()
standardScaler.fit(X_train, y_train)
X_train_standard = standardScaler.transform(X_train)
X_test_standard = standardScaler.transform(X_test)
 
  from sklearn.neighbors import KNeighborsRegressor

knn_reg = KNeighborsRegressor()
knn_reg.fit(X_train_standard, y_train)
knn_reg.score(X_test_standard, y_test)
 
  0.84664511530389497
 
  from sklearn.model_selection import GridSearchCV

param_grid = [
    {
        "weights": ["uniform"],
        "n_neighbors": [i for i in range(1, 11)]
    },
    {
        "weights": ["distance"],
        "n_neighbors": [i for i in range(1, 11)],
        "p": [i for i in range(1,6)]
    }
]

knn_reg = KNeighborsRegressor()
grid_search = GridSearchCV(knn_reg, param_grid, n_jobs=-1, verbose=1)
grid_search.fit(X_train_standard, y_train)
 
  Fitting 3 folds for each of 60 candidates, totalling 180 fits


[Parallel(n_jobs=-1)]: Done 180 out of 180 | elapsed:    1.5s finished





GridSearchCV(cv=None, error_score='raise',
       estimator=KNeighborsRegressor(algorithm='auto', leaf_size=30, metric='minkowski',
          metric_params=None, n_jobs=1, n_neighbors=5, p=2,
          weights='uniform'),
       fit_params={}, iid=True, n_jobs=-1,
       param_grid=[{'weights': ['uniform'], 'n_neighbors': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]}, {'weights': ['distance'], 'n_neighbors': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10], 'p': [1, 2, 3, 4, 5]}],
       pre_dispatch='2*n_jobs', refit=True, return_train_score=True,
       scoring=None, verbose=1)
 
  grid_search.best_params_
 
  {'n_neighbors': 5, 'p': 1, 'weights': 'distance'}
 
  grid_search.best_score_
 
  0.79917999890996905
 
  grid_search.best_estimator_.score(X_test_standard, y_test)
 
  0.88099665099417701
 
   
  10 线性回归参数的可解释性 
  import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
 
  boston = datasets.load_boston()

X = boston.data
y = boston.target

X = X[y < 50.0]
y = y[y < 50.0]
 
  from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X, y)
 
  LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
 
  lin_reg.coef_
 
  array([ -1.05574295e-01,   3.52748549e-02,  -4.35179251e-02,
         4.55405227e-01,  -1.24268073e+01,   3.75411229e+00,
        -2.36116881e-02,  -1.21088069e+00,   2.50740082e-01,
        -1.37702943e-02,  -8.38888137e-01,   7.93577159e-03,
        -3.50952134e-01])
 
  np.argsort(lin_reg.coef_)
 
  array([ 4,  7, 10, 12,  0,  2,  6,  9, 11,  1,  8,  3,  5])
 
  boston.feature_names[np.argsort(lin_reg.coef_)]
 
  array(['NOX', 'DIS', 'PTRATIO', 'LSTAT', 'CRIM', 'INDUS', 'AGE', 'TAX',
       'B', 'ZN', 'RAD', 'CHAS', 'RM'], 
      dtype='
 
  print(boston.DESCR)
 
      Boston House Prices dataset
    ===========================
    
    Notes
    ------
    Data Set Characteristics:  
    
        :Number of Instances: 506 
    
        :Number of Attributes: 13 numeric/categorical predictive
        
        :Median Value (attribute 14) is usually the target
    
        :Attribute Information (in order):
            - CRIM     per capita crime rate by town
            - ZN       proportion of residential land zoned for lots over 25,000 sq.ft.
            - INDUS    proportion of non-retail business acres per town
            - CHAS     Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
            - NOX      nitric oxides concentration (parts per 10 million)
            - RM       average number of rooms per dwelling
            - AGE      proportion of owner-occupied units built prior to 1940
            - DIS      weighted distances to five Boston employment centres
            - RAD      index of accessibility to radial highways
            - TAX      full-value property-tax rate per $10,000
            - PTRATIO  pupil-teacher ratio by town
            - B        1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
            - LSTAT    % lower status of the population
            - MEDV     Median value of owner-occupied homes in $1000's
    
        :Missing Attribute Values: None
    
        :Creator: Harrison, D. and Rubinfeld, D.L.
    
    This is a copy of UCI ML housing dataset.
    http://archive.ics.uci.edu/ml/datasets/Housing


    
    This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.
    
    The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic
    prices and the demand for clean air', J. Environ. Economics & Management,
    vol.5, 81-102, 1978.   Used in Belsley, Kuh & Welsch, 'Regression diagnostics
    ...', Wiley, 1980.   N.B. Various transformations are used in the table on
    pages 244-261 of the latter.
    
    The Boston house-price data has been used in many machine learning papers that address regression
    problems.   
         
    **References**
    
       - Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.
       - Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.
       - many more! (see http://archive.ics.uci.edu/ml/datasets/Housing)


 
  RM对应的是房间数，是正相关最大的特征，也就是说房间数越多，房价越高，这是很合理的
 NOX对应的是一氧化氮浓度，也就是说一氧化氮浓度越低，房价越低，这也是非常合理的
 由此说明，我们的线性回归具有可解释性，我们可以在对研究一个模型的时候，可以先用线性回归模型看一下，然后根据感性的认识去直观的判断一下是否符合我们的语气 
  多项式回归简介 
   
   考虑下面的数据，虽然我们可以使用线性回归来拟合这些数据，但是这些数据更像是一条二次曲线,相应的方程是y=ax2+bx+c,这是式子虽然可以理解为二次方程，但是我们呢可以从另外一个角度来理解这个式子： 
   如果将x2理解为一个特征，将x理解为另外一个特征,换句话说，本来我们的样本只有一个特征x，现在我们把他看成有两个特征的一个数据集。多了一个特征x2，那么从这个角度来看，这个式子依旧是一个线性回归的式子，但是从x的角度来看，他就是一个二次的方程 
   
   
  以上这样的方式，就是所谓的多项式回归 
  相当于我们为样本多添加了一些特征，这些特征是原来样本的多项式项，增加了这些特征之后，我们们可以使用线性回归的思路更好的我们的数据 
  什么是多项式回归 
  import numpy as np 
import matplotlib.pyplot as plt
 
  x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
# 一元二次方程
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)
 
  plt.scatter(x, y)
plt.show()
 
   
  线性回归？ 
  from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X, y)
y_predict = lin_reg.predict(X)
 
  plt.scatter(x, y)
plt.plot(x, y_predict, color='r')
plt.show()
 
   
  很明显，我们用一跟直线来拟合一根有弧度的曲线，效果是不好的 
  解决方案， 添加一个特征 
  原来所有的数据都在X中，现在对X中每一个数据都进行平方，
 再将得到的数据集与原数据集进行拼接，
 在用新的数据集进行线性回归 
  X2 = np.hstack([X, X**2])
 
  X2.shape
 
  (100, 2)
 
  lin_reg2 = LinearRegression()
lin_reg2.fit(X2, y)
y_predict2 = lin_reg2.predict(X2)
 
  plt.scatter(x, y)
# 由于x是乱的，所以应该进行排序
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
plt.show()
 
   
  从上图可以看出，当我们添加了一个特征（原来特征的平方）之后，再从x的维度来看，就形成了一条曲线，显然这个曲线对原来数据集的拟合程度是更好的 
  # 第一个系数是x前面的系数，第二个系数是x平方前面的系数
lin_reg2.coef_
 
  array([ 0.99870163,  0.54939125])
 
  lin_reg2.intercept_
 
  1.8855236786516001
 
  3.总结
 多线性回归在机器学习算法上并没有新的地方，完全是使用线性回归的思路
 他的关键在于为原来的样本，添加新的特征。而我们得到新的特征的方式是原有特征的多项式的组合。
 采用这样的方式，我们就可以解决一些非线性的问题 
  与此同时需要主要，我们在上一章所讲的PCA是对我们的数据进行降维处理，而我们这一章所讲的多项式回归显然在做一件相反的事情，他让我们的数据升维，在升维之后使得我们的算法可以更好的拟合高纬度的数据 
  scikit-learn中的多项式回归和Pipeline 
  import numpy as np 
import matplotlib.pyplot as plt
 
  x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)
 
  # sklearn中对数据进行预处理的函数都封装在preprocessing模块下，包括之前学的归一化StandardScaler
from sklearn.preprocessing import PolynomialFeatures
 
  poly = PolynomialFeatures(degree=2)  # 表示为数据的特征最多添加2次幂
poly.fit(X)
X2 = poly.transform(X)
 
  X2.shape
 
  (100, 3)
 
  X[:5,:]
 
  array([[ 0.14960154],
       [ 0.49319423],
       [-0.87176575],
       [-1.33024477],
       [ 0.47383199]])
 
  # 第一列是sklearn为我们添加的X的零次方的特征
# 第二列和原来的特征一样是X的一次方的特征
# 第三列是添加的X的二次方的特征
X2[:5,:]
 
  array([[ 1.        ,  0.14960154,  0.02238062],
       [ 1.        ,  0.49319423,  0.24324055],
       [ 1.        , -0.87176575,  0.75997552],
       [ 1.        , -1.33024477,  1.76955114],
       [ 1.        ,  0.47383199,  0.22451675]])
 
  from sklearn.linear_model import LinearRegression

lin_reg2 = LinearRegression()
lin_reg2.fit(X2, y)
y_predict2 = lin_reg2.predict(X2)
 
  plt.scatter(x, y)
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
plt.show()
 
   
  lin_reg2.coef_
 
  array([ 0.        ,  0.9460157 ,  0.50420543])
 
  lin_reg2.intercept_
 
  2.1536054095953823
 
  关于PolynomialFeatures 
  X = np.arange(1, 11).reshape(-1, 2)
 
  X
 
  array([[ 1,  2],
       [ 3,  4],
       [ 5,  6],
       [ 7,  8],
       [ 9, 10]])
 
  poly = PolynomialFeatures(degree=2)
poly.fit(X)
X2 = poly.transform(X)
 
  X2.shape
 
  (5, 6)
 
  X2
 
  array([[   1.,    1.,    2.,    1.,    2.,    4.],
       [   1.,    3.,    4.,    9.,   12.,   16.],
       [   1.,    5.,    6.,   25.,   30.,   36.],
       [   1.,    7.,    8.,   49.,   56.,   64.],
       [   1.,    9.,   10.,   81.,   90.,  100.]])
 
  将5行2列的矩阵进行多项式转换后变成了5行6列 
  第一列是1 对应的是0次幂
 第二列和第三列对应的是原来的x矩阵，此时他有两列一次幂的项
 第四列是原来数据的第一列平方的结果
 第六列是原来数据的第二列平方的结果
 第五列是原来数据的两列相乘的结果
 可以想象如果将degree设置为3，那么将产生一下10个元素 
   
  也就是说PolynomialFeatures会穷举出所有的多项式组合 
  Pipeline 
  pipline的英文名字是管道，那么 我们如何使用管道呢，先考虑我们多项式回归的过程 
  1.使用PolynomialFeatures生成多项式特征的数据集
 2.如果生成数据幂特别的大，那么特征直接的差距就会很大，导致我们的搜索非常慢，这时候可以进行数据归一化
 3.进行线性回归
 pipline 的作用就是把上面的三个步骤合并，使得我们不用一直重复这三步 
  x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
# 传入每一步的对象名和类的实例化
poly_reg = Pipeline([
    ("poly", PolynomialFeatures(degree=2)),
    ("std_scaler", StandardScaler()),
    ("lin_reg", LinearRegression())
])
 
  poly_reg.fit(X, y)
y_predict = poly_reg.predict(X)
 
  plt.scatter(x, y)
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
plt.show()
 
   
  过拟合和欠拟合 
  import numpy as np
import matplotlib.pyplot as plt
 
  np.random.seed(666)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)
 
  plt.scatter(x, y)
plt.show()
 
   
  使用线性回归 
  from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X, y)
lin_reg.score(X, y)
 
  0.49537078118650091
 
  y_predict = lin_reg.predict(X)
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
plt.show()
 
   
  使用均方误差来看拟合的结果，这是因为我们同样都是对一组数据进行拟合，所以使用不同的方法对数据进行拟合
 得到的均方误差的指标是具有可比性的。 
  from sklearn.metrics import mean_squared_error

y_predict = lin_reg.predict(X)
mean_squared_error(y, y_predict)
 
  3.0750025765636577
 
  使用多项式回归 
  from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler

def PolynomialRegression(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lin_reg", LinearRegression())
    ])
 
  poly2_reg = PolynomialRegression(degree=2)
poly2_reg.fit(X, y)
 
  Pipeline(steps=[('poly', PolynomialFeatures(degree=2, include_bias=True, interaction_only=False)), ('std_scaler', StandardScaler(copy=True, with_mean=True, with_std=True)), ('lin_reg', LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False))])
 
  y2_predict = poly2_reg.predict(X)
# 显然使用多项式回归得到的结果是更好的
mean_squared_error(y, y2_predict)
 
  1.0987392142417856
 
  plt.scatter(x, y)
plt.plot(np.sort(x), y2_predict[np.argsort(x)], color='r')
plt.show()
 
   
  poly10_reg = PolynomialRegression(degree=10)
poly10_reg.fit(X, y)

y10_predict = poly10_reg.predict(X)
mean_squared_error(y, y10_predict)
 
  1.0508466763764164
 
  plt.scatter(x, y)
plt.plot(np.sort(x), y10_predict[np.argsort(x)], color='r')
plt.show()
 
   
  poly100_reg = PolynomialRegression(degree=100)
poly100_reg.fit(X, y)

y100_predict = poly100_reg.predict(X)
mean_squared_error(y, y100_predict)
 
  0.68743577834336944
 
  plt.scatter(x, y)
plt.plot(np.sort(x), y100_predict[np.argsort(x)], color='r')
plt.show()
 
   
  这条曲线只是原来随机生成的点（分布不均匀）对应的y的预测值连接起来的曲线，不过有x轴很多地方可能没有数据点，所以连接的结果和原来的曲线不一样（不是真实的y曲线）。
 下面尝试真正还原原来的曲线（构造均匀分布的原数据集） 
  X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = poly100_reg.predict(X_plot)
 
  plt.scatter(x, y)
plt.plot(X_plot[:,0], y_plot, color='r')
plt.axis([-3, 3, 0, 10])  # 必须指定
plt.show()
 
   
  总有一条曲线，他能拟合所有的样本点，使得均方误差的值为0
 degree从2到10到100的过程中，虽然均方误差是越来越小的，从均方误差的角度来看是更加小的
 但是他真的能更好的预测我们数据的走势吗，例如我们选择2.5到3的一个x，使用上图预测出来的y的大小（0或者-1之间）显然不符合我们的数据 
  换句话说，我们使用了一个非常高维的数据，虽然使得我们的样本点获得了更小的误差，但是这根曲线完全不是我们想要的样子
 他为了拟合我们所有的样本点，变的太过复杂了，这种情况就是过拟合【over-fitting】 
  相反，在最开始，我们直接使用一根直线来拟合我们的数据，也没有很好的拟合我们的样本特征，当然他犯的错误不是太过复杂了，而是太过简单了
 这种情况，我们成为欠拟合-【under-fitting】 
  对于现在的数据（基于二次方程构造），我们使用低于2项的拟合结果，就是欠拟合；高于2项的拟合结果，就是过拟合 
  为什么要使用训练数据集和测试数据集 
  模型的泛化能力 
  使用上节的过拟合结果，我们可以得知，虽然我们训练出的曲线将原来的样本点拟合的非常好，总体的误差非常的小， 但是一旦来了新的样本点，他就不能很好的预测了，在这种情况下，我们就称我们得到的这条弯弯曲曲的曲线，他的**泛化能力（由此及彼的能力）**非常弱 
   
  image.png 
  训练数据集和测试数据集的意义 
  我们训练的模型目的是为了使得预测的数据能够尽肯能的准确，在这种情况下，我们观察训练数据集的拟合程度是没有意义的 我们真正需要的是，我们得到的模型的泛化能力更高，解决这个问题的方法也就是使用训练数据集，测试数据集的分离 
   
   
   测试数据对于我们的模型是全新的数据，如果使用训练数据获得的模型面对测试数据也能获得很好的结果，那么我们就说我们的模型泛化能力是很强的。 如果我们的模型面对测试数据结果很差的话，那么他的泛化能力就很弱。事实上，这是训练数据集更大的意义 
   
  train test split的意义 
  from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
 
  lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
y_predict = lin_reg.predict(X_test)
mean_squared_error(y_test, y_predict)
 
  2.2199965269396573
 
  poly2_reg = PolynomialRegression(degree=2)
poly2_reg.fit(X_train, y_train)
y2_predict = poly2_reg.predict(X_test)
mean_squared_error(y_test, y2_predict)
 
  0.80356410562978997
 
  poly10_reg = PolynomialRegression(degree=10)
poly10_reg.fit(X_train, y_train)
y10_predict = poly10_reg.predict(X_test)
mean_squared_error(y_test, y10_predict)
 
  0.92129307221507939
 
  poly100_reg = PolynomialRegression(degree=100)
poly100_reg.fit(X_train, y_train)
y100_predict = poly100_reg.predict(X_test)
mean_squared_error(y_test, y100_predict)
 
  14075796419.234262
 
  刚刚我们进行的实验实际上在实验模型的复杂度，对于多项式模型来说，我们回归的阶数越高，我们的模型会越复杂，在这种情况下对于我们的机器学习算法来说，通常是有下面一张图的。横轴是模型复杂度（对于不同的算法来说，代表的是不同的意思，比如对于多项式回归来说，是阶数越高，越复杂；对于KNN来说，是K越小，模型越复杂，k越大，模型最简单，当k=n的时候，模型就简化成了看整个样本里，哪种样本最多，当k=1来说，对于每一个点，都要找到离他最近的那个点），另一个维度是模型准确率（也就是他能够多好的预测我们的曲线） 
   
  通常对于这样一个图，会有两根曲线： 
   
   一个是对于训练数据集来说的，模型越复杂，模型准确率越高，因为模型越复杂，对训练数据集的拟合就越好，相应的模型准确率就越高 
   对于测试数据集来说，在模型很简单的时候，模型的准确率也比较低，随着模型逐渐变复杂，对测试数据集的准确率在逐渐的提升，提升到一定程度后，如果模型继续变复杂，那么我们的模型准确率将会进行下降（欠拟合->正合适->过拟合） 
   
  欠拟合和过拟合的标准定义 
   
   欠拟合：算法所训练的模型不能完整表述数据关系 过拟合：算法所训练的模型过多的表达了数据间的噪音关系 
   
  学习曲线 
  随着训练样本的逐渐增多，算法训练出的模型的表现能力 
  import numpy as np
import matplotlib.pyplot as plt
 
  np.random.seed(666)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)
 
  plt.scatter(x, y)
plt.show()
 
   
  学习曲线 
  实际编程实现学习曲线 
  from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=10)
 
  X_train.shape
 
  (75, 1)
 
  2.1观察线性回归的学习曲线：观察线性回归模型，随着训练数据集增加，性能的变化 
  from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

train_score = []
test_score = []
for i in range(1, 76):
    lin_reg = LinearRegression()
    lin_reg.fit(X_train[:i], y_train[:i])
    
    y_train_predict = lin_reg.predict(X_train[:i])
    train_score.append(mean_squared_error(y_train[:i], y_train_predict))
    
    y_test_predict = lin_reg.predict(X_test)
    test_score.append(mean_squared_error(y_test, y_test_predict))
 
  plt.plot([i for i in range(1, 76)], np.sqrt(train_score), label="train")
plt.plot([i for i in range(1, 76)], np.sqrt(test_score), label="test")
plt.legend()
plt.show()
 
   
  从趋势上看： 
  在训练数据集上，误差是逐渐升高的。这是因为我们的训练数据越来越多，我们的数据点越难得到全部的累积，不过整体而言，在刚开始的时候误差变化的比较快，后来就几乎不变了
 在测试数据集上，在使用非常少的样本进行训练的时候，刚开始我们的测试误差非常的大，当训练样本大到一定程度以后，我们的测试误差就会逐渐减小，减小到一定程度后，也不会小太多，达到一种相对稳定的情况
 在最终，测试误差和训练误差趋于相等，不过测试误差还是高于训练误差一些，这是因为，训练数据在数据非常多的情况下，可以将数据拟合的比较好，误差小一些，但是泛化到测试数据集的时候，还是有可能多一些误差 
  def plot_learning_curve(algo, X_train, X_test, y_train, y_test):
    train_score = []
    test_score = []
    for i in range(1, len(X_train)+1):
        algo.fit(X_train[:i], y_train[:i])
    
        y_train_predict = algo.predict(X_train[:i])
        train_score.append(mean_squared_error(y_train[:i], y_train_predict))
    
        y_test_predict = algo.predict(X_test)
        test_score.append(mean_squared_error(y_test, y_test_predict))
        
    plt.plot([i for i in range(1, len(X_train)+1)], 
                               np.sqrt(train_score), label="train")
    plt.plot([i for i in range(1, len(X_train)+1)], 
                               np.sqrt(test_score), label="test")
    plt.legend()
    plt.axis([0, len(X_train)+1, 0, 4])
    plt.show()
    
plot_learning_curve(LinearRegression(), X_train, X_test, y_train, y_test)
 
   
   
  from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline

def PolynomialRegression(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lin_reg", LinearRegression())
    ])

poly2_reg = PolynomialRegression(degree=2)
plot_learning_curve(poly2_reg, X_train, X_test, y_train, y_test)
 
   
  首先整体从趋势上，和线性回归的学习曲线是类似的
 仔细观察，和线性回归曲线的不同在于，线性回归的学习曲线1.5，1.8左右；2阶多项式回归稳定在了1.0，0.9左右,2阶多项式稳定的误差比较低，说明使用二阶线性回归的性能是比较好的 
  poly20_reg = PolynomialRegression(degree=20)
plot_learning_curve(poly20_reg, X_train, X_test, y_train, y_test)
 
  
 在使用20阶多项式回归训练模型的时候可以发现，在数据量偏多的时候，我们的训练数据集拟合的是比较好的，但是测试数据集的误差相对来说增大了很多，离训练数据集比较远，通常这就是过拟合的结果，他的泛化能力是不够的 
  总结 
   
  对于欠拟合比最佳的情况趋于稳定的那个位置要高一些，说明无论对于训练数据集还是测试数据集来说，误差都比较大。这是因为我们本身模型选的就不对，所以即使在训练数据集上，他的误差也是大的，所以才会呈现出这样的一种形态 
   
  对于过拟合的情况，在训练数据集上，他的误差不大，和最佳的情况是差不多的，甚至在极端情况，如果degree取更高的话，那么训练数据集的误差会更低，但是问题在于，测试数据集的误差相对是比较大的，并且训练数据集的误差和测试数据集的误差相差比较大（表现在图上相差比较远），这就说明了此时我们的模型的泛化能力不够好，他的泛化能力是不够的 
  验证数据集与交叉验证 
  使用分割训练数据集和测试数据集来判断我们的机器学习性能的好坏，虽然是一个非常好的方案，但是会产生一个问题：针对特定测试数据集过拟合 
  我们每次使用测试数据来分析性能的好坏。一旦发现结果不好，我们就换一个参数（可能是degree也可能是其他超参数）重新进行训练。这种情况下，我们的模型在一定程度上围绕着测试数据集打转。也就是说我们在寻找一组参数，使得这组参数训练出来的模型在测试结果集上表现的最好。但是由于这组测试数据集是已知的，我们相当于在针对这组测试数据集进行调参，那么他也有可能产生过拟合的情况，也就是我们得到的模型针对测试数据集过拟合了 
   
  那么怎么解决这个问题呢？ 解决的方式其实就是：我们需要将我们的问题分为三部分，这三部分分别是训练数据集，验证数据集，测试数据集。 我们使用训练数据集训练好模型之后，将验证数据集送给这个模型，看看这个训练数据集训练的效果是怎么样的，如果效果不好的话，我们重新换参数，重新训练模型。直到我们的模型针对验证数据来说已经达到最优了。 这样我们的模型达到最优以后，再讲测试数据集送给模型，这样才能作为衡量模型最终的性能。换句话说，我们的测试数据集是不参与模型的创建的，而其他两个数据集都参与了训练。但是我们的测试数据集对于模型是完全不可知的，相当于我们在模型这个模型完全不知道的数据 
   
  这种方法还会有一个问题。由于我们的模型可能会针对验证数据集过拟合，而我们只有一份验证数据集，一旦我们的数据集里有比较极端的情况，那么模型的性能就会下降很多，那么为了解决这个问题，就有了交叉验证。 
  交叉验证 Cross Validation 
  交叉验证相对来说是比较正规的、比较标准的在我们调整我们的模型参数的时候看我们的性能的方式 
  交叉验证：在训练模型的时候，通常把数据分成k份，例如分成3份（ABC）（分成k分，k属于超参数），这三份分别作为验证数据集和训练数据集。这样组合后可以分别产生三个模型，这三个模型，每个模型在测试数据集上都会产生一个性能的指标，这三个指标的平均值作为当前这个算法训练处的模型衡量的标准是怎样的。 由于我们有一个求平均的过程，所以不会由于一份验证数据集中有比较极端的数据而导致模型有过大的偏差，这比我们只分成训练、验证、测试数据集要更加准确 
   
  Validation 和 Cross Validation 
  import numpy as np
from sklearn import datasets
 
  digits = datasets.load_digits()
X = digits.data
y = digits.target
 
  测试train_test_split 
  from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=666)
 
  from sklearn.neighbors import KNeighborsClassifier

best_k, best_p, best_score = 0, 0, 0
# k为k近邻中的寻找k个最近元素
for k in range(2, 11):
# p为明科夫斯基距离的p
    for p in range(1, 6):
        knn_clf = KNeighborsClassifier(weights="distance", n_neighbors=k, p=p)
        knn_clf.fit(X_train, y_train)
        score = knn_clf.score(X_test, y_test)
        if score > best_score:
            best_k, best_p, best_score = k, p, score
            
print("Best K =", best_k)
print("Best P =", best_p)
print("Best Score =", best_score)
 
  Best K = 3
Best P = 4
Best Score = 0.986091794159
 
  使用交叉验证 
  # 使用sklearn提供的交叉验证
from sklearn.model_selection import cross_val_score

knn_clf = KNeighborsClassifier()
# 返回的是一个数组，有三个元素，说明cross_val_score方法默认将我们的数据集分成了三份
# 这三份数据集进行交叉验证后产生了这三个结果

# cv默认为3，可以修改改参数，修改修改不同分数的数据集
cross_val_score(knn_clf,X_train,y_train,cv=3)
 
  array([ 0.98895028,  0.97777778,  0.96629213])
 
  best_k, best_p, best_score = 0, 0, 0
for k in range(2, 11):
    for p in range(1, 6):
        knn_clf = KNeighborsClassifier(weights="distance", n_neighbors=k, p=p)
        scores = cross_val_score(knn_clf, X_train, y_train)
        score = np.mean(scores)
        if score > best_score:
            best_k, best_p, best_score = k, p, score
            
print("Best K =", best_k)
print("Best P =", best_p)
print("Best Score =", best_score)
 
  Best K = 2
Best P = 2
Best Score = 0.982359987401
 
  通过观察两组调参过程的结果可以发现
 1.两组调参得出的参数结果是不同的，通常这时候我们更愿意详细使用交叉验证的方式得出的结果。
 因为使用train_test_split很有可能只是过拟合了测试数据集得出的结果
 2.使用交叉验证得出的最好分数0.982是小于使用分割训练测试数据集得出的0.986，因为在交叉验证的
 过程中，通常不会过拟合某一组的测试数据，所以平均来讲这个分数会稍微低一些 
  但是使用交叉验证得到的最好参数Best_score并不是真正的最好的结果，我们使用这种方式只是为了拿到
 一组超参数而已，拿到这组超参数后我们就可以训练处我们的最佳模型 
  knn_clf = KNeighborsClassifier(weights='distance',n_neighbors=2,p=2)
# 用我们找到的k和p。来对X_train,y_train整体fit一下，来看他对X_test,y_test的测试结果
knn_clf.fit(X_train,y_train)
# 注意这个X_test,y_test在交叉验证过程中是完全没有用过的，也就是说我们这样得出的结果是可信的
knn_clf.score(X_test,y_test)
 
  0.98052851182197498
 
  回顾网格搜索 
  我们上面的操作，实际上在网格搜索的过程中已经进行了，只不过这个过程是sklean的网格搜索自带的一个过程 
  from sklearn.model_selection import GridSearchCV

param_grid = [
    {
        'weights': ['distance'],
        'n_neighbors': [i for i in range(2, 11)], 
        'p': [i for i in range(1, 6)]
    }
]

grid_search = GridSearchCV(knn_clf, param_grid, verbose=1)
grid_search.fit(X_train, y_train)
 
  Fitting 3 folds for each of 45 candidates, totalling 135 fits


[Parallel(n_jobs=1)]: Done 135 out of 135 | elapsed:  1.9min finished
 
  的意思就是交叉验证中分割了三组数据集，而我们的参数组合为9*6=45中组合
 3组数据集，45种组合，一共要进行135次的训练. 
      GridSearchCV(cv=None, error_score='raise',
           estimator=KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
               metric_params=None, n_jobs=1, n_neighbors=10, p=5,
               weights='distance'),
           fit_params={}, iid=True, n_jobs=1,
           param_grid=[{'weights': ['distance'], 'n_neighbors': [2, 3, 4, 5, 6, 7, 8, 9, 10], 'p': [1, 2, 3, 4, 5]}],
           pre_dispatch='2*n_jobs', refit=True, return_train_score=True,
           scoring=None, verbose=1)
 
  grid_search.best_score_
 
  0.98237476808905377
 
  grid_search.best_params_
 
  {'n_neighbors': 2, 'p': 2, 'weights': 'distance'}
 
  best_knn_clf = grid_search.best_estimator_
best_knn_clf.score(X_test, y_test)
 
  0.98052851182197498
 
  cv参数 
  cross_val_score(knn_clf, X_train, y_train, cv=5)
 
  array([ 0.99543379,  0.96803653,  0.98148148,  0.96261682,  0.97619048])
 
  # cv默认为3，可以修改改参数，修改修改不同分数的数据集
grid_search = GridSearchCV(knn_clf, param_grid, verbose=1, cv=5)
 
  总结 
   
  虽然整体速度慢了，但是这个结果却是可信赖的 
  模型正则化-Regularization 
  什么是模型正则化 
  下图是我们之前使用多项式回归过拟合一个样本的例子，可以看到这条模型曲线非常的弯曲，而且非常的陡峭，可以想象这条曲线的一些θ系数会非常的大。 模型正则化需要做的事情就是限制这些系数的大小 
   
  模型正则化基本原理 
   
  一些需要注意的细节： 
   
   对于θ的求和i是从1到n,没有将θ0加进去，因为他不是任意一项的系数，他只是一个截距，决定了整个曲线的高低，但是不决定曲线每一部分的陡峭和缓和。 
   θ求和的系数二分之一是一个惯例，加不加都可以，加上的原因是因为，将来对θ2>求导的时候可以抵消系数2，方便计算。不要也是可以的。 
   α实际上是一个超参数，代表在我们模型正则化下新的损失函数中，我们要让每一个θ尽可能的小，小的程度占我们整个损失函数的多少，如果α等于0，相当于没有正则化；如果α是正无穷的话，那么我们主要的优化任务就是让每一个θ尽可能的小。 
   
  岭回归 Ridge Regression 
   
  编程实现岭回归 
  岭回归 Ridge Regression 
  import numpy as np
import matplotlib.pyplot as plt
 
  np.random.seed(42)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x + 3 + np.random.normal(0, 1, size=100)
 
  plt.scatter(x, y)
plt.show()
 
   
  from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression

def PolynomialRegression(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lin_reg", LinearRegression())
    ])
 
  from sklearn.model_selection import train_test_split

np.random.seed(666)
X_train, X_test, y_train, y_test = train_test_split(X, y)
 
  from sklearn.metrics import mean_squared_error

poly_reg = PolynomialRegression(degree=20)
poly_reg.fit(X_train, y_train)

y_poly_predict = poly_reg.predict(X_test)
mean_squared_error(y_test, y_poly_predict)
 
  167.94010867293571
 
  X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = poly_reg.predict(X_plot)

plt.scatter(x, y)
plt.plot(X_plot[:,0], y_plot, color='r')
plt.axis([-3, 3, 0, 6])
plt.show()
 
   
  将绘制封装成函数 
  def plot_model(model):
    X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
    y_plot = model.predict(X_plot)

    plt.scatter(x, y)
    plt.plot(X_plot[:,0], y_plot, color='r')
    plt.axis([-3, 3, 0, 6])
    plt.show()

plot_model(poly_reg)
 
   
  使用岭回归 
  from sklearn.linear_model import Ridge

def RidgeRegression(degree, alpha):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("ridge_reg", Ridge(alpha=alpha))
    ])
 
  # 注意alpha后面的参数是所有theta的平方和，而对于多项式回归来说，岭回归之前得到的θ都非常大
# 我们前面系数alpha可以先取的小一些（正则化程度轻一些）
# 第一个参数是degree20, 0.0001是第二个参数alpha
ridge1_reg = RidgeRegression(20, 0.0001)
ridge1_reg.fit(X_train, y_train)

y1_predict = ridge1_reg.predict(X_test)
mean_squared_error(y_test, y1_predict)
 
  1.3233492754051845
 
  # 通过使用岭回归，使得我们的均方误差小了非常多,曲线也缓和了非常多
plot_model(ridge1_reg)
 
   
  ridge2_reg = RidgeRegression(20, 1)
ridge2_reg.fit(X_train, y_train)

y2_predict = ridge2_reg.predict(X_test)
mean_squared_error(y_test, y2_predict)
 
  1.1888759304218448
 
  # 让ridge2_reg 的alpha值等于1，均差误差更加的缩小，并且曲线越来越趋近于一根倾斜的直线
plot_model(ridge2_reg)
 
   
  ridge3_reg = RidgeRegression(20, 100)
ridge3_reg.fit(X_train, y_train)

y3_predict = ridge3_reg.predict(X_test)
mean_squared_error(y_test, y3_predict)
 
  1.3196456113086197
 
  # 得到的误差依然是比较小，但是比之前的1.18大了些，说明正则化做的有些过头了
plot_model(ridge3_reg)
 
   
  ridge4_reg = RidgeRegression(20, 10000000)
ridge4_reg.fit(X_train, y_train)

y4_predict = ridge4_reg.predict(X_test)
mean_squared_error(y_test, y4_predict)
 
  1.8408455590998372
 
  # 当alpha非常大，我们的模型实际上相当于就是在优化θ的平方和这一项，使得其最小（因为MSE的部分相对非常小）
# 而使得θ的平方和最小，就是使得每一个θ都趋近于0，这个时候曲线就趋近于一根直线了
plot_model(ridge4_reg)
 
   
  LASSO回归 
  使用|θ|代替θ2来标示θ的大小 
   
  Selection Operator – 选择运算符 
  LASSO回归有一些选择的功能 
   
  实际编程（准备代码参考上一节岭回归） 
  LASSO 
  import numpy as np
import matplotlib.pyplot as plt
 
  np.random.seed(42)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x + 3 + np.random.normal(0, 1, size=100)
 
  plt.scatter(x, y)
plt.show()
 
   
  from sklearn.model_selection import train_test_split

np.random.seed(666)
X_train, X_test, y_train, y_test = train_test_split(X, y)
 
  from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression

def PolynomialRegression(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lin_reg", LinearRegression())
    ])
 
  from sklearn.metrics import mean_squared_error

poly_reg = PolynomialRegression(degree=20)
poly_reg.fit(X_train, y_train)

y_predict = poly_reg.predict(X_test)
mean_squared_error(y_test, y_predict)
 
  167.94010867293571
 
  def plot_model(model):
    X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
    y_plot = model.predict(X_plot)

    plt.scatter(x, y)
    plt.plot(X_plot[:,0], y_plot, color='r')
    plt.axis([-3, 3, 0, 6])
    plt.show()

plot_model(poly_reg)
 
   
  from sklearn.linear_model import Lasso

def LassoRegression(degree, alpha):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lasso_reg", Lasso(alpha=alpha))
    ])
 
  lasso1_reg = LassoRegression(20, 0.01)
lasso1_reg.fit(X_train, y_train)

y1_predict = lasso1_reg.predict(X_test)
mean_squared_error(y_test, y1_predict)
 
  1.1496080843259966
 
  plot_model(lasso1_reg)
 
   
  lasso2_reg = LassoRegression(20, 0.1)
lasso2_reg.fit(X_train, y_train)

y2_predict = lasso2_reg.predict(X_test)
mean_squared_error(y_test, y2_predict)
 
  1.1213911351818648
 
  plot_model(lasso2_reg)
 
   
  lasso3_reg = LassoRegression(20, 1)
lasso3_reg.fit(X_train, y_train)

y3_predict = lasso3_reg.predict(X_test)
mean_squared_error(y_test, y3_predict)
 
  1.8408939659515595
 
  plot_model(lasso3_reg)
 
   
  总结Ridge和Lasso 
   
  α=100的时候，使用Ridge的得到的模型曲线依旧是一根曲线，事实上，使用Ridge很难得到一根倾斜的直线，他一直是弯曲的形状。 
  但是使用LASSO的时候，当α=0.1，虽然得到的依然是一根曲线，但是他显然比Radge的程度更低，更像一根直线。 
  这是因为LASSO趋向于使得一部分theta值为0（而不是很小的值），所以可以作为特征选择用，LASSO的最后两个字母SO就是Selection Operator的首字母缩写 使用LASSO的过程如果某一项θ等于0了，就说明LASSO Regression认为这个θ对应的特征是没有用的，剩下的那些不等于0的θ就说明LASSO Regression认为对应的这些特征有用，所以他可以当做特征选择用。 
   
   
  L1 范数常常用于特征选择 
  L2 范数常常用于防止模型过拟合 
  http://t.hengwei.me/post/%E6%B5%85%E8%B0%88l0l1l2%E8%8C%83%E6%95%B0%E5%8F%8A%E5%85%B6%E5%BA%94%E7%94%A8.html#1-l0-%E8%8C%83%E6%95%B0 
  https://zhuanlan.zhihu.com/p/29360425 
  集成学习(Ensemble Learning) 
  什么是集成学习 
  
 集成学习通过建立几个模型来解决单一预测问题。它的工作原理是生成多个分类器/模型，各自独立地学习和作出预测。这些预测最后结合成组合预测，因此优于任何一个单分类的做出预测。 
  机器学习的两个核心任务 
   
   任务一：如何优化训练数据 —> 主要用于解决欠拟合问题 
   任务二：如何提升泛化性能 —> 主要用于解决过拟合问题 
   
  大白话集成学习: 多种机器学习算法都能做同样的事情。让不同的算法针对同一个数据都跑一遍，最终使用投票的方法，少数服从多数，用多数投票的结果作为最终的结果。 
  import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
X, y = datasets.make_moons(n_samples=500, noise=0.3, random_state=42)
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
 
   
  from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
 
  自己实现集成学习 
   
   逻辑回归 
   
  from sklearn.linear_model import LogisticRegression
log_clf = LogisticRegression()
log_clf.fit(X_train, y_train)
log_clf.score(X_test, y_test)
 
  0.864 
  from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
 
   
   SVM 
   
  from sklearn.svm import SVC
svm_clf = SVC()
svm_clf.fit(X_train, y_train)
svm_clf.score(X_test, y_test)
 
  0.896 
   
   决策树 
   
  from sklearn.tree import DecisionTreeClassifier
dt_clf = DecisionTreeClassifier()
dt_clf.fit(X_train, y_train)
dt_clf.score(X_test, y_test)
 
  0.856 
  y_predict1 = log_clf.predict(X_test)
y_predict2 = svm_clf.predict(X_test)
y_predict3 = dt_clf.predict(X_test)
y_predict = y_predict1 + y_predict2 + y_predict3
y_predict
 
  array([2, 0, 1, 3, 3, 2, 0, 0, 0, 0, 3, 0, 3, 3, 3, 0, 0, 3, 2, 0, 0, 3,
 2, 0, 0, 0, 3, 0, 3, 0, 3, 3, 1, 0, 3, 1, 0, 3, 3, 3, 1, 3, 1, 1,
 0, 0, 2, 1, 3, 1, 2, 3, 0, 0, 1, 0, 2, 3, 0, 3, 0, 3, 3, 0, 3, 0,
 0, 1, 0, 3, 0, 0, 3, 2, 0, 0, 3, 3, 0, 0, 3, 2, 2, 1, 3, 2, 2, 0,
 3, 3, 3, 0, 0, 0, 0, 3, 0, 1, 1, 3, 0, 3, 3, 0, 0, 0, 0, 0, 2, 3,
 1, 0, 0, 2, 1, 0, 0, 0, 0, 3, 3, 3, 0, 0, 0]) 
  y_predict = np.array((y_predict1 + y_predict2 + y_predict3)>=2, dtype='int')
y_predict
 
  array([1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1,
 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0,
 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0,
 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0,
 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1,
 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0]) 
  from sklearn.metrics import accuracy_score
accuracy_score(y_test, y_predict)
 
  0.912 
   
   sklern中提供类似pipline的方式 
   
  使用VotingClassifier 
  from sklearn.ensemble import VotingClassifier
voteting_clf = VotingClassifier(estimators=[
    ('log_clf', LogisticRegression()),
    ('svm_clf', SVC()),
    ('dt_clf', DecisionTreeClassifier(random_state=666)),
], voting='hard')
voteting_clf.fit(X_train, y_train)
voteting_clf.score(X_test, y_test)
 
  0.904 
  Soft Voting Classifier 
  hard voting计算投票的方式是直接按照投票数量得出的
 soft voting 计算投票考虑了权重
 假如一个二分类问题，5个模型分别对一个样本进行分类。以下是每个模型认为每种分类的概率：
  
  按照hard voting，投票结果为A为2票,B为3票, 最终结果为A
 但考虑上每种类的概率
 
 投票结果为A
 
 
 
 逻辑回归，KNN，决策树（叶子结点的每个类的比例），都能估计概率。
 SVM本身没有考虑概率，因为它是计算margin。但SVM可以有一种方法来计算概率SVC(probability=True) 
   
   Hard 
   
  from sklearn.ensemble import VotingClassifier
voteting_clf = VotingClassifier(estimators=[
    ('log_clf', LogisticRegression()),
    ('svm_clf', SVC()),
    ('dt_clf', DecisionTreeClassifier(random_state=666)),
], voting='hard')
voteting_clf.fit(X_train, y_train)
voteting_clf.score(X_test, y_test)
 
  0.896 
   
   Soft 
   
  from sklearn.ensemble import VotingClassifier
voteting_clf2 = VotingClassifier(estimators=[
    ('log_clf', LogisticRegression()),
    ('svm_clf', SVC(probability = True)),
    ('dt_clf', DecisionTreeClassifier(random_state=666)),
], voting='soft')
voteting_clf2.fit(X_train, y_train)
voteting_clf2.score(X_test, y_test)
 
  0.912 
  Bagging 和 Pasting 
  虽然有很多机器学习的算法，但从投票的角度看，仍然不够多创建更多的子模型，集成更多子模型的意见
 子模型之间不能一致，子模型之间要有差异性, 如何创建差异性？
 解决方法：
 每个子模型只看样本数据的一部分。
 每个子模型不太需要太高的准确率。只要子模型足够多，准确率就会提高。
 例如500个子模型，每个子模型的准确率是60%，最终准确率能达到99.9% 
  Bagging集成原理 
  目标：把下面的圈和方块进行分类
 
 实现过程： 
   
   采样不同数据集
 
 2)训练分类器
 
 3)平权投票，获取最终结果
 
 4)主要实现过程小结 
   
   
  取样方法： 
   
   放回取样 bagging（bootstrap） 
   不放回取样 pasting 
   
  bagging更常用，优点： 
   
   没有那么依赖随机 
   数据量要求没那么高 
   
  使用 Bagging 
   
   
   决策树这种非参数的算法更容易产生差异较大的子模型 
   所有集成学习如果要集成成百上千个子模型，通常首先决策树 
   n_estimators：子模型数 
   max_samples：每个子模型看的样本树 
   bootstrap：放回取样 
   
  from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier
bagging_clf = BaggingClassifier(DecisionTreeClassifier(),
                                n_estimators=10, max_samples=100,
                                bootstrap=True)
bagging_clf.fit(X_train, y_train)
bagging_clf.score(X_test, y_test)
 
  0.888 
  bagging_clf = BaggingClassifier(DecisionTreeClassifier(),
                                n_estimators=10000, max_samples=100,
                                bootstrap=True)
bagging_clf.fit(X_train, y_train)
bagging_clf.score(X_test, y_test)
 
  0.912 
  随机森林 
   
   Bagging
 Base Estimator: Decision Tree
 只要是以决策树为基础的集成学习算法都叫随机森林。
 scikit-learn提供了随机森林算法，并为算法提供了更多的随机性。
 sickit-learn中，决策树在节点上划分，在随机的特征子集上寻找最优划分的特征。 
   
  随机森林构造过程 
  在机器学习中，随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定。
 随机森林 = Bagging + 决策树
 
 例如, 如果你训练了5个树, 其中有4个树的结果是True, 1个树的结果是False, 那么最终投票结果就是True 
  随机森林够造过程中的关键步骤(M表示特征数目)： 
   1)一次随机选出一个样本，有放回的抽样，重复N次(有可能出现重复的样本) 
   2) 随机去选出m个特征, m < 
  
随机森林api介绍 
  sklearn.ensemble.RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None, bootstrap=True, random_state=None, min_samples_split=2)
 
   
   n_estimators：integer，optional(default = 10)森林里的树木数量120,200,300,500,800,1200
 在利用最大投票数或平均值来预测之前，你想要建立子树的数量。 
   Criterion：string，可选(default =“gini”)分割特征的测量方法 
   max_depth：integer或None，可选(默认=无)树的最大深度 5,8,15,25,30 
   max_features="auto”,每个决策树的最大特征数量
 If “auto”, then max_features=sqrt(n_features).
 If “sqrt”, then max_features=sqrt(n_features)(same as “auto”).
 If “log2”, then max_features=log2(n_features).
 If None, then max_features=n_features. 
   bootstrap：boolean，optional(default = True)
 是否在构建树时使用放回抽样 
   min_samples_split 内部节点再划分所需最小样本数
 这个值限制了子树继续划分的条件，如果某节点的样本数少于min_samples_split，则不会继续再尝试选择最优特征来进行划分，默认是2。
 如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。 
   min_samples_leaf 叶子节点的最小样本数
 这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟节点一起被剪枝， 默认是1。
 叶是决策树的末端节点。 较小的叶子使模型更容易捕捉训练数据中的噪声。
 一般来说，我更偏向于将最小叶子节点数目设置为大于50。 
   min_impurity_split: 节点划分最小不纯度
 这个值限制了决策树的增长，如果某节点的不纯度(基于基尼系数，均方差)小于这个阈值，则该节点不再生成子节点。即为叶子节点 。
 一般不推荐改动默认值1e-7。 
   
  上面决策树参数中最重要的包括 
   
   最大特征数max_features 
   最大深度max_depth 
   内部节点再划分所需最小样本数min_samples_split 
   叶子节点最少样本数min_samples_leaf。 
   
  bagging集成优点 
   Bagging + 决策树/线性回归/逻辑回归/深度学习… = bagging集成学习方法
 经过上面方式组成的集成学习方法: 
   
   均可在原有算法上提高约2%左右的泛化正确率 
   简单, 方便, 通用 
   
  包外估计 (Out-of-Bag Estimate) 
  首先简单说一下什么是袋外样本oob (Out of bag)：在随机森林中，m个训练样本会通过bootstrap (有放回的随机抽样) 的抽样方式进行T次抽样每次抽样产生样本数为m的采样集，进入到并行的T个决策树中。这样有放回的抽样方式会导致有部分训练集中的样本(约36.8%)未进入决策树的采样集中，而这部分未被采集的的样本就是袋外数据oob, 而这个袋外数据就可以用来检测模型的泛化能力，和交叉验证类似。可以理解成从train datasets 中分出来的validation datasets。
 随机森林的 Bagging 过程，对于每一颗训练出的决策树 gt ，与数据集 D 有如下关系： 
  
 对于星号的部分，即是没有选择到的数据，称之为 Out-of-bag(OOB)数据，当数据足够多，对于任意一组数据 (xn,yn)(x_n, y_n)(xn,yn) 是包外数据的概率为： 
  
 由于基分类器是构建在训练样本的自助抽样集上的，只有约 63.2％ 原样本集出现在中，而剩余的 36.8％ 的数据作为包外数据，可以用于基分类器的验证集。 经验证，包外估计是对集成分类器泛化误差的无偏估计. 
   
   当基学习器是决策树时，可使用包外样本来辅助剪枝 ，或用于估计决策树中各结点的后验概率以辅助对零训练样本结点的处理；
 -当基学习器是神经网络时，可使用包外样本来辅助早期停止以减小过拟合 。 
   
  在随机森林算法中数据集属性的重要性、分类器集强度和分类器间相关性计算都依赖于袋外数据。 
  什么是oob_score 
  对于单棵用采样集训练完成的决策树Ti，用袋外数据运行后会产生一个oob_score (返回的是R square来判断)，对每一棵决策树都重复上述操作，最终会得到T个oob_score，把这T和oob_score平均，最终得到的就是整个随机森林的oob_score 
  import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
X, y = datasets.make_moons(n_samples=500, noise=0.3, random_state=666)
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
 
   
  from sklearn.ensemble import RandomForestClassifier
rf_clf = RandomForestClassifier(n_estimators=500, oob_score=True, random_state=666, n_jobs=-1)
rf_clf.fit(X, y)
rf_clf.oob_score_
 
  0.892 
  
# 随机森林拥有决策树和BaggingClassifier的所有参数：）

rf_clf2 = RandomForestClassifier(n_estimators=500,max_leaf_nodes=16, oob_score=True, random_state=666, n_jobs=-1)
rf_clf2.fit(X, y)
rf_clf2.oob_score_
 
  0.906 
  Kaggle实战 
  https://www.kaggle.com/c/otto-group-product-classification-challenge/overview
 奥托集团是世界上最大的电子商务公司之一，在20多个国家设有子公司。该公司每天都在世界各地销售数百万种产品,所以对其产品根据性能合理的分类非常重要。不过,在实际工作中,工作人员发现,许多相同的产品得到了不同的分类。本案例要求,你对奥拓集团的产品进行正确的分类。尽可能的提供分类的准确性。
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/8f195558c6ad4563bc19ab825a362c11.png 
  数据集介绍 
   
    本案例中，数据集包含大约200,000种产品的93个特征。
  
    其目的是建立一个能够区分otto公司主要产品类别的预测模型
  
    所有产品共被分成九个类别（例如时装，电子产品等）。
 
  
    id - 产品id
  
    feat_1, feat_2, …, feat_93 - 产品的各个特征
  
    target - 产品被划分的类别
  
   
  评分标准 
  本案例中，最后结果使用多分类对数损失进行评估。 
   
  Boosting 
  什么是boosting: 随着学习的积累从弱到强 
  简而言之：每新加入一个弱学习器，整体能力就会得到提升 
  代表算法：Adaboosting，GBDT，XGBoost，LightGBM
 
 实现过程：
 训练第一个学习器
 
 2.调整数据分布
 将错误的数据权重变的高一些, 正确的变得小一些
 
 3.训练第二个学习器
 
 4.再次调整数据分布
 
 5.依次训练学习器，调整数据分布
 
 6.整体过程实现
 
 前面的一类集成学习的思路(voting)：独立地集成多个模型，让各种子模型在视角上有差异化，并最终综合这些子模型的结果，获得学习的最终结果。
 另一类集成学习的思路叫做boosting。boosting即增强的意思。boosting也要集成多个模型，但每个模型都在尝试增强(boosting)整体的效果。子模型之间不是独立的关系。 
  
 原始数据集1 --某个算法1–> 某个模型1
 模型1没有很好学习的点的权值增大，很好学习到的点的权值减小，得到数据集2 --某个算法2 --> 某个模型2
 。。。
 每一个子模型都在推动上一个子模型犯的错误, 用这些子模型投票得到最终结果 
  bagging集成与boosting集成的区别： 
   
   区别一:数据方面 
   
   
   Bagging：对数据进行采样训练； 
   Boosting：根据前一轮学习结果调整数据的重要性。 
   
   
   区别二:投票方面 
   
   
   Bagging：所有学习器平权投票； 
   Boosting：对学习器进行加权投票。 
   
   
   区别三:学习顺序 
   
   
   Bagging的学习是并行的，每个学习器没有依赖关系； 
   Boosting学习是串行，学习有先后顺序。 
   
   
   区别四:主要作用 
   
   
   Bagging主要用于提高泛化性能（解决过拟合，也可以说降低方差） 
   Boosting主要用于提高训练精度 （解决欠拟合，也可以说降低偏差） 
   
  AdaBoosting 
  步骤一 ：初始化训练数据权重相等，训练第一个学习器。 
  该假设每个训练样本在基分类器的学习中作用相同，这一假设可以保证第一步能够在原始数据上学习基本分类器H1(x)H_1(x)H1(x)
 步骤二 ：AdaBoost反复学习基本分类器，在每一轮m=1,2,…,M顺次的执行下列操作：
 
 步骤三 ：对m个学习器进行加权投票
 
  
  案例 
  给定下面这张训练数据表所示的数据，假设弱分类器由xv产生，其阈值v使该分类器在训练数据集上的分类误差率最低，试用Adaboost算法学习一个强分类器。
 
 步骤一：初始化训练数据权重相等，训练第一个学习器：
 
 步骤二：AdaBoost反复学习基本分类器，在每一轮m=1,2,…,Mm=1,2,…,Mm=1,2,…,M顺次的执行下列操作： 
  当m=1的时候：
 
 当m=2的时候：
 
 当m=3的时候：
 
 步骤三：对m个学习器进行加权投票,获取最终分类器
  
  import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
X, y = datasets.make_moons(n_samples=500, noise=0.3, random_state=666)
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
 
   
  from sklearn.model_selection import train_test_split
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
ada_clf = AdaBoostClassifier(DecisionTreeClassifier(max_depth=2), n_estimators=500)
ada_clf.fit(X_train, y_train)
ada_clf.score(X_test, y_test)
 
  0.832 
  GBDT 
  GBDT 的全称是 Gradient Boosting Decision Tree，梯度提升树，在传统机器学习算法中，GBDT算的上TOP3的算法。 
  训练一个模型m1，产生错误e1
 针对e1训练第二个模型m2，产生错误e2
 针对e2训练第三个模型m3，产生错误e3
 。。。
 最终预测结果是m1+m2+m3+… 
   
  from sklearn.ensemble import GradientBoostingClassifier
GBDT = GradientBoostingClassifier(max_depth=2, n_estimators=30)
GBDT.fit(X_train, y_train)
GBDT.score(X_test, y_test)
 
  0.848
 想要理解GBDT的真正意义，那就必须理解GBDT中的Gradient Boosting 和Decision Tree分别是什么 
  Decision Tree：CART回归树 
  首先，GBDT使用的决策树是CART回归树，无论是处理回归问题还是二分类以及多分类，GBDT使用的决策树通通都是都是CART回归树。
 为什么不用CART分类树呢？ 因为GBDT每次迭代要拟合的是梯度值，是连续值所以要用回归树。
 对于回归树算法来说最重要的是寻找最佳的划分点，那么回归树中的可划分点包含了所有特征的所有可取的值。
 在分类树中最佳划分点的判别标准是熵或者基尼系数，都是用纯度来衡量的，但是在回归树中的样本标签是连续数值，所以再使用熵之类的指标不再合适，取而代之的是平方误差，它能很好的评判拟合程度。 
  回归树生成算法 
  输入：训练数据集D:
 输出：回归树 f(x)
 在训练数据集所在的输入空间中，递归的将每个区域划分为两个子区域并决定每个子区域上的输出值，构建二叉决策树：
  
  Gradient Boosting： 拟合负梯度 
  梯度提升树（Grandient Boosting）是提升树（Boosting Tree）的一种改进算法，所以在讲梯度提升树之前先来说一下提升树。 
  先来个通俗理解：假如有个人30岁，我们首先用20岁去拟合，发现损失有10岁，这时我们用6岁去拟合剩下的损失，发现差距还有4岁，第三轮我们用3岁拟合剩下的差距，差距就只有一岁了。如果我们的迭代轮数还没有完，可以继续迭代下面，每一轮迭代，拟合的岁数误差都会减小。最后将每次拟合的岁数加起来便是模型输出的结果。 
  提升树算法：
  
  上面伪代码中的残差是什么
  
  
 回到我们上面讲的那个通俗易懂的例子中，第一次迭代的残差是10岁，第二 次残差4岁, 
  当损失函数是平方损失和指数损失函数时，梯度提升树每一步优化是很简单的，但是对于一般损失函数而言，往往每一步优化起来不那么容易。针对这一问题，Friedman提出了梯度提升树算法，这是利用最速下降的近似方法，其关键是利用损失函数的负梯度作为提升树算法中的残差的近似值。
 那么负梯度长什么样呢？
 
 此时我们发现GBDT的负梯度就是残差，所以说对于回归问题，我们要拟合的就是残差。 
  那么对于分类问题呢？二分类和多分类的损失函数都是logloss。 
  GBDT算法原理