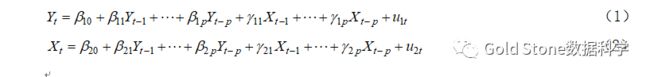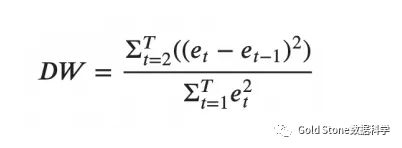adf检验代码 python_第22期：向量自回归（VAR）模型预测——Python实现

一、向量自回归模型简介

经典回归模型都存在一个强加单向关系的局限性，即被解释变量受到解释变量的影响，但反之不成立。然而，在许多情况下所有变量都相互影响。向量自回归(VAR)模型允许这类双向反馈关系，所有变量都被平等对待，即所有变量都是内生的，变量之间平等地相互影响。VAR模型将单变量自回归的思想扩展到多元时间序列回归，是单变量自回归模型的一般化。它由系统中每个变量对应一个方程组成。每个方程的等式右边都包含一个常数项和系统中所有变量的滞后项。两变量P阶VAR模型的一般表达式如下：                                                  

如果序列是平稳的，我们直接根据数据拟合 VAR 模型(称为“水平 VAR”)；如果序列非平稳，则将数据进行差分使其变得平稳，在此基础上拟合 VAR 模型(称为“差分 VAR”)。在这两种情况下，模型都是利用最小二乘法对方程逐一进行估计的。对于每个方程，通过最小化平方和的值来估计参数。

二、一个实例：使用VAR模型进行短期预测

(一)数据来源

本期应用案例为：Yash P. Mehra(1994)的文章《工资增长和通货膨胀过程：一种经验方法》所使用的时间序列数据集。

原文如下：

Mehra,Yash P. "Wage growth and the inflation process: an empiricalapproach." Cointegration. Palgrave Macmillan, London, 1994. 147-159.

CSV格式的数据集可以在下面网址下载。https://raw.githubusercontent.com/selva86/datasets/master/Raotbl6.csv

(二)变量

该数据集是8个变量的季度时间序列，变量如下：

1. rgnp :Real GNP.

2. pgnp :Potential real GNP.

3. ulc :Unit labor cost.

4. gdfco: Fixed weight deflator for personal consumption expenditure excluding food andenergy.

5. gdf :Fixed weight GNP deflator.

6. gdfim: Fixed weight import deflator.

7. gdfcf: Fixed weight deflator for food in personal consumption expenditure.

8. gdfce: Fixed weight deflator for energy in personal consumption expenditure.

三、计算过程与Python代码

#(1)载入包

importpandas as pd

importnumpy as np

importmatplotlib.pyplot as plt

%matplotlibinline

# ImportStatsmodels

fromstatsmodels.tsa.api import VAR

fromstatsmodels.tsa.stattools import adfuller

fromstatsmodels.tools.eval_measures import rmse, aic

#(2)导入数据

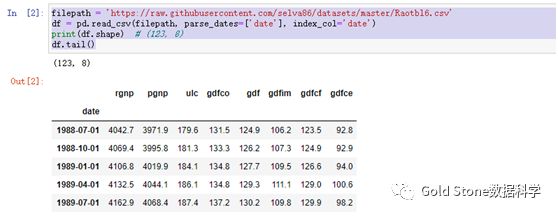
filepath= 'https://raw.githubusercontent.com/selva86/datasets/master/Raotbl6.csv'

df =pd.read_csv(filepath, parse_dates=['date'], index_col='date')

print(df.shape)  # (123, 8)

df.tail()

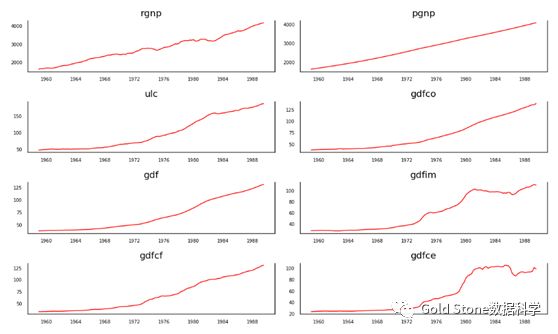
#(3)时间序列可视化

# Plot

fig,axes = plt.subplots(nrows=4, ncols=2, dpi=120, figsize=(10,6))

for i,ax in enumerate(axes.flatten()):

    data = df[df.columns[i]]

    ax.plot(data, color='red', linewidth=1)

    # Decorations

    ax.set_title(df.columns[i])

    ax.xaxis.set_ticks_position('none')

    ax.yaxis.set_ticks_position('none')

    ax.spines["top"].set_alpha(0)

    ax.tick_params(labelsize=6)

plt.tight_layout()

#(4)格兰杰因果检验

fromstatsmodels.tsa.stattools import grangercausalitytests

maxlag=12

test ='ssr_chi2test'

def grangers_causation_matrix(data,variables, test='ssr_chi2test', verbose=False):   

    """Check Granger Causalityof all possible combinations of the Time series.

    The rows are the response variable, columnsare predictors. The values in the table

    are the P-Values. P-Values lesser than thesignificance level (0.05), implies

    the Null Hypothesis that the coefficientsof the corresponding past values is

    zero, that is, the X does not cause Y canbe rejected.

    data     : pandas dataframe containing the time series variables

    variables : list containing names of thetime series variables.

    """

    df = pd.DataFrame(np.zeros((len(variables),len(variables))), columns=variables, index=variables)

    for c in df.columns:

        for r in df.index:

            test_result =grangercausalitytests(data[[r, c]], maxlag=maxlag, verbose=False)

            p_values =[round(test_result[i+1][0][test][1],4) for i in range(maxlag)]

            if verbose: print(f'Y = {r}, X ={c}, P Values = {p_values}')

            min_p_value = np.min(p_values)

            df.loc[r, c] = min_p_value

    df.columns = [var + '_x' for var invariables]

    df.index = [var + '_y' for var invariables]

    return df

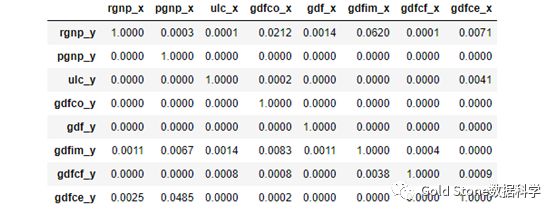
grangers_causation_matrix(df,variables = df.columns)  

上述结果中，行是响应变量(Y)，列是预测变量(X)。

例如，(行1，列2)的P值0.0003<显着性水平(0.05)，pgnp_x是导致rgnp_y的格兰杰原因。其它相同的解释。

接下来进行变量间的协整检验。

#(5)协整检验

fromstatsmodels.tsa.vector_ar.vecm import coint_johansen

defcointegration_test(df, alpha=0.05):

    """Perform Johanson'sCointegration Test and Report Summary"""

    out = coint_johansen(df,-1,5)

    d = {'0.90':0, '0.95':1, '0.99':2}

    traces = out.lr1

    cvts = out.cvt[:, d[str(1-alpha)]]

    def adjust(val, length= 6): returnstr(val).ljust(length)

    # Summary

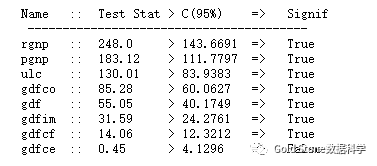
    print('Name   :: Test Stat > C(95%)   =>   Signif  \n', '--'*20)

    for col, trace, cvt in zip(df.columns,traces, cvts):

        print(adjust(col), ':: ',adjust(round(trace,2), 9), ">", adjust(cvt, 8), ' =>  ' , trace > cvt)

cointegration_test(df)

结果如下：

接下来，将数据集分为训练和测试数据。

VAR模型将被拟合df_train，然后用于预测接下来的4个观测值。这些预测将与测试数据中的实际值进行比较。

为了进行比较，我们将使用多个预测准确性指标。

#(6)数据集分为训练和测试数据

nobs = 4

df_train,df_test = df[0:-nobs], df[-nobs:]

# Checksize

print(df_train.shape)  # (119, 8)

print(df_test.shape)  # (4, 8)

#(7)序列平稳性检验

三种最常用的检验方法：ADF、KPSS和PP检验法。

defadfuller_test(series, signif=0.05, name='', verbose=False):

    """Perform ADFuller to testfor Stationarity of given series and print report"""

    r = adfuller(series, autolag='AIC')

    output = {'test_statistic':round(r[0], 4),'pvalue':round(r[1], 4), 'n_lags':round(r[2], 4), 'n_obs':r[3]}

    p_value = output['pvalue']

    def adjust(val, length= 6): returnstr(val).ljust(length)

    # Print Summary

    print(f'   Augmented Dickey-Fuller Test on "{name}"', "\n   ", '-'*47)

    print(f' Null Hypothesis: Data has unitroot. Non-Stationary.')

    print(f' Significance Level    = {signif}')

    print(f' Test Statistic        ={output["test_statistic"]}')

    print(f' No. Lags Chosen       = {output["n_lags"]}')

    for key,val in r[4].items():

        print(f' Critical value {adjust(key)} ={round(val, 3)}')

    if p_value <= signif:

        print(f" => P-Value ={p_value}. Rejecting Null Hypothesis.")

        print(f" => Series isStationary.")

    else:

        print(f" => P-Value ={p_value}. Weak evidence to reject the Null Hypothesis.")

        print(f" => Series isNon-Stationary.")

# ADFTest on each column

forname, column in df_train.iteritems():

    adfuller_test(column, name=column.name)

print('\n')

结果如下：

上述结果发现，ADF检验确认没有时间序列是平稳的。因此各序列一次差分后再检验。差分后的序列都平稳(只列出了两个差分序列的检验结果)。

# 1st difference

df_differenced = df_train.diff().dropna()

# ADF Test on each column of 1st Differences Dataframe

for name, column in df_differenced.iteritems():

    adfuller_test(column,name=column.name)

    print('\n')

#(8)选择VAR模型的阶数(P)

四个最常用的信息准则：AIC、BIC、FPE和HQIC。

model = VAR(df_differenced)

for i in [1,2,3,4,5,6,7,8,9]:

    result = model.fit(i)

    print('Lag Order =', i)

    print('AIC : ',result.aic)

    print('BIC : ',result.bic)

    print('FPE : ',result.fpe)

    print('HQIC: ',result.hqic, '\n')

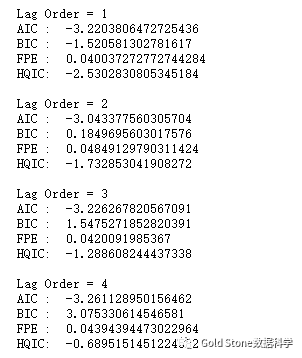
结果如下：

在上面的输出中，AIC在滞后4处降至最低，然后在滞后5处增加，然后连续进一步下降，所以使用滞后4模型。

选择VAR模型的阶数(p)的另一种方法是使用该方法：model.select_order(maxlags)

所选顺序(p)是给出最低“ AIC”，“ BIC”，“ FPE”和“ HQIC”值的顺序。

x =model.select_order(maxlags=12)

x.summary()

结果如下：

根据FPE和HQIC，最佳滞后阶数为3。

#(9)训练VAR模型

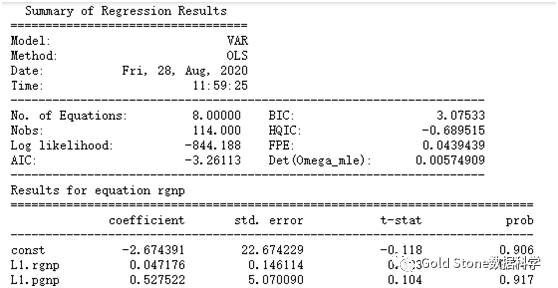
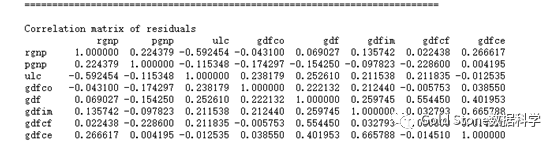
model_fitted= model.fit(4)

model_fitted.summary()

…………(省略)

#(10)Durbin Watson统计量检查残差(误差)的序列相关性

使用Durbin Watson统计量检查残差项的序列相关性的公式如下:

DW值可以在0到4之间变化。它越接近值2，则没有明显的序列相关性。接近0时，存在正序列相关，而接近4时，则具有负序列相关。

from statsmodels.stats.stattools import durbin_watson

out = durbin_watson(model_fitted.resid)

for col, val in zip(df.columns, out):

    print(adjust(col), ':',round(val, 2))

结果如下:

rgnp : 2.09

pgnp : 2.02

ulc : 2.17

gdfco : 2.05

gdf : 2.25

gdfim : 1.99

gdfcf : 2.2

gdfce : 2.17

#(11)VAR模型预测

# Get the lag order

lag_order = model_fitted.k_ar

print(lag_order)  #> 4

# Input data for forecasting

forecast_input = df_differenced.values[-lag_order:]

forecast_input

#预测

# Forecast

fc = model_fitted.forecast(y=forecast_input, steps=nobs)

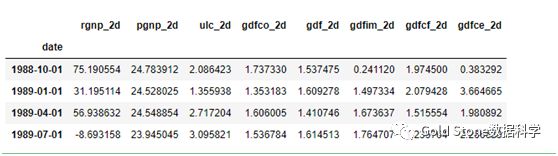
df_forecast = pd.DataFrame(fc, index=df.index[-nobs:],columns=df.columns + '_2d')

df_forecast

生成了预测，但是预测值是模型使用的训练数据得到的结果。因此，要将其恢复到原始比例，需要对原始输入数据进行多次差异化处理。

在这种情况下，它是两次。

#(12)变换以获得真实的预测值

def invert_transformation(df_train, df_forecast, second_diff=False):

    """Revertback the differencing to get the forecast to original scale."""

    df_fc = df_forecast.copy()

    columns = df_train.columns

    for col in columns:       

        # Roll back 2nd Diff

        if second_diff:

            df_fc[str(col)+'_1d']= (df_train[col].iloc[-1]-df_train[col].iloc[-2]) +df_fc[str(col)+'_2d'].cumsum()

        # Roll back 1st Diff

       df_fc[str(col)+'_forecast'] = df_train[col].iloc[-1] +df_fc[str(col)+'_1d'].cumsum()

    return df_fc

f_results = invert_transformation(train, df_forecast,second_diff=True)       

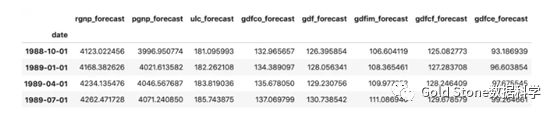
df_results.loc[:, ['rgnp_forecast', 'pgnp_forecast', 'ulc_forecast','gdfco_forecast',

                  'gdf_forecast', 'gdfim_forecast', 'gdfcf_forecast', 'gdfce_forecast']]

结果：

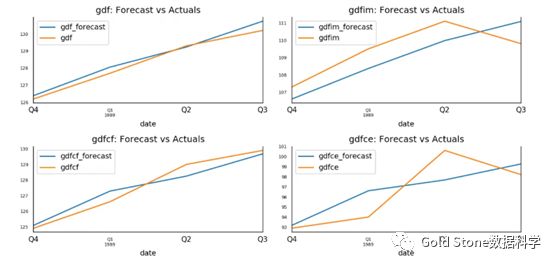
#(12)预测值与实际值可视化

fig, axes = plt.subplots(nrows=int(len(df.columns)/2), ncols=2,dpi=150, figsize=(10,10))

for i, (col,ax) in enumerate(zip(df.columns, axes.flatten())):

   df_results[col+'_forecast'].plot(legend=True,ax=ax).autoscale(axis='x',tight=True)

   df_test[col][-nobs:].plot(legend=True, ax=ax);

    ax.set_title(col + ":Forecast vs Actuals")

   ax.xaxis.set_ticks_position('none')

   ax.yaxis.set_ticks_position('none')

   ax.spines["top"].set_alpha(0)

   ax.tick_params(labelsize=6)

plt.tight_layout();

最后，本期特感谢：

Selva Prabhakaran博士对VAR模型Python代码的提供，可参阅网站：

https://www.machinelearningplus.com/time-series/vector-autoregression-examples-python/