机器学习性能评价指标的适用情境

评估机器学习算法的性能是所有项目的重要组成部分。 当使用诸如 accuracy_score 等指标进行评估时，您的模型可能会给您带来令人满意的结果，但当使用其他指标（例如 logarithmic_loss 等）进行评估时，结果可能会很差。在实际应用中，我们会根据不同的任务需求选择不同的评价指标，在对比不同模型的能力时，使用不同的评价指标往往会导致不同的评价结果。这一结果表明，模型的“好坏”是相对的。什么样的模型是好模型？这一问题不仅取决于算法和数据，还与任务需求密切相关。

建模不是目的。先建模，然后选择一个能准确预测样本的模型，才是根本目的。

评价指标的选择完全取决于模型的类型（分类或回归）和目标（任务需求）。在这篇文章中，我们将介绍不同类型评价指标的适合情境和缺点：

1. 模型的类型
当我们谈论预测模型时，我们谈论的是回归模型（连续输出）或分类模型（标称类型或二元类型输出）。每个模型中使用的评估指标都不同。
1.1 在分类问题中，我们使用两种类型（根据输出类型分类）的算法：
（1）类输出：SVM 和 KNN 等算法创建类输出。例如，在二进制分类问题中，输出将是 0 或 1。但是，我们现在有一些算法可以将这些类输出转换为概率。但是这些算法并没有被统计界很好地接受。
（2）概率输出：逻辑回归、随机森林、梯度提升、Adaboost 等算法给出概率输出。将概率输出转换为类输出，只需要我们创建一个概率阈值。
1.2 在回归问题中，我们没有这样的输出不一致。输出本质上始终是连续的，无需进一步处理。
参考7总结了scikit-learn中的所有评价指标可以作为参考。

在介绍这些指标前，我们需要先了解几个概念：

1. ndarray
   numpy中的ndarray为多维数组，是numpy中最为重要也是python进行科学计算非常重要和基本的数据类型。ndarray中的重要属性有：
   （1）shape
   shape属性是一个表示数组形状（各维度大小）的元组。比如一个二维的4*5数组shape为(4,5)，4行5列。

2. 分类模型的评价指标
2.1 Confusion Matrix（混淆矩阵）
（1）理论及适用条件
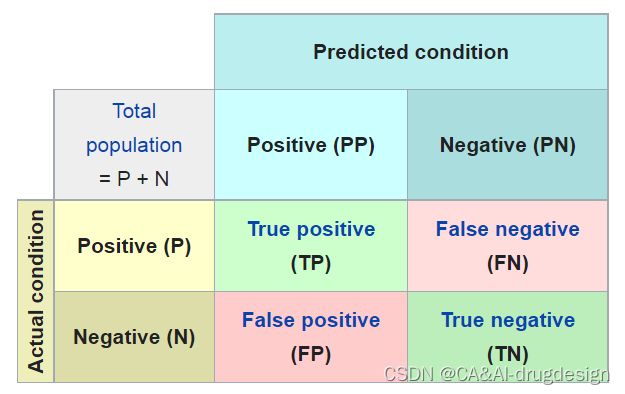
在机器学习领域，特别是统计分类问题中，混淆矩阵，也称为误差矩阵，是一种特定的表格布局。该布局使得算法的性能可视化，通常适用于监督学习算法（在无监督学习中，它通常被称为匹配矩阵）。 矩阵的每一行代表实际类中的实例，而每一列代表预测类中的实例，反之亦然——这两种变体都可以在文献中找到。这个名字源于这样一个事实：它使人们很容易看到系统是否混淆了两个类（即通常将一个类错误地标记为另一个类）。

它是一种特殊的列联表（观测数据按两个或更多属性（定性变量）分类时所列出的频数表），有两个维度（“实际”和“预测”），并且在两个维度上都有相同的“类”集（维度和类的每个组合都是列联表中的一个变量）。

“实际类”
P（阳性）： condition positive—数据中正类样本的数量
N（阴性）： condition negative—数据中负类样本的数量
“预测类”
TP（真阳性）： true positive—将正类样本预测为正
TN（真阴性）：true negative—将负类样本预测为负
FP（假阳性）：false positive—将负类样本预测为正
FN（假阴性）：false negative—将正类样本预测为负

对于一个二分类任务，二分类器的预测结果可分为4类（TP、TN、FP和FN），这四种结果可以用一个2×2的混淆矩阵来表述：

可以看出，系统分类正确的TP和TN在混淆矩阵的主对角线上，而分类错误的样本在副对角线上。所以我们希望混淆矩阵主对角线上的值更大，而副对角线上的值更小。

如果是多分类问题，比如10类，那么混淆矩阵将会是十行十列的矩阵，但是与二分类相同的是，主对角线上的部分是系统分类正确的部分，所以依旧希望主对角线上的值更大，而主对角线以外的部分都是分类错误的部分。

（2）如何用sklearn包计算confusion matrix

①我们可以使用sklearn包下面的metrics模块里面的函数“confusion_matrix”来计算每两个类之间的一个混淆矩阵 ：
sklearn.metrics.confusion_matrix(y_true, y_pred, *, labels=None, sample_weight=None, normalize=None)

参数：

参数名	含义	形式
y_true	正确标签	一维数组，或标签指示数组/稀疏矩阵（0比1多即为稀疏）
y_pred	分类器预测的标签	一维数组，或标签指示数组/稀疏矩阵
normalize	用真实数据（行）、预测数据（列）或所有数据标准化混淆矩阵。如果设置为None，混淆矩阵将不会被标准化	{‘true’, ‘pred’, ‘all’}, default=None
sample_weight	样品权重	array-like of shape (n_samples,), default=None
labels	用于对矩阵进行索引的标签列表，这个可能可以用于对标签进行重排序或者选择一小部分标签。如果设置为None，在y_true或y_pred中出现至少一次的标签将按顺序排列	array-like of shape (n_classes), default=None

返回：
C：ndarray of shape (n_classes, n_classes)
混淆矩阵，其第 i 行第 j 列条目表示真实标签为第 i 类且预测标签为第 j 类的样本数。

from sklearn.metrics import confusion_matrix
y_true = [2, 0, 2, 2, 0, 1]
y_pred = [0, 0, 2, 2, 0, 2]
confusion_matrix(y_true, y_pred)
# array([[2, 0, 0],
       [0, 0, 1],
       [1, 0, 2]])

y_true = ["cat", "ant", "cat", "cat", "ant", "bird"]
y_pred = ["ant", "ant", "cat", "cat", "ant", "cat"]
confusion_matrix(y_true, y_pred, labels=["ant", "bird", "cat"])
# array([[2, 0, 0],
       [0, 0, 1],
       [1, 0, 2]])

#In the binary case, we can extract true positives, etc as follows:
tn, fp, fn, tp = confusion_matrix([0, 1, 0, 1], [1, 1, 1, 0]).ravel()
print(tn, fp, fn, tp)
# (0, 2, 1, 1)

②我们可以使用sklearn包下面的metrics模块里面的函数“multilabel_confusion_matrix”计算class-wise或sample-wise的多标签混淆矩阵，在多分类任务中，标签以one-vs-rest way的方式被二进制化：
sklearn.metrics.multilabel_confusion_matrix(y_true, y_pred, *, sample_weight=None, labels=None, samplewise=False)

参数：

参数名	含义	形式
y_true	正确标签	一维数组，或标签指示数组/稀疏矩阵（0比1多即为稀疏）
y_pred	分类器预测的标签	一维数组，或标签指示数组/稀疏矩阵
labels	选择一些类的列表（或者可以强制纳入一些数据中心没有的类）	array-like of shape (n_classes,), default=True
sample_weight	样品权重	array-like of shape (n_samples,), default=None
samplewise	在多标签（多分类）情况下，这个参数计算每个样品的混淆矩阵	布尔, default=None

返回：
多重混淆：ndarray of shape (n_outputs, 2, 2)
一个2x2的混淆矩阵对应于输入中的每个输出。当计算class-wise的多重混淆（默认）时，n_outputs = n_labels。当计算sample-wise的多重混淆（samplewise=True）时，n_outputs = n_samples。如果定义了labels，返回的结果为指定顺序的labels。否则，结果将按默认的排序顺序返回。

#Multilabel-indicator case:
import numpy as np
from sklearn.metrics import multilabel_confusion_matrix
y_true = np.array([[1, 0, 1],
...                         [0, 1, 0]])
y_pred = np.array([[1, 0, 0],
...                            [0, 1, 1]])
multilabel_confusion_matrix(y_true, y_pred)
array([[[1, 0],
        [0, 1]],

       [[1, 0],
        [0, 1]],

       [[0, 1],
        [1, 0]]])

以下其他分类模型的评价指标均为基于混淆矩阵的拓展指标。

2.2 Accuracy（ACC）
（1）理论及适用条件
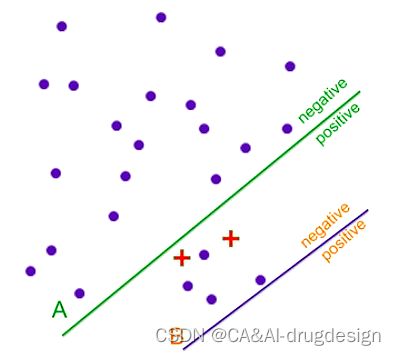
检测时分对的样本数除以所有的样本数。准确率一般被用来评估检测模型的全局准确程度，是评价分类系统好坏的基本指标，又称精度。但是，对于分布不均衡的样本，即对于样本中正例（Positive）数量远远少于反例（Negative）的情况，这个指标将不再可靠。
$$ACC=\frac{TP+TN}{TP+TN+FP+FN}$$
例如：
假设我们要预测某篇文章的作者是否会得诺贝尔奖，我们收集了一些文章，只有极少的文章作者是诺贝尔奖得主，用红色加号表示。有两个系统A和B,系统A正确的分出了两个诺贝尔得主的文章，但是也错分了几个，系统B是只会预测否（Negative），无论什么文章都预测其作者不是诺贝尔奖得主。如果让人去选择，应该会更倾向于系统A，至少会给出一些正例的信息，但如果用准确率作为评价指标，将会更倾向于选择错误率更少的系统B，系统A分错了四个样本，而系统B只分错了两个。可见，准确率更高的系统不一定是更好的系统。

（2）如何用sklearn包计算ACC
我们可以使用sklearn包下面的metrics模块里面的函数“accuracy_score”：
sklearn.metrics.accuracy_score(y_true, y_pred, *, normalize=True, sample_weight=None)

参数：

参数名	含义	形式
y_true	正确标签	一维数组，或标签指示数组/稀疏矩阵（0比1多即为稀疏）
y_pred	分类器预测的标签	一维数组，或标签指示数组/稀疏矩阵
normalizebool	如果是False，返回正确分类的样本数。否则，返回正确分类的样本的分数。	default=True
sample_weight	样品权重	array-like of shape (n_samples,), default=None

举例说明：

from sklearn.metrics import accuracy_score
y_pred = [0, 2, 1, 3]  #真实标签
y_true = [0, 1, 2, 3]  #预测标签
sample_weight=[0.1, 0.2, 0.6, 0.1]
accuracy_score(y_true, y_pred)  #正确分类的样本分数，为50%
0.5
accuracy_score(y_true, y_pred, normalize=False)   #正确分类的样本个数，为2
2
accuracy_score(y_true, y_pred, sample_weight=sample_weight) #设置权重
0.2
# 在具有二进制标签指示符的多标签情况下
import numpy as np
a=np.array([[0, 1], [1, 1]])
print(a)  # [[0 1], [1 1]]
b=np.ones((2, 2))
print(b) # [[1. 1.], [1. 1.]]
c=accuracy_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2)))
print(c) #0.5

2.3 precision
（1）理论及适用条件
定义：又称查准率或“准确率”或“精度”，正确分类的正例个数占分类为正例的实例个数的比例。用于直观地表示分类器标记正例（positive）的能力。
$$precision=\frac{TP}{TP+FP}$$

适用条件：以西瓜问题为例，假定瓜农拉来一车西瓜，我们用训练好的模型对这些西瓜进行判别。accuray衡量了有多少比例的西瓜被判别正确。但是，假如我们关心的是“挑出的西瓜中有多少比例是好瓜”（precision，查准率），或者**“所有好瓜中有多少比例被挑出来”（recall，查全率）**，这时就需要使用其他的性能度量了。

（2）如何用sklearn包计算precision
我们可以使用sklearn包下面的metrics模块里面的函数“precision_score”：
sklearn.metrics.precision_score(y_true, y_pred, *, labels=None, pos_label=1, average=‘binary’, sample_weight=None, zero_division=‘warn’)

参数：

参数名	含义	形式
y_true	正确标签	一维数组，或标签指示数组/稀疏矩阵（0比1多即为稀疏）
y_pred	分类器预测的标签	一维数组，或标签指示数组/稀疏矩阵
average	对于多分类/多标签的情况下，此参数是必需的。**如果为None，则返回每个类的分数。**否则，将按照指定“average”的方法来对数据集进行处理。------binary：仅报告由pos_label指定的类的结果，（y_ {true,pred}）为二进制时才适用----‘micro’:通过计算总的TP、FN和FP来整体计算指标---- ‘macro’：计算每个标签的未加权均值（不考虑不平衡）。----‘samples’:计算每个实例找出其均值（仅对多标签分类有意义，这与 accuracy_score 不同）。—‘weighted’:计算每个标签的加权均值（每个标签的真实实例数），与macro相比，考虑了不平衡，它可能导致 F 分数不在精确率和召回率之间。	{‘micro’, ‘macro’, ‘samples’, ‘weighted’, ‘binary’} or None, default=’binary’
labels	当average！='binary’时所包含的一组标签，如果average是None，则为标签的顺序。数据中存在的标签可以被排除，例如，可以忽略多数negative类来计算多类average。当标签不存在数据中时，将导致average=“macro” 时出现0组成。对于多标签目标，标签是列索引。 默认情况下，y_true和y_pred中的所有标签均按排序的顺序使用。	类似数组的，default=None
pos_label	如果average='binary’并且数据是binary，报告分类。如果数据是多分类或者多标签的，则将被忽略。设置labels=[pos_label]和 average != ‘binary’，将仅仅报告标签的分数。	str or int, default=1
zero_division	当有除0错误的时候设置返回的值。如果设置为“ warn”，则该值为0，但也会发出警告。	“warn”, 0 or 1, default=”warn”

返回值：
精密度：浮点值（如果average非空）或形状的浮点值数组(n_unique_labels,)

关于参数Labels的理解：

第一个预测的，第二个是真实的。一共有四个类"blue", “white”, “yellow”, “red”，但是我不想关注"yellow"这一类，那么我在调用precision_score时，设置参数labels=[“blue”, “white”, “red”]。这个参数用于多分类的。

关于参数average的理解：

from sklearn.metrics import precision_score
y_true = [0, 1, 2, 0, 1, 2]
y_pred = [0, 2, 1, 0, 0, 1]
precision_score(y_true, y_pred, average='macro')
0.22
precision_score(y_true, y_pred, average='micro')
0.33...
precision_score(y_true, y_pred, average='weighted')
0.22...
precision_score(y_true, y_pred, average=None)
array([0.66..., 0.        , 0. ])
y_pred = [0, 0, 0, 0, 0, 0]
precision_score(y_true, y_pred, average=None)
array([0.33..., 0.        , 0.  ])
precision_score(y_true, y_pred, average=None, zero_division=1)
array([0.33..., 1. , 1.  ])
# multilabel classification
y_true = [[0, 0, 0], [1, 1, 1], [0, 1, 1]]
y_pred = [[0, 0, 0], [1, 1, 1], [1, 1, 0]]
precision_score(y_true, y_pred, average=None)
array([0.5, 1. , 1. ])

2.4 Recall
（1）理论及适用条件
定义：正确分类的正例个数占实际正例个数的比例，也称查全率或召回率。用于直观地表示分类器找到所有正样本的能力。
$$recall=\frac{TP}{TP+FN}$$
适用条件：如果我们关心“所有好瓜中有多少比例被挑出来”，就可以使用recall。precision通常与recall一起使用。precision与recall是一对矛盾的度量，一般来说，precision高时，recall低；recall高时，precision低。例如，如果我们希望将好瓜尽可能多地选出来，则可以通过增加选瓜的数量来实现。如果将所有西瓜都选上，那么所有的好瓜也必然都被选上了，这样recall为100%（FN=0）。若希望选出的瓜好瓜的比例尽可能高，则可以只选择最有把握的瓜（如果只选择一个，则FP=0，precision=1），但这样难免会漏掉不少好瓜（FN增加），使得recall较低。

通常只有在一些简单任务中，才可能使查全率和查准率都很高，也就是FP（假阳）和FN（假阴）都比较低。

比如在搜索网页时，如果只返回最相关的一个网页，那precision就是100%，而recall就很低（其他相关网页FN的多了）；如果返回全部网页，那recall为100%（FN=0），precision就很低。因此在不同场合需要根据实际需求判断哪个指标更重要。

（2）如何用sklearn包计算recall
我们可以使用sklearn包下面的metrics模块里面的函数“recall_score”：
sklearn.metrics.recall_score(y_true, y_pred, *, labels=None, pos_label=1, average=‘binary’, sample_weight=None, zero_division=‘warn’)

参数：
与precision相同

返回值：
精密度：浮点值（如果average非空）或形状的浮点值数组(n_unique_labels,)
对二分类中正类的召回或多分类任务中每个类召回的加权平均。

from sklearn.metrics import recall_score
y_true = [0, 1, 2, 0, 1, 2]
y_pred = [0, 2, 1, 0, 0, 1]
recall_score(y_true, y_pred, average='macro')
0.33...
recall_score(y_true, y_pred, average='micro')
0.33...
recall_score(y_true, y_pred, average='weighted')
0.33...
recall_score(y_true, y_pred, average=None)
array([1., 0., 0.])
y_true = [0, 0, 0, 0, 0, 0]
recall_score(y_true, y_pred, average=None)
array([0.5, 0. , 0. ])
recall_score(y_true, y_pred, average=None, zero_division=1)
array([0.5, 1. , 1. ])

# multilabel classification
y_true = [[0, 0, 0], [1, 1, 1], [0, 1, 1]]
y_pred = [[0, 0, 0], [1, 1, 1], [1, 1, 0]]
recall_score(y_true, y_pred, average=None)
array([1. , 1. , 0.5])

2.5 PR Curve
（1）理论及适用条件
改变模型中用于做出分类决策的阈值，是一种调节给定分类器的precision和recall之间折中的方法。你可能希望仅遗漏不到10%的正类样本，即希望recall能达到90%。这一决策取决于应用，应该是由商业目标驱动的。一旦设定了一个具体目标（比如对某一类别的特定recall或precision），就可以适当地设定一个阈值。总是可以设置一个阈值来满足特定的目标，比如90%的recall。难点在于开发一个模型，在满足这个阈值的同时仍具有合理的准确率——如果你将所有样本都划为正类，那么将会得到100%的recall，但你的模型毫无用处。

**对分类器设置要求（比如90%的recall）通常被称为设置工作点。**在业务中固定工作点通常有助于为客户或组织内的其他小组提供性能保证。

在开发新模型时，通常并不完全清楚工作点在哪里。因此，为了更好地理解建模问题，很有启发性的做法是，同时查看所有可能的阈值或准确率和召回率的所有可能折中。利用一种叫准确率-召回率曲线（precision-recall curve）的工具可以做到这一点。

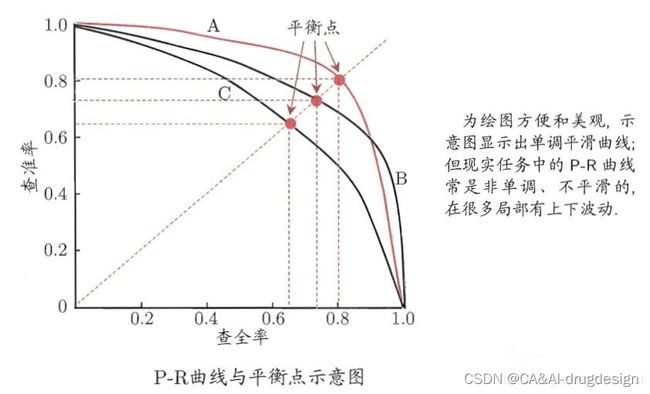
在很多情形下，我们可根据学习器的预测结果对样例进行排序，排在前面的是学习器认为“最可能”是正例的样本，排在最后的则是学习器认为“最不可能”是正例的样本。按此顺序逐个把样本作为正例进行预测，即以当前点概率为划分阈值，前面判为正例，后面判为反例，计算当前的precision和recall。以precision（查准率）为纵轴，以recall（查全率）为横轴，绘制曲线。

举例：
若数据库有500条记录，其中50个相关(正样本)，假设通过一个学习器后预测概率排序，以当前概率为阈值，返回了75个1，其中45个是真正的1。

则recall= 45/50 = 0.9； P = 45/75 = 0.6；则当前点的坐标即为（0.9，0.6）。依次类推。。。

如果一个学习器的P-R曲线被另一个学习器的P-R曲线完全包住，则可断言后者的性能优于前者（同一测试集上），例如上面的A和B优于学习器C，但是A和B的性能无法直接判断，但我们往往仍希望把学习器A和学习器B进行一个比较，我们可以根据曲线下方的面积大小来进行比较，但更常用的是平衡点或者是F1值。

曲线下的面积叫AP分数，能在一定程度上反应模型的精确率和召回率都很高的比例。但这个值不方便计算

平衡点（Break-Even Point，BEP）是precision=recall时的取值，如果这个值较大，则说明学习器的性能较好。但BEP还是过于简化了些，更常用的是F1度量。F1 = 2×P×R／(P+R)，同样，F1值越大，我们可以认为该学习器的性能较好。

（2）如何用sklearn包计算PR Curve
我们可以使用sklearn包下面的metrics模块里面的函数“precision_recall_curve”：
sklearn.metrics.precision_recall_curve(y_true, probas_pred, *, pos_label=None, sample_weight=None)

参数：

参数名	含义	形式
y_true	正确标签	n维数组（形状=n_samples），真正的二进制标签。如果标签不是{-1，1}或{0，1}，那么应该明确给出pos_label
probas_pred	目标得分（target score），可以是正类的概率估计，也可以是决策的非阈值测量（如某些分类器上的 decision_function 所返回的）。	n维数组（形状=n_samples）
pos_label	正类的标签。当pos_label=None时，如果y_true在{-1，1}或{0，1}中，pos_label被设置为1，否则将产生错误。	int or str, default=None
sample_weight	样品权重	类数组(shape=n_samples,), default=None

类数组的定义：
书面有这么一句定义来阐述类数组对象：只包含使用从零开始，且自然递增的整数做键名，并且定义了length表示元素个数的对象，我们就认为它是类数组对象。

举个例子：

var array = [‘zhangsan’, ‘lisi’, ‘zhaoliu’];

var arrayLike = {
0: ‘zhangsan’,
1: ‘lisi’,
2: ‘zhaoliu’,
length: 3
}

代码块中的arrayLike对象就是一个类数组对象（包含了0、1、2三个索引和一个length属性）。

数组和类数组从数据获取和值设置的角度，无论是获取数据还是对对象属性值进行设定，以及长度length值获取和自身的遍历运用，用法是非常相似的。

需要注意的是，在遇到遍历的需求的时候，实际上数组的效率要比类数组要高很多，因此如果在遇到有遍历类数组的需求的时候（比如遍历一个NodeList集合中的所有元素），建议先将类数组转化成数组，在执行遍历以此优化性能。

数组中给出了很多已有的方法方便我们对数组进行增、删、改、查等操作，比如常用的数组追加方法Array.push()，
类数组就不存在push这个方法，事实上，除了上文中所说的几个相同地方，数组中包含的用以操作数组的方法类数组都不存在，所以说，类数组毕竟是类数组，它终究不是数组啊。

返回值：
precision：n维数组（形状=n_thresholds + 1,)
精度值，其中元素i是预测的精度得分>=阈值[i]，最后一个元素是1。

recall：n维数组（形状=n_thresholds + 1,)
递减召回值，使元素i是预测的召回值得分>=阈值[i]的，最后一个元素是0。

thresholds：n维数组（形状=n_thresholds,)
增加用于计算精度和召回率的决策函数的阈值，其中n_thresholds = len(np.unique(probas_pred))。

sklearn.metrics.precision_recall_curve(y_true, probas_pred, *, pos_label=None, sample_weight=None)

import numpy as np
from sklearn.metrics import precision_recall_curve
y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
precision, recall, thresholds = precision_recall_curve(
...     y_true, y_scores)
precision
# array([0.5       , 0.66666667, 0.5       , 1.        , 1.        ])
recall
# array([1. , 1. , 0.5, 0.5, 0. ])
thresholds
# array([0.1 , 0.35, 0.4 , 0.8 ])

2.6 F1 Score
（1）理论及适用条件
通常情况下，Precision和Recall是相互影响的，Precision高、Recall 就低；Recall 高、Precision就低。那么有没有一个能够衡量这两个指标的方法呢？所以这里就引出了F1 Score。F1函数是一个常用指标，F1值是精确率和召回率的调和均值：
$$F1=\frac{2}{\frac{1}{precision}+\frac{1}{recall}}$$
或者
$$F1=\frac{2\ast precision\ast recall}{precision+recall}$$

可以看到，当Recall或者Precision的值很小的时候，F值也将很小，因此不管其中一个值多高，只要另一个值很小，F就会很小。Precision和Recall对F1的贡献是相同的。

在多类和多标签的情况下，这是每一类的F1得分的平均值，其权重取决于平均参数。

（2）如何用sklearn包计算F1 Score
我们可以使用sklearn包下面的metrics模块里面的函数“f1_score”：
sklearn.metrics.f1_score(y_true, y_pred, *, labels=None, pos_label=1, average=‘binary’, sample_weight=None, zero_division=‘warn’)

参数：

参数名	含义	形式
y_true	正确标签	一维类数组，或标签指示数组/稀疏矩阵（0比1多即为稀疏）
y_pred	分类器预测的标签	一维类数组，或标签指示数组/稀疏矩阵
average	对于多分类/多标签的情况下，此参数是必需的。**如果为None，则返回每个类的分数。**否则，将按照指定“average”的方法来对数据集进行处理。------binary：仅报告由pos_label指定的类的结果，（y_ {true,pred}）为二进制时才适用----‘micro’:通过计算总的TP、FN和FP来整体计算指标---- ‘macro’：计算每个标签的未加权均值（不考虑不平衡）。----‘samples’:计算每个实例找出其均值（仅对多标签分类有意义，这与 accuracy_score 不同）。—‘weighted’:计算每个标签的加权均值（每个标签的真实实例数），与macro相比，考虑了不平衡，它可能导致 F 分数不在精确率和召回率之间。	{‘micro’, ‘macro’, ‘samples’, ‘weighted’, ‘binary’} or None, default=’binary’
labels	当average！='binary’时所包含的一组标签，如果average是None，则为标签的顺序。数据中存在的标签可以被排除，例如，可以忽略多数negative类来计算多类average。当标签不存在数据中时，将导致average=“macro” 时出现0组成。对于多标签目标，标签是列索引。 默认情况下，y_true和y_pred中的所有标签均按排序的顺序使用。	类似数组的，default=None
pos_label	如果average='binary’并且数据是binary，报告分类。如果数据是多分类或者多标签的，则将被忽略。设置labels=[pos_label]和 average != ‘binary’，将仅仅报告标签的分数。	str or int, default=1
zero_division	当有除0错误的时候设置返回的值。如果设置为“ warn”，则该值为0，但也会发出警告。	“warn”, 0 or 1, default=”warn”

返回值：
f1_score：浮点数或浮点数的数组，shape = [n_unique_labels]

二元分类中阳性类的F1得分或多类任务中各类F1得分的加权平均。

from sklearn.metrics import f1_score
y_true = [0, 1, 2, 0, 1, 2]
y_pred = [0, 2, 1, 0, 0, 1]
f1_score(y_true, y_pred, average='macro')
0.26...
f1_score(y_true, y_pred, average='micro')
0.33...
f1_score(y_true, y_pred, average='weighted')
0.26...
f1_score(y_true, y_pred, average=None)
array([0.8, 0. , 0. ])
y_true = [0, 0, 0, 0, 0, 0]
y_pred = [0, 0, 0, 0, 0, 0]
f1_score(y_true, y_pred, zero_division=1)
1.0...
# multilabel classification
y_true = [[0, 0, 0], [1, 1, 1], [0, 1, 1]]
y_pred = [[0, 0, 0], [1, 1, 1], [1, 1, 0]]
f1_score(y_true, y_pred, average=None)
array([0.66666667, 1.        , 0.66666667])

2.7 ROC Curve和Area under Curve （AUC）
（1）理论及适用条件
定义：ROC曲线，全称是“受试者工作特征”(Receiver Operating Characteristic)曲线。以“真正例率”(True Positive Rate, TPR)为纵轴，“假正例率”(False Positive Rate, FPR)为横轴。
$$TPR=\frac{TP}{TP+FN}$$
$$FPR=\frac{FP}{FP+TN}$$

$$precision=\frac{TP}{TP+FP}$$
$$recall=\frac{TP}{TP+FN}$$

在众多的机器学习模型中，很多模型输出的是预测概率，而使用精确率、召回率这类指标进行模型评估时，还需要对预测概率设分类阈值，比如预测概率大于阈值为正例，反之为负例。这使得模型多了一个超参数，并且这超参数会影响模型的泛化能力。

ROC曲线不需要设定这样的阈值，与PR曲线类似，ROC曲线考虑了给定分类器的所有可能的阈值，但它显示的是“假正例率（false positive rate，FPR）和“真正例率”（true positive rate，TPR）之间的关系，而不是报告precision和recall。回想一下，真正率只是recall的另一个名称，而假正例率则是假正例占所有反类样本的比例。

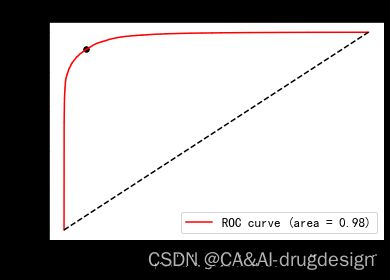
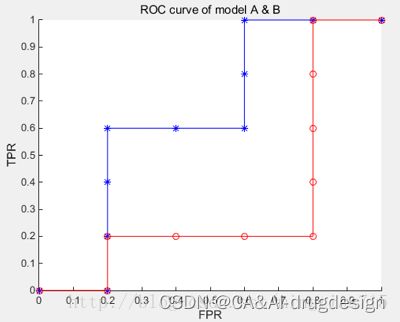
ROC（Receiver Operating Characteristic）曲线常用来评价一个二值分类器的优劣，理想的曲线要靠近左上角：你希望分类器的recall很高，同时保持假正率很低。上图所示的点表明，在该阈值下，我们可以得到明显更高recall，而仅仅稍微增加FPR。一般最接近左上角的点可能是比默认选择（比如默认阈值0）更好的工作点。同样请注意，不应该在测试集上选择阈值，而是应该在单独的验证集上选择。

图中蓝色为学习器A的ROC曲线，其包含了B的曲线，说明它性能更优秀，这点从A,B对10个例子的排序结果显然是能看出来的，A中正例排序高的数目多于B。此外，如果两个曲线有交叉，则需要计算曲线围住的面积(AUC)来评价性能优劣。

与PR曲线一样，我们希望使用一个数字来总结ROC曲线，即AUC(Area Under Curve)：ROC曲线下的面积。AUC能很好地描述模型整体性能的高低。无论数据集中的类别多么不平衡，随机预测得到的AUC总是等于0.5。对于不平衡的分类问题来说，AUC是一个比精度好得多的指标。 AUC可以解释为评估正例样本的排名，它等价于从正类样本中随机挑选一个点，由分类器给出的分数比从反类样本中随机挑选一个点的分数更高的概率。因此，AUC最高为1，这说明所有正类点的分数高于所有反类点。

适用条件：
强烈建议在不平衡数据集上评估模型时使用AUC。但请记住，AUC没有使用默认阈值，因此，为了从高AUC的模型中得到有用的分类结果，可能还需要调节决策阈值。

（2）如何用sklearn包计算ROC Curve和AUC
我们可以使用sklearn包下面的metrics模块里面的函数“roc_curve”：
sklearn.metrics.roc_curve(y_true, y_score, *, pos_label=None, sample_weight=None, drop_intermediate=True)

参数：

参数名	含义	形式
y_true	真正的二进制标签。如果标签不是{-1，1}或{0，1}，那么应该明确给出pos_label。	n维数组 (shape=n_samples,)
y_score	目标分数，可以是正类的概率估计，也可以是置信值，或者是决策的非阈值测量（如某些分类器上的 "decision_function "所返回）。	n维数组 (shape=n_samples,)
pos_label	正类的标签。当pos_label=None时，如果y_true在{-1，1}或{0，1}中，pos_label被设置为1，否则将产生错误。	str or int, default=1
sample_weight	样品权重	类数组（shape=n_samples,）, default=None
drop_intermediate	可选择去掉一些对于ROC性能不利的阈值,使得得到的曲线有更好的表现性能	布尔值, default=True

返回值：
fpr：n维数组 (shape>2,)
递增假阳性率，这样元素i是预测的假阳性率，得分>=阈值[i]。

tpr：n维数组 (shape>2,)
递增真阳性率，这样元素i是预测的真阳性率，得分>=阈值[i]。

阈值：n维数组（shape = n_thresholds,）
用于计算fpr和tpr的决策函数的递减阈值。阈值[0]代表没有被预测的实例，并被任意设置为max(y_score) + 1。

import numpy as np
from sklearn import metrics
y = np.array([1, 1, 2, 2])
scores = np.array([0.1, 0.4, 0.35, 0.8])
fpr, tpr, thresholds = metrics.roc_curve(y, scores, pos_label=2)
fpr
array([0. , 0. , 0.5, 0.5, 1. ])
tpr
array([0. , 0.5, 0.5, 1. , 1. ])
thresholds
array([1.8 , 0.8 , 0.4 , 0.35, 0.1 ])

我们可以使用sklearn包下面的metrics模块里面的函数“roc_auc_score”：
sklearn.metrics.roc_auc_score(y_true, y_score, *, average=‘macro’, sample_weight=None, max_fpr=None, multi_class=‘raise’, labels=None)

参数：

参数名	含义	形式
y_true	真正的标签或二进制标签指标。二元和多类的情况下，希望标签的形状是（n_samples,），而多标签的情况下，希望二元标签指标的形状是（n_samples, n_classes）。	类数组（shape=n_samples,）或or (shape=n_samples, n_classes)
y_score	在二分类情况下，它对应于一个形状的数组（n_samples，）。在多分类情况下，它对应于由predict_proba方法提供的概率估计的形状（n_samples, n_classes）的数组。	类数组，shape= (n_samples,) or (n_samples, n_classes)
average	如果为None，则返回每个类的分数。 否则，这决定了对数据进行的平均化类型。注意：多类ROC AUC目前只处理 "宏观 "和 "加权 "平均数。对于多类目标，average=None只在multi_class='ovo’时实现。否则，将按照指定“average”的方法来对数据集进行处理。---- ‘micro’：通过将标签指标矩阵的每个元素视为一个标签，在全局上计算度量。---- ‘macro’：计算每个标签的度量，并找到它们的非加权平均值。这并不考虑标签的不平衡性。----‘samples’:计算每个实例找出其均值（仅对多标签分类有意义，这与 accuracy_score 不同）。—‘weighted’:计算每个标签的度量，并找到它们的平均值，按支持度（每个标签的真实实例数）加权。	{‘micro’, ‘macro’, ‘samples’, ‘weighted’} or None, default=’macro’
max_fpr	如果不是NONE，将返回[0, max_fpr]范围内的标准化部分AUC。对于多类情况，max_fpr，应该等于无或1.0，因为AUC ROC部分计算目前不支持多类。	float > 0 and <= 1, default=None
sample_weight	样品权重	类数组（shape=n_samples,）, default=None
multi_class	只用于多类目标。确定要使用的配置类型。默认值会引发错误，所以必须明确传递’ovr’或’ovo’。----‘ovr’: 代表One-vs-rest。计算每个类别对其他类别的AUC。这与多标签情况下处理多类情况的方式相同。即使在average == 'macro’的情况下，对类的不平衡也很敏感，因为类的不平衡会影响每个’rest’分组的组成。。----‘ovo’: 代表One-vs-one。计算所有可能的类对组合的平均AUC。当average == 'macro’时，对类的不平衡不敏感。	{‘raise’, ‘ovr’, ‘ovo’}, default=’raise’

返回值：
auc：float
Area Under the Curve score.

**# Binary case:**
from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score
X, y = load_breast_cancer(return_X_y=True)
clf = LogisticRegression(solver="liblinear", random_state=0).fit(X, y)
roc_auc_score(y, clf.predict_proba(X)[:, 1])
0.99...
roc_auc_score(y, clf.decision_function(X))
0.99...

# Multiclass case:
from sklearn.datasets import load_iris
X, y = load_iris(return_X_y=True)
clf = LogisticRegression(solver="liblinear").fit(X, y)
roc_auc_score(y, clf.predict_proba(X), multi_class='ovr')
0.99...

# Multilabel case:
import numpy as np
from sklearn.datasets import make_multilabel_classification
from sklearn.multioutput import MultiOutputClassifier
X, y = make_multilabel_classification(random_state=0)
clf = MultiOutputClassifier(clf).fit(X, y)
# get a list of n_output containing probability arrays of shape
# (n_samples, n_classes)
y_pred = clf.predict_proba(X)
# extract the positive columns for each output
y_pred = np.transpose([pred[:, 1] for pred in y_pred])
roc_auc_score(y, y_pred, average=None)
array([0.82..., 0.86..., 0.94..., 0.85... , 0.94...])
from sklearn.linear_model import RidgeClassifierCV
clf = RidgeClassifierCV().fit(X, y)
roc_auc_score(y, clf.decision_function(X), average=None)
array([0.81..., 0.84... , 0.93..., 0.87..., 0.94...])

2.8 Matthews correlation coefficient (MCC)
（1）理论及适用条件
马休斯相关系数是衡量二分类模型结果的评估指标之一，具体参考Matthews Correlation Coefficient is The Best Classification Metric You’ve Never Heard Of，它能解决不均衡类别数据的指标衡量问题。

由precision、recall、F1的计算公式可以看出这三个指标完全与TN无关，只关心正类而忽略了负类的表现。而当类别不平衡时ACC的评估指标无法关注到少数类。

为了解决这个问题，可以将prediction与真实结果看为两个0-1分布，然后用马修斯相关系数衡量两个分布的相似性，马修斯相关系数的计算公式如下：
$$Matthews-score(MCC)=\frac{TP\ast TN-FP\ast FN}{\sqrt{\left(TP+FP\right)\left(FN+TP\right)\left(FN+TN\right)\left(FP+TN\right)}}$$

• 当FP=FN=0即完全预测正确时 MCC=1
• 当完全预测错误时MCC=-1，此时将标签逆转即可
• 当MCC=0时表明模型不比随机预测好

（2）如何用sklearn包计算MCC
我们可以使用sklearn包下面的metrics模块里面的函数“matthews_corrcoef”：
sklearn.metrics.matthews_corrcoef(y_true, y_pred, *, sample_weight=None)

参数：

参数名	含义	形式
y_true	真正的分类	数组, shape = [n_samples]
y_pred	分类器预测的分类	数组, shape = [n_samples]
sample_weight	权重	类数组（shape=n_samples, default=None）

返回值：
mcc：float
马修斯相关系数（+1代表完美预测，0代表平均随机预测，-1代表逆向预测）。

from sklearn.metrics import matthews_corrcoef
y_true = [+1, +1, +1, -1]
y_pred = [+1, -1, +1, +1]
matthews_corrcoef(y_true, y_pred)
-0.33...

3. 不同评价指标适合的情境总结

指标	适用条件
Confusion Matrix（混淆矩阵）	该布局使得算法的性能可视化，通常适用于监督学习算法（在无监督学习中，它通常被称为匹配矩阵）。 以下其他分类模型的评价指标均为基于混淆矩阵的拓展指标。
Accuracy（ACC）	该布局使得算法的性能可视化，通常适用于监督学习算法（在无监督学习中，它通常被称为匹配矩阵）。 以下其他分类模型的评价指标均为基于混淆矩阵的拓展指标。
Recall	正确分类的正例个数占实际正例个数的比例，也称查全率或召回率。用于直观地表示分类器找到所有正样本的能力。如果我们关心“所有好瓜中有多少比例被挑出来”，就可以使用recall。precision通常与recall一起使用。precision与recall是一对矛盾的度量，一般来说，precision高时，recall低；recall高时，precision低。通常只有在一些简单任务中，才可能使查全率和查准率都很高，也就是FP（假阳）和FN（假阴）都比较低。
PR Curve	在开发新模型时，通常并不完全清楚工作点在哪里。因此，为了更好地理解建模问题，很有启发性的做法是，同时查看所有可能的阈值或准确率和召回率的所有可能折中。利用一种叫准确率-召回率曲线（precision-recall curve）的工具可以做到这一点。
F1 Score	F1值是精确率和召回率的调和均值。当Recall或者Precision的值很小的时候，F值也将很小，因此不管其中一个值多高，只要另一个值很小，F就会很小。Precision和Recall对F1的贡献是相同的。
ROC Curve和Area under Curve （AUC）	ROC（Receiver Operating Characteristic）曲线常用来评价一个二值分类器的优劣。与PR曲线一样，我们希望使用一个数字来总结ROC曲线，即AUC(Area Under Curve)：ROC曲线下的面积。AUC能很好地描述模型整体性能的高低。无论数据集中的类别多么不平衡，随机预测得到的AUC总是等于0.5。对于不平衡的分类问题来说，AUC是一个比精度好得多的指标。AUC可以解释为评估正例样本的排名，它等价于从正类样本中随机挑选一个点，由分类器给出的分数比从反类样本中随机挑选一个点的分数更高的概率。
Matthews correlation coefficient (MCC)	马休斯相关系数是衡量二分类模型结果的评估指标之一，它能解决不均衡类别数据的指标衡量问题。由precision、recall、F1的计算公式可以看出这三个指标完全与TN无关，只关心正类而忽略了负类的表现。而当类别不平衡时ACC的评估指标无法关注到少数类。为了解决这个问题，可以将prediction与真实结果看为两个0-1分布，然后用马修斯相关系数衡量两个分布的相似性。

参考资料：

1. 机器学习，周志华
2. https://blog.csdn.net/lmx_smile/article/details/107078802
3. https://blog.csdn.net/wxplol/article/details/93471838?spm=1001.2014.3001.5506
4. https://towardsdatascience.com/metrics-to-evaluate-your-machine-learning-algorithm-f10ba6e38234
5. https://blog.csdn.net/YW_Vine/article/details/120779712
6. https://editor.codecogs.com/
7. https://scikit-learn.org/stable/modules/classes.html#sklearn-metrics-metrics
8. https://klmav.cuc.edu.cn/2019/0601/c2286a125166/page.htm
9. http://www.360doc.com/content/21/0721/22/7673502_987640712.shtml
   10.https://www.analyticsvidhya.com/blog/2019/08/11-important-model-evaluation-error-metrics/
10. https://scikit-learn.org/stable/modules/model_evaluation.html#precision-recall-f-measure-metrics
11. https://www.imooc.com/article/48944
12. Python机器学习基础教程