HBU_神经网络与深度学习 实验1 numpy

注：

1. 本文为HBU_神经网络与深度学习实验（2022年秋）实验1的实验报告，此文对模板 NNDL 实验一 numpy_HBU_David的博客-CSDN博客 的一部分进行了格式修改，故题干描述可能略有不同，检索时请按对应题号进行检索。
2. 本实验编程语言为Python 3.
3. 水平有限，如有错误之处敬请指正。

一、numpy的array操作

1. 导入numpy库.

import numpy as np

2. 建立一个一维数组 a，初始化为[4,5,6].

（1）输出 a 的类型（type）;

（2）输出 a 的各维度的大小（shape）;

（3）输出 a 的第一个元素（值为4）.

a = np.array([4,5,6])
print(type(a))
print(a.shape)
print(a[0])

代码执行结果：

<class 'numpy.ndarray'>
(3,)
4

调用shape可输出array的长度。

3. 建立一个二维数组 b，初始化为[[4, 5, 6], [1, 2, 3]].

（1）输出各维度的大小（shape）;

（2）输出 b(0,0), b(0,1), b(1,1) 这三个元素（对应值分别为4, 5, 2）.

b = np.array([[4,5,6], [1,2,3]])
print(b.shape)
print(b[0,0])
print(b[0,1])
print(b[1,1])
'''print(b[[0,0,1],[0,1,1]]'''

代码执行结果：

(2, 3)
4
5
2

[4,5,2]

4.（1）建立一个全 0 矩阵 a，大小为 3x3, 类型为整型;（提示：dtype = int）

（2）建立一个全 1 矩阵 b，大小为 4x5;

（3）建立一个单位矩阵 c，大小为 4x4;

（4）生成一个随机数矩阵 d，大小为 3x2.

a = np.zeros((3,3), dtype=int)
b = np.ones((4,5), dtype=int)
c = np.identity(4)
d = np.random.randn(3,2)
print(a)
print(b)
print(c)
print(d)

代码执行结果：

[[0 0 0]
 [0 0 0]
 [0 0 0]]
[[1 1 1 1 1]
 [1 1 1 1 1]
 [1 1 1 1 1]
 [1 1 1 1 1]]
[[1. 0. 0. 0.]
 [0. 1. 0. 0.]
 [0. 0. 1. 0.]
 [0. 0. 0. 1.]]
[[-0.03045403 -0.48254898]
 [-0.22414438 -0.82975705]
 [-0.88671865 -0.3147889 ]]

5. 建立一个数组 a，值为[[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]].

（1）打印 a;

（2）输出下标为 (2,3), (0,0) 这两个数组元素的值.

a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
print(a)
print(a[2][3], a[0][0])

代码执行结果：

[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]
12 1

6. 把上一题的 a 数组的 0 到 1 行和 2 到 3 列放到 b 里面去.（此处不需要从新建立 a，直接调用即可）

（1）输出 b;

（2）输出 b 中 (0,0) 这个元素的值.

b = a[0:2,1:3]
print(b)
print(b[0][0])

代码执行结果：

[[2 3]
 [6 7]]
2

7. 把第 5 题中数组 a 的最后两行所有元素放到 c 中.（提示：a[1:2, :]）

（1）输出 c;

（2）输出 c 中第一行的最后一个元素.（提示：使用 -1 表示最后一个元素）

c = a[1:3,:]
print(c)
print(c[0][-1])

代码执行结果：

[[ 5  6  7  8]
 [ 9 10 11 12]]
8

8. 建立数组 a，初始化为[[1, 2], [3, 4], [5, 6]]，输出 (0,0), (1,1), (2,0) 这三个元素. （提示：使用 print(a[[0, 1, 2], [0, 1, 0]])）

a = np.array([[1,2], [3,4], [5,6]])
print(a[[0,1,2], [0,1,0]])

代码执行结果：

[1 4 5]

通过多个元素在矩阵的行列位置可以返回多个数值。

9. 建立矩阵 a，初始化为[[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]]，输出 (0,0), (1,2), (2,0), (3,1).

（提示：使用 b = np.array([0, 2, 0, 1]), print(a[np.arange(4), b])）

a = np.array([[1,2,3], [4,5,6], [7,8,9], [10,11,12]])
b = np.array([0,2,0,1])
print(a[np.arange(4),b])

代码执行结果：

[ 1  6  7 11]

10. 对第 9 题中输出的四个元素各加上 10，然后重新输出矩阵 a. (提示：a[np.arange(4), b] += 10）

a[np.arange(4),b] += 10
print(a[np.arange(4),b])

代码执行结果：

[11 16 17 21]

二、array 的数学运算

11. 执行 x = np.array([1, 2])，然后输出 x 的数据类型.

x = np.array([1, 2])
print(x.dtype)

代码执行结果：

int32

12. 执行 x = np.array([1.0, 2.0])，然后输出 x 的数据类型.

x = np.array([1.0, 2.0])
print(x.dtype)

代码执行结果：

float64

13. 执行 x = np.array([[1, 2], [3, 4]], dtype=np.float64), y = np.array([[5, 6], [7, 8]], dtype=np.float64)，然后输出 x+y 和 np.add(x,y)

x = np.array([[1, 2], [3, 4]], dtype=np.float64)
y = np.array([[5, 6], [7, 8]], dtype=np.float64)
print(x+y)
print(np.add(x,y))

代码执行结果：

[[ 6.  8.]
 [10. 12.]]
[[ 6.  8.]
 [10. 12.]]

两者的计算方式相同，均为方阵中各对应位置相加。

14. 利用第 13 题中的 x, y 输出 x-y 和 np.subtract(x,y)

print(x-y)
print(np.subtract(x,y))

代码执行结果：

[[-4. -4.]
 [-4. -4.]]
[[-4. -4.]
 [-4. -4.]]

两者的计算方式相同，均为方阵中各对应位置相减。

15. 利用第 13 题中的 x, y 输出 x*y , np.multiply(x, y) 和 np.dot(x,y) 并比较三者差异，然后自己换一个不是方阵的试试.

print(x*y)
print(np.multiply(x,y))
print(np.dot(x,y))

代码执行结果：

[[ 5. 12.]
 [21. 32.]]
[[ 5. 12.]
 [21. 32.]]
[[19. 22.]
 [43. 50.]]

将矩阵改为非方阵

x = np.array([[1, 2, 3], [4, 5, 6]], dtype=np.float64)
y = np.array([[7, 8, 9], [10, 11, 12]], dtype=np.float64)
'''y = np.array([[7, 8],[9, 10], [11, 12]], dtype=np.float64)'''
print(x*y)
print(np.multiply(x,y))
'''print(np.dot(x,y))'''

代码执行结果：

[[ 7. 16. 27.]
 [40. 55. 72.]]
[[ 7. 16. 27.]
 [40. 55. 72.]]

[[ 58.  64.]
 [139. 154.]]

x*y和np.multiply(x, y)需要x和y的行列数一致，np.dot(x,y)需要x的列数和y的行数一致。

16. 利用第 13 题中的 x, y 输出 x/y.（提示：使用函数 np.divide()）

print(x/y)
print(np.divide(x,y))

代码执行结果：

[[0.2        0.33333333]
 [0.42857143 0.5       ]]
[[0.2        0.33333333]
 [0.42857143 0.5       ]]

两者的计算方式相同，均为方阵中各对应位置相除。

17. 利用第 13 题中的 x 输出 x 的开方.（提示：使用函数 np.sqrt()）

x = np.array([[1, 2], [3, 4]], dtype=np.float64)
y = np.array([[5, 6], [7, 8]], dtype=np.float64)
print(np.sqrt(x))

代码执行结果：

[[1.         1.41421356]
 [1.73205081 2.        ]]

18. 利用第 13 题中的 x, y 执行 print(x.dot(y)) 和 print(np.dot(x,y)).

print(x.dot(y))
print(np.dot(x,y))

代码执行结果：

[[19. 22.]
 [43. 50.]]
[[19. 22.]
 [43. 50.]]

两种调用方式的计算结果相同。

19. 利用第 13 题中的 x 进行求和.

（提示：输出三种求和 (1)print(np.sum(x)); (2)print(np.sum(x,axis = 0)); (3)print(np.sum(x,axis = 1))

print(np.sum(x))
print(np.sum(x,axis = 0))
print(np.sum(x,axis = 1))

代码执行结果：

10.0
[4. 6.]
[3. 7.]

axis=0表示各行元素分别相加，axis=1表示各列元素分别相加。

20. 利用第 13 题中的 x 进行求平均数.

（提示：输出三种平均数(1) print(np.mean(x)); (2) print(np.mean(x,axis = 0)); (3) print(np.mean(x,axis = 1))）

print(np.mean(x))
print(np.mean(x,axis = 0))
print(np.mean(x,axis = 1))

代码执行结果：

2.5
[2. 3.]
[1.5 3.5]

此题中，axis所代表的内容与19题一致。

21. 利用第 13 题中的 x 对 x 进行矩阵转置，然后输出转置后的结果.（提示：x.T 表示对 x 的转置）

print(x.T)

代码执行结果：

[[1. 3.]
 [2. 4.]]

22. 利用第 13 题中的 x 求 e 的指数.（提示：函数 np.exp()）

print(np.exp(x))

代码执行结果：

[[ 2.71828183  7.3890561 ]
 [20.08553692 54.59815003]]

23. 利用第 13 题中的 x 求值最大的下标.

（提示：(1) print(np.argmax(x)); (2) print(np.argmax(x, axis =0)); (3) print(np.argmax(x),axis = 1)）

print(np.argmax(x))
print(np.argmax(x, axis = 0))
print(np.argmax(x, axis = 1))

代码执行结果：

3
[1 1]
[1 1]

此题中，axis所代表的内容与19题一致。

三、matplotlib在numpy中的简单应用

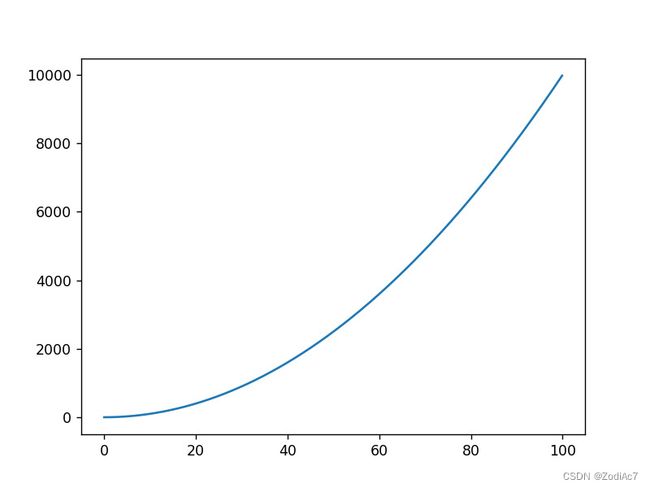
24. 画图 y=x*x，其中 x = np.arange(0, 100, 0.1) .

（提示：这里用到 matplotlib.pyplot 库）

import matplotlib.pyplot as plt

x = np.arange(0, 100, 0.1)
y = x * x
plt.plot(x, y)
plt.show()

代码执行结果如下图所示：

25. 画图。画正弦函数和余弦函数 x = np.arange(0, 3 * np.pi, 0.1).

（提示：这里用到 np.sin() np.cos() 函数和 matplotlib.pyplot 库）

x = np.arange(0, 3 * np.pi, 0.1)
y = np.sin(x)
z = np.cos(x)
plt.plot(x, y)
plt.plot(x, z)
plt.show()

代码执行结果如下图所示：
​

四、实验总结

本次实验的主要目的是回忆Python中numpy包的用法及其简单应用，通过本次实验我们可以对旧有课程的学习内容进行复习，为日后的神经网络与深度学习巩固基础。