Sobel边缘检测 - 梯度算子介绍
边缘检测简介
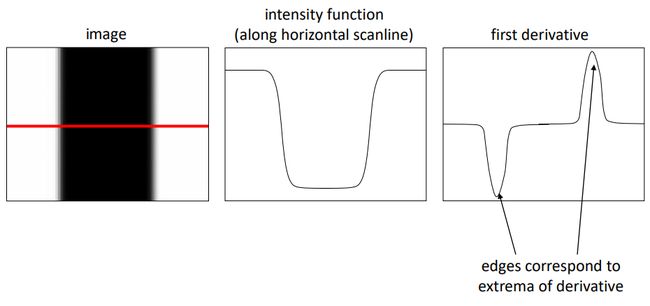
边缘检测,简单说就是找出图像突变的地方,如上图所示。
图像微分简介
图像微分是一种简单情况的离散微分。
离散微分
连续微分是微积分的基本内容,实际离散微分概念也是类似,在微积分发明前就有了。
微分定义
d f d x = f ( x 2 ) − f ( x 1 ) ∣ x 2 − x 1 ∣ \frac{df}{dx} = \frac{f(x_2) - f(x_1)}{|x_2 - x_1|} dxdf=∣x2−x1∣f(x2)−f(x1)
d f d x = f ( x ) − f ( x − 1 ) = f ′ ( x ) Backward difference \frac{df}{dx}=f(x ) - f(x - 1) = f'(x) \quad \text{Backward difference} dxdf=f(x)−f(x−1)=f′(x)Backward difference
d f d x = f ( x ) − f ( x + 1 ) = f ′ ( x ) Forward difference \frac{df}{dx}=f(x ) - f(x + 1) = f'(x) \quad \text{Forward difference} dxdf=f(x)−f(x+1)=f′(x)Forward difference
d f d x = f ( x + 1 ) − f ( x − 1 ) 2 = f ′ ( x ) Central difference \frac{df}{dx}=\frac{f(x + 1) - f(x - 1)}{2} = f'(x) \quad \text{Central difference} dxdf=2f(x+1)−f(x−1)=f′(x)Central difference
容易看出 ( x + 1 ) − ( x − 1 ) = 2 (x + 1) - (x - 1) = 2 (x+1)−(x−1)=2, Central differnce 要除以 2 2 2
图像微分和梯度(gradient)
图像偏微分也是类似的,下面只介绍最常用的Central difference。
∂ f ∂ x = f ( x + 1 , y ) − f ( x − 1 , y ) 2 \frac{\partial f}{\partial x} = \frac{f(x + 1, y) - f(x - 1, y)}{2} ∂x∂f=2f(x+1,y)−f(x−1,y)
∂ f ∂ y = f ( x , y + 1 ) − f ( x , y − 1 ) 2 \frac{\partial f}{\partial y} = \frac{f(x, y + 1) - f(x, y - 1)}{2} ∂y∂f=2f(x,y+1)−f(x,y−1)
图像梯度
∇ f = ( ∂ f ∂ x , ∂ f ∂ y ) \nabla f = (\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}) ∇f=(∂x∂f,∂y∂f)
这是一个2D 向量(vector)。
Sobel 算子
Sobel X方向算子
G x = [ − 1 0 + 1 − 2 0 + 2 − 1 0 + 1 ] G_x = \begin{bmatrix} -1 & 0 & +1 \\ -2 & 0 & +2 \\ -1 & 0 & + 1 \end{bmatrix} Gx=⎣⎡−1−2−1000+1+2+1⎦⎤
Sobel Y方向算子
G y = [ − 1 − 2 − 1 0 0 0 + 1 + 2 + 1 ] G_y = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ +1 & +2 & +1 \end{bmatrix} Gy=⎣⎡−10+1−20+2−10+1⎦⎤
这个里给出算子的和有些文献为什是反的, 因为上面算子是 互相关联(cross-correlation), 而有的文献是给的是卷积(convolution), 卷积刚好是把互相关联 旋转了 18 0 ∘ 180^{\circ} 180∘,这里不详细讨论了。可以参考 Correlation and Convolution - David Jacobs。
Sobel 做边缘检测过程
先将Image 用 G x G_x Gx和 G y G_y Gy分别过滤得到过滤后的图像 G x ′ G'_x Gx′和 G y ′ G'_y Gy′。
G ′ = ( G x ′ , G y ′ ) G'=(G'_x, G'_y) G′=(Gx′,Gy′)
G ′ G' G′被称作梯度(Gradient), 这个梯度的长度是 ∣ G ′ ∣ = ( G x ′ ) 2 + ( G y ′ ) 2 |G'|=\sqrt{(G'_x)^2 + (G'_y)^2} ∣G′∣=(Gx′)2+(Gy′)2
这个梯度方向的角度 Θ = a t a n 2 ( G y ′ , G x ′ ) \Theta = \mathrm{atan2}(G'_y, G'_x) Θ=atan2(Gy′,Gx′)
假定一个阈值 T T T, 如果 ∣ G ′ ∣ 2 > T |G'|^2 > T ∣G′∣2>T,那么那个像素就是边缘。
Sobel 公式的由来
Sobel的梯度计算,只涉及3x3像素范围
a b c d e f g h i \begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \end{array} adgbehcfi
对应像素坐标
[ 0 , 0 ] [ 1 , 0 ] [ 2 , 0 ] [ 0 , 1 ] [ 1 , 1 ] [ 2 , 1 ] [ 0 , 2 ] [ 1 , 2 ] [ 2 , 2 ] \begin{array}{ccc} [0,0] & [1,0] & [2,0]\\ [0,1] & [1,1] & [2,1] \\ [0,2] & [1,2] & [2,2] \end{array} [0,0][0,1][0,2][1,0][1,1][1,2][2,0][2,1][2,2]
这
(x轴向右,y轴向下)
从微分公式可以容易看出,梯度向量的长度
∣ ∇ F ∣ = (density difference) / (distance to neighbor) |\nabla F| = \text{(density difference)}/\text{(distance to neighbor)} ∣∇F∣=(density difference)/(distance to neighbor)
假定图像是密度函数(density function)
Sobel实际是 左右,上下,主对角线( a i ai ai),副对角线( c g cg cg)方向微分的向量和。
比较容易看出 x x x方向单位向量是 [ 1 , 0 ] [1, 0] [1,0], y y y方向单位向量 [ 0 , 1 ] [0, 1] [0,1], 主对角线向量 [ 1 , 1 ] [1, 1] [1,1], 副对角线向量 [ − 1 , 1 ] [-1, 1] [−1,1]。
这个就是Sobel给出的公式,实际是个近似公式,x, y 方向没问题。主对角线和副对角线向量不是单位向量,这两个向量像素的距离是曼哈坦距离( Manhattan Distance),不是欧几里得距离(Euclidean Distance), x, y 方向曼哈坦距离和欧几里得距离都是一样的
a a a的像素坐标 [ 0 , 0 ] [0, 0] [0,0], b b b的像素坐标 [ 1 , 0 ] [1, 0] [1,0],依次类推,不再每一个列举出来。
假设 d d d是曼哈坦距离函数
d ( M , P ) ≡ ∣ M x − P x ∣ + ∣ M y − P y ∣ d(M,P) \equiv |M_x-P_x|+|M_y-P_y| d(M,P)≡∣Mx−Px∣+∣My−Py∣
d f ⃗ = [ 2 , 1 ] − [ 0 , 1 ] = [ 2 , 0 ] \vec{df} = [2, 1] - [0, 1] = [2, 0] df=[2,1]−[0,1]=[2,0], d ( d f ⃗ ) = 2 d(\vec{df}) = 2 d(df)=2
b h ⃗ = [ 1 , 2 ] − [ 1 , 0 ] = [ 0 , 2 ] \vec{bh}=[1,2] - [1,0]=[0, 2] bh=[1,2]−[1,0]=[0,2], d ( h d ⃗ ) = 2 d(\vec{hd}) = 2 d(hd)=2
a i ⃗ = [ 2 , 2 ] − [ 0 , 0 ] = [ 2 , 2 ] \vec{ai}=[2,2] - [0,0] = [2,2] ai=[2,2]−[0,0]=[2,2], d ( a i ⃗ ) = 4 d(\vec{ai}) = 4 d(ai)=4
c g ⃗ = [ 2 , 0 ] − [ 0 , 2 ] = [ 2 , − 2 ] \vec{cg}=[2,0] - [0,2] = [2,-2] cg=[2,0]−[0,2]=[2,−2], d ( c g ⃗ ) = 4 d(\vec{cg})=4 d(cg)=4
∇ F = ( f − d ) / 2 ∗ [ 1 , 0 ] + ( h − b ) / 2 ∗ [ 0 , 1 ] + ( i − a ) / 4 ∗ [ 1 , 1 ] + ( g − c ) / 4 ∗ [ − 1 , 1 ] = [ ( c − g − a + i ) / 4 + ( f − d ) / 2 , ( g − c − a + i ) / 4 + ( h − b ) / 2 ] \begin{aligned} \nabla F &= (f - d)/2 * [1, 0] \\ & + (h - b)/2 * [0, 1] \\ & + (i - a)/4 * [1,1] \\ & + (g - c)/4 * [-1,1] \\ &= [(c-g-a+i)/4 + (f-d)/2, (g-c-a+i)/4+(h-b)/2] \end{aligned} ∇F=(f−d)/2∗[1,0]+(h−b)/2∗[0,1]+(i−a)/4∗[1,1]+(g−c)/4∗[−1,1]=[(c−g−a+i)/4+(f−d)/2,(g−c−a+i)/4+(h−b)/2]
为了计算简便将分数去掉,那么乘以 4 4 4
G ′ = ∇ F ∗ 4 = [ c − g − a + i + 2 ∗ ( f − d ) , g − c − a + i + 2 ∗ ( h − b ) ] G'=\nabla F*4=[c-g-a+i + 2*(f-d), g-c-a+i+2*(h-b)] G′=∇F∗4=[c−g−a+i+2∗(f−d),g−c−a+i+2∗(h−b)]
a b c d e f g h i \begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \end{array} adgbehcfi
从上面的式子对照3x3的像素这个可以很容易算出
G x = [ − 1 0 + 1 − 2 0 + 2 − 1 0 + 1 ] G_x = \begin{bmatrix} -1 & 0 & +1 \\ -2 & 0 & +2 \\ -1 & 0 & + 1 \end{bmatrix} Gx=⎣⎡−1−2−1000+1+2+1⎦⎤
G y = [ − 1 − 2 − 1 0 0 0 + 1 + 2 + 1 ] G_y = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ +1 & +2 & +1 \end{bmatrix} Gy=⎣⎡−10+1−20+2−10+1⎦⎤
参考
- Correlation and Convolution - David Jacobs
- Digital Image Processing (3rd Edition)
- Finite Calculus: A Tutorial for Solving Nasty Sums - David Gleich
- History and Definition of the so-called “Sobel Operator”, more appropriately named the Sobel-Feldman Operator - Irwin Sobel