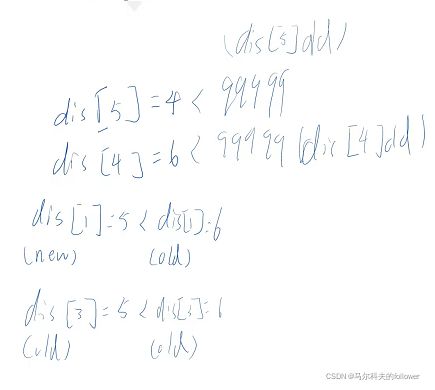Prim算法与Krusal算法代码实现,初学者友好型,非常简答
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
目录
文章目录
前言
一、prim算法的主要思想
二、具体
1.文字步骤
2.代码
一、Krusal算法的主要思想
二、文字步骤
三、代码:
总结
前言
提示:最近在学习这几个算法,非常简单,因为我就是新手。
1、在N条边的无向图的邻接表存储中,边表中结点的总数为(N)。
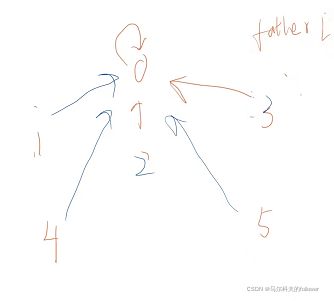
用普里姆(Prim)和克鲁斯卡尔算法给出图1的最小生成树(从0结点开始)
一、prim算法的主要思想
每次将距离集合点最小的边的所连的点纳入集合中
二、具体
1.文字步骤
Prim:
- 将节点设置为有三个变量的节点,一个num储存节点标号,一个distance储存节点到下一个节点的代价,一个储存有到下一个节点的指针。同时建立关联表。
- 会将已经遍历的节点装入一个集合S中,同时建立一个bool数组visited来判断节点是否在集合内。先将初始节点加入S中。
3.然后探索集合外代价最小的边,来探索未纳入的节点,所以还要有一个集合外的边集合来比较最小边是哪条,将每次最小边所连接的点纳入这个集合当中,distoblock存放着它到集合最短的距离。同时每个节点初始化distoblock每个节点为99999,视为无穷。
例:第一步遍历0号节点。
遍历6个节点到集合的距离,选取节点2,因为它到0的距离最短,所以将其视为下一个节点,同时visited【2】=true
第二步
探索节点2,这里的4与5节点都是未纳入的,距离肯定小于99999(我设置其为无限大),而,1与3也是未纳入的,但是已经在之前知道了1与3到集合S的距离,其存放在distoblock中。所以会进行比较后才放入。(其实4与5也有进行比较,其会与默认值99999进行比较)
遍历6个节点到集合的距离,选取节点5
接下来1,3,4的做法就和以上是一样的了。
4,重复3步骤,直到结束,获得最小生成树。
结果:
最小生成树是0-》2-》5-》3-》1-》4
2.代码
代码如下(示例):
#include
using namespace std;
typedef struct Vnode{
int num;
int distance;
struct Vnode *next;
}Vnode;
typedef Vnode Lgraph[6];
int n,e,disToBlock[6];
bool visited[6];
Lgraph Ga;//全局的数据表
void CreatGraph(Lgraph G){
Vnode *p,*q;
int i,j,k,d;
for(i=0;i<6;i++){
G[i].num=i;
G[i].next=NULL;
disToBlock[i]=99999;
}
for(k=1;k<=10;k++){
printf("请输入每条边的关联顶点编号和距离i,j,distance:");
scanf("%d,%d,%d",&i,&j,&d);
p=(Vnode *)malloc(sizeof(Vnode));
p->num=i;
p->next=G[j].next;
p->distance=d;
G[j].next=p;//下标i的节点的头结点为j
q=(Vnode *)malloc(sizeof(Vnode));
q->num=j;
q->next=G[i].next;
q->distance=d;
G[i].next=q;//下标j的节点的头结点为i
}
}
bool checkStop(bool *a){//查看每个节点是否被遍历过,都遍历过则返回true
bool canstop=true;
for(int i=0;i<6;i++)
if(a[i]==false) canstop=false;
return canstop;
}
void Prim(Lgraph G,int startPoint){
disToBlock[startPoint]=0;
visited[startPoint]=true;
Vnode *p=&Ga[startPoint];
while(!checkStop(visited)){
printf("访问节点%d\n",p->num);
Vnode *q=p->next;
while(q!=NULL){
if(visited[q->num]==false&&q->distancenum])
{
disToBlock[q->num]=q->distance;
printf("更新距离%d:%d\n",q->num,disToBlock[q->num]);
}
q=q->next;
}
int minDisInGraph=9999;
int minDisNode=0;
for(int i=0;i<6;i++){
if(visited[i]==false&&minDisInGraph>disToBlock[i]){
minDisInGraph=disToBlock[i];
minDisNode=i;
}
}
visited[minDisNode]=true;
p=&Ga[minDisNode];
}
printf("访问节点%d\n",p->num);
}
int main(){
printf("\n雷浩东 Prim算法\n");
CreatGraph(Ga);//初始化
Prim(Ga,0);//起点为0
return 0;
}
一、Krusal算法的主要思想
每次都寻找两个节点之间的最小边
二、文字步骤
- 将各个节点之间的信息构成一个集合edge,edge中存放着边与关联节点的信息。
同时构造并查集(这里确实需要去学一下并查集是什么才能继续往下看),初始化并查集。并将edge按从大到小的顺序排序。(这里就是核心思想了)
- 找当前节点最小的边,
这里从大到小进行排序了,所以只用从下班最小的节点开始遍历就行。
若当前最小边的端点已经不在主节点集合当中,则加入节点集合中。
若当前最小边的端点已经在主节点集合并查集当中,则不进行加入。
- 重复2步,直到所有节点都被加入主节点并查中。
例子:
这里可以看出,最小的值是 0-》2这个路径,节点为1,则从这个边开始。
0 1 6
0 2 1
0 3 5
1 2 5
1 4 3
2 3 6
2 4 6
2 5 4
3 5 2
4 5 6
第二步:第二小的节点是3-》5,dis为2,所以将其形成又一个集合。
第四步:最小的是2-》5,距离为4
这一步发现2与五都找过了,但是都是在不同的并查集中,所以将其加入到集合中(这一步才真正显示出并查集的魅力),要比较着这个代码看更清晰。For循环那一步会寻找所以b的并查集的部分,将并查集b中的所有元素都加入到a的并查集。
接下来就一样了。
最后的图是这样的。
可能新手在这看到很奇怪,怎么不想一个路径。
因为路径我们都是从小到大排出来的,这个并查集仅仅用与查询是否加入了主节点当中。
结果:
三、代码:
#include
#include
using namespace std;
int father[6];
typedef struct {
int a;
int b;
int length;
}edge;
bool compareLength(edge a,edge b){
return a.length>edges[i].a;
cin>>edges[i].b;
cin>>edges[i].length;
}
for(int i=0;i<6;i++){
father[i]=i;//并查集
}
sort(edges,edges+10,compareLength);
printf("\n留下的边有:\n");
for(int i=0;checkFather()&&i<10;i++){//若所有节点的父节点都不为初始节点且i<10
if(father[edges[i].a]==father[edges[i].b]) continue;
else{
int num=father[edges[i].b];
for(int j=0;j<6;j++){
if(father[j]==num)
father[j]=father[edges[i].a];
}
printf("%d-%d,dis=%d\n",edges[i].a,edges[i].b,edges[i].length);
}
}
return 0;
}
总结
我在读算法的时候,发现各位博主写文章有个通病,就是不喜欢举例子,这样不利于学习,看了跟没看似的。所以我以后的文章都会举例子带大家分析,便于自学。