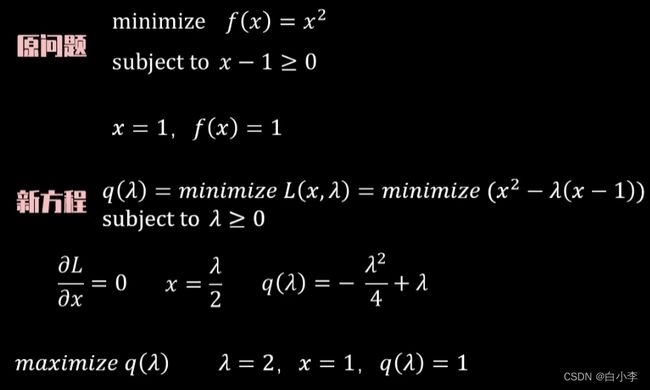2022/12/18周报

目录

摘要

文献阅读

1、题目和摘要

2、现有方法问题

3、数据处理

3、SVM模块

4、改进SVM冲突探测

5、实验结果

深度学习

1、支持向量机SVM

2、求解SVM决策超平面

3、代码

总结

---

摘要

本周在论文阅方面，阅读了一篇基于 SVM 的低空飞行冲突探测改进模型的论文，开始对SVM分类方法进行学习，在SVM的基础上，对其进行改进，在低空飞行冲突探测中能得到更好的效果。在深度学习上，了解SVM的基本特点，以及如何进行求解超平面，并进行了代码复现。

This week,in terms of thesis reading，an improved model of low altitude flight conflict detection based on SVM is read.Start learning the SVM classification method.On the basis of SVM, it is improved to get better effect in low altitude flight conflict detection.In depth learning,understand the basic characteristics of SVM and how to solve hyperplane as well as reproduce the code.

文献阅读

1、题目和摘要

基于 SVM 的低空飞行冲突探测改进模型

摘要： 为保障通航飞行器在低空空域的飞行安全,提出了一种基于支持向量机(SVM)的飞行冲突探测改进模型。 首先,建立适应于飞行器的保护区。 然后,利用改进型 ID3决策树算法将搜索空间降低到局部的方法筛选具有潜在飞行冲突的飞行器,并利用随机森林(RF)选择合适训练集。 最后,利用 tanh 函数优化容易饱和的 sigmoid 函数对 SVM 分类结果的概率映射。 通过仿真验证和对比分析,结果表明:利用基于密度聚类的 DBSACN 算法去除异常点,将剔除产生误报和虚报的数据作为训练集优化 SVM 分类器,改进的飞行冲突探测模型的误报率和虚报率分别降低了 0.6%和 1.9% ,算法执行效率得到提高,而且具有较好的抗干扰能力与稳定性。

2、现有方法问题

（1）、当将冲突的概率转化为对应于某一时刻的冲突区域与联合航迹误差的交叉体积的积分,但没有确定冲突类型。

（2）、当对冲突类型进行了数学描述,给出了确定冲突类型的方法。 但是,受到天气、环境、人为操作的误差等因素的影响,飞行器之间不是严格的几何关系,计算结果有较大误差。

（3）、概率法主要使用概率流理论、马尔可夫链、博弈论、复杂网络等方法该类方法的准确度依赖于阈值与参数的选择,较为复杂。

（4）、运用几何法研制的第二代交通防撞系统(TCAS Ⅱ)能对装有该系统的飞机发送警告,不适用于未加装该系统的通航飞行器。

（5）、采用粒子群与支持向量机( SVM) 算法得到飞行冲突概率模型,但计算复杂。

3、数据处理

离群点是指在导航设备接收到的数据中,不符合数据一般特性或者运动模型的数据。 采用DB-SCAN高分辨率的聚类算法,去除飞行数据中的离群点。

由于存在系统误差及无法消除误差的情况,飞行器的探测容易受到外界因素的干扰。 故采用以飞行器为中心建立椭球体保护区。 目标飞行器为有保护区的飞行器。椭球体的保护区用公式:

 ( x1 ,y1 ,z1 ) 表示飞行冲突的飞行器坐标;(xo,yo,zo) 为椭圆中心飞行器的位置;n、m、k 分别表示 x、y、z 三个半轴的焦距。保护区模型：

3、SVM模块

SVM 是按监督学习方式对数据进行二元分类的广义线性分类器,其决策边界是对学习样本求解的最大边距超平面。 核函数将飞行数据映射到高维空间中进行分类。

飞行数据的特征维度较低、样本中的标签较少、样本数量较多的情况下,高斯径向基核函数的分类效果较好,分类界限更准确,因此高斯径向基核函数的拟合度较好。 故在此分类中,采用 RBF。 RBF 函数作核函数。

 

σ 决定数据映射到新的特征空间分布,σ 越大,支持向量越少,σ 值越小,支持向量越多。

使用决策函数 h(x)获得标准的硬输出：h(x) = sgn(wx + b)

通过决策函数,比较 h( x)值与 0 的大小,用输出值的大小判断风险的等级,常用 sigmoid 函数把 SVM 将分类结果输出映射到[0,1]区间,带有优化的 sigmoid 函数表达式为

 f 为 SVM 的输出结果;P(y = 1|f)为输出的冲突概率。

最后采用 tanh 函数优化概率输出。tanh 的输出和输入能够保持非线性单调上升和下降关系,容错性好,有界,渐近于0 和 1,符合飞行冲突探测中冲突概率变化规律。 但由于 tanh函数输出区间为[ - 1,1],由于飞行冲突概率不存在负概率,采用输出区间[0,1]的部分。

4、改进SVM冲突探测

问题： RBF函数在将飞行数据映射到高维度的空间和分类的过程中计算量大。

改进思路：在数据集中预先找到最有可能产生冲突的飞行航迹,可有效降低 RBF 函数分类过程中及飞行冲突探测过程中的复杂度。

改进的 ID3 决策树算法：

（1）、数据的归一化处理、伸缩性处理。将训练集的样本数据分为若干个子集合,每个单独的子集组成新的决策树。

（2）、选出具有全部样本X的、规律为W的子集 X1 (W 称为窗口规模,X1 称为窗口)。

（3）、当 I(X,a) = H(X) - H(X | a)最大时,选取每次测试的属性, 形成当前窗口的决策树。

（4）、将每个子集得到的分类规则组合,得到一个分类规则。

（5）、顺序扫描子集类内的所有样本数据,如果存在不符合当前分类规则的样本,则进行步骤 4,如果不存在,则算法结束。

在 SVM 算法中,当训练集较大时,训练所需的时间及空间复杂度分别为 O( n的平方) 与 O( n的立方),n为训练集的数量,因此,需要准确取训练集。 RF是一种为分类器设计的组合方法,采用 RF 为SVM 算法提供训练集的组合。

改进模型的具体步骤：

（1）、对第 i 个飞行器的 m 个航迹归一化处理后,使用 DBSCAN 算法去除离群点,得到预处理后的航迹集合。

（2）、将预处理后飞行器之间 4 个特征量D = (d,Δv,Δr,t),利用 RF 选取适合的组合作为训练集合训练 SVM 分类器。

（3）、将预处理后的样本 X,利用改进 ID3决策树算法选择具有飞行冲突的飞行器集合Vm = (Va ,Vb,…,Vx)。

（4）、重复步骤 3,直到没有新的元素出现在集合 Vm 中。

（5）、将具有飞行冲突飞行器的集合 Vm加入已经训练的 SVM 分类器,得到分类输出集合Wm = (y1 ,y2 ,…,ym )

（6）、将步骤 5 得到的集合 Wm 用 tanh 函数映射到[0,1],得到飞行冲突概率。

（7）、将得到的结果,去除产生虚报和误报的数据,组成特征量训练集,训练 SVM 分类器。

5、实验结果

一个飞行器为实际飞行器,设置一个与实际飞行器存在或不存在飞行冲突的仿真飞行器,从而实现模拟双机飞行。

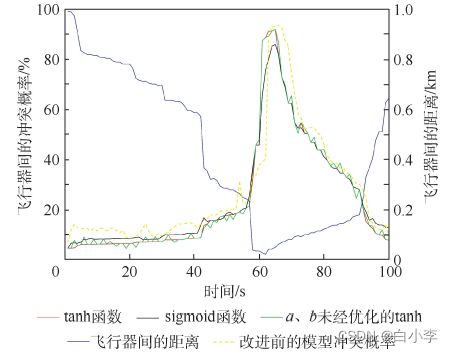
为分析 tanh 函数与 sigmoid 函数在飞行冲突探测过程对分类结果的映射效果,将水平方向上的飞行冲突分类结果用 sigmoid 函数和 tanh 函数进行映射,比较如下：

 

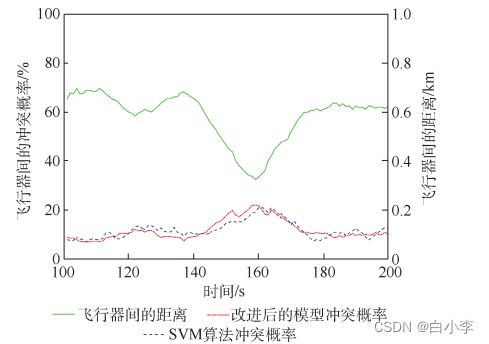
高度冲突验证与分析：在 108 ~ 118 s与 140 s ~ 159 s 内,改进后的探测模型得到的飞行冲突概率变化曲线更稳定。 SVM 算法在 t = 160 s 时刻给出最大冲突概率,该探测模型的性能更好。

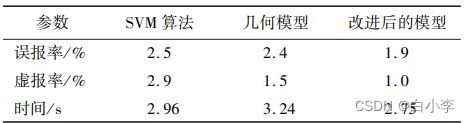
 将具有飞行冲突的飞行器作为研究对象,利用飞行器的飞行数据来验证算法的准确度与复杂度,其中算法时间、误报率与虚报率取 300 次模拟运行结果的平均值。

 可以看出,在相同条件下,相较于其他2 种方法,改进后的探测模型降低了飞行冲突探测误报率与虚报率,所运行的时间分别减少了0.21 s与 0.49 s。

改进总结：

（1）、采用椭球体保护区,降低了数据的误差对冲突过程中的干扰,采用 DBSCAN 聚类算法、优化训练集的方法减小了 SVM 算法的误差。

（2）、利用 RF、决策树、降低数据维度的方法,减小了 SVM 算法的复杂度。

（3）、相较于 SVM 算法,改进后的模型的误报率与虚报率较低,算法运行时间较少,而且具有较好的抗干扰能力和稳定性。

深度学习

1、支持向量机SVM

含义：一类按监督学习方式对数据进行二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面，可以将问题化为一个求解凸二次规划的问题。

优点：a、SVM是一种有坚实理论基础的传统机器学习方法。它基本上不涉及概率测度及大数定律等，也对通常的回归与分类问题做了简化。

b、由于使用了核函数，使得其计算的复杂性取决于支持向量的数目，而不是样本空间的维数，这在某种意义上避免了“维数灾难”。

c、支持向量机算法利用松弛变量可以允许一些点到分类平面的距离不满足原先要求，从而避免这些点对于模型学习的影响。

缺点：a、难以训练大规模数据集

b、需要组合多个二分类SVM来实现多分类

c、对参数和核函数选择敏感

为了区分两类维度数据，N为数据的样本数，，M为维度数，如何设计一个为M-1的超平面，将两类数据区分开了。

SVM的本质是求解三个超平面方程（以二维数据举例）:正超平面、负超平面、决策超平面。当有新数据进来的时候，利用决策超平面来对它进行分类。

 损失因子：违背规则的异常点都会有对应的损失值

升维：通过合适的维度转换函数，将低维数据进行升维，在高维数据下求解SVM模型，找到对应的分隔超平面。

核技巧（Kerner Trick）能够提供高纬度向量相似度的测量，通过选取合适的核公式，从而不用知晓具体的维度转换函数，直接获得数据的高纬度差异度。

2、求解SVM决策超平面

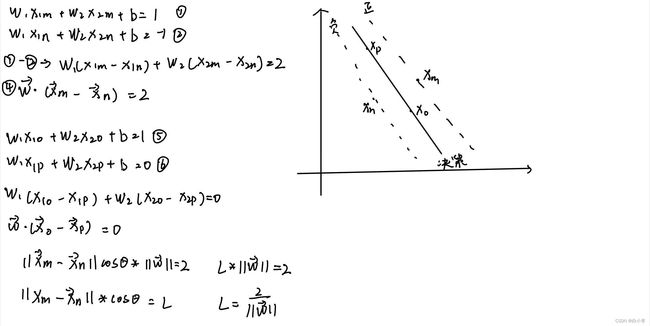
随机在正负超平面上选取一个支持向量点xm和xn,在决策超平面上随机选取2个点p ,o，求间隔L。

 接下来是对向量w求最小。问题转变为：

 

通过拉格朗日法求解最小值：

 将λi作为惩罚因子，λi>=0。

SVM对偶性，求解原问题的对偶问题来解决原问题。（举例）

 转化为原问题求解超平面的思路

 

3、代码

对线性可分的数据求解SVM支持向量点和分类器

from time import sleep
import matplotlib.pyplot as plt
import numpy as np
import random
import types
​
#函数说明:读取数据
def loadDataSet(fileName):
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():                                     #逐行读取，滤除空格等
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]), float(lineArr[1])])      #添加数据
        labelMat.append(float(lineArr[2]))                          #添加标签
    return dataMat,labelMat
​
#函数说明:随机选择alpha
def selectJrand(i, m):
    j = i                                 #选择一个不等于i的j
    while (j == i):
        j = int(random.uniform(0, m))
    return j
​
#函数说明:修剪alpha
def clipAlpha(aj,H,L):
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj
​
#函数说明:简化版SMO算法
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
    #转换为numpy的mat存储
    dataMatrix = np.mat(dataMatIn); labelMat = np.mat(classLabels).transpose()
    #初始化b参数，统计dataMatrix的维度
    b = 0; m,n = np.shape(dataMatrix)
    #初始化alpha参数，设为0
    alphas = np.mat(np.zeros((m,1)))
    #初始化迭代次数
    iter_num = 0
    #最多迭代matIter次
    while (iter_num < maxIter):
        alphaPairsChanged = 0
        for i in range(m):
            #步骤1：计算误差Ei
            fXi = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
            Ei = fXi - float(labelMat[i])
            #优化alpha，更设定一定的容错率。
            if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
                #随机选择另一个与alpha_i成对优化的alpha_j
                j = selectJrand(i,m)
                #步骤1：计算误差Ej
                fXj = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
                Ej = fXj - float(labelMat[j])
                #保存更新前的aplpha值，使用深拷贝
                alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy();
                #步骤2：计算上下界L和H
                if (labelMat[i] != labelMat[j]):
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if L==H: print("L==H"); continue
                #步骤3：计算eta
                eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
                if eta >= 0: print("eta>=0"); continue
                #步骤4：更新alpha_j
                alphas[j] -= labelMat[j]*(Ei - Ej)/eta
                #步骤5：修剪alpha_j
                alphas[j] = clipAlpha(alphas[j],H,L)
                if (abs(alphas[j] - alphaJold) < 0.00001): print("alpha_j变化太小"); continue
                #步骤6：更新alpha_i
                alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])
                #步骤7：更新b_1和b_2
                b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
                b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
                #步骤8：根据b_1和b_2更新b
                if (0 < alphas[i]) and (C > alphas[i]): b = b1
                elif (0 < alphas[j]) and (C > alphas[j]): b = b2
                else: b = (b1 + b2)/2.0
                #统计优化次数
                alphaPairsChanged += 1
                #打印统计信息
                print("第%d次迭代 样本:%d, alpha优化次数:%d" % (iter_num,i,alphaPairsChanged))
        #更新迭代次数
        if (alphaPairsChanged == 0): iter_num += 1
        else: iter_num = 0
        print("迭代次数: %d" % iter_num)
    return b,alphas
​
#函数说明:分类结果可视化
def showClassifer(dataMat, w, b):
    #绘制样本点
    data_plus = []                                  #正样本
    data_minus = []                                 #负样本
    for i in range(len(dataMat)):
        if labelMat[i] > 0:
            data_plus.append(dataMat[i])
        else:
            data_minus.append(dataMat[i])
    data_plus_np = np.array(data_plus)              #转换为numpy矩阵
    data_minus_np = np.array(data_minus)            #转换为numpy矩阵
    plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1], s=30, alpha=0.7)   #正样本散点图
    plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1], s=30, alpha=0.7) #负样本散点图
    #绘制直线
    x1 = max(dataMat)[0]
    x2 = min(dataMat)[0]
    a1, a2 = w
    b = float(b)
    a1 = float(a1[0])
    a2 = float(a2[0])
    y1, y2 = (-b- a1*x1)/a2, (-b - a1*x2)/a2
    plt.plot([x1, x2], [y1, y2])
    #找出支持向量点
    for i, alpha in enumerate(alphas):
        if alpha > 0:
            x, y = dataMat[i]
            plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
    plt.show()
​
#函数说明:计算w
def get_w(dataMat, labelMat, alphas):
    alphas, dataMat, labelMat = np.array(alphas), np.array(dataMat), np.array(labelMat)
    w = np.dot((np.tile(labelMat.reshape(1, -1).T, (1, 2)) * dataMat).T, alphas)
    return w.tolist()
​
​
if __name__ == '__main__':
    dataMat, labelMat = loadDataSet('testSet.txt')
    b,alphas = smoSimple(dataMat, labelMat, 0.6, 0.001, 40)
    w = get_w(dataMat, labelMat, alphas)
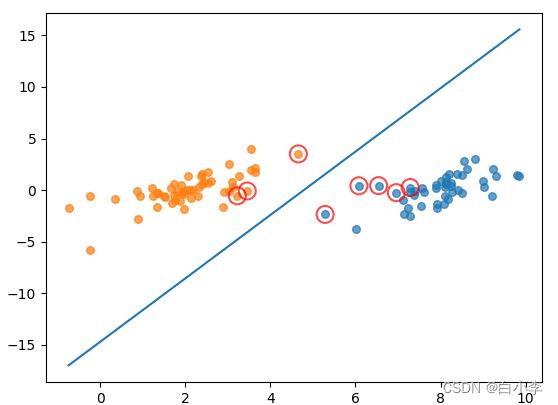
    showClassifer(dataMat, w, b)

中间的蓝线为求出来的分类器，用红圈圈出的点为支持向量点。

总结

这次是对SVM进行了初步的学习，刚开始接触，只是学了个大概，下周从SVM的核函数部分开始学习，将SVM应用于非线性数据集。