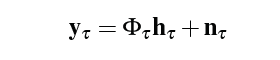信道估计（二）：卡尔曼滤波器
信道估计（二）：卡尔曼滤波器
零.概述
卡尔曼滤波器可以说是大名鼎鼎了，在我本科期间就在惯性传感器的使用上听过，但一直不知道是什么，刚好通过这篇论文学习一下
论文是这样描述他的，使用先验的状态空间模型和状态向量的估计，估计出后验的信道估计。
一.什么是卡尔曼滤波器？
卡尔曼滤波器是通过观测值和上一时刻的最优预测值来预测下一时刻的最优预测值的算法
https://www.bilibili.com/video/BV1Rh41117MT?spm_id_from=333.337.search-card.all.click
这个视频讲的是很明白的，建议大家看完这个视频，再来看我接下来的论述
在信道预测中，是没有输入的，信道的变化实际上是由于环境的变换引起的，这可以看作噪声就是输入，因此在此预测中，状态空间方程是这样的：
他也代表了先验估计。
我们解释一下里面的每一个参数
w r w_r wr是一个噪声，他的自相关函数是Q。
x r x_r xr是被用于估计的向量，它是用来估计h的
A B C ABC ABC是状态空间方程的参数
n A R n_{AR} nAR是卡尔曼滤波器的增益
下面看一下观测方程
这就是之前所述的导频方程，而他存在一个观测误差，其自相关矩阵一般表示为R
下面定义一个很重要的矩阵P，它代表的是估计误差的协方差矩阵
有了观测方程，状态空间方程，还有估计误差的协方差矩阵，我么就可以进行卡尔曼滤波了
二.如何使用卡尔曼滤波器实现预测或是平滑？
上面说的，其实都是滤波的事情，那如何实现预测呢？
实际上，这就是说没有观测值的情况下如何继续进行？只要自然的往下算，预测出的最有估计值占100%的权重就可以了，也就是卡尔曼增益为0
显然预测的效果是不如卡尔曼滤波好的
三. 卡尔曼滤波的稳态
什么时候卡尔曼滤波达到稳态呢？协方差矩阵不再更新变化的时候
此时P是可解的
四. 如何获得状态空间方程？
卡尔曼滤波器必须要有先验估计，这个先验估计如何获得呢？是通过Yule-Walker方程求解得到的
AR模型使用来描述时间序列的，对于信道里的每一个元素，都可以看做一个时间序列，就可以用AR模型来进行建模，计算出他的自相关矩阵，然后计算Yule-Walker方程方程，在计算每一个元素，进而就可以获得先验估计
五. Q的估计
在卡尔曼滤波中，Q和R是非常重要的超参数，书中给出了一个卡尔曼滤波Q的估计方法，他表示了信道每一个元素之间的相关性，可以用于MIMO信道中，因为他们是同分布的
六. 现实中的AR模型
Walker方程并不好求解，加上一个小正数会容易，而这个小正数在现实中往往是存在的吗，由于各种噪声干扰，因此在模型中我们也会把它加上
七.R的估计
有Jakes模型，这里的R不是卡尔莫纳滤波器中的R，而是信道的自相关函数
八.卡尔曼滤波器的完整预测过程
解Walker方程得到AR模型，然后计算导频， 然后用后验方程预测
九. 卡尔曼滤波器的预测影响因素
- 影响最大的是训练数据的数量和质量
- 第二个是 n A R n_{AR} nAR但不是越大越好，在数据不够的时候，反而缔结的表现更好
- 测量噪声
十.预测器位置的放置
预测器可以选择放在用户端或者是基站端
基站端的好处是
- 基站端的运算能力更强，可以使用更高阶的算法
- 可以调整预测范围
用户端的好处是
- 可以灵活的选择量化精度
- 降低反馈开销
十一. 导频设计
这里没怎么看懂。。。。看懂了在更新