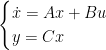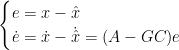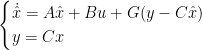状态观测控制器设计与仿真验证
【无限嚣张(菜菜)】:hello您好,我是菜菜,很高兴您能来访我的博客,我是一名爱好编程学习研究的菜菜,每天分享自己的学习,想法,博客来源与自己的学习项目以及编程中遇到问题的总结。
座右铭:尽人事,听天命
个人主页:无限嚣张(菜菜)
目录
- 状态观测器的提出
- 状态观测器定义
- 状态观测器的设计原理
- 状态观测器的设计
- 状态观测器的仿真验证
状态观测器的提出
并不是所有系统的状态变量都是很容易能直接检测得到的,大多系统的状态变量都是不容易直接检测到的,有些状态变量甚至根本无法检测。这样,就提出了所谓的状态观测和状态重构问题,由龙伯格(Luenberger)提出的状态观测器理论,所以也叫Luenberger观测器。通过系统的输入和输出来估计状态,从而解决了在确定性条件下受控系统的重构问题,从而使状态反馈成为一种可实现的控制率。
状态观测器定义
设线性定常系统![]() 的状态矢量x不能直接检测。如果动态系统
的状态矢量x不能直接检测。如果动态系统![]() 以
以![]() 的输入u和输出y作为其输入量,能产生一组输出量
的输入u和输出y作为其输入量,能产生一组输出量![]() 渐近于x,即
渐近于x,即![]() ,则称
,则称![]() 为
为![]() 的一个状态观测器。
的一个状态观测器。
根据状态观测器的的定义,我们可以知道构造观测器的原则是:
(1)观测器![]() 应以观测器
应以观测器![]() 的输入u和输出y作为输入量。
的输入u和输出y作为输入量。
(2)为了满足![]() ,
,![]() 必须完全能观,或其不能观子系统是渐进稳定的。
必须完全能观,或其不能观子系统是渐进稳定的。
(3)![]() 的输出
的输出![]() 应以足够的速度渐进与x,即
应以足够的速度渐进与x,即![]() 应有足够宽的频带。但从抑制干扰角度看,又希望频带不要太宽。因此,要根据具体情况予以兼顾。
应有足够宽的频带。但从抑制干扰角度看,又希望频带不要太宽。因此,要根据具体情况予以兼顾。
(4)![]() 在结构上要尽量简单。即具有尽可能低的维数,以便于物理实现。
在结构上要尽量简单。即具有尽可能低的维数,以便于物理实现。
状态观测器的设计原理
给出单输入单输出系统如下,假设给出的系统是能观(![]() )的,如果不能观,我们设计降阶观测器,观测他一部分状态。
)的,如果不能观,我们设计降阶观测器,观测他一部分状态。
根据观测器的设计原则,闭环观测器的的状态方程设计如下:
![]()
我们可以很容易知道闭环观测器的误差状态
证明确定使![]() 渐进与x的条件:
渐进与x的条件:
对误差求导,我们可以得到如下解:
![]()
由上式可知,当(A-GC)的特征值均为负实部,才能满足![]()
状态观测器的设计
假设一个线性系统如下:
将上式写成状态空间的形式如下,设![]()
判断系统是否能观:![]() ,由此可知,此系统是满秩,所以能观,根据状态观测器的构造原则可知,可以构造观测器。
,由此可知,此系统是满秩,所以能观,根据状态观测器的构造原则可知,可以构造观测器。
原系统构建:若原系统渐进稳定,那么矩阵A满足Hurwitz条件,即系统A的所有特征值全部小于0.即
![]()
因此特征值和积需满足:![]() ,取
,取![]()
观测器构建:
观测器的误差为:
我们最初目的是为了让![]() ,也就是目的让误差趋于0。此时我们需要让矩阵A-GC满足Hurwitz条件,即:
,也就是目的让误差趋于0。此时我们需要让矩阵A-GC满足Hurwitz条件,即:
将![]() 带入上式中,我们并求det(
带入上式中,我们并求det(![]() I-(A-GC)),使其满足Hurwitz条件
I-(A-GC)),使其满足Hurwitz条件
det(![]() I-(A-GC))=
I-(A-GC))=![]() ,
,
因此特征值和积需满足,![]() ,取
,取![]()
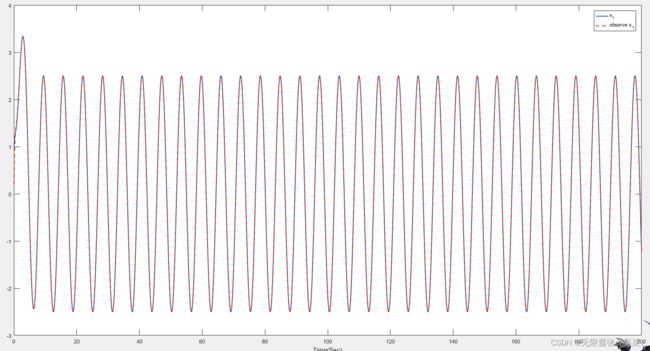
状态观测器的仿真验证
控制输入,也就是控制器,我们输入一个正弦函数
x1的状态,以及x1的状态观测
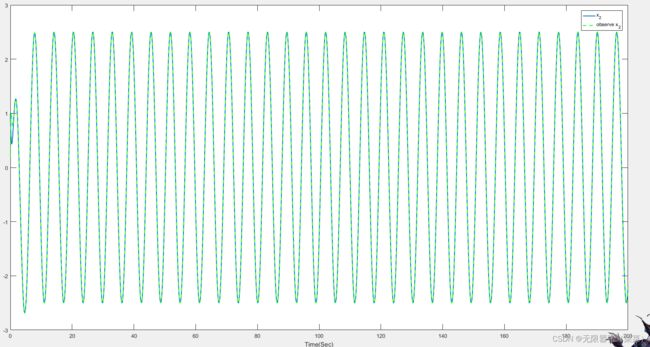
x2的状态,以及x2的状态观测
代码:
clc
clear all
close all
stepLength = 0.002;
N = 100000;
timeStart = 0;
timeEnd = N * stepLength;
t = timeStart:stepLength:timeEnd ;
u = sin(t);
k = 1; % 迭代起始步数
x1 = zeros(size(t));
x2 = zeros(size(t));
x1(:,1) = 1;
x2(:,1) = 1;
x1_hat = zeros(size(t));
x2_hat = zeros(size(t));
x1_hat(:,1) = 0.2;
x2_hat(:,1) = 0.2;
for tt = timeStart : stepLength: (N-1)*stepLength
k
% 原系统
dx1 = x2(:,k);
dx2 = -x1(:,k)-2*x2(:,k)+5*u(:,k);
% 观测器
dx1_hat = x2_hat(:,k)+5*(x1(:,k)-x1_hat(:,k));
dx2_hat = -x1_hat(:,k)-2*x2_hat(:,k)+5*u(:,k)+2*5*(x1(:,k)-x1_hat(:,k));
%
% 更新坐标
x1(:,k+1) = x1(:,k) + dx1 * stepLength;
x2(:,k+1) = x2(:,k) + dx2 * stepLength;
x1_hat(:,k+1) = x1_hat(:,k) + dx1_hat * stepLength;
x2_hat(:,k+1) = x2_hat(:,k) + dx2_hat * stepLength;
k = k+1;
end
figure
plot(t,x1,'linewidth',1.5)
hold on
plot(t,x1_hat,'--red','linewidth',1.5)
hold on
xlabel('Time(Sec)')
legend('x_{1}','observe x_{1}')
figure
plot(t,x2,'linewidth',1.5)
hold on
plot(t,x2_hat,'--green','linewidth',1.5)
hold on
xlabel('Time(Sec)')
legend('x_{2}','observe x_{2}')