无线信道

文章目录

前言

一、坐标系转换

1.笛卡尔坐标系

2.极坐标系

二、极化场分量

1.一般场景

2.下倾角场景

二、天线阵列建模

三、快速衰落信号

1.CDL-C信道

2.信道系数计算

总结

---

前言

本文 主要介绍一下5G物理层信道相关的内容，以协议38.901为基础，讨论信道建模相关的问题。

 

一、坐标系转换

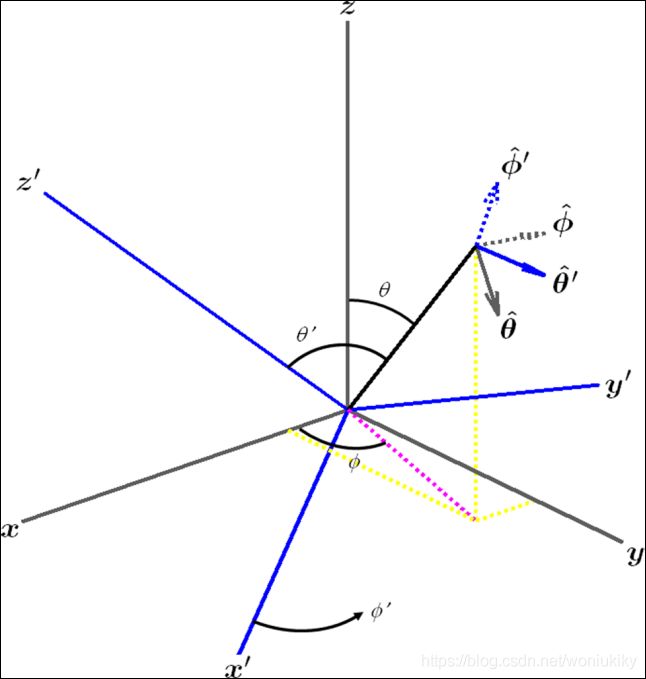
                                                 Fig1. GCS坐标示意图 

    全局坐标系统（GCS）是为系统中存在多个基站和用户终端的场景定义的。单个基站或者终端的天线阵列可以定义在局部坐标系（LCS）中。天线阵列矢量是定义在LCS上的，而LCS与GCS之间的转换取决于角度，其中称为象限角（z轴固定，x轴转动的角度），称为下倾角（y轴固定，z轴转动的角度），称为倾斜角（x轴固定，y轴转动的角度）。转动的时候是先固定z轴，然后固定y轴，然后固定x轴。

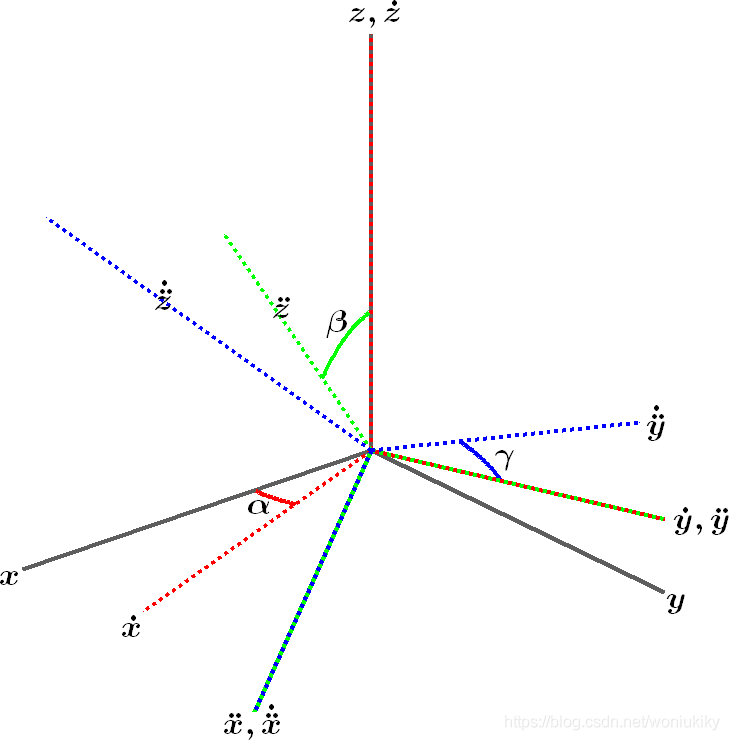
                                                                                                Fig2. GCS到LCS坐标旋转示意图

上图中灰色线条坐标表示GCS的位置，而蓝色线条坐标表示LCS的位置。

1.笛卡尔坐标系

由GCS到LCS的旋转，使用矩阵表示定义如下：

以上式子有个特点，矩阵中角度是相对于哪个轴的，哪个轴对应的正余弦符号都是正的，并且在该轴对应行列的交点处的系数是求角度的余弦。另外一个随动轴上系数，余弦是正号，正弦是负号，也是在随动轴对应行列的交点处求角度的余弦。以下以z轴不动x轴转动角度为例做说明。如下图：

Fig3. GCS到LCS旋转矩阵规律示意图

上图中黑线圈出的部分对应x轴对应的行和列，橙色圈出的部分为随动轴y轴对应的行和列，而z轴不同，所以矩阵中只在交点出为1，其他位置为0。

由于R矩阵是正交矩阵，R的逆等于R矩阵的转置。矩阵展开写，得到R矩阵的公式如下：

注意，R矩阵是从GCS到LCS的转换矩阵，若需要从LCS转换到GCS，则应该用R的逆矩阵。另外要右乘R，那么[x y z]应该是行向量的形式。

2.极坐标系

极坐标与笛卡尔坐标系转换服从下式：

若表示GCS的角度，那么要得到LCS对应的角度，可通过公式来计算。注意到由于这里[x y z]变成了列向量，因此转换矩阵变成了用R的转置（即R的逆）左乘。

 上式中通过与[0 0 1]的转置相乘求得LCS对应的z坐标，再求acos，即可得到角度。

 上式中通过与[1 j 0]的转置相乘求得LCS对应的x+jy坐标，再求角度，即可得到角度。

二、极化场分量

1.一般场景

GCS的极化场分量,与LCS的极化场分量,之间的关系为：

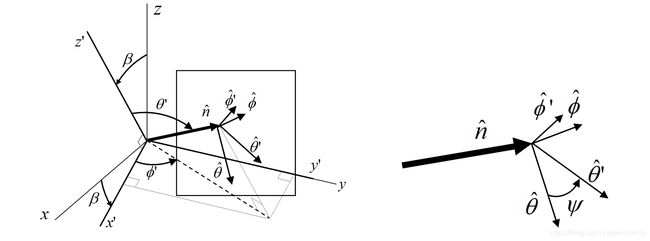
,以及,指的是波阵面的方向矢量，个人理解在该坐标下电磁场公式可较简单地表达。而上式表达了LCS下场分量与GCS下场分量的转换关系。当已知旋转角度的情况下（如下图），公式可简化。

Fig4. 场矢量GCS到LCS旋转示意图

公式简化过程如下：

 

2.下倾角场景

基站GCS的x轴对准探测器指向的方向。在只考虑下倾角的场景下，天线面板y轴与GCS的y轴重叠，沿y轴旋转角度。

                                                                                                                                                                Fig5. 只考虑下倾角时GCS到LCS旋转示意图

对于机械下倾角为时：

（1）GCS与LCS对应的极化方向关系为：

（2）GCS与LCS之前极化场分量换算关系为：

其中方向矢量旋转角度ψ计算方法如下：

从以上描述推测，信号如果是正对入射基站的话，应该跟x轴方向一致，大致坐标如下：

        Fig6. 基站与天线阵列坐标转换示意图

上图中黑色框表示基站的天线面板。绿色坐标系表示基站坐标系，这里认为是GCS坐标系。而天线面板坐标系为红色坐标系，这里认为是LCS坐标系。上图中LCS相对GCS有角度的下倾角。

二、天线阵列建模

天线阵列由个面板组成，表示面板垂直方向的行数，表示面板水平方向的列数。每个面板内部有MN个天线单元，每个天线单元极化个数为P（P=1或者2）。面板水平和垂直间距分别为和。面板内天线单元水平和垂直间距分别为和。

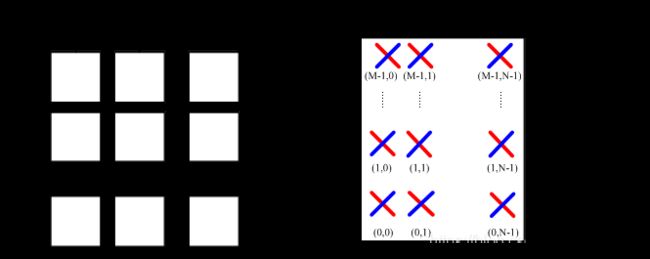
                                   Fig7.天线阵列示意图

天线阵列坐标，y轴指向列增加的方向，x轴是垂直于纸面方向的，z轴行增加的方向（上图中从0指向M-1）。

• 每个天线单元都有自己的功率分布，记为
• 对于M个天线阵列，可通过每天线固定的相移，实现波束倾斜

为垂直倾斜角度。

• 极化天线建模

天线极化场与功率分布之间的关系如下：

而极化场建模时，假设极化倾角为，那么场旋转角度为ψ，与倾角的关系类似于上节中下倾角=的情况，则有：

假设不存在极化倾斜角情况下的极化场为和，则存在极化倾角的极化场和。两者之间的关系如下式：

三、快速衰落信号

信道模型中只定义了经过最后一个散射体的到达角以及到达第一个散射体的离开角。其中AOA和AOD指的是方位角，ZOA和ZOD指的是天顶角。这些角度都定义在GCS中。

信道模型中还定义了多普勒频移的天顶角和方位角，此角度是个配置值与AOA和ZOA没有关系，不过最终基站感知到的速度还是跟AOA和ZOA有关的，当和一定的情况下，速度与AOA和ZOA角度越接近，基站感知到的速度会越大？

以上与点乘，实际上就是速度方向在射线方向的投影，若知道两个方向之间的夹角，那么之间乘以就可以得到分子相同的结果。

1.CDL-C信道

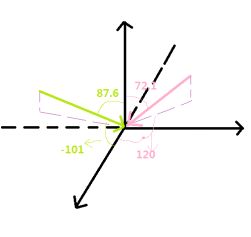
在CDL-C信道下，存在24条主径（cluster）,每条主径存在20条子径（rays），每条主径都会有个一套角度（AOA，ZOA，AOD，ZOD）。下表为CDL-C信道前两个cluster参数：

Cluster #	Normalized delay	Power in [dB]	AOD in [°]	AOA in [°]	ZOD in [°]	ZOA in [°]
1	0	-4.4	-46.6	-101	97.2	87.6
2	0.2099	-1.2	-22.8	120	98.6	72.1

这两个cluster，两条主径入射示意图如下：

Fig8.CDL-C入射角示意图

每条主径都存在20个子径，那么子径的角度分布，协议有如下定义：

其中是协议规定的角度扩展量，CDL-C规定是15度，而是具体到每个子径的角度偏移比例，如下表所定义。

Ray number m	Basis vector of offset angles am
1,2	± 0.0447
3,4	± 0.1413
5,6	± 0.2492
7,8	± 0.3715
9,10	± 0.5129
11,12	± 0.6797
13,14	± 0.8844
15,16	± 1.1481
17,18	± 1.5195
19,20	± 2.1551

基站在接收信号的时候，水平方向是360度都能接收的，一般垂直角度不会变化太大。

协议以上定义的角度是个总体分布，会以定义的总体参数AOA，AOD，ZOA，ZOD作为偏置，进行整体的旋转。

2.信道系数计算

协议中给出公式如下：

这个公式看起来很复杂，可以分开来看。相关下表含义总结如下：

参数	含义
n	主径编号
m	主径内子径编号
M	子径数
	主径n的功率
u	天线单元u
	天顶角
	方位角

1.Part1 And Part3

这两部分是收发天线的场矢量，假设接收天线极化角度为,LCS坐标系下Part1为[cos sin],在已知LCS和GCS的的情况下，可根据公式转换到GCS。对于发射天线，Part3也是类似的。

2.Part2

是极化天线四个组合下的随机初始相位，值协议中有定义。就是一个随机的初始相位。

3.Part4

这个部分是收发天线的天线特征图向量，与接收和发送径的空间角度有关。

4.Part5

这个部分体现多普勒的作用。与接收径与速度方向有关。速度的方向定义为和，这个角度定义的是与基站GCS坐标之间的夹角，基站看到的速度是，假设接收径与速度方向的夹角为,那么基站感应到的速度是。.

---

总结

本文详细讨论了38.901协议中信道相关的关键问题。总的来说，协议里面定义的各种参数和角度都是基于LCS的，但基站信道建模需要基于GCS，因此各UE在按照协议的参数进行建模，之后再转到GCS坐标系中模拟多天线，极化以及速度的场景。

备注：对本文中的内容有任何问题，欢迎发送邮件至[email protected]，很高兴进行相关交流。