学习自旋电子学的笔记03:初试自旋波模拟
文章目录
- 前言
- 一、初遇
-
- 1.Figure S2 (a)
- 2.图4-2
- 3.Figure S1
- 二、暂别
-
- 1.FFT分析程序包:MFA简介
- 2.使用练习MFA
- 三、重逢
-
- 3.Figure S1
- 4.FIG.2 (a)
- 5.FIG.2 (b)
- 6.FIG.5
- 总结
_ _ 远行!
前言
四月,过得四真的快啊,这是从入学到现在的第9个月了。现在的我年纪轻轻一个月就能看了3200e-3篇文章,是3200e-3篇哦,你们敢想吗,不是偷懒啊,我是真的看得脑壳痛啊,毕竟人和人之间是不同的,有人天生就聪明,有人天生就笨。这3.2篇文章都是关于自旋波的。到了现阶段,相信大部分同学都已经复现过别人文章里的模拟了,或者厉害的大佬已经开始写文章了,所以作为咸鱼的我也正在复现本人觉得自己有能力复现的一篇文章。不过,截止此刻,我也还是没有完全能复现出来,本着不能在一颗树上吊死的原则,所以就不再继续模拟这篇文章了。一、初遇
事情的起因是这样的,刚开始时读到一篇硕士论文《光纤型磁振子波导中自旋波的电流操纵》,它里面介绍的小论文是这一篇:DOI:10.1063/5.0034837,此外这小论文还有一篇补充材料。关于这篇文章,若感兴趣的同学可以康康,试一试把它复现出来,然后可以教一教我。。。这篇文章的主要意思是:在FM/HM双层磁体系中,通过HM层电流产生的SOT作用在FM层,在FM层中的neel畴壁传播的自旋波会被调制,在模拟时,把HM层对FM层的影响等效为FM层的磁性参数,所以无需分别建立两层体系,模拟得到的结论大致就是:在合适大小的电流密度范围内,正的电流密度会对在neel畴壁中传播的自旋波有放大作用,负的电流密度会对在neel畴壁中传播的自旋波有衰减作用。
硕士论文在第四章中给出了磁体系的模型和参数:纳米带尺寸为 2000nmX60nmX1nm,网格尺寸为1nmX1nmX1nm,能量项有:交换能(A=15pJ/m),退磁能,等效的单轴各向异性能(Ku=0.8MJ/m3),塞曼能,界面DMI能(D=3.5mJ/m2)。饱和磁化强度Ms=580kA/m,自旋霍尔角=0.13,阻尼系数按区域分布。具体模拟细节请参考原文!
我之所以觉得自己能复现出来,是因为这篇文章的附录有模拟代码,所以只需修改部分参数进行模拟,对模拟得到的数据进行处理就可以复现出来,,,吧。

文章中的图片也不算多,这里只选取部分看起来比较简单的图片进行复现:

那么以上6张图分别就对应6个模拟仿真:
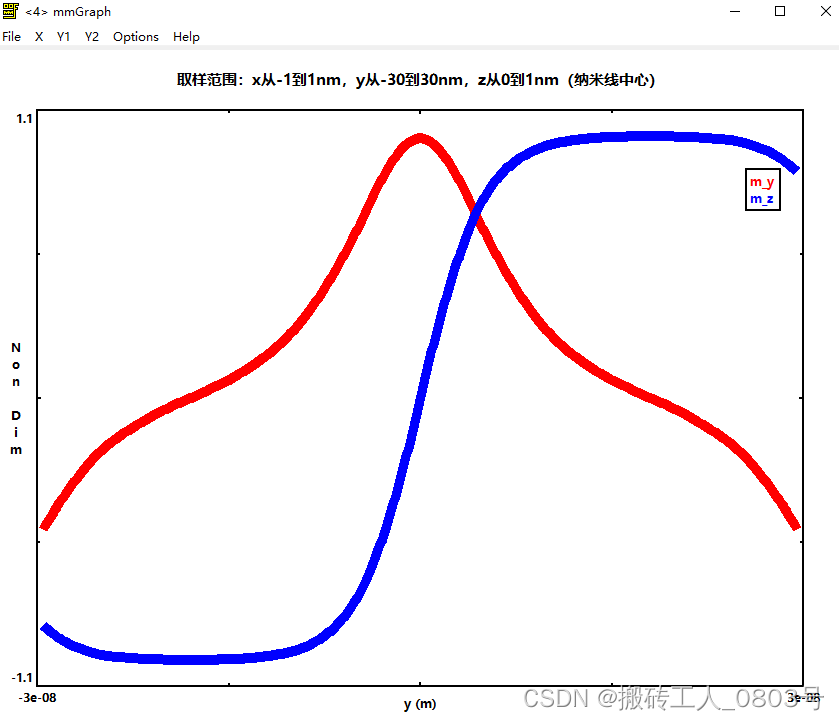
1.Figure S2 (a):磁体系弛豫到稳态后,提取neel畴壁中y和z方向的磁化分量。
2.图4-2:没有激发自旋波时,测试磁体系在不同电流密度作用下,能保持稳定,neel畴壁不变形的临界电流密度。
3.Figure S1:电流密度J0为1e10A/m2时,测试在SOT作用的类场项系数bJ和类阻尼项系数aJ的不同比值影响下,对激发的自旋波进行FFT分析。
4.FIG.2 (a):当忽略SOT的类场项作用时,测试在不同电流密度作用下时,对激发的自旋波进行FFT分析。
5.FIG.2 (b):当忽略SOT的类场项作用时,测试不同频率的自旋波在不同电流密度下的衰减长度。
6.FIG.5:当忽略SOT的类场项作用时,在不同电流密度作用下,对激发的自旋波进行色散分析。
1.Figure S2 (a)
磁体系弛豫到稳态后,提取neel畴壁中y和z方向的磁化分量。这是最容易实现的模拟,首先,将纳米条的上下部分的初始磁化设置为垂直方向相反,上下相邻区域的初始磁化设置为y方向,在界面DMI作用下,使用能量最小化演化器一直模拟到求解器自动停止即可,弛豫之后会得到稳定的neel畴壁。模拟使用的代码如下:
# MIF 2.1
#################
#author:YQYUN
#date:22/4/8
#desc:电流控制纳米线中,neel磁畴壁波导中的自旋波(振幅放大或缩小)
#desc:该文件是用于将纳米线弛豫并得到稳态neel畴壁
#################
set pi [expr {4*atan(1.0)}]
set mu0 [expr {4*$pi*1e-7}]
#纳米线尺寸:2000*60*1nm
Parameter nanowire_x 2000
Parameter nanowire_y 60
Parameter nanowire_z 1
set nanowire_x [expr {$nanowire_x*1e-9}]
set nanowire_y [expr {$nanowire_y*1e-9}]
set nanowire_z [expr {$nanowire_z*1e-9}]
#单元格尺寸:1*1*1nm(单元格尺寸小于交换长度Lex=8.4nm)
Parameter xcell 1
Parameter ycell 1
Parameter zcell 1
set xcell [expr {$xcell*1e-9}]
set ycell [expr {$ycell*1e-9}]
set zcell [expr {$zcell*1e-9}]
#定义纳米线形状,按照DMI示例文件中的形式,需要使用Oxs_MultiAtlas
Specify Oxs_MultiAtlas:atlas [subst {
atlas { Oxs_BoxAtlas:world {
xrange {0 $nanowire_x}
yrange {0 $nanowire_y}
zrange {0 $nanowire_z}
name world
}}
}]
#定义网格尺寸
Specify Oxs_RectangularMesh:mesh [subst {
cellsize {$xcell $ycell $zcell}
atlas :atlas
}]
#定义交换能(15pJ/m)
Specify Oxs_UniformExchange {
A 15e-12
}
#定义单轴各向异性能(0.8MJ/m3)
Specify Oxs_UniaxialAnisotropy {
K1 0.8e6
axis {0 0 1}
}
#定义退磁能
Specify Oxs_Demag {}
#定义DMI能(3.5mJ/m2)
set D 3.5
set DD [expr {$D/1000}]
Specify Oxs_DMExchange6Ngbr:DMEx [subst {
default_D $DD
atlas :atlas
D {
world world $DD
}
}]
#定义饱和磁化强度Ms(5.8e5A/m)
set Ms 5.8e5
###########得到位于纳米线中心,沿着x方向的neel畴壁###########
# 先使用能量最小化演化器弛豫到neel畴壁,作为初始态并保存
# 文件名“stable_neel_domain_wall.omf”
Specify Oxs_CGEvolve:evolver {}
#在纳米线y方向的中心位置,畴壁厚度sqrt(A/Ku)=4nm,设置畴壁的方向,畴壁两侧磁化方向设为垂直方向且相反
proc setNeelWall { x y z } {
global nanowire_y
#畴壁下方的磁化方向设为垂直向下
if {$y <= $nanowire_y / 2 - 2e-9} {
return "0 0 -1"
}
#畴壁上方的磁化方向设为垂直向上
if {$y >= $nanowire_y / 2 + 2e-9} {
return "0 0 1"
}
#畴壁的磁化方向设为+y方向
return "0 1 0"
}
#使用最小化驱动器快速推进到稳态
Specify Oxs_MinDriver [subst {
evolver :evolver
mesh :mesh
stopping_mxHxm 0.1
comment "饱和磁化强度为5.8e5A/m"
Ms $Ms
m0 { Oxs_ScriptVectorField {
atlas :atlas
norm 1
script setNeelWall
script_args rawpt
}
}
}]
###########得到位于纳米线中心,沿着x方向的neel畴壁###########
模拟结束后,即弛豫后得到的稳态磁化分布如图:
接着需要将这个磁化文件保存,可以在代码末尾添加保存语句实现自动保存,也可以在3D求解器Oxsii中选择手动保存,文件名为“stable_neel_domain_wall.omf”,将它作为后面一系列模拟的初始磁化状态。接着需要提取畴壁中磁化强度的y和z分量,利用oommf自带的命令行工具avf2odt即可提取,但是文中并没有明确说明提取磁化强度的空间范围,所以在这里,把提取的范围设置为纳米线中心区域2nmX60nmX1nm的空间范围,但直接按照这个参数来提取的话,得不到Figure S2 (a)的效果,仔细观察图中y的范围是-30nm到30nm,结合毕业论文附录的代码,说明它是在模拟结束得到稳态畴壁后,将这个磁体系的坐标原点从左下角移动到了纳米线的中心。那么,磁体系的坐标系变换见后文的代码注释,将坐标系平移之后,再次保存当前磁体系的磁化状态,文件名为“m0.omf”,接着再对这个这个文件中纳米线中心区域进行采样,如此空间范围变成了:x方向从-1nm到1nm,y方向从-30nm到30nm,z方向从0nm到1nm。那么使用avf2odt的命令行输入为:
tclsh oommf.tcl avf2odt //主命令
-average point //输出每个单元格的矢量值
-normalize 1 //输出结果归一化
-region -1e-9 - - 1e-9 - - //取样范围:Xmin Xmax,,,-表示文件中默认范围。
TODO_picture\矢量图处理\m0.omf //输入文件
-onefile "average_M.odt" //输出的odt文件名称
avf2odt工具的使用见手册第16章,这里不再解释了。于是用oommf的子程序mmGraph将生成的odt文件显示出来,如下图:
2.图4-2
没有激发自旋波时,测试磁体系在不同电流密度作用下,能保持稳定,neel畴壁不变形的临界电流密度。为了方便动态观察临界电流密度,对附录代码中关于设置电流的部分单独进行了这样改动:把电流密度大小设置为按模拟时间而阶段变化的,同时考虑到代码中的参数电流极化方向mpy只能在模拟运行之前修改,在模拟过程运行后就不能变化了。所以分为J>0和J<0两类情况:
第一组模拟:模拟时间为10ns,电流密度从0到100e10A/m2,按照每100ps增加1e10A/m2,在每次电流增加前,保存当前磁体系的状态,于是总共得到100个磁化文件。
第二组模拟:模拟时间为10ns,电流密度从0到-100e10A/m2,按照每100ps减少1e10A/m2,在每次电流减少前,保存当前磁体系的状态,于是总共得到100个磁化文件。
这两组模拟的使用的代码绝大部分都是相同的,就只有设置电流部分不同,比如第一组模拟的使用代码如下:
# MIF 2.1
#################
#author:YQYUN
#date:22/4/8
#desc:无自旋波,测试稳态畴壁的工作电流
#desc:电流密度从0到100e10,每100ps(一个阶段)线性增加,共100个阶段(10ns)
#desc:在每个阶段结束后保存磁化文件,模拟结束后,观察畴壁变形的临界电流密度
#################
set pi [expr {4*atan(1.0)}]
set mu0 [expr {4*$pi*1e-7}]
#使用时间驱动器的总共运行时间为10e-9s,每个阶段10e-11s
Parameter run_time 10e-9
Parameter stage_time 10e-11
set number_of_stages [expr {int(ceil($run_time/double($stage_time)))}]
#时间演化的时间步进最大为4e-13s
Parameter max_time_step 4e-13
#纳米线尺寸:2000*60*1nm
Parameter nanowire_x 2000
Parameter nanowire_y 60
Parameter nanowire_z 1
set nanowire_x [expr {$nanowire_x*1e-9}]
set nanowire_y [expr {$nanowire_y*1e-9}]
set nanowire_z [expr {$nanowire_z*1e-9}]
#单元格尺寸:1*1*1nm(单元格尺寸小于交换长度Lex=8.4nm)
Parameter xcell 1
Parameter ycell 1
Parameter zcell 1
set xcell [expr {$xcell*1e-9}]
set ycell [expr {$ycell*1e-9}]
set zcell [expr {$zcell*1e-9}]
#定义纳米线形状,按照DMI示例文件中的形式,需要使用Oxs_MultiAtlas类来定义容器
#注意,按照文章所述,这里需要平移磁体系的坐标系:
#把坐标原点移动到纳米线中心,
#即原来是xrange(0,2000nm),yrange(0,60nm),变成了xrange(-1000,1000nm),yrange(-30,30nm)
set nanowire_left [expr {-0.5 * $nanowire_x}]
set nanowire_right [expr {0.5 * $nanowire_x}]
set nanowire_down [expr {-0.5 * $nanowire_y}]
set nanowire_up [expr {0.5 * $nanowire_y}]
Specify Oxs_MultiAtlas:atlas [subst {
atlas { Oxs_BoxAtlas:world {
xrange {$nanowire_left $nanowire_right}
yrange {$nanowire_down $nanowire_up}
zrange {0 $nanowire_z}
name world
}}
}]
#定义网格尺寸
Specify Oxs_RectangularMesh:mesh [subst {
cellsize {$xcell $ycell $zcell}
atlas :atlas
}]
#定义交换能(15pJ/m)
Specify Oxs_UniformExchange {
A 15e-12
}
#定义单轴各向异性能(垂直方向,0.8MJ/m3)
Specify Oxs_UniaxialAnisotropy {
K1 0.8e6
axis {0 0 1}
}
#定义退磁能
Specify Oxs_Demag {}
#定义DMI能(3.5mJ/m2)
set D 3.5
set DD [expr {$D/1000}]
Specify Oxs_DMExchange6Ngbr:DMEx [subst {
default_D $DD
atlas :atlas
D {
world world $DD
}
}]
#定义阻尼系数,阻尼系数在纳米线中是沿x方向阶梯分布的:
#纳米线两端的阴影区域(长度200nm)范围内:
# -1000到-900nm,和900到1000nm内,阻尼系数最大,为0.5
# -900到-800nm,和800到900nm内,阻尼系数次之,为0.1
#中间区域的阻尼系数最小,为0.015
set shadeArea_alpha1 0.5
set shadeArea_alpha2 0.1
set middle_alpha 0.015
proc setAlphaScript { x y z } {
global nanowire_left nanowire_right nanowire_down nanowire_up
global shadeArea_alpha1 shadeArea_alpha2 middle_alpha
#分配左边阴影区域的阻尼系数
if {$x <= $nanowire_left + 200e-9 && $x >= $nanowire_left} {
if {$x <= $nanowire_left + 100e-9} {
return $shadeArea_alpha1
}
return $shadeArea_alpha2
}
#分配右边阴影区域的阻尼系数
if {$x >= $nanowire_right - 200e-9 && $x <= $nanowire_right} {
if {$x <= $nanowire_right - 100e-9} {
return $shadeArea_alpha1
}
return $shadeArea_alpha2
}
#分配中间区域的阻尼系数
return $middle_alpha
}
Specify Oxs_ScriptScalarField:alpha {
script setAlphaScript
script_args rawpt
atlas :atlas
}
#定义饱和磁化强度Ms(5.8e5A/m)
set Ms 5.8e5
###########时间演化的相关参数设置###########
#定义极化电流的属性(大小,方向)
set currentDensity 100e10
#定义电流的极化率(即自旋霍尔角),这里重金属为钽(P=0.13)
set polarization 0.13
#若电流密度为正(文章中为+x方向),且自旋霍尔角为正,则电子的极化方向指向-y
#若电流密度为负(文章中为-x方向),且自旋霍尔角为正,则电子的极化方向指向+y
set mpy -1
#查看oommf手册中7.3.4中Oxs_SpinXferEvolve说明文档
#类场项系数bj和类阻尼项系数aj之比,实际上在oommf中等于eps_prime/P*G,而G与Lambda有关
set eps_prime 0
#定义极化电流的属性(随时间(阶段数)变化)
proc setJProfile { stage } {
global number_of_stages
#电流大小随阶段数线性变化
return [expr {$stage * 1.0 / $number_of_stages}]
}
#定义时间演化器,设置SOT的作用效果
Specify Oxs_SpinXferEvolve:evolver [subst {
comment "按照不同区域定义阻尼系数"
alpha :alpha
J $currentDensity
J_profile setJProfile
J_profile_args stage
mp {0 $mpy 0}
P $polarization
comment "文章中Lambda为2"
Lambda 2
comment "设置类场项的系数"
eps_prime $eps_prime
comment "min_timestep的值不能大于4.3e-14,否则会得到错误的模拟结果"
comment "此处只规定一个范围,让演化器“自动的”取适当的时间步长"
min_timestep 0
max_timestep $max_time_step
}]
#定义驱动器
Specify Oxs_TimeDriver [subst {
evolver :evolver
mesh :mesh
comment "设置一个阶段的停止时间"
stopping_time $stage_time
comment "设置模拟包含的阶段数量"
stage_count $number_of_stages
Ms $Ms
comment "读取稳态畴壁的文件作为初始态"
m0 { Oxs_FileVectorField {
file "stable_neel_domain_wall.omf"
comment "平移矢量场文件中的坐标系,使它的坐标原点位于现在的纳米线的中心"
spatial_scaling { 1 1 1 }
spatial_offset { $nanowire_right $nanowire_up 0 }
comment "以上两行代码等效于一行代码:atlas :atlas"
}
}
comment "将checkpoint_interval设为-1,从而禁用检查点功能"
checkpoint_interval -1
}]
###########时间演化的相关参数设置###########
#在每个阶段结束后保存磁化文件
Destination Record mmArchive
Schedule Oxs_TimeDriver::Magnetization Record stage 1
第一组模拟结束后总共得到100个.omf磁化文件,那么现在只需依次查看这些文件,找出磁体系不能保持稳定的电流密度即可,当然,为了更加形象的展示磁体系随电流密度的变化,还需要把这些磁化文件转化为图片,再把这些图片制作成GIF、视频等。
首先使用oommf的命令行工具avf2ppm将磁化文件批量转化为.bmp图片,使用的命令类似如下所示:
tclsh oommf.tcl avf2ppm //主命令
-config TODO_picture\矢量图处理\无自旋波,测试稳态畴壁的工作电流\电流从0到100e10,电流每100ps线性(100个阶段)增加\图片显示配置文件\display(0to100e10).config //配置文件的路径
-format B24 //指定输出图片格式为BMP
-ipat TODO_picture\矢量图处理\无自旋波,测试稳态畴壁的工作电流\电流从0到100e10,电流每100ps线性(100个阶段)增加\待转换的磁化矢量文件\*.omf //输入文件所在的目录
-opatexp 待转换的磁化矢量文件 //使用正则表达式替换输出目录
-opatsub 转化后的图片 //使用正则表达式替换输出目录
oommf的命令行工具avf2ppm的使用方法同样在手册第16章,这里只对第二个参数-config需要的配置文件简单说明一下:参数值display(0to100e10).config是矢量图显示的配置文件,表示每个输入的磁化文件都根据这个显示配置文件输出图片。这个文件可以这样生成:利用oommf子程序mmDisp打开一个待转化的磁化文件,调整好mmDisp的显示参数,让图片的视觉效果最好,然后,利用File菜单将当前的显示参数保存到指定目录下即可。
接着将这100张图片制作成GIF图片,如下所示:
第二组电流密度为负的模拟,只需将代码中currentDensity 设置为-100e10,mpy设置为1即可。得到的100个磁化文件也是按照同样的方式转化为图片,最后制作的GIF图片如下:

当然,光凭肉眼是很难得到准确临界电流密度的,需要更加直观的得到电流密度的范围,可以从这100个磁化文件中提取纳米线的neel畴壁中的平均的磁化强度分量和电流密度的变化关系,在临界电流密度范围内,这些磁化分量的值都应该保持不变。这里利用oommf的命令行工具avf2odt来提取畴壁区域中的平均磁化强度分量:x从-1000nm到1000nm,y从-1nm到1nm,z从0nm到1nm空间范围内,使用的命令如下:
tclsh oommf.tcl avf2odt //主命令
-average space //整个区域的平均值
-region - -1e-9 - - 1e-9 - //指定取样区域范围,-表示文件的默认范围,
-index time s "abs($i) * 100e-12" //在odt文件插入时间列,$i表示当前输入文件的索引,即阶段数,每个阶段100ps
-index J A/m2 "abs($i) * 1e10" //在odt文件插入电流列,$i表示当前输入文件的索引,即阶段数,电流每个阶段增加1e10
-filesort "-ascii -increasing" //输入文件列表按照顺序增加来输入
-defaultpos 0 //odt文件中不生成位置坐标列
-ipat TODO_picture\矢量图处理\无自旋波,测试稳态畴壁的工作电流\电流从0到100e10,电流每100ps线性(100个阶段)增加\待转换的磁化矢量文件\*.omf //输入文件所在的目录
-onefile TODO_picture\矢量图处理\无自旋波,测试稳态畴壁的工作电流\电流从0到100e10,电流每100ps线性(100个阶段)增加\磁化文件转odt文件\0to100e10_DW_average_H.odt //输出的odt文件名称
-headers collapse //多个odt文件组合的一个odt文件,也只生成一组列标题
-normalize 1 //输出归一化的磁化分量
第一组模拟输出的0to100e10_DW_average_H.odt文件用mmGraph显示出来如下:
按照和第一组模拟类似的提取方式,第二组模拟电流密度为负的情况,将得到的.odt数据表文件用mmGraph显示出来如下:
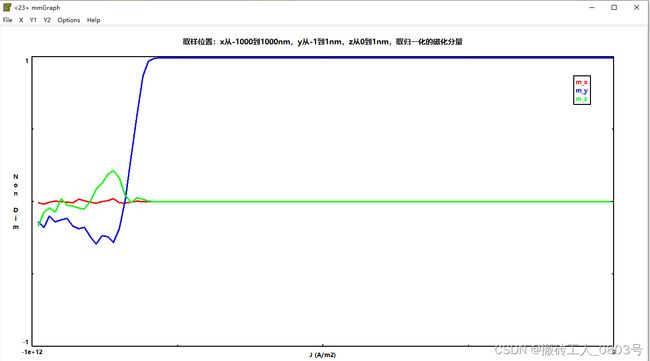
通过这两个图就很容易看出维持磁体系稳定,畴壁不变形的电流密度的范围,综合正负电流密度的两种情况,说明临界电流密度确实在1e11A/m2的数量级内。
以上两个模拟做起来还算简单,也没有对产生的数据进行太过复杂的处理。
3.Figure S1
电流密度J0为1e10A/m2,测试在SOT的类场项系数bJ和类阻尼项系数aJ的不同比值影响下,对激发的自旋波进行FFT分析。和上文对比,从这一部分开始的模拟便开始加入了自旋波。首先,需要康康代码的那个参数是用来设置类场项系数bJ和类阻尼项系数aJ的,参考oommf手册第7.3.4章Oxs_SpinXferEvolve的描述:
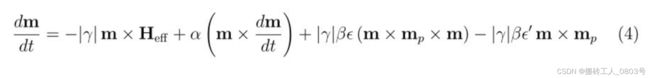
可以看出,bJ/aJ其实就等于eps_prime/(P*G),同时,在SOT中,这里的P被当做自旋霍尔角,磁体系的HM重金属层为钽(P=0.13),bJ/aJ的不同比值就对应参数eps_prime的值,那么需要模拟的6组参数:
第一组模拟:J=0,那么没有SOT的作用;
第二组模拟:J0为1e10A/m2,bJ/aJ=0,即eps_prime设置为0;
第三组模拟:J0为1e10A/m2,bJ/aJ=0.1/G,即eps_prime设置为0.013;
第四组模拟:J0为1e10A/m2,bJ/aJ=0.2/G,即eps_prime设置为0.026;
第五组模拟:J0为1e10A/m2,bJ/aJ=0.4/G,即eps_prime设置为0.052;
第六组模拟:J0为1e10A/m2,bJ/aJ=0.8/G,即eps_prime设置为0.104;
这里以第三组模拟为例子,使用的代码如下:
# MIF 2.1
#################
#author:YQYUN
#date:22/4/8
#desc:有自旋波,测试电流的SOT的类场项和类阻尼项对自旋波的影响
#desc:这是第三组测试:电流密度J为1e10,bj/aj=0.1/G
#desc:模拟时间为5ns,每2ps保存一次磁化文件(共2500个),模拟结束后,进行FFT分析
#################
set pi [expr {4*atan(1.0)}]
set mu0 [expr {4*$pi*1e-7}]
#使用时间驱动器的总共运行时间为5e-9s,每个阶段2e-12s
Parameter run_time 5e-9
Parameter stage_time 2e-12
set number_of_stages [expr {int(ceil($run_time/double($stage_time)))}]
#时间演化的时间步进最大为4e-14s
Parameter max_time_step 4e-14
#纳米线尺寸:2000*60*1nm
Parameter nanowire_x 2000
Parameter nanowire_y 60
Parameter nanowire_z 1
set nanowire_x [expr {$nanowire_x*1e-9}]
set nanowire_y [expr {$nanowire_y*1e-9}]
set nanowire_z [expr {$nanowire_z*1e-9}]
#单元格尺寸:1*1*1nm(单元格尺寸小于交换长度Lex=8.4nm)
Parameter xcell 1
Parameter ycell 1
Parameter zcell 1
set xcell [expr {$xcell*1e-9}]
set ycell [expr {$ycell*1e-9}]
set zcell [expr {$zcell*1e-9}]
#定义纳米线形状,按照DMI示例文件中的形式,需要使用Oxs_MultiAtlas类来定义容器
#注意,按照文章所述,这里需要平移磁体系的坐标系:
#把坐标原点移动到纳米线中心,
#即原来是xrange(0,2000nm),yrange(0,60nm),变成了xrange(-1000,1000nm),yrange(-30,30nm)
set nanowire_left [expr {-0.5 * $nanowire_x}]
set nanowire_right [expr {0.5 * $nanowire_x}]
set nanowire_down [expr {-0.5 * $nanowire_y}]
set nanowire_up [expr {0.5 * $nanowire_y}]
Specify Oxs_MultiAtlas:atlas [subst {
atlas { Oxs_BoxAtlas:world {
xrange {$nanowire_left $nanowire_right}
yrange {$nanowire_down $nanowire_up}
zrange {0 $nanowire_z}
name world
}}
}]
#定义网格尺寸
Specify Oxs_RectangularMesh:mesh [subst {
cellsize {$xcell $ycell $zcell}
atlas :atlas
}]
#定义交换能(15pJ/m)
Specify Oxs_UniformExchange {
A 15e-12
}
#定义单轴各向异性能(垂直方向,0.8MJ/m3)
Specify Oxs_UniaxialAnisotropy {
K1 0.8e6
axis {0 0 1}
}
#定义退磁能
Specify Oxs_Demag {}
#定义DMI能(3.5mJ/m2)
set D 3.5
set DD [expr {$D/1000}]
Specify Oxs_DMExchange6Ngbr:DMEx [subst {
default_D $DD
atlas :atlas
D {
world world $DD
}
}]
#定义阻尼系数,阻尼系数在纳米线中是沿x方向阶梯分布的:
#纳米线两端的阴影区域(长度200nm)范围内:
# -1000到-900nm,和900到1000nm内,阻尼系数最大,为0.5
# -900到-800nm,和800到900nm内,阻尼系数次之,为0.1
#中间区域的阻尼系数最小,为0.015
set shadeArea_alpha1 0.5
set shadeArea_alpha2 0.1
set middle_alpha 0.015
proc setAlphaScript { x y z } {
global nanowire_left nanowire_right nanowire_down nanowire_up
global shadeArea_alpha1 shadeArea_alpha2 middle_alpha
#分配左边阴影区域的阻尼系数
if {$x <= $nanowire_left + 200e-9 && $x >= $nanowire_left} {
if {$x <= $nanowire_left + 100e-9} {
return $shadeArea_alpha1
}
return $shadeArea_alpha2
}
#分配右边阴影区域的阻尼系数
if {$x >= $nanowire_right - 200e-9 && $x <= $nanowire_right} {
if {$x <= $nanowire_right - 100e-9} {
return $shadeArea_alpha1
}
return $shadeArea_alpha2
}
#分配中间区域的阻尼系数
return $middle_alpha
}
Specify Oxs_ScriptScalarField:alpha {
script setAlphaScript
script_args rawpt
atlas :atlas
}
#定义饱和磁化强度Ms(5.8e5A/m)
set Ms 5.8e5
###########时间演化的相关参数设置###########
#定义电流密度的属性(大小,方向)
set currentDensity 1e10
#定义电流的极化率(即自旋霍尔角),这里重金属为钽(P=0.13)
set polarization 0.13
#若电流密度为正(文章中为+x方向),且自旋霍尔角为正,则电子的极化方向指向-y
#若电流密度为负(文章中为-x方向),且自旋霍尔角为正,则电子的极化方向指向+y
set mpy -1
#查看oommf手册中7.3.4中Oxs_SpinXferEvolve说明文档
#类场项系数bj和类阻尼项系数aj之比,实际上在oommf中等于eps_prime/(P*G),而G与Lambda有关
set eps_prime 0.013
#定义时间演化器,设置SOT的作用效果
Specify Oxs_SpinXferEvolve:evolver [subst {
comment "按照不同区域定义阻尼系数"
alpha :alpha
J $currentDensity
mp {0 $mpy 0}
P $polarization
comment "文章中Lambda为2"
Lambda 2
comment "设置类场项的系数"
eps_prime $eps_prime
comment "每个时间步进最大为4e-14s"
max_timestep $max_time_step
}]
#定义驱动器
Specify Oxs_TimeDriver [subst {
evolver :evolver
mesh :mesh
comment "设置一个阶段的停止时间"
stopping_time $stage_time
comment "设置模拟包含的阶段数量"
stage_count $number_of_stages
Ms $Ms
comment "读取稳态畴壁的文件作为初始态"
m0 { Oxs_FileVectorField {
file "stable_neel_domain_wall.omf"
comment "平移矢量场文件中的坐标系,使它的坐标原点位于现在的纳米线的中心"
spatial_scaling { 1 1 1 }
spatial_offset { $nanowire_right $nanowire_up 0 }
comment "以上两行代码等效于一行代码:atlas :atlas"
}
}
comment "将矢量场输出的数据格式设置为ASCII文本格式(默认为b8格式)"
vector_field_output_format {text %#.17g}
comment "将checkpoint_interval设为-1,从而禁用检查点功能"
checkpoint_interval -1
}]
###########时间演化的相关参数设置###########
###########施加激发自旋波的外加磁场###########
#激发自旋波的微波磁场的振幅,这里的单位为mT,表示2000 Oe
set Happ 200
#激发自旋波的微波磁场的频率,这里的单位为GHz
set frequency 80
#t0=1e-15s
set t0 1e-15
#对初始的矢量场initialAntennaFiled进行变化,
#使其成为激发自旋波的外加磁场:H= Happ(xsincwt)
proc transformExcitationFiled { total_time } {
global frequency pi t0
set t [expr {$total_time + $t0}]
#计算w=2*pi*f,并把单位顺便转化为GHz
set w [expr {2 * $pi * $frequency * 1e9}]
set sinwt [expr {sin($w * $t)}]
set coswt [expr {cos($w * $t)}]
#计算x方向的磁场分量及其对时间的导数,其他方向为0
#即x方向H*sincwt
set Hx [expr {$sinwt / ($w * $t)}]
set dHx [expr {($w * $t * $coswt - $sinwt) / ($w * $t * $t)}]
#返回6个元素的列表,即变换矩阵的3个主对角元素及其3个导数
return [list $Hx 0 0 $dHx 0 0]
}
#指定天线区域的矢量场(后面转化为磁场):H= (Happ 0 0),其他区域H=(0 0 0)
proc initialAntennaFiled { x y z } {
global nanowire_left Happ
#天线距离纳米线左端200nm,天线宽度为4nm
if {$x >= $nanowire_left + 200e-9 && $x <= $nanowire_left + 200e-9 + 4e-9} {
return "$Happ 0 0"
}
#其他区域无外加磁场
return "0 0 0"
}
#使用脚本指定天线区域的矢量场
Specify Oxs_ScriptVectorField:antennaFiled {
script initialAntennaFiled
script_args rawpt
atlas :atlas
}
#使用此类可生成任意(局域,时变)的外加磁场
Specify Oxs_TransformZeeman [subst {
field :antennaFiled
comment "函数返回6个元素,是3个主对角元素及其3个导数"
type diagonal
script transformExcitationFiled
script_args total_time
comment "将默认单位A/m换算为mT"
multiplier [expr {0.001/$mu0}]
comment "将stage_count设为0(默认值),让模拟的所有阶段都存在该塞曼能"
stage_count 0
}]
##########施加激发自旋波的外加磁场###########
#每个阶段固定为2ps,模拟总共运行5ns
#每2*1=2ps保存一次磁化文件,应该生成2500个磁化文件
Destination Record mmArchive
Schedule Oxs_TimeDriver::Magnetization Record stage 1
模拟结束得到2500个磁化文件之后,那么问题来了,如何对这些磁化文件进行FFT分析呢?
好在不需要自己动脑筋,早已有现成的程序可以做到这一点。那么现在就暂且搁置这一部分的内容,先介绍下这款程序,等学会使用后,再回过头来继续分析。
二、暂别
1.FFT分析程序包:MFA简介
MuFA,它的介绍文章和下载链接DOI:10.1016/j.cpc.2019.06.023。它是由电子科大任志伟大佬开发的基于Python的微磁数据后处理程序包,使用方法请参考大佬的硕士论文《耦合型自旋波功能器件 》第三章,和程序包附带的说明文档。
MFA是这个程序包的两个组成部分之一,主要可用于两种类型的一维傅里叶分析:自旋波的归一化频率成分曲线;用一个色彩图来可视化自旋波功率沿波矢方向的空间分布情况。也可用于二维傅里叶分析,即自旋波色散曲线的计算。
2.使用练习MFA
说明文档中使用的示例正是DOI: 10.1103/PhysRevLett.102.127202这一篇文章中的P=P1+P2=9nm+9nm=18nm的情况。具体内容请参考原文,这里不再描述。程序包附带的示例代码是用于Mumax模拟的,但没有用于oommf模拟的代码,如下:
//output directory: E:\MuFA\SBG\classic dispersion.out/
SetMesh(1000, 20, 1, 1.5e-09, 1.5e-09, 1e-08, 0, 0, 0)
a := Cuboid(1500e-9, 30e-9, 10e-9)
b := Cuboid(9e-9, 3e-9, 10e-9).Transl(-245.5e-9, 13.5e-9, 0)
c := Cuboid(9e-9, 3e-9, 10e-9).Transl(-245.5e-9, -13.5e-9, 0)
p := 18e-9
i_start1 := 1
i_limit1 := 57
i_step1 := 1
for i := i_start1; i < i_limit1; i += i_step1 {
a = a.Sub(b).Sub(c)
b = b.Transl(p, 0, 0)
c = c.Transl(p, 0, 0)
}
SetGeom(a)
DefRegion(1, XRange(-750e-9, -747e-9))
DefRegion(2, XRange(-747e-9, 744e-9))
DefRegion(3, XRange(744e-9, 750e-9))
m = Uniform(1, 0.0001, 0)
alpha.SetRegion(1, 0.01)
alpha.SetRegion(2, 0.01)
alpha.SetRegion(3, 0.5)
Msat = 8.6e5
Aex = 1.3e-11
OutputFormat = OVF2_TEXT
Relax()
amp_B1 := 1
f_B1 := 2 * pi * 100e9
B_ext.SetRegion(1, vector(0, amp_B1*sin(f_B1*t+1e-13)/(f_B1*t+1e-13), 0))
AutoSave(m, 2e-12)
Run(5e-9)
为了练习使用这个程序包,于是结合文章和Mumax代码,将它改写成为适用于oommf模拟的代码,如下:
# MIF 2.1
#################
#author:YQYUN
#date:22/4/20
#desc:宽度调制纳米线波导中偶极交换自旋波磁能隙的物理起源和一般控制
#desc:周期性结构总长度P=18nm,P1=P2=9nm
#desc:模拟时间5ns,每2ps(即1个阶段)保存磁化图,模拟结束后,进行自旋波分析
#################
set pi [expr {4*atan(1.0)}]
set mu0 [expr {4*$pi*1e-7}]
#使用时间驱动器的总共运行时间为5e-9s
Parameter run_time 5e-9
#每个阶段2e-12s
Parameter stage_time 2e-12
set number_of_stages [expr {int(ceil($run_time/double($stage_time)))}]
#时间演化的最大时间步进为4e-14s
Parameter max_time_step 4e-14
#纳米线尺寸:1500*30*10nm
Parameter nanowire_x 1500
Parameter nanowire_y 30
Parameter nanowire_z 10
set nanowire_x [expr {$nanowire_x*1e-9}]
set nanowire_y [expr {$nanowire_y*1e-9}]
set nanowire_z [expr {$nanowire_z*1e-9}]
#单元格尺寸:1.5*1.5*10nm
Parameter xcell 1.5
Parameter ycell 1.5
Parameter zcell 10
set xcell [expr {$xcell*1e-9}]
set ycell [expr {$ycell*1e-9}]
set zcell [expr {$zcell*1e-9}]
#定义纳米线形状,分为3个区域:天线区域,波导区域,周期性结构区域
#天线区域:3*30*10nm
Parameter antennaLength 3
#波导区域:(500-3)*30*10nm
Parameter waveguideLength 497
#周期性结构区域:1000*30*10,其中周期性结构长度P=P1+P2=9+9=18nm,窄的24nm,宽的30nm
Parameter periodP1Length 9
Parameter periodP2Length 9
Parameter periodP1Width 24
Parameter periodP2Width 30
set antennaLength [expr {$antennaLength*1e-9}]
set waveguideLength [expr {$waveguideLength*1e-9}]
set periodP1Length [expr {$periodP1Length*1e-9}]
set periodP2Length [expr {$periodP2Length*1e-9}]
set periodP1Width [expr {$periodP1Width*1e-9}]
set periodP2Width [expr {$periodP2Width*1e-9}]
proc setRegion { x y z } {
global nanowire_y
global antennaLength waveguideLength
global periodP1Length periodP2Length periodP1Width periodP2Width
#分配天线的区域
if {$x <= $antennaLength} {
return 1
} elseif {$x <= ($antennaLength + $waveguideLength)} {
#分配波导的区域
return 2
} else {
#分配周期性结构区域
#得到该单元格位于一个周期性结构的相对x坐标
set rx [expr {fmod(($x - $antennaLength - $waveguideLength),($periodP1Length + $periodP2Length))}]
#若该单元格位于窄的结构
if {$rx <= $periodP1Length} {
#定义窄结构的上(y2)下(y1)边缘
set y1 [expr {($nanowire_y - $periodP1Width) / 2}]
set y2 [expr {(($nanowire_y - $periodP1Width) / 2) + $periodP1Width}]
if {$y >= $y1 && $y <= $y2} {
return 3
} else {
#其余部分是缺陷
return 0
}
} else {
#若该单元格位于宽的结构
#定义宽结构的上(y2)下(y1)边缘
set y1 [expr {($nanowire_y - $periodP2Width) / 2}]
set y2 [expr {(($nanowire_y - $periodP2Width) / 2) + $periodP2Width}]
if {$y >= $y1 && $y <= $y2} {
return 3
} else {
#其余部分是缺陷
return 0
}
}
}
return 0
}
#定义纳米线形状
Specify Oxs_ScriptAtlas:atlas [subst {
xrange { 0 $nanowire_x }
yrange { 0 $nanowire_y }
zrange { 0 $nanowire_z }
regions { antennaRegion waveguideRegion periodRegion }
script_args rawpt
script setRegion
}]
#定义网格尺寸
Specify Oxs_RectangularMesh:mesh [subst {
cellsize {$xcell $ycell $zcell}
atlas :atlas
}]
#定义交换能(13pJ/m)
Specify Oxs_UniformExchange {
A 13e-12
}
# #定义一个标量场对象来为磁体系的不同区域分配交换系数
# Specify Oxs_AtlasScalarField:exchange {
# atlas :atlas
# default_value 0
# values {
# antennaRegion 13e-12
# waveguideRegion 13e-12
# periodRegion 13e-12
# }
# }
# #定义交换项,其中的交换系数是逐单元格指定的
# Specify Oxs_ExchangePtwise {
# A :exchange
# }
#定义退磁能
Specify Oxs_Demag {}
#定义阻尼系数,有两个低阻尼区域为0.01,一个高阻尼区域为0.5
set alpha1 0.01
set alpha2 0.01
set alpha3 0.5
proc setAlpha {x y z} {
global alpha1 alpha2 alpha3
global nanowire_x
if {$x <= 3e-9 } {
return $alpha1
} elseif {$x<= ($nanowire_x - 6e-9)} {
return $alpha2
} else {
return $alpha3
}
}
#定义一个标量场对象来设置阻尼系数
Specify Oxs_ScriptScalarField:alpha {
script setAlpha
script_args rawpt
atlas :atlas
}
#定义饱和磁化强度Ms(8.6e5A/m)
set Ms 8.6e5
###########时间演化的相关参数设置###########
#定义演化器(龙格-库塔时间演化器)
Specify Oxs_RungeKuttaEvolve:evolver [subst {
comment "按照不同区域定义阻尼系数"
alpha :alpha
comment "每个时间步进最大为4e-14s"
max_timestep $max_time_step
}]
#定义驱动器
Specify Oxs_TimeDriver [subst {
evolver :evolver
mesh :mesh
comment "设置一个阶段的停止时间"
stopping_time $stage_time
comment "设置包含的总阶段数量"
stage_count $number_of_stages
comment "设置磁体系的不同区域的饱和磁化强度,缺陷区域为0"
Ms {Oxs_AtlasScalarField {
atlas :atlas
default_value 0
values {
antennaRegion $Ms
waveguideRegion $Ms
periodRegion $Ms
}
}
}
comment "初始磁化"
m0 {1 0.0001 0}
comment "将矢量场输出的数据格式设置为ASCII文本格式(默认为b8格式)"
vector_field_output_format {text %#.17g}
comment "将checkpoint_interval设为-1,从而禁用检查点功能"
checkpoint_interval -1
}]
# m0 {Oxs_AtlasVectorField {
# atlas :atlas
# default_value {0 0 0}
# values {
# antennaRegion {1 0.0001 0}
# waveguideRegion {1 0.0001 0}
# periodRegion {1 0.0001 0}
# }
# }
###########时间演化的相关参数设置###########
###########施加激发自旋波的外加磁场###########
#激发自旋波的微波磁场的振幅,这里的单位为mT,表示10000 Oe
set Happ 1000
#激发自旋波的微波磁场的频率,这里的单位为GHz
set frequency 100
#t0=0.1ps
set t0 1e-13
#对初始的矢量场initialAntennaFiled进行变化,
#使其成为激发自旋波的外加磁场:H= Happ(ysinc(wt))
proc transformExcitationFiled { total_time } {
global frequency pi t0
#计算w=2*pi*f,并把单位顺便转化为GHz
set w [expr {2 * $pi * $frequency * 1e9}]
set wt_t0 [expr {$w * $total_time + $t0}]
set sinwt_t0 [expr {sin($wt_t0)}]
set coswt_t0 [expr {cos($wt_t0)}]
#计算y方向的磁场分量及其对时间的导数,其他方向为0
#即y方向sinc(wt)
set Hy [expr {$sinwt_t0 / $wt_t0}]
set dHy [expr {($coswt_t0 * $w * $wt_t0 - $sinwt_t0 * $w) / ($wt_t0 * $wt_t0)}]
#返回6个元素的列表,即变换矩阵的3个主对角元素及其3个导数
return [list 0 $Hy 0 0 $dHy 0]
}
#指定天线区域的矢量场(后面转化为磁场):H= (0 Happ 0),其他区域H=(0 0 0)
proc initialAntennaFiled { x y z } {
global antennaLength Happ
if {$x <= $antennaLength} {
return "0 $Happ 0"
}
#其他区域无外加磁场
return "0 0 0"
}
#使用脚本指定天线区域的矢量场
Specify Oxs_ScriptVectorField:antennaFiled {
script initialAntennaFiled
script_args rawpt
atlas :atlas
}
#使用此类可生成任意(局域,时变)的外加磁场
Specify Oxs_TransformZeeman [subst {
field :antennaFiled
comment "函数返回6个元素,是3个主对角元素及其3个导数"
type diagonal
script transformExcitationFiled
script_args total_time
comment "将默认单位A/m换算为mT"
multiplier [expr {0.001/$mu0}]
comment "将stage_count设为0(默认值),让模拟的所有阶段都存在该塞曼能"
stage_count 0
}]
##########施加激发自旋波的外加磁场###########
#每个阶段固定为2ps,模拟总共运行5ns,应该生成2500个磁化文件
Destination Record mmArchive
Schedule Oxs_TimeDriver::Magnetization Record stage 1
从这里可以看出oommf代码和Mumax代码的部分区别,除开一些变量的定义和注释外,oommf的代码量还是比较多的。除此之外,两者施加时变的外加磁场的方式差别也是蛮大的。
这里简单说明一下代码中两个值得注意的地方:
①
comment "将矢量场输出的数据格式设置为ASCII文本格式(默认为b8格式)"
vector_field_output_format {text %#.17g}
这个语句表示将输出的矢量场数据格式设置为文本格式,因为不管是碳基生物还是MFA程序都识别不了默认b8格式,但是采用b8格式的唯一优点就是节省存储空间,它比文本格式的磁化文件大约小三分之一。此外,请将.mif文件放在不包含中文字符的目录下运行,否则生成的磁化文件的desc注释里有中文,MFA程序也识别不了中文。
如果你忘了添加这个格式转换语句,得到一堆b8格式的矢量场数据,别担心,还有补救的方法,那就是利用oommf的命令行工具avf2ovf将b8格式的.omf文件转化为文本格式的,通用的.ovf矢量场文件。但是这个命令行工具avf2ovf有一个缺点,就是不支持批量转换文件,也就是说一条命令就只能转换一个文件,所以我们需要利用批处理命令的循环指令自动生成很多的命令,让这个工具能将指定目录下的所有.omf文件全部转换成.ovf文件。
批处理命令如下:
@ rem 请将该批处理文件放在oommf安装根目录,并修改后缀名为.bat
@ set number=0
@ rem 开启变量延迟
@ setlocal enabledelayedexpansion
@ rem 注意待处理的磁化文件相对于本文件的位置
@ set inFileFilter=TODO_picture\矢量图处理\宽度调制纳米线波导中偶极交换自旋波磁能隙的物理起源和一般控制\待转换的磁化矢量文件\*.omf
@ rem 以下命令是使用avf2ovf的命令,请先理解它的命令参数
@ rem 输出文件的路径
@ set outFileDir=TODO_picture\矢量图处理\宽度调制纳米线波导中偶极交换自旋波磁能隙的物理起源和一般控制\转化后的OVF文件\
@ rem 输出文件的前缀和后缀
@ set outFileBaseName=m_
@ set outFileApend=.ovf
@ rem %%i是输入omf文件的名称
@ rem outFileFullName是输出ovf文件的名称
for %%i in (%inFileFilter%) do (
@ set outFileFullName=%outFileDir%%outFileBaseName%!number!%outFileApend%
@ set /A number+=1
tclsh oommf.tcl avf2ovf ^
-dataformat text -fileformat ovf 2 ^
%%i !outFileFullName!
)
②
代码中关于交换能,和初始磁化m0的两处注释。表示定义磁体系的缺陷区域的属性,无论是按区域设置这两个参数,还是将这两个参数设置为空间均匀分布。在这两种情况下,分别进行模拟,最后对磁化文件进行FFT分析后,发现得到的图片都是一样的,可见这两个参数并不是设置磁体系的缺陷的关键参数。那么磁体系的缺陷是如何定义呢?其实只需将缺陷区域的饱和磁化强度Ms设置为0即可。
oommf在调试模拟的时候,要确保自己施加的外加磁场是正确的,所以可能需要把时变的外加磁场提取出来验证一下。可以在上面的代码末尾添加保存外加磁场的语句,也可以在模拟开始前,手动在求解器的输出计划中选择保存的场,模拟结束后,就可以得到2500个后缀为.omf的磁化文件,和2500个后缀为.ohf的保存外加磁场的矢量场文件。使用命令行工具avf2odt提取天线区域内的外加磁场随时间的变化关系,使用的命令如下:
tclsh oommf.tcl avf2odt //主命令
-average space //整个区域的平均值
-region - - - 3e-9 - - //指定取样区域范围,-表示文件的默认范围,
-index time s "abs($i) * 2e-12" //在odt文件插入时间列,$i表示当前输入文件索引,即阶段数,每个阶段2ps
-filesort "-ascii -increasing" //输入文件列表按照顺序增加来输入
-defaultpos 0 //odt文件中不生成位置坐标列
-ipat TODO_picture\矢量图处理\宽度调制纳米线波导中偶极交换自旋波磁能隙的物理起源和一般控制\待转换的磁化矢量文件\*.ohf //输入文件所在的目录
-onefile TODO_picture\矢量图处理\宽度调制纳米线波导中偶极交换自旋波磁能隙的物理起源和一般控制\average_H.odt //输出的odt文件名称
-headers collapse //多个odt文件组合的一个odt文件,也只生成一组列标题
//不要输出归一化的磁化分量
将输出的average_H.odt文件用mmGraph显示出来,如下所示,正是sinc函数,说明塞曼能设置正确:

接下来,需要对2500个.omf磁化文件进行FFT分析,将MFA程序包的示例结果和自己的模拟结果对比如下:
自己得到的模拟结果:
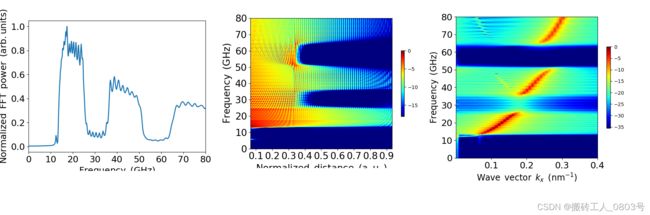
仔细观察的话,可以看到自己得到的第一张和第三张图片与示例图有亿点点差异,曲线在f=10GHz的右边部分不太平滑,不过我也不知道问题出在哪里,难道是求解器的时间步长取小了?问题应该不大,,,吧。

三、重逢
3.Figure S1
现在是峰回路转,经过一个小插曲,又回到第一篇文章了,按照和上文类似的方法,先检验一下天线区域中施加的外加磁场是否符合预想的情况。这里补充一下第一.3节所述,选择六组模拟中的任意一组,在模拟开始前,额外把施加的外加磁场按相同的时间间隔保存起来,那么也得到了2500个.ohf文件。利用avf2odt提取天线区域中的平均外加磁场,并得到它随时间的变化关系。avf2odt使用的命令如下:
tclsh oommf.tcl avf2odt //主命令
-average space //整个区域的平均值
-region -800e-9 - - -796e-9 - - //指定区域范围,-表示文件的默认范围
-index time s "abs($i) * 2e-12" //在odt文件插入时间列,$i表示当前输入文件的索引
-filesort "-ascii -increasing" //输入文件列表按照顺序增加来输入
-defaultpos 0 //odt文件中不生成位置坐标列
-ipat TODO_picture\矢量图处理\自旋波(振幅2000Oe,频率80GHz),电流大小1e10,测试SOT的aj和bj比例的影响\施加的外加磁场随时间的变化\待转换的磁化矢量文件\*.ohf //输入文件所在的目录
-onefile TODO_picture\矢量图处理\自旋波(振幅2000Oe,频率80GHz),电流大小1e10,测试SOT的aj和bj比例的影响\施加的外加磁场随时间的变化\磁化文件转odt文件\averageH_t.odt //输出的odt文件名称
-headers collapse //多个odt文件组合的一个odt文件,也只生成一组列标题
//不要输出归一化的磁化分量
那么将得到的averageH_t.odt数据表文件用mmGraph显示出来,如下图所示:
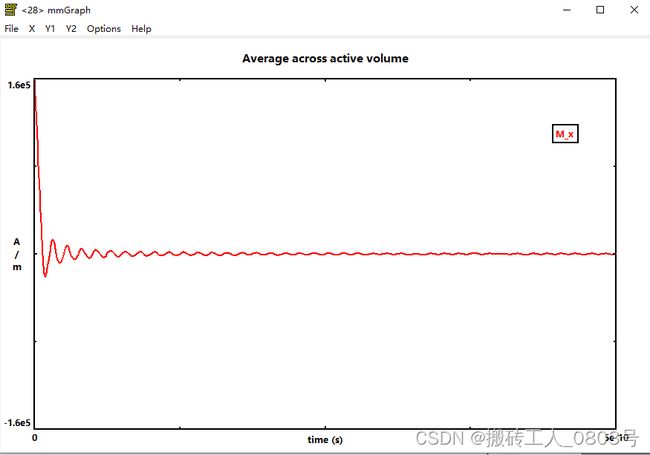
画一个标准的sinc函数:
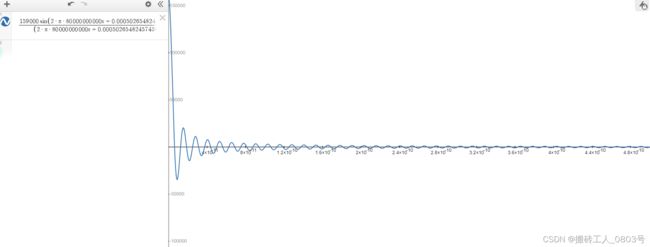
对比两张图说明,这里施加的外加磁场确实是2000OeXsinc(2XpiX80GHzX(t+1e-15)),和设想的一样。
在模拟时间为0.4ns时,得到的一个磁化文件:

利用MFA,把一维FFT和二维FFT 的采样区域都设为:
x_start, x_end = 200e-9,1800e-9
y_start, y_end = 29e-9,31e-9
z_start, z_end = 0,1e-9
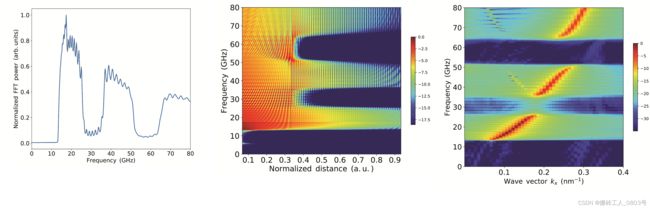
将第三组模拟得到的2500个磁化文件进行一维的FFT处理,得到自旋波的功率和频率的关系如下图所示:

对比Figure S1,简直完全不一样啊!虽然利用MFA生成的图的纵坐标单位是归一化的,但就连曲线的变化趋势都不一样,这说明不知道又是哪里出错了。。。

难道是时间演化器的时间步进大小(即时间步长)和模拟时间设置错了吗?于是,作为对比,在模拟第一组J=0时,我尝试将第一组模拟的时间演化器的步长固定为4e-14s,然后每迭代100次(即间隔4ps)保存一次磁化文件,模拟时间改为10ns。利用MFA对生成的磁化文件进行一维FFT,第一组J=0的结果如下:

然后对比一下不是固定的时间步长,模拟时间5ns:

对比一下两者在2.5-5GHz之间有一点差异,但都对不上Figure S1,这么说的话,似乎不是代码中设置的时间步长和模拟时间的问题。
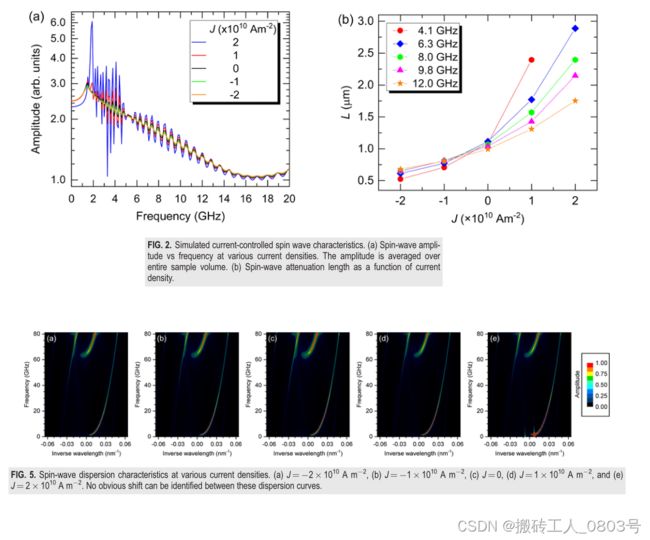
4.FIG.2 (a)
当忽略SOT的类场项作用时,测试在不同电流密度作用下时,对激发的自旋波进行FFT分析。在这一模拟中,电流密度J分别取值2e10,1e10,0,-1e10,-2e10A/m2,总共分为五组参数来模拟,外加磁场依然和上文一样采用sinc函数来激发自旋波,对模拟生成的磁化数据的处理和Figure S1一样。但注意,从这一小节及之后的模拟,对于SOT的作用都只考虑类阻尼项,而不考虑类场项的效果,即把类场项系数(eps_prime)设置为0。那么这五组模拟是:
第一组模拟:J=2e10A/m2,eps_prime=0。
第二组模拟:J=1e10A/m2,eps_prime=0。
第三组模拟:J=0,eps_prime=0。
第四组模拟:J=-1e10A/m2,eps_prime=0。
第五组模拟:J=-2e10A/m2,eps_prime=0。
很明显,在这五组模拟中,第二组和第三组模拟对应Figure S1的第一组和第二组模拟。所以这里只需要对第一、四、五组进行模拟即可,那么这里以第四组J=-1e10为例,使用的代码和上文类似,改动的地方如下:
# MIF 2.1
#################
#author:YQYUN
#date:22/4/8
#desc:有自旋波,测试不同电流密度对自旋波的影响
#desc:这是第四组测试:电流密度J为-1e10,eps_prime为0
#desc:模拟时间为5ns,每2ps保存一次磁化文件(共2500个),模拟结束后,进行FFT分析
#################
#定义电流密度的属性(大小,方向)
set currentDensity -1e10
#定义电流的极化率(即自旋霍尔角),这里重金属为钽(P=0.13)
set polarization 0.13
#若电流密度为正(文章中为+x方向),且自旋霍尔角为正,则电子的极化方向指向-y
#若电流密度为负(文章中为-x方向),且自旋霍尔角为正,则电子的极化方向指向+y
set mpy 1
#查看oommf手册中7.3.4中Oxs_SpinXferEvolve说明文档
#类场项系数bj和类阻尼项系数aj之比,实际上在oommf中等于eps_prime/(P*G),而G与Lambda有关
set eps_prime 0
利用MFA对生成的2500个磁化文件进行一维FFT处理,如果不出意外的话,那就是出意外了:


5.FIG.2 (b)
当忽略SOT的类场项作用时,测试不同频率的自旋波在不同电流密度下的衰减长度。遇到这个模拟的时候,我就有点懵逼了,我只知道波的衰减长度表示的是波在媒质中传播时,振幅减少为原来的1/e时,波所传播的距离。但在这个磁体系中如何生成特定频率的自旋波呢?文章附录的oommf代码里似乎也没有关于衰减长度的内容。好吧,由于我现阶段的知识储备不够,我也不知道其中的道道,所以就随着自己的理所当然的想法来试一试吧。我的想法就是,把在天线区域施加的外加磁场的形式从2000Oe,80GHz的sinc函数改变为了不同频率的sin函数,但是保持振幅都为2000Oe。那么,这一小节可以分为五大组模拟:
第一大组:外加磁场为2000Oe,4.1GHz的sin函数。
第二大组:外加磁场为2000Oe,6.3GHz的sin函数。
第三大组:外加磁场为2000Oe,8GHz的sin函数。
第四大组:外加磁场为2000Oe,9.8GHz的sin函数。
第五大组:外加磁场为2000Oe,12GHz的sin函数。
接着还要考虑特定频率下不同的电流密度(J=2e10,1e10,0,-1e10,-2e10A/m2)的情况,如上文所述,代码中与电流密度正负有关的参数mpy只能在模拟运行之前修改,在模拟运行后就不能改变了。FIG.2 (b)中总共有5种频率X5种电流密度=25个数据点。这里为了简单起见,再次将每一大组模拟再细分为两小组模拟:第一小组模拟电流密度J>=0,第二小组模拟电流密度J<0。
在J>=0的情况下,把电流密度设置为随着模拟时间而阶梯增加,电流密度从0到2e10,每2ns 增加1e10,总共模拟6ns。在J<0的情况下,把电流密度设置为随着模拟时间阶梯减小,电流密度从-1e10到-2e10,每2ns 减少1e10,总共模拟4ns。两种情况下,都是间隔0.5ns保存一次磁体系的状态。
那么总共有10组模拟。这里以第一大组的第一小组为例,即外加磁场为2000Oe,4.1GHz的sin函数,电流密度从0到2e10,每2ns 增加1e10,总共模拟6ns。使用的代码如下:
# MIF 2.1
#################
#author:YQYUN
#date:22/4/8
#desc:使用不同频率的sin形式的外加磁场激发自旋波
#desc:这是第一组测试:外加磁场频率为4.1GHz,
#desc:电流密度J随时间变化,从0到2e10每2ns增加1e10(每种电流密度下有4个磁化文件),eps_prime为0
#desc:模拟时间为6ns,每1个阶段(0.5ns)保存一次磁化文件,模拟结束后,计算平均衰减长度
#################
set pi [expr {4*atan(1.0)}]
set mu0 [expr {4*$pi*1e-7}]
#使用时间驱动器的总共运行时间为6e-9s
Parameter run_time 6e-9
#每个阶段0.5e-9s
Parameter stage_time 0.5e-9
set number_of_stages [expr {int(ceil($run_time/double($stage_time)))}]
#时间演化的最大时间步进为4e-14s
Parameter max_time_step 4e-14
#纳米线尺寸:2000*60*1nm
Parameter nanowire_x 2000
Parameter nanowire_y 60
Parameter nanowire_z 1
set nanowire_x [expr {$nanowire_x*1e-9}]
set nanowire_y [expr {$nanowire_y*1e-9}]
set nanowire_z [expr {$nanowire_z*1e-9}]
#单元格尺寸:1*1*1nm(单元格尺寸小于交换长度Lex=8.4nm)
Parameter xcell 1
Parameter ycell 1
Parameter zcell 1
set xcell [expr {$xcell*1e-9}]
set ycell [expr {$ycell*1e-9}]
set zcell [expr {$zcell*1e-9}]
#定义纳米线形状,按照DMI示例文件中的形式,需要使用Oxs_MultiAtlas类来定义容器
#注意,按照文章所述,这里需要平移磁体系的坐标系:
#把坐标原点移动到纳米线中心,
#即原来是xrange(0,2000nm),yrange(0,60nm),变成了xrange(-1000,1000nm),yrange(-30,30nm)
set nanowire_left [expr {-0.5 * $nanowire_x}]
set nanowire_right [expr {0.5 * $nanowire_x}]
set nanowire_down [expr {-0.5 * $nanowire_y}]
set nanowire_up [expr {0.5 * $nanowire_y}]
Specify Oxs_MultiAtlas:atlas [subst {
atlas { Oxs_BoxAtlas:world {
xrange {$nanowire_left $nanowire_right}
yrange {$nanowire_down $nanowire_up}
zrange {0 $nanowire_z}
name world
}}
}]
#定义网格尺寸
Specify Oxs_RectangularMesh:mesh [subst {
cellsize {$xcell $ycell $zcell}
atlas :atlas
}]
#定义交换能(15pJ/m)
Specify Oxs_UniformExchange {
A 15e-12
}
#定义单轴各向异性能(垂直方向,0.8MJ/m3)
Specify Oxs_UniaxialAnisotropy {
K1 0.8e6
axis {0 0 1}
}
#定义退磁能
Specify Oxs_Demag {}
#定义DMI能(3.5mJ/m2)
set D 3.5
set DD [expr {$D/1000}]
Specify Oxs_DMExchange6Ngbr:DMEx [subst {
default_D $DD
atlas :atlas
D {
world world $DD
}
}]
#定义阻尼系数,阻尼系数在纳米线中是沿x方向阶梯分布的:
#纳米线两端的阴影区域(长度200nm)范围内:
# -1000到-900nm,和900到1000nm内,阻尼系数最大,为0.5
# -900到-800nm,和800到900nm内,阻尼系数次之,为0.1
#中间区域的阻尼系数最小,为0.015
set shadeArea_alpha1 0.5
set shadeArea_alpha2 0.1
set middle_alpha 0.015
proc setAlphaScript { x y z } {
global nanowire_left nanowire_right nanowire_down nanowire_up
global shadeArea_alpha1 shadeArea_alpha2 middle_alpha
#分配左边阴影区域的阻尼系数
if {$x <= $nanowire_left + 200e-9 && $x >= $nanowire_left} {
if {$x <= $nanowire_left + 100e-9} {
return $shadeArea_alpha1
}
return $shadeArea_alpha2
}
#分配右边阴影区域的阻尼系数
if {$x >= $nanowire_right - 200e-9 && $x <= $nanowire_right} {
if {$x <= $nanowire_right - 100e-9} {
return $shadeArea_alpha1
}
return $shadeArea_alpha2
}
#分配中间区域的阻尼系数
return $middle_alpha
}
Specify Oxs_ScriptScalarField:alpha {
script setAlphaScript
script_args rawpt
atlas :atlas
}
#定义饱和磁化强度Ms(5.8e5A/m)
set Ms 5.8e5
###########时间演化的相关参数设置###########
#定义电流密度的属性(大小,方向)
set currentDensity 2e10
#定义电流的极化率(即自旋霍尔角),这里重金属为钽(P=0.13)
set polarization 0.13
#若电流密度为正(文章中为+x方向),且自旋霍尔角为正,则电子的极化方向指向-y
#若电流密度为负(文章中为-x方向),且自旋霍尔角为正,则电子的极化方向指向+y
set mpy -1
#查看oommf手册中7.3.4中Oxs_SpinXferEvolve说明文档
#类场项系数bj和类阻尼项系数aj之比,实际上在oommf中等于eps_prime/(P*G),而G与Lambda有关
set eps_prime 0
#电流密度随时间变化
proc setJProfile { total_time } {
#在0-2ns内,J=0
if {$total_time <= 2e-9} {
return 0
} elseif {$total_time <= 4e-9} {
#在2-4ns内,J=1e10
return 0.5
} elseif {$total_time <= 6e-9} {
#在4-6ns内,J=2e10
return 1
}
}
#定义时间演化器,设置SOT的作用效果
Specify Oxs_SpinXferEvolve:evolver [subst {
comment "按照不同区域定义阻尼系数"
alpha :alpha
J $currentDensity
J_profile setJProfile
J_profile_args total_time
mp {0 $mpy 0}
P $polarization
comment "文章中Lambda为2"
Lambda 2
comment "设置类场项的系数"
eps_prime $eps_prime
comment "min_timestep的值不能大于4.3e-14,否则会得到错误的模拟结果"
comment "此处只规定一个范围,让演化器“自动的”取适当的时间步长"
min_timestep 0
max_timestep $max_time_step
}]
#定义驱动器
Specify Oxs_TimeDriver [subst {
evolver :evolver
mesh :mesh
comment "设置一个阶段的停止时间"
stopping_time $stage_time
comment "设置模拟包含的阶段数量"
stage_count $number_of_stages
Ms $Ms
comment "读取稳态畴壁的文件作为初始态"
m0 { Oxs_FileVectorField {
file "stable_neel_domain_wall.omf"
comment "平移矢量场文件中的坐标系,使它的坐标原点位于现在的纳米线的中心"
spatial_scaling { 1 1 1 }
spatial_offset { $nanowire_right $nanowire_up 0 }
comment "以上两行代码等效于一行代码:atlas :atlas"
}
}
comment "将矢量场输出的数据格式设置为ASCII文本格式(默认为b8格式)"
vector_field_output_format {text %#.17g}
comment "将checkpoint_interval设为-1,从而禁用检查点功能"
checkpoint_interval -1
}]
###########时间演化的相关参数设置###########
###########施加激发自旋波的外加磁场###########
#激发自旋波的微波磁场的振幅,这里的单位为mT,表示2000 Oe
set Happ 200
#激发自旋波的微波磁场的频率,这里的单位为GHz
set frequency 4.1
#对初始的矢量场initialAntennaFiled进行变化,
#使其成为激发自旋波的外加磁场:H= Happ(xsinwt)
proc transformExcitationFiled { total_time } {
global frequency pi t0
set t $total_time
#计算w=2*pi*f,并把单位顺便转化为GHz
set w [expr {2 * $pi * $frequency * 1e9}]
set sinwt [expr {sin($w * $t)}]
set coswt [expr {cos($w * $t)}]
#计算x方向的磁场分量及其对时间的导数,其他方向为0
#即x方向H*sinwt
set Hx $sinwt
set dHx [expr {$w * $coswt}]
#返回6个元素的列表,即变换矩阵的3个主对角元素及其3个导数
return [list $Hx 0 0 $dHx 0 0]
}
#指定天线区域的矢量场(后面转化为磁场):H= (Happ 0 0),其他区域H=(0 0 0)
proc initialAntennaFiled { x y z } {
global nanowire_left Happ
#天线距离纳米线左端200nm,天线宽度为4nm
if {$x >= $nanowire_left + 200e-9 && $x <= $nanowire_left + 200e-9 + 4e-9} {
return "$Happ 0 0"
}
#其他区域无外加磁场
return "0 0 0"
}
#使用脚本指定天线区域的矢量场
Specify Oxs_ScriptVectorField:antennaFiled {
script initialAntennaFiled
script_args rawpt
atlas :atlas
}
#使用此类可生成任意(局域,时变)的外加磁场
Specify Oxs_TransformZeeman [subst {
field :antennaFiled
comment "函数返回6个元素,是3个主对角元素及其3个导数"
type diagonal
script transformExcitationFiled
script_args total_time
comment "将默认单位A/m换算为mT"
multiplier [expr {0.001/$mu0}]
comment "将stage_count设为0(默认值),让模拟的所有阶段都存在该塞曼能"
stage_count 0
}]
##########施加激发自旋波的外加磁场###########
#每个阶段固定为0.5ns,模拟总共运行6ns,应该生成12个磁化文件
Destination Record mmArchive
Schedule Oxs_TimeDriver::Magnetization Record stage 1
对于电流密度J=0的情况,这里选取模拟时间为第1.5ns时保存的磁化文件进行分析,使用命令行工具avf2odt提取沿着neel畴壁波导传播的自旋波,计算衰减长度。
使用的命令如下:
tclsh oommf.tcl avf2odt //主命令
-average point //取每个单元格的值
-region - 0 - - 1e-9 - //指定取样区域范围,-表示文件的默认范围,
-filesort "-ascii -increasing" //输入文件列表按照顺序增加来输入
-ipat TODO_picture\矢量图处理\sin磁场激发,自旋波衰减长度\待转换的磁化矢量文件\*.omf //输入文件所在的目录
-onefile TODO_picture\矢量图处理\sin磁场激发,自旋波衰减长度\磁化文件转odt文件\DW_M.odt //输出的odt文件名称
将输出的DW_M.odt数据表文件用mmGraph显示出来,如下所示:

注意 ,在磁体系的两端200nm的范围内都设置了高阻尼,用于吸收自旋波。可以大概看出从天线激发位置(x=-800nm)到振幅衰减到原来的1/e,所间隔的长度大概在900nm左右。但是和文章中L~1100nm还是差距巨大,我也不知道是哪里的问题?是模拟中所用的外加磁场不是sin函数?亦或是提取自旋波的空间范围错误?还是计算自旋波的衰减长度的方式错了?
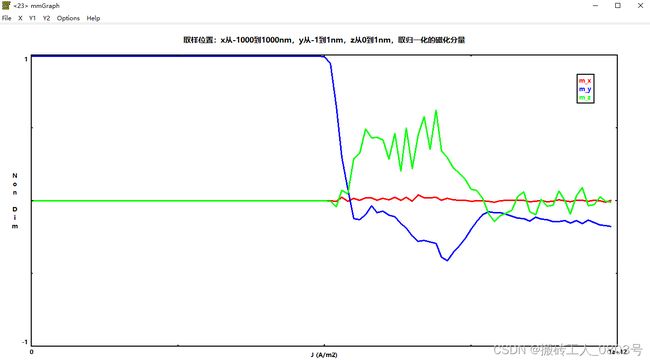
对于电流密度J=1e10A/m2的情况,选取模拟时间为第3.5ns时保存的磁化文件进行分析,将第5.5ns时的磁化文件作为J=2e10的情况。处理方式和上面一样,这里就不一个个放图了,直接同时显示这三个.odt文件如下(可惜mmGraph不支持按文件使用不同颜色绘制):
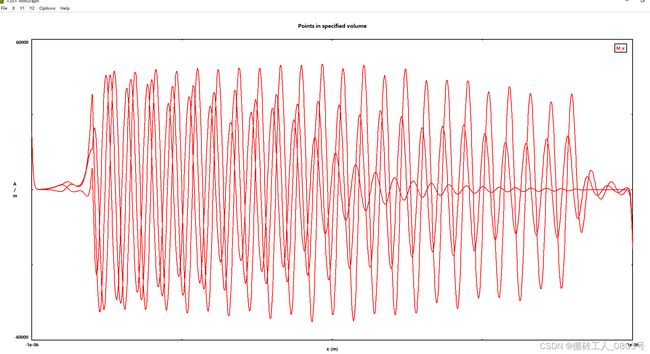
可以直观的看到,正的电流密度确实放大了自旋波,但是问题来了,怎么从图中得到正电流密度下的衰减长度呢?
对于电流密度J为负的情况,选取模拟时间为第1.5ns时当做J=-1e10A/m2的情况,第3.5ns时当做J=-2e10A/m2的情况,那么提取之后,直接同时显示这两个.odt文件如下:

看到结果直接傻眼了,J=-2e10的振幅比J=-1e10还要大,为什么没有抑制自旋波的振幅呢?
其余组也是差不多的情况,比如第五大组12GHz,J=0,1e10,2e10时看起来还算正常:
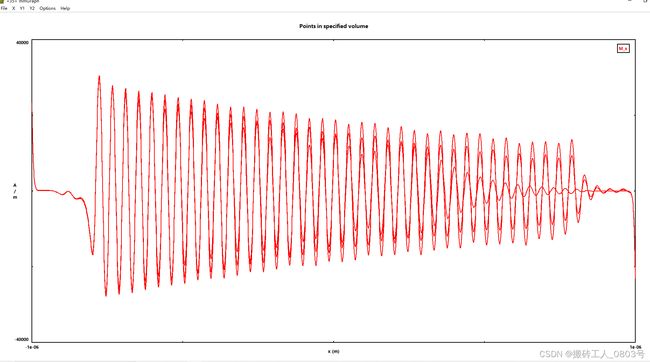
但是J=-1e10,-2e10时又不正常了:

6.FIG.5
当忽略SOT的类场项作用时,在不同电流密度作用下,对激发的自旋波进行二维FFT(即色散分析)。这里用于激发自旋波的外加磁场和FIG.2 (a)相同,也是使用sinc函数激发,为什么呢?因为参考MFA的示例程序,发现都是采用sinc函数来激发自旋波,然后对激发的自旋波进行一维FFT和二维FFT。按照电流密度的不同,共分为五组模拟:
第一组模拟:J=-2e10A/m2,eps_prime=0。
第二组模拟:J=-1e10A/m2,eps_prime=0。
第三组模拟:J=0,eps_prime=0。
第四组模拟:J=1e10A/m2,eps_prime=0。
第五组模拟:J=2e10A/m2,eps_prime=0。
显然,这里的第三、四组模拟,对应Figure S1中的第一、二组,故这里只需对第一、二、五组进行模拟,最后利用MFA对模拟结束后得到的磁化文件进行色散分析。
第三组模拟J=0,采用固定时间步长,模拟时间10ns的色散关系:
上面两张图差异很小,说明可能真的如上文3.Figure S1所说的那样与演化器的时间步长设置没关系,但是对比FIG.5的横坐标大于0的右半边图形,除了MFA生成的横坐标不同外(FIG.5的横坐标是Inverse wavelength,我不太确定这个英文表达的是波长的倒数,还是波矢(2pi/波长)),如果只看曲线变化趋势,似乎好像是相同的:都是有f1,f2两条曲线,f1的临界频率接近0,f2的临界频率接近60GHz。
接下来的四组模拟得到的色散关系都没有明显的差异。对于第五组模拟J=2e10,色散关系如下:

对于第四组模拟J=1e10,色散关系如下:

对于第二组模拟J=-1e10,色散关系如下:
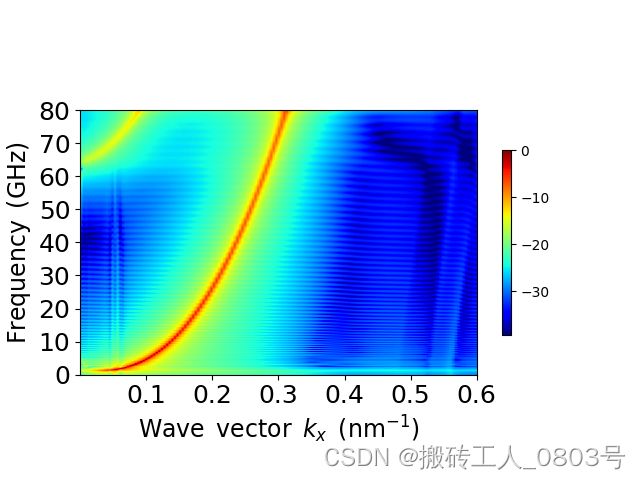
对于第一组模拟J=-2e10,色散关系如下:
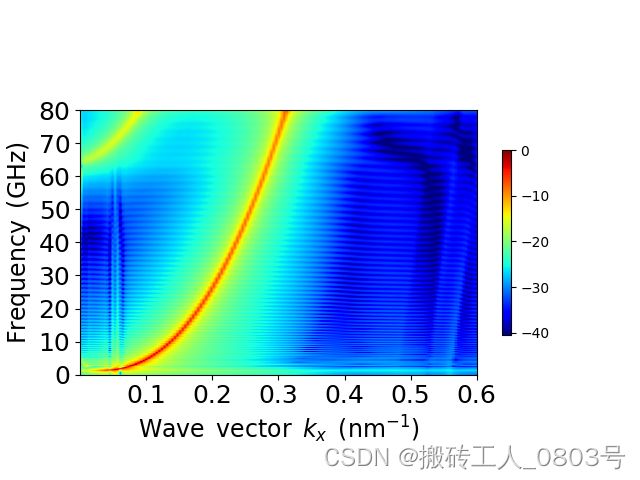
那么问题又来了,如何得到FIG.5的横坐标小于0的左半边图形呢?
总结
自己关于自旋波的理论知识还十分欠缺,微磁数据后处理的工具也了解不多。总之这个月差不多就是模拟错误的代码,利用错误的数据处理工具,遵循错误的方法来瞎搞。
同声自相应,同心自相知。----傅玄《何当行》