opencv霍夫线圆检测理解
霍夫变换-线圆检测
假设笛卡尔坐标系中有n个点,每个点坐标为 ( x i , y i ) (x_i, y_i) (xi,yi),且这些点大致拟合成一条直线,问:如何找到这条直线?
霍夫空间
对于每个点 ( x i , y i ) (x_i, y_i) (xi,yi) 都有无数条直线 y i = k x i + b y_i=kx_i+b yi=kxi+b 过该点。由k和b唯一确定该条直线,若将 ( k , b ) (k,b) (k,b) 看作一个坐标,则该坐标点即为霍夫空间下的坐标。霍夫空间可以看作是原函数的 参数空间。
同理,对于过某一点的圆的方程 ( x i − a ) 2 + ( y i − b ) 2 = r 2 (x_i-a)^2+(y_i-b)^2=r^2 (xi−a)2+(yi−b)2=r2 其参数构成的点 ( a , b , r ) (a,b,r) (a,b,r) 就是霍夫空间下的坐标。
有时,为了便于计算,会将笛卡尔坐标系转换为极坐标系进而得到极坐标系下的参数空间。
直线检测
在霍夫空间中 ( k , b ) (k,b) (k,b) 方程可以表示为 b = − x i k + y i b=-x_ik+y_i b=−xik+yi 也是一条直线。将所有n个点代入即可得到霍夫空间中的n条直线,若其中有m条直线相交于一点 ( k m , b m ) (k_m, b_m) (km,bm),对于这m条霍夫空间下的直线所对应的笛卡尔坐标下的m个点来说,它们有共同的k和b,即它们在同一条直线上,即检测出一条直线。对霍夫空间中所有直线的交点进行遍历就检测出所有的直线。进一步可以使用一些淘汰算法进行筛选及合并,减少多余的直线
圆检测
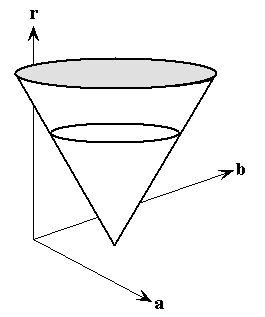
同直线检测,只不过将二维坐标系转换为三维。对于任意a、b,总能找到一个r,使得这三个参数构成的圆的方程过点 ( x i , y i ) (x_i,y_i) (xi,yi)。 ( a , b , r ) (a,b,r) (a,b,r) 在霍夫空间中的图形如下:
三个锥面相交即确定一个参数坐标点,进而得出经过这三点的圆的方程。
对 HoughCircles 方法中参数dp的理解
该参数可以理解为拟合精度,或者去除多余圆的程度。
简单理解为将霍夫空间的一个面(或一个空间等)划分为多个小格子,处于同一个格子的点视为一个点。dp即为每个小格子的宽度。dp=1 代表每个小格子仅代表一像素,即不进行合并。
例如,在霍夫空间下,有3个锥形,其中两个相交,第三个并没有过这个相交线,但该线与第三个锥面的最近距离小于2。此时,如果设置 dp=1 就检测不出圆形,因为并没有相交点。但如果设置 dp=2 则意味着所有小于2的距离将视为同一个点,此时就能检测出一个圆。
参考 我有点酷