图神经网络中的谱图理论基础
一、图的拉普拉斯矩阵
- 拉普拉斯算子
拉普拉斯算子(Laplace Operator)是为欧几里德空间中的一个二阶微分算子,定义为梯度的散度,可以写作 Δ , ∇ 2 , ∇ ⋅ ∇ \Delta ,\nabla ^{2},\nabla \cdot \nabla Δ,∇2,∇⋅∇这几种形式。如果函数 f f f是二阶可微的实函数,则 f f f的拉普拉斯算子可以写作:
Δ f = ∇ 2 f = ∇ ⋅ ∇ f \Delta f=\nabla ^{2}f=\nabla \cdot \nabla f Δf=∇2f=∇⋅∇f
这里简单介绍一下散度的概念:散度(divergence)用于表征空间各点矢量场发散的强弱程度。散度描述的是向量场里一个点是汇聚点还是发源点。值为正时表示该点为发源点,值为负时表示该点为汇聚点,值为零时表示该点无源。散度在物理上的含义可以理解为磁场、热源等。在笛卡尔坐标系中,矢量 V V V的散度表示为:
∇ ⋅ V = ∂ V x ∂ x + ∂ V y ∂ y + ∂ V z ∂ z \nabla \cdot V=\frac{\partial V_{x}}{\partial x}+\frac{\partial V_{y}}{\partial y}+\frac{\partial V_{z}}{\partial z} ∇⋅V=∂x∂Vx+∂y∂Vy+∂z∂Vz
那么拉普拉斯算子作为梯度的散度,则在笛卡尔坐标系中定义为:
Δ f = ∑ i = 1 n ∂ 2 f ∂ x i 2 \Delta f=\sum_{i=1}^{n}\frac{\partial ^{2}f}{\partial x_{i}^{2}} Δf=i=1∑n∂xi2∂2f
也就是表示为函数 f f f在各个维度上的二阶偏导数的和。
接下来来看一下拉普拉斯算子直观上表示什么含义,以一维空间为例:
Δ f ( x ) = ∂ 2 f ∂ x 2 = f ′ ′ ( x ) ≈ f ′ ( x ) − f ′ ( x − 1 ) ≈ [ f ( x + 1 ) − f ( x ) ] − [ f ( x ) − f ( x − 1 ) ] = f ( x + 1 ) + f ( x − 1 ) − 2 f ( x ) \Delta f(x)=\frac{\partial ^{2}f}{\partial x^{2}}\\ =f^{''}(x)\\ \approx f^{'}(x)-f^{'}(x-1)\\ \approx [f(x+1)-f(x)]-[f(x)-f(x-1)]\\ =f(x+1)+f(x-1)-2f(x) Δf(x)=∂x2∂2f=f′′(x)≈f′(x)−f′(x−1)≈[f(x+1)−f(x)]−[f(x)−f(x−1)]=f(x+1)+f(x−1)−2f(x)
也就是说二阶导数近似于二阶差分,从这一角度来看拉普拉斯算子直观上表示函数 f f f在当前点 x x x的所有自由度上进行微小扰动后所获得的函数值的增益,这里有 2 2 2个自由度,方向是 x x x的 + 1 +1 +1和 − 1 -1 −1方向。
接着来看二维空间的例子:
Δ f ( x , y ) = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 ≈ [ f ( x + 1 , y ) + f ( x − 1 , y ) − 2 f ( x , y ) ] + [ f ( x , y + 1 ) + f ( x , y − 1 ) − 2 f ( x , y ) ] = f ( x + 1 , y ) + f ( x − 1 , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) − 4 f ( x , y ) \Delta f(x,y)=\frac{\partial ^{2}f}{\partial x^{2}}+\frac{\partial ^{2}f}{\partial y^{2}}\\ \approx [f(x+1,y)+f(x-1,y)-2f(x,y)]+[f(x,y+1)+f(x,y-1)-2f(x,y)]\\ =f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y) Δf(x,y)=∂x2∂2f+∂y2∂2f≈[f(x+1,y)+f(x−1,y)−2f(x,y)]+[f(x,y+1)+f(x,y−1)−2f(x,y)]=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y)
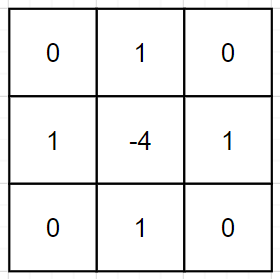
二维空间中的拉普拉斯算子表征一个点 x x x在 4 4 4个自由度上微扰以后的函数增益,方向分别为 ( 1 , 0 ) , ( − 1 , 0 ) , ( 0 , 1 ) , ( 0 , − 1 ) (1,0),(-1,0),(0,1),(0,-1) (1,0),(−1,0),(0,1),(0,−1)。这就是图像中的拉普拉斯卷积核,如果算上对角线以后可以认为有 8 8 8个自由度:
那么我们可以认为:拉普拉斯算子是所有自由度上进行微小变化后所获得的增益。
- 图的表示
一个网络(无向图)由节点与节点之间的边组成。每个节点是有值的,我们用 f f f来表示节点的值:
f = ( f 1 f 2 ⋯ f N ) T f=\begin{pmatrix} f_{1} & f_{2} & \cdots & f_{N} \end{pmatrix}^{T} f=(f1f2⋯fN)T
这里的 f f f是一个向量, f i f_i fi表示网络中节点 i i i的值,也就是函数 f f f在节点 i i i处的值,类比 f ( x , y ) f(x,y) f(x,y)在 ( x , y ) (x,y) (x,y)处的值。
网络中除了节点还有边,每条边还有可能带有权重,我们用 W W W表示网络的加权邻接矩阵, W N × N = [ w i j ] , 1 ≤ i , j ≤ N W_{N\times N}=[w_{ij}],1\leq i,j\leq N WN×N=[wij],1≤i,j≤N,其中 w i j w_{ij} wij表示节点 i i i和节点 j j j的边的权重,另有 W W W是一个对称矩阵,有 w i j = w j i w_{ij}=w_{ji} wij=wji。
另外还有度的概念,这里可以类比有向图中的出度和入度的概念,不过图中的点 v i v_i vi的度 d i d_i di并不是和该点相连的点的数量,而是和其相连的边的权重之和,也就是邻接矩阵的每一行的值加起来,即:
d i = ∑ j = 1 N w i j d_{i}=\sum_{j=1}^{N}w_{ij} di=j=1∑Nwij
而图的度矩阵(对角矩阵) D N × N D_{N\times N} DN×N可以表示如下:
D = [ d 1 d 2 d N ] D=\begin{bmatrix} d_{1} & & & \\ & d_{2} & & \\ & & & \\ & & & d_{N} \end{bmatrix} D=⎣⎢⎢⎡d1d2dN⎦⎥⎥⎤
- 图的拉普拉斯矩阵
可以将拉普拉斯算子推广到网络(无向图)中,对于有 N N N个节点的网络,我们想要获得一个节点关于其邻居节点(自由度)的增益,然而每个节点的邻居个数不一定是相同的,一个节点的最大自由度为 N N N。
在网络中,两个节点之间的增益为 f i − f j f_{i}-f_{j} fi−fj,考虑进边的权重,增益就为 w i j ( f i − f j ) w_{ij}(f_{i}-f_{j}) wij(fi−fj)。对于节点 i i i来说,它从它的邻居节点所获得的总增益就是拉普拉斯算子在节点 i i i处的值:
Δ f i = ∑ j ∈ N B ( i ) ∂ f i ∂ j 2 = ∑ j w i j ( f i − f j ) = ( ∑ j w i j ) f i − ∑ j w i j f j = d i f i − w i : f \Delta f_{i}=\sum_{j\in NB(i)}\frac{\partial f_{i}}{\partial j^{2}}\\ =\sum_{j}w_{ij}(f_{i}-f_{j})\\ =(\sum _{j}w_{ij})f_{i}-\sum_{j}w_{ij}f_{j}\\ =d_{i}f_{i}-w_{i:}f Δfi=j∈NB(i)∑∂j2∂fi=j∑wij(fi−fj)=(j∑wij)fi−j∑wijfj=difi−wi:f
这里公式第二行 j j j从 j ∈ N B ( i ) j\in NB(i) j∈NB(i)推广到所有的 j j j是因为 w i j w_{ij} wij可以控制节点 i i i的邻居节点(这是因为不相邻的边的权重 w i j = 0 w_{ij}=0 wij=0)。另外注意这里计算 f i f_i fi处的总增益,式子中却是 f i − f j f_i-f_j fi−fj,而不是 f j − f i f_j-f_i fj−fi,这样其实是没有关系的。
那么拉普拉斯算子在所有的节点上的作用结果就是:
Δ f = ( Δ f 1 Δ f 2 ⋮ Δ f N ) = ( d 1 f 1 − w 1 : f d 2 f 2 − w 2 : f ⋮ d N f N − w N : f ) = ( d 1 d 2 ⋱ d N ) f − ( w 1 : w 2 : ⋮ w N : ) f = ( D − W ) f \Delta f=\begin{pmatrix} \Delta f_{1}\\ \Delta f_{2}\\ \vdots \\ \Delta f_{N} \end{pmatrix}\\ =\begin{pmatrix} d_{1}f_{1}-w_{1:}f\\ d_{2}f_{2}-w_{2:}f\\ \vdots \\ d_{N}f_{N}-w_{N:}f \end{pmatrix}\\ =\begin{pmatrix} d_{1} & & & \\ & d_{2} & & \\ & & \ddots & \\ & & & d_{N} \end{pmatrix}f-\begin{pmatrix} w_{1:}\\ w_{2:}\\ \vdots \\ w_{N:} \end{pmatrix}f\\ =(D-W)f Δf=⎝⎜⎜⎜⎛Δf1Δf2⋮ΔfN⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛d1f1−w1:fd2f2−w2:f⋮dNfN−wN:f⎠⎟⎟⎟⎞=⎝⎜⎜⎛d1d2⋱dN⎠⎟⎟⎞f−⎝⎜⎜⎜⎛w1:w2:⋮wN:⎠⎟⎟⎟⎞f=(D−W)f
这里的 D − W D-W D−W就是图的拉普拉斯矩阵(Graph Laplacian),记作 L L L。根据上面的公式,我们得出结论:图拉普拉斯算子作用在由图节点信息构成的向量 f f f上得到的结果等于图拉普拉斯矩阵和向量 f f f的点积。拉普拉斯矩阵反映了当前节点对周围节点产生扰动时所产生的累积增益,直观上也可以理解为某一节点的值变为其相邻节点值的期望影响。
- 拉普拉斯矩阵的谱分解
拉普拉斯矩阵的谱分解(Laplace Spectral Decomposition)就是拉普拉斯矩阵的特征分解:
L μ k = λ k μ k L\mu _{k}=\lambda _{k}\mu _{k} Lμk=λkμk
对于无向图来说,拉普拉斯矩阵是实对称矩阵,而实对称矩阵一定可以用正交矩阵进行正交相似对角化:
L = U Λ U − 1 L=U\Lambda U^{-1} L=UΛU−1
这里的 Λ \Lambda Λ为特征值构成的对角矩阵, U U U为特征向量构成的正交矩阵, U U U的每一列都是一个特征向量。又因为正交矩阵的逆等于正交矩阵的转置: U − 1 = U T U^{-1}=U^{T} U−1=UT,所以有:
L = U Λ U − 1 = U Λ U T L=U\Lambda U^{-1}=U\Lambda U^{T} L=UΛU−1=UΛUT
- 拉普拉斯矩阵的性质
拉普拉斯矩阵有一些性质如下:
①对称性。
②由于其对称性,则它的所有特征值都是实数。
③对于任意向量 f f f,有:
f T L f = 1 2 ∑ i = 1 N ∑ j = 1 N w i j ( f i − f j ) 2 f^{T}Lf=\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}w_{ij}(f_{i}-f_{j})^{2} fTLf=21i=1∑Nj=1∑Nwij(fi−fj)2
这一性质利用拉普拉斯矩阵的性质很容易可以得到:
f T L f = f T D f − f T W f = ∑ i = 1 N d i f i 2 − ∑ i = 1 N ∑ j = 1 N w i j f i f j = 1 2 ( ∑ i = 1 N d i f i 2 − 2 ∑ i = 1 N ∑ j = 1 N w i j f i f j + ∑ j = 1 N d j f j 2 ) = 1 2 ( ∑ i = 1 N ∑ j = 1 N w i j f i 2 − 2 ∑ i = 1 N ∑ j = 1 N w i j f i f j + ∑ i = 1 N ∑ j = 1 N w i j f j 2 ) = 1 2 ∑ i = 1 N ∑ j = 1 N w i j ( f i − f j ) 2 f^{T}Lf=f^{T}Df-f^{T}Wf \\ =\sum _{i=1}^{N}d_{i}f_{i}^{2}-\sum_{i=1}^{N}\sum_{j=1}^{N}w_{ij}f_{i}f_{j}\\ =\frac{1}{2}(\sum _{i=1}^{N}d_{i}f_{i}^{2}-2\sum_{i=1}^{N}\sum_{j=1}^{N}w_{ij}f_{i}f_{j}+\sum _{j=1}^{N}d_{j}f_{j}^{2})\\ =\frac{1}{2}(\sum_{i=1}^{N}\sum_{j=1}^{N}w_{ij}f_{i}^{2}-2\sum_{i=1}^{N}\sum_{j=1}^{N}w_{ij}f_{i}f_{j}+\sum_{i=1}^{N}\sum_{j=1}^{N}w_{ij}f_{j}^{2})\\ =\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}w_{ij}(f_{i}-f_{j})^{2} fTLf=fTDf−fTWf=i=1∑Ndifi2−i=1∑Nj=1∑Nwijfifj=21(i=1∑Ndifi2−2i=1∑Nj=1∑Nwijfifj+j=1∑Ndjfj2)=21(i=1∑Nj=1∑Nwijfi2−2i=1∑Nj=1∑Nwijfifj+i=1∑Nj=1∑Nwijfj2)=21i=1∑Nj=1∑Nwij(fi−fj)2
④拉普拉斯矩阵是半正定的,则其所有特征值非负,这个性质由性质③很容易得出。并且其最小的特征值为 0 0 0,这是因为 L L L的每一行和为 0 0 0,对于标准化的全 1 1 1向量 1 N = ( 1 1 ⋯ 1 ) T / N 1_{N}=\begin{pmatrix} 1 & 1 & \cdots & 1 \end{pmatrix}^{T}/\sqrt{N} 1N=(11⋯1)T/N,有 L ⋅ 1 N = 0 = 0 ⋅ 1 N L\cdot 1_{N}=0=0\cdot 1_{N} L⋅1N=0=0⋅1N。
对于上面的性质③,如果 f f f为网络中信号的值的向量,那么 f T L f f^{T}Lf fTLf称为图信号的总变差(Total Variation),可以刻画图信号整体的平滑度(Smoothness)。
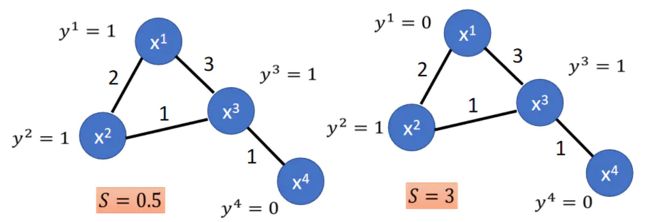
那么为什么 f T L f f^{T}Lf fTLf可以刻画图的平滑度呢?这里我们可以直观地来看一下,从③的式子中可以看出如果相邻节点的值 f i f_i fi和 f j f_j fj差异很大,那么 f T L f f^{T}Lf fTLf这个值就会很大,也就会不平滑。举例来说, f i f_i fi可以看做节点 x i x_i xi的标签 y i y_i yi,这里将 f T L f f^{T}Lf fTLf记作 S S S。如果一个图比较平滑的话,那么图中相邻节点的标签应该是尽可能一致的,如果相邻节点的标签差异很大,那么这个图就不是很平滑。如下图:
上图中的两个网络,第一个网络的节点标签差异较小(更平滑),因此 S S S较小,而第二个网络节点标签差异较大(不平滑),因此 S S S较大。因此 S = f T L f S=f^{T}Lf S=fTLf可以用来刻画网络的平滑度(越小越平滑)。
多说一句,这一点可以用在半监督学习中,大概的思路是构建有标签和无标签数据的无向图,节点就是每一个数据样本,边是节点间的相似度(使用径向基函数等来度量的相似度),为了使模型为无标签数据标注的标签更平滑,可以将 S S S作为训练模型的一个正则项。感兴趣的同学可以参考:半监督学习|深度学习(李宏毅)(九)。
图的拉普拉斯矩阵的应用是多种多样的,本文只介绍一些学习图神经网络(主要是图卷积网络GCN)的一些基础知识。图的拉普拉斯矩阵还可以应用在谱聚类方法中,这是一种聚类方法,也可当做一种降维方法,感兴趣的同学可以参考:谱聚类|机器学习推导系列(二十)。
二、图傅里叶变换
本章节需要了解傅里叶变换的相关知识,可以参考这篇文章:傅里叶级数与傅里叶变换。
- 回顾傅里叶变换
对于连续非周期函数 f ( t ) f(t) f(t)的傅里叶变换,其公式为:
F ( ω ) = ∫ − ∞ + ∞ f ( t ) e − i ω t d t F(\omega )=\int_{-\infty }^{+\infty }f(t)e^{-i\omega t}\mathrm{d}t F(ω)=∫−∞+∞f(t)e−iωtdt
傅里叶变换将函数分解成无数个基函数的线性组合,向每个基函数 e − i ω t e^{-i\omega t} e−iωt上投影, F ( ω ) F(\omega ) F(ω)就是投影后对应的该基函数的系数。定义在 ( − ∞ , + ∞ ) (-\infty ,+\infty ) (−∞,+∞)上的函数 f ( t ) f(t) f(t)可以看做一个无限维的向量,而 t t t代表的就是维度, f ( t ) f(t) f(t)就是这个维度上的值,因此函数的内积也就是积分。 e − i ω t e^{-i\omega t} e−iωt是傅里叶变换的基函数,而 w ∈ ( − ∞ , + ∞ ) w\in (-\infty ,+\infty ) w∈(−∞,+∞),也就是说有无限多个基函数, F ( ω ) F(\omega ) F(ω)表示函数 f ( t ) f(t) f(t)在这个基函数上的坐标。
- 亥姆霍兹方程与傅里叶变换
亥姆霍兹方程的公式为:
∇ 2 f = − k 2 f \nabla ^{2}f=-k^{2}f ∇2f=−k2f
亥姆霍兹方程可以看做广义的特征函数 A x = λ x Ax=\lambda x Ax=λx, f f f为特征函数, − k 2 -k^{2} −k2为特征值(之前说过一个函数 f f f可以看做无限维的向量,这里也可以用这个观点来理解亥姆霍兹方程)。
现在我们让拉普拉斯算子 ∇ 2 \nabla ^{2} ∇2作用到傅里叶变换的基函数上,则有:
∇ 2 e − i ω t = ∂ 2 e − i ω t ∂ t 2 = − ω 2 e − i ω t \nabla ^{2}e^{-i\omega t}=\frac{\partial ^{2}e^{-i\omega t}}{\partial t^{2}}=-\omega ^{2}e^{-i\omega t} ∇2e−iωt=∂t2∂2e−iωt=−ω2e−iωt
因此我们可以看出,傅里叶变换的基函数其实就是拉普拉斯算子的特征函数,而 ω \omega ω就代表了拉普拉斯算子的特征值。
- 从傅里叶变换到图傅里叶变换
对于傅里叶变换,存在卷积定理:在适当条件下,两个信号的卷积的傅立叶变换是他们的傅立叶变换的点积,换句话说就是时域卷积等于频域相乘。为了能够应用卷积定理来处理卷积,所以可以将两个信号 f f f和 g g g首先进行傅里叶变换再相乘,从而得到卷积结果,这样做的好处在于可以降低算法的时间复杂度。用公式表达卷积定理就是:
F ( f ∗ g ) = F ( f ) ⋅ F ( g ) F(f*g)=F(f)\cdot F(g) F(f∗g)=F(f)⋅F(g)
对于网络来说,直接进行卷积是困难的,因为网络不具备图像那样规则的网格结构,因此考虑应用图傅里叶变换将网络的空域信息映射到频域来应用卷积定理完成卷积操作。
图傅里叶变换是使用类比的方式直接定义的,并非经过严格推导,类比的方法如下:
①拉普拉斯算子与拉普拉斯矩阵:拉普拉斯算子的作用是能够得到一个点在某些自由度上微扰以后获得的增益,而拉普拉斯矩阵能够获得网络中的每个节点微扰以后从它的邻居节点上获得的增益,也就是说:拉普拉斯矩阵之于网络就相当于拉普拉斯算子之于函数。
②拉普拉斯算子的特征函数与拉普拉斯矩阵的特征向量:傅里叶变换的基函数 e − i ω t e^{-i\omega t} e−iωt是拉普拉斯算子的特征函数,那么同样的图傅里叶变换的基向量就是拉普拉斯矩阵的特征向量 μ k \mu _{k} μk。
③拉普拉斯算子的特征值与拉普拉斯矩阵的特征值:傅里叶变换的频率 ω \omega ω是拉普拉斯算子的特征值,那么同样的图傅里叶变换的频率就是拉普拉斯矩阵的特征值 λ k \lambda _{k} λk。
总而言之,这个类比的过程如下:
∇ 2 e − i ω t = − ω 2 e − i ω t ⇕ L μ k = λ k μ k {\color{Red}{\nabla ^{2}}}{\color{Blue}{e^{-i\omega t}}}={\color{Green}{-\omega ^{2}}}{\color{Blue}{e^{-i\omega t}}}\\ \Updownarrow \\ {\color{Red}{L}}{\color{Blue}{\mu _{k}}}={\color{Green}{\lambda _{k}}}{\color{Blue}{\mu _{k}}} ∇2e−iωt=−ω2e−iωt⇕Lμk=λkμk
既然对于函数来说拉普拉斯算子的特征值和特征函数能够用于函数的傅里叶变换,那么对于网络来说拉普拉斯矩阵的特征值和特征向量就能够用于网络的傅里叶变换。换句话说,傅里叶变换是以拉普拉斯算子的特征函数为基进行投影,那么图傅里叶变换就以拉普拉斯矩阵的特征向量为基进行投影,因此图傅里叶变换定义为:
F ( λ k ) = ∑ i = 1 N f ( i ) μ k ( i ) F(\lambda _{k})=\sum_{i=1}^{N}f(i)\mu _{k}(i) F(λk)=i=1∑Nf(i)μk(i)
这里的 f f f还是表示由图节点信息构成的向量, λ k \lambda _{k} λk和 μ k \mu _{k} μk分别表示拉普拉斯矩阵的特征值和特征向量。现在我们用 f ^ \hat{f} f^来表示 f f f经过图傅里叶变换后的坐标,那么图傅里叶变换可以表示成矩阵形式:
f ^ = ( f ^ 1 ⋮ f ^ N ) = ( μ 1 ( 1 ) ⋯ μ 1 ( N ) ⋮ ⋱ ⋮ μ N ( 1 ) ⋯ μ N ( N ) ) ( f 1 ⋮ f N ) = U T f \hat{f}=\begin{pmatrix} \hat{f}_{1}\\ \vdots \\ \hat{f}_{N} \end{pmatrix}=\begin{pmatrix} \mu _{1}(1) & \cdots & \mu _{1}(N)\\ \vdots & \ddots & \vdots \\ \mu _{N}(1) & \cdots & \mu _{N}(N) \end{pmatrix}\begin{pmatrix} f_{1}\\ \vdots \\ f_{N} \end{pmatrix}=U^{T}f f^=⎝⎜⎛f^1⋮f^N⎠⎟⎞=⎝⎜⎛μ1(1)⋮μN(1)⋯⋱⋯μ1(N)⋮μN(N)⎠⎟⎞⎝⎜⎛f1⋮fN⎠⎟⎞=UTf
我们也可以得到图傅里叶变换的逆变换:
f = U U − 1 f = U U T f = U f ^ f=UU^{-1}f=UU^{T}f=U\hat{f} f=UU−1f=UUTf=Uf^
参考资料
ref:【GCN】万字长文带你入门 GCN——公众号:阿泽的学习笔记
ref:图傅里叶变换