卡方分布（Chi-Squared Distribution）

定义

通俗的说就是通过小数量的样本容量去预估总体容量的分布情况

卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度

若n个相互独立的随机变量ξ₁，ξ₂，...,ξn ，均服从标准正态分布（也称独立同分布于标准正态分布），则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量，其分布规律称为卡方分布（chi-square distribution）

卡方检验的基本思想是根据样本数据推断总体的频次与期望频次是否有显著性差异

 公式：

                    

 where  Γ()=(−1)! and   denotes the degrees of freedom.

 

# IMPORTS
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import matplotlib.style as style
from IPython.core.display import HTML

# PLOTTING CONFIG
%matplotlib inline
style.use('fivethirtyeight')
plt.rcParams["figure.figsize"] = (14, 7)

plt.figure(dpi=100)

# PDF
plt.plot(np.linspace(0, 20, 100), 
         stats.chi2.pdf(np.linspace(0, 20, 100), df=4) ,
        )
plt.fill_between(np.linspace(0, 20, 100),
                 stats.chi2.pdf(np.linspace(0, 20, 100), df=4) ,
                 alpha=.15,
                )

# CDF
plt.plot(np.linspace(0, 20, 100), 
         stats.chi2.cdf(np.linspace(0, 20, 100), df=4),
        )

# LEGEND
plt.xticks(np.arange(0, 21, 2))
plt.text(x=11, y=.25, s="pdf (normed)", alpha=.75, weight="bold", color="#008fd5")
plt.text(x=11, y=.85, s="cdf", alpha=.75, weight="bold", color="#fc4f30")

# TICKS
plt.xticks(np.arange(0, 21, 2))
plt.tick_params(axis = 'both', which = 'major', labelsize = 18)
plt.axhline(y = 0, color = 'black', linewidth = 1.3, alpha = .7)

# TITLE, SUBTITLE & FOOTER
plt.text(x = -2, y = 1.25, s = r"Chi-Squared $(\chi^{2})$ Distribution - Overview",
               fontsize = 26, weight = 'bold', alpha = .75)
plt.text(x = -2, y = 1.1, 
         s = 'Depicted below are the normed probability density function (pdf) and the cumulative density\nfunction (cdf) of a Chi-Squared distributed random variable $ y \sim \chi^{2}(k) $, given $k$=4.',
         fontsize = 19, alpha = .85)

 改变自由度k的值，不同自由度如下所示：
 

plt.figure(dpi=100)

# PDF k = 1
plt.plot(np.linspace(0, 15, 500), 
         stats.chi2.pdf(np.linspace(0, 15, 500), df=1),
        )
plt.fill_between(np.linspace(0, 15, 500),
                 stats.chi2.pdf(np.linspace(0, 15, 500), df=1),
                 alpha=.15,
                )

# PDF k = 3
plt.plot(np.linspace(0, 15, 100), 
         stats.chi2.pdf(np.linspace(0, 15, 100), df=3),
        )
plt.fill_between(np.linspace(0, 15, 100),
                 stats.chi2.pdf(np.linspace(0, 15, 100), df=3),
                 alpha=.15,
                )

# PDF k = 6
plt.plot(np.linspace(0, 15, 100), 
         stats.chi2.pdf(np.linspace(0, 15, 100), df=6),
        )
plt.fill_between(np.linspace(0, 15, 100),
                 stats.chi2.pdf(np.linspace(0, 15, 100), df=6),
                 alpha=.15,
                )

# LEGEND
plt.text(x=.5, y=.7, s="$ k = 1$", rotation=-65, alpha=.75, weight="bold", color="#008fd5")
plt.text(x=1.5, y=.35, s="$ k = 3$", alpha=.75, weight="bold", color="#fc4f30")
plt.text(x=5, y=.2, s="$ k = 6$", alpha=.75, weight="bold", color="#e5ae38")


# TICKS
plt.tick_params(axis = 'both', which = 'major', labelsize = 18)
plt.axhline(y = 0, color = 'black', linewidth = 1.3, alpha = .7)

# TITLE, SUBTITLE & FOOTER
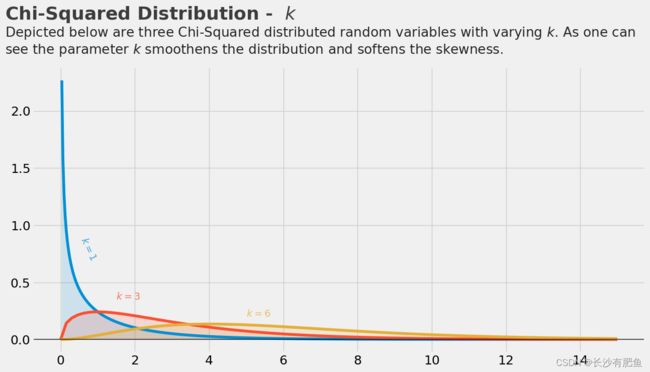
plt.text(x = -1.5, y = 2.8, s = "Chi-Squared Distribution - $ k $",
               fontsize = 26, weight = 'bold', alpha = .75)
plt.text(x = -1.5, y = 2.5, 
         s = 'Depicted below are three Chi-Squared distributed random variables with varying $ k $. As one can\nsee the parameter $k$ smoothens the distribution and softens the skewness.',
         fontsize = 19, alpha = .85)

 构造随机的卡方分布：

import numpy as np
from scipy.stats import chi2

# draw a single sample
np.random.seed(42)
print(chi2.rvs(df=4), end="\n\n")

# draw 10 samples
print(chi2.rvs(df=4, size=10), end="\n\n")

4.787358779738473

[2.98892946 2.76456717 2.76460459 9.29942882 5.73341246 2.262156
 4.93962895 3.99792053 0.43182989 1.34248457]

 质量密度函数：

from scipy.stats import chi2

# additional imports for plotting purpose
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams["figure.figsize"] = (14,7)



# continuous pdf for the plot
x_s = np.arange(15)
y_s = chi2.pdf(x=x_s, df=4)
plt.scatter(x_s, y_s, s=100);

 累计质量密度函数：

from scipy.stats import chi2

# probability of x less or equal 0.3
print("P(X <=3) = {}".format(chi2.cdf(x=3, df=4)))

# probability of x in [-0.2, +0.2]
print("P(2 < X <= 8) = {}".format(chi2.cdf(x=8, df=4) - chi2.cdf(x=2, df=4)))

P(X <=3) = 0.4421745996289252
P(2 < X <= 8) = 0.6441806878992138