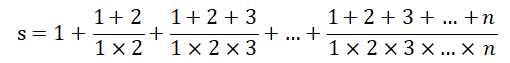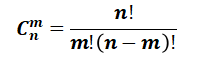Python语言程序设计实验(2)—— Python函数与类
实验1:公式计算
题目描述:
编写三个函数fz(n), fm(n), sum_(n)分别计算下列公式的分子和,分母积以及公式总和值。
提示:采用函数嵌套实现
def fz(n): #计算分子部分
s=0.0
for i in range(n):
s+=i+1
return s
def fm(n): #计算分母部分
s=1.0
for i in range(n):
s *=i+1
return s
def sum_(n): #计算公式的值
s=0.0
for i in range(n):
s+=fz(i+1)/fm(i+1)
return s
n=int(input("输入要计算的项数:"))
print(sum_(n))
实验2:阶乘计算
题目描述:
编写一个函数fac(n )求给定整数的阶乘,调用此函数实现以下公式。
提示:采用递归实现
def fac(n):
if n==1:
return 1;
else:
return fac(n-1)*n
def fac1(n):
s=1.0
for i in range(n):
s*=i+1
return s
n=int(input("输入要组合计算的下数:"))
m=int(input("输入要组合计算的上数:"))
print("递归方法一的结果:" + str(fac(n)/(fac(m)*fac(n-m))))
print("普通方法二的结果:" + str(fac1(n)/(fac1(m)*fac1(n-m))))
实验3:回文数判断
题目描述:
编写一个函数isHui(n),用以实现对正整数n判断是否是回文数。
提示:回文数定义:是指顺读与倒读数字相同的正整数。如12321。说明如下:
(1)求字符串长度函数len(s)
(2)当前位置为i,则其对称位置为j=len(s)-1-i
(3)切片方法取出字符判断是否相对:s[i:i+1]==s[j:j+1]
def isHui(s):
f=True
n=len(s)
for i in range(n):
j=n-1-i #j为i的对称位置
if s[i:i+1]!=s[j:j+1]: #当前位置i与对称位置j
f=False
break
return f
n=input("输入要组合计算的下数:")
if isHui(n):
print(n + "是回文数!")
else:
print(n + "不是回文数!")
实验4:找最长单词
题目描述:
编写一个函数maxWord(s),用以找出已知字符串s中的最长单词。
提示:输入“I am a student and my name is wpf!”,输出“student”。相关说明如下:
(1)查找空格函数i=s.find(’ '),通过while i>0循环查找
(2)取出当前单词:tempword=s[ :i]
(3)剔除单词,重新赋值句子:s=s[i+1:]
def maxWord(s):
maxword=''
tempword=''
n=len(s)
i=s.find(' ') #查找空格函数
s=s+' '
while i>0:
tempword=s[:i] #取出当前分割单词
if len(maxword)<len(tempword):
maxword=tempword
s=s[i+1:] #剔除判断后单词,重新修改句子
i=s.find(' ')
return maxword
s=input("输入英文句子:")
print(maxWord(s))
实验5:类的定义
题目描述:
定义一个dog类,包含name、age、weight等属性,设计一个构造函数对这些属性记性初始化,然后实现并测试这个类。
class dog:
name=''
age=0
weight=0
def __init__(self,n,a,w):
self.name=n
self.age=0
self.weight=0
def run():
print("go fast!")
def bark():
print("woof...!")
def eat():
print("yummy...!")
#案例测试
d1=dog("Tom",2,28)
dog.bark()
dog.run()
dog.eat()
实验6:类的单继承
题目描述:
定义一个 person基类,包含公有属性:姓名name、年龄age,具有speak()公有方法;从person类中派生出一个teacher子类,该类新增私有属性:专业profession、职称title、主讲课程course,并定义重写基类speak( )方法。
提示:实例测试
结果输出:
class person: #基类定义
name='' #姓名
age=0 #年龄
def __init__(self,n,a):#定义构造方法
self.name=n
self.age=a
def speak(self):#定义类本身的方法
print("my name is %s,I am %d years old."%(self.name,self.age))
class teacher(person): #派生类定义
__profession='' #专业
__title='' #职称
__course='' #主讲课程
def __init__(self,n,a,p,t,c): #定义子类的构造函数
person.__init__(self,n,a) #调用父类的构造函数
self.__profession=p
self.__title=t
self.__course=c
def speak(self): #重写父类的方法
print("my name is %s, I am %d years old,\nAnd my profession is %s,\nmy title is %s,\nmy master course is %s.\nthank you!"%(self.name,self.age,self.__profession,self.__title,self.__course))
#实例测试
s=teacher('wpf',42,'computer science and technology','associate professor','Python programming desiging')
s.speak()
实验7:类的多继承
题目描述:
定义一个student基类,包含公有属性:学号sid、班级class_,具有study()公有方法;再定义一个teacher基类,包含公有属性:工号tid、学院dept,具有teach()公有方法;然后从student和teacher两个基类公共派生出一个doctor子类,该类新增公有属性:姓名name、年龄age,具有introduce()公有方法,不需要重写两个基类方法。
提示:实例测试
结果输出:
class student: #基类1定义
sid='' #学号
class_='' #班级
def __init__(self,s,c):
self.sid=s
self.class_=c
def study(self):
print("My student's id is %s,\nI major in %s."%(self.sid,self.class_))
class teacher: #基类2定义
tid='' #工号
dept='' #院系
def __init__(self,t,d):
self.tid=t
self.dept=d
def teach(self):
print("And my teacher's id is %s,\nI am in %s."%(self.tid,self.dept))
class doctor(student,teacher): #派生类3多重继承
name=''
age=0
def __init__(self,s,c,t,d,n,a):
student.__init__(self,s,c) #基类1构造函数
teacher.__init__(self,t,d) #基类2构造函数
self.name=n
self.age=a
def introduce(self):
print("My name is %s, I am %d years old."%(self.name,self.age))
#实例测试
d1=doctor('2011038','Agricultural machinery engineering','2001020','college of imformatics','wpf',34)
d1.introduce()
d1.study()
d1.teach()
实验8:类的运算符重载
题目描述:
定义一个三维向量类Vector3,并定义相应的特殊方法实现两个该类对象之间的加、减运算(要求支持运算符+、-),实现该类对象与标量的乘、除运算(要求支持运算符*、/),以及向量长度的计算(要求使用属性实现,其中向量长度是向量所有分量平方和的平方根)。
提示:
通过类的专有方法__add__()、sub()、mul()、__truediv()分别实现+、-、*、/运算符重载;通过类的专有方法__str()查看向量,格式化显示向量坐标分量;通过自定义方法length(self)计算向量长度,并@property方法将向量长度设置为属性值。具体做法如下:
(1)定义向量构造方法:init(self, x, y, z),实现向量初始化Vector3(x, y, z)
(2)定义向量与另一个向量的加法+运算:add(self, anotherPoint)
(3)定义向量与另一个向量的加法-运算:sub(self, anotherPoint)
(4)定义向量与某一个标量的乘法*运算:mul(self, n)
(5)定义向量与某一个标量的除法/运算:truediv(self, n),注意:此处不是__div__
(6)定义向量查看方法:str(self),格式化显示向量坐标分量
(7)定义向量长度计算方法:length(self),实现向量所有分量平方和的平方根。
(8)实例测试:
结果输出:
class Vector3:
#构造方法,初始化,定义向量坐标
def __init__(self,x,y,z):
self.__x=x
self.__y=y
self.__z=z
#加上一个向量,对应分量相加,返回新向量
def __add__(self,anotherPoint):
x=self.__x + anotherPoint.__x
y=self.__y + anotherPoint.__y
z=self.__z + anotherPoint.__z
return Vector3(x,y,z)
#减去一个向量,对应分量相减,返回新向量
def __sub__(self,anotherPoint):
x=self.__x - anotherPoint.__x
y=self.__y - anotherPoint.__y
z=self.__z - anotherPoint.__z
return Vector3(x,y,z)
#向量与一个数字相乘,各分量乘以同一个数字,返回新向量
def __mul__(self,n):
x,y,z=self.__x*n, self.__y*n, self.__z*n
return Vector3(x,y,z)
#向量与一个数字相除,各分量除以同一个数字,返回新向量
def __truediv__(self,n):
x,y,z=self.__x/n, self.__y/n, self.__z/n
return Vector3(x,y,z)
#查看向量,格式化显示向量坐标分量
def __str__(self):
return "Vector3({},{},{})".format(self.__x,self.__y,self.__z)
#计算向量长度设置为属性,向量长度即所有分量平方和的平方根
@property
def length(self):
return (self.__x**2 + self.__y**2 + self.__z**2)**0.5
#实例测试
v1=Vector3(3,4,5)
v2=Vector3(5,6,7)
print(v1+v2)
print(v1-v2)
print(v1*3)
print(v2/2)
print(v1.length)